Quantitative ultrasound brain imaging with multiscale deconvolutional waveform inversion

Yu-Bing Li(李玉冰), Jian Wang(王建),†, Chang Su(苏畅),,3,‡,Wei-Jun Lin(林伟军),,3, Xiu-Ming Wang(王秀明),,3, and Yi Luo(骆毅)

1Institute of Acoustics,Chinese Academy of Sciences,Beijing 100190,China

2University of the Chinese Academy of Sciences,Beijing 100049,China

3Beijing Deep Sea Drilling Measurement Engineering Technology Research Center,Beijing 100190,China

Keywords: ultrasound brain imaging,full waveform inversion,high resolution,digital body

1. Introduction

Images of human brain at high spatial resolution are crucial for building digital human model, and more specifically,for monitoring the neurological conditions. Magnetic resonance imaging(MRI)provides satisfactory spatial resolution,but is not applicable to patients with metal implants(e.g.,heart valves,pacemaker for heart arrhythmias,cochlear implants for hearing loss,etc.) as the powerful magnets cause the implants to move, leading to lethal risks. The alternative modality, xray computed tomography(CT),requires the patients to be exposed in the harmful ionizing radiation,arising concern for the cancer induction and also the worry for its application to specific types of patients such as pregnant females and children.Moreover, neither method is suitable for patients who cannot be tested in a limited space using a large non-portable machine. More specifically, considering the scenario that one is attacked by the cerebral stroke, an immediate neuroimaging is crucial for treatment decision making at the first point of contact. The MRI/CT approaches normally require the patient to be transported to the hospital and therefore the treatment might be delayed. The potential safety and portability issues result in a clinical consequence that a certain range of patients cannot be imaged successfully using MRI and/or x-ray CT due to the reasons aforementioned. In addition,the application of these approaches might also be limited because of relatively high cost and long examination period.

Ultrasound, on the other hand, is a type of mechanical wave delivering the advantages of being fast, safe, portable,and affordable,compared to MRI and x-ray CT.However,conventional ultrasound modalities face difficulties in imaging the intracranial soft tissue surrounded by the skull at high spatial resolution.[1,2]The most common approach, pulse-echo B-mode sonography,[3,4]takes advantage of back-scattered reflection signals to image the tissue. Although weak backscatterings have been used in the imaging of inhomogeneous tissues, in this approach adopted is a model where the sound velocity is assumed to be homogeneous for most of the targets of interest,Surely,this approach is suitable for the imaging of most soft tissues with a nearly constant sound speed. Nevertheless, the speed of sound in the bone is significantly different from that of the adjacent soft tissue, making the uniform velocity assumption broken. Moreover,the back scattered signals are usually dominated by the strong reflections and multiples scattering generated due to the existence of bone. It prevents from clearly probing the much weaker back scatterings produced by small impedance contrasts existing in the intracranial soft tissues. The correlated pulse-echo images are likely to be noisy. Some techniques such as phase-shift migration[5]and raytracing[6]may help to improve the ability to utilize the reflected energy, however, prior knowledge of the sound velocity is still mandatory to correctly migrate the time-variant signal to its spatial origination. Another ultrasound modality is ultrasonic computed tomography,which is powerful in quantitatively reconstructing the sound speed model of the human body. Ultrasonic computed tomography includes diffraction tomography[7,8]and ray-based firstarrival travel-time tomography.[9,10]The diffraction approach provides higher resolution but is much more time consuming and labor intensive, resulting in difficulties in practically automating. Ray theory assumes that the effects of transmission through a heterogeneous medium can be represented by the change of arrival time. Note that it is not necessary to assume the ray to be straight if one performs raytracing or the Eikonal solver. However, the resolution of such an approach is limited to the diameter of the first Fresnel zone,proportional to wavelength.[11,12]Consequently,the associated images lack acceptable resolution as the recorded transmitted signals are dominated by low frequencies. Also, ray-based approaches are known to suffer from detecting low velocity anomalies.

It has been stated that the major issue of intracranial imaging is that the currently observed data do not meet the requirements for the existing ultrasonic modalities. For improving observations,the potential workaround is to either take advantage of natural openings existing in the skull[2]or process part of the bone.[13,14]The former dramatically constrains the illumination as the natural acoustic windows in the skull exist only in limited positions and areas, such as the temporal region and the occipital bone. The latter is an invasive approach such that it is of great possibility to be limited into a narrow range of scenarios in clinical practice. Instead of looking for a compromised workaround, the ambitious goal is to seek a more suitable method that fully uses the recorded wavefields to produce high fidelity images.

The full-waveform inversion (FWI)[15,16]technique formulates an ideal candidate in better taking advantage of existing probing techniques. The FWI has been successfully applied to imaging the subsurface reservoirs for oil and gas industry.[17]With a higher computational cost, the FWI provides much finer resolution than pulse-echo sonography and time-of-flight(TOF)tomography. Travel-time tomography inverts for a sound speed velocity model that generates the firstarrival time identical with the observations,whereas FWI aims at reconstructing a high-resolution sound speed velocity model that best explains the full recorded wavefields. The improved resolution of FWI image is introduced via, among others, a more complete description of the phenomenon of the physical finite-frequency wave propagation through the heterogeneous medium,than the case of ray theory. Such an appropriate description is achieved by numerically solving wave equation that takes into consideration the weak scattering of the intracranial diffraction, in addition to the strong reflections,refraction and multi-scattering of the bone. Consequently,FWI transforms those signals associated with the sub-Fresnel zone heterogeneity(e.g.,weak scatters)into the model parameters(e.g.sound speed)by iteratively solving a non-linear inverse problem, to gradually improve the quality of imaging.The spatial resolution of FWI image is approximately half of the wavelength,corresponding to millimeter or sub-millimeter level in terms of sub-megahertz frequencies.

In practice, the alternate family of kinematic-driven waveform inversion is more robust (e.g., to mitigate cycle skipping issues) for dealing with realistic problems than the classic FWI,as the amplitude information is difficult to accurately simulate by using the wave equation that does not describe the complete physics. To the best of our knowledge,the earliest one of such a family is wave-equation traveltime inversion(WTI)proposed by Luo and Schuster,[18]and more recently,the principle has been extended to Wiener filter based adaptive techniques[19,20]to achieve zero timelags between observed and computed signals.

The FWI has been successfully applied to the ultrasound imaging of soft tissues[21,22](e.g., female breasts). More recently, there was an increased interest in using FWI for hard tissue imaging,especially in solving the bone-related imaging problem.[12,23]However, there is no perfect technique: based on the experience of earth imaging,conventional least-squares FWI suffers from local minima issue during inversion.The solutions are to provide a complete acquisition for improving the illumination, signals consisting of low frequencies to widen the attraction basin of inverse problem, and a good initial model to reduce ambiguity.Compared with the single-side observation system in geophysics,medical imaging can provide full-azimuth acquisition and controllable sources,which allow FWI to be sensitive to all micro-structures inside the brain in a robust manner.In this work,we present a novel modified timedomain waveform inversion technique that properly reconstructs the brain within the skull starting from scratch (a homogeneous water sound speed model). Note that the FWI can be implemented in either time-domain or frequency-domain.The latter is more flexible and efficient in two-dimensional(2D)case,but its three-dimensional(3D)extension will be extremely memory demanding beyond the existing realistic computational condition. Time-domain will be a more appropriate option considering the future application.

In the scope of medical imaging, the importance of investigating FWI has at least two folds: (i)it helps to develop a flexible ultrasound intracranial imaging modality that provides a comparable high-resolution to MRI and CT;(ii)it is promising for building a detailed digital human model of acoustical parameters,as the reference for future ultrasound medical imaging studies.

In this work, we build two reference models by filling the sound speed parameters intoin vivox-ray CT produced structures for a 65-year-old male and a 52-year-old female,respectively. We perform numerical simulations in order to obtain the observed ultrasonic signals. The acquisition is as presented in Fig.1. The transducer is activated separately in turn as a source of ultrasound energy, and the energy is recorded by every other transducer to formulate a full-matrix dataset.We trigger off 48 sources in total and the receiver number is always 288. Starting from those signals and a homogeneous initial velocity model, we perform the proposed multiscale deconvolutional waveform inversion(MDWI)to iteratively update the parametric models of the human brains.Note that with this configuration, we are starting from the scratch(i.e., without any a prior knowledge of the brain) to image the micro-structure of the brain surrounded by the skull. By deconvolutional waveform inversion,we mean that we evaluate the similarity between observed signal and synthetic signal through their limited length Wiener filter, rather than the L2 norm adopted in conventional FWI.The length of filter is reduced stage by stage to formulate a multiscale approach. In practice, the MDWI is a modified version of adaptive waveform inversion (AWI)[20]by introducing the user-defined parameter filter length, but the workflow does not require the subsequent L2 FWI to refine the details. Note that we use numerical experiments such that the observed and synthetic data refer to the signals associated with the reference and reconstructed models,respectively.

Fig.1. Ring array acquisition: a circular curve consisting of 288 transducers in totally surrounding the horizontal section of the brain.

The rest of this paper is organized as follows: in Section 2, we introduce the theoretical method in mathematical detail. In Section 3, we demonstrate the imaging results for the synthetic experiment to illustrate the effectiveness of our proposed approach. Finally, in Section 4, we discuss the advantages and disadvantages to indicate the scope of clinical applications and the scientific insights.

2. Methods

In the section,we will introduce the classic time-domain full waveform inversion technique and propose a novel alternative for dealing with the local minimum issue.

2.1. FWI algorithm

The FWI seeks for parametric models that can numerically explain the observed ultrasonic data.It solves the nonlinear local optimization problem in the least-squares sense. The solution of such a problem consists of several important steps,including but not limited to the definition of misfit function,the model parameter updating, the gradient of misfit function with respect to the model parameters, the inverse of Hessian,and resolution analysis. We will introduce step by step as follows. Also, the readers can refer to Refs.[15–17]for the details of this framework.

2.2. Misfit function

The FWI minimizes a so-called misfit function defined as the L2 norm of the difference between the observed and predicted data(numerically simulated by using the the propperties of the reconstructed model),reading

whereCis the misfit function,pis the predicted data calculated in a given acoustic modelm,anddis the observed data.Independent variabless,r,andtcorrespond to the source,receiver,and time-independent variables,respectively. For fixedsandr,p(t) ord(t) represents a time series recording for a single source-receiver pair. We use notationsmeto represent the acoustic model for the ground truth. Thus, the observed data for numerical tests described in the“Results”section are generated by numerically solving wave equation in the modelme.

2.2.1. Model parameter update

The minimum of the misfit functionCrequires an initial guess of model parameters. We denote the initial model asm0.In the framework of Born approximation, the updated modelmcan be expressed as the sum of the initial modelm0and perturbation model Δm, that ism=m0+Δm. A subsequent Taylor expansion for the misfit function results in

where the superscript ofmirefers to thei-th spatial point on the assumption that the space can be expressed as a vector of sizeM. The partial derivative with respect tomileads to

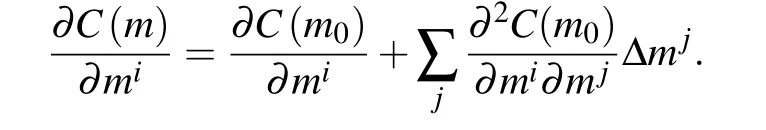
The minimum point ofCis associated with zeroed first order derivative such that the term on the left-hand side of equation vanishes,reading

To obtain the perturbation model,one shall search in the opposite direction of the first-order derivative(i.e.,gradient)of the misfit function at modelm0.The second order derivative of the misfit function refers to the Hessian,which defines the curvature of the misfit function atm0. The relationship between the data and the model is nonlinear such that one needs to iterate the above procedure several times to converge toward the minimum of the misfit function. We define the updated model at iterationiasmiand the iterative update can be expressed as

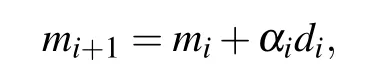
whereαiis the scalar weight which can be obtained by line search method anddiis the decent direction associated with the gradient.In this work,we always follow wolf condition[24]to perform line search for obtainingαi. The simplest decent direction is obtained by steepest decent method taking the opposite direction of gradient, whereas considering the inverse of Hessian helps the gradient to better approximate Δm. The obtention ofdifor this study will be delineated later.

2.2.2. Gradient

The gradient is crucial for deriving the updating direction.In this paper, we specifically consider the isotropic acoustic wave equation

whereurepresents the time-dependent wavefield of the whole space,Δthe spatial Laplacian operator,Ωthe source wavelet depending ont, andK(x,r) the mask operator to restrict the wavefield to receiver positions. The gradient ofCwith respect tomcan be derived by using the Lagrangian multiplier method,namely the adjoint-state technique,[25,26]reading

where*denotes the conjugate andgis the residual wavefield by backpropagating the adjoint source,reading

By back-propagation we mean solving the wave equation for the current modelmi,by injecting the adjoint source at receiver positions in a reversed time order.

2.2.3. Inverse of Hessian

We resolve the nonlinear optimization problem by using the famous gradient descent method, specifically thel-BFGS method(a type of approximate Gauss–Newton algorithm,see Ref. [24] for a review) in this work. The idea is to explicitly approximate the inverse of Hessian at iterationiby using the decent direction of previous iterations,and the inverse of Hessian will be applied to the gradient to formulate a better decent direction for the current iteration. By doing so, the convergence speed can be enhanced.

In our implementation, thel-BFGS takes the following decent direction:

whereQiis thel-BFGS approximation of the inverse Hessian operator ∇2miC(mi) by using several previous decent directions.Note that one may provide an initial estimation of the inverse of Hessian as a precondition, that is, the computation ofQiinvolves the multiplication with the preconditioner in addition to conventional combination of previous decent directions. The preconditioning further enhances the convergence rate. Please see Ref.[24]for more details of this approximation.

2.2.4. Resolution analysis

The link between the acquisition geometry and the spatial resolution of FWI has been well established in the theoretical framework of the generalized diffraction tomography.[27,28]The gradient of FWI, formulated by the interaction of a source wavefield with the residual wavefield,inherits the harmonic nature of the wavefields used to compute it in the space domain.[29]Among others, through the plane wave decomposition analysis, the harmonic nature involves a model wavenumber vector that describes the resolution and dip at an imaging/gradient spatial point. The model wavenumber vectorkis given by the sum of source wavefield wavenumber vector and residual wavefield wavenumber vector(ksandkr,respectively),[30,31]reading

whereωis the angular frequency with a unitnnormal to a potential scattering interface,andvis the local speed of sound at the imaging point. See Fig.2 for an illustration. Be aware that this analysis is also validated for time-domain FWI approach,as it is equivalent to simultaneously invert data of multiple frequencies for obtaining the model parameters.

Fig.2. Illustration of resolution analysis. Among others,ps,pr,q are the slowness vectors in diffraction tomography.

Consequently, in a straightforward way, we see that the circular acquisition helps to enrich the scattering angle contents,leading to a complete wavenumber reconstruction of the model.Note that the diving waves,refraction,and post-critical reflections contribute to low-to-intermediate wavenumber contents of the reconstructed model,whereas the narrow-angle reflections contribute to high wavenumber updates of the model.

2.3. MDWI algorithm

The appropriate modification of the FWI misfit function can improve the probability of converging towards the point close enough to the global minimum. Along this line, AWI,a sophisticated approach proposed by Warner and Guasch,has been successfully applied to subsurface imaging[20,30]and brain imaging,[12]favored by its immunity to cycle skipping issues. The key idea of AWI is that it aims at driving the timedomain matching filter between predicted and observed data into a zero-lagged delta function. In principle,the idea of reducing flying-time lags for band-limited data in the framework of wave equation was introduced by WTI.[18]In practice,AWI is an improved approach proposed by Luo and Sava,[19]by adding a normalization term to the misfit function to reduce the influence of amplitude inaccuracy,reading

whereT(τ) is the weighting function, designed to make the minimum value ofCcorrespond to a zero-lag delta function shape,andwrepresents the Wiener filter,denoted by

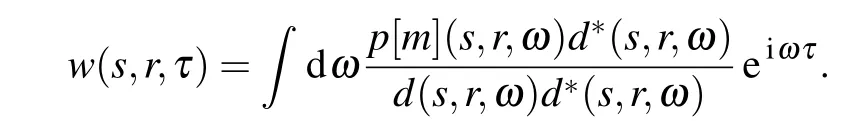
For the derivation of the gradient ofCwith respect tomi,the only difference from conventional FWI lies in the adjoint source being taken into consideration,which reads in this case

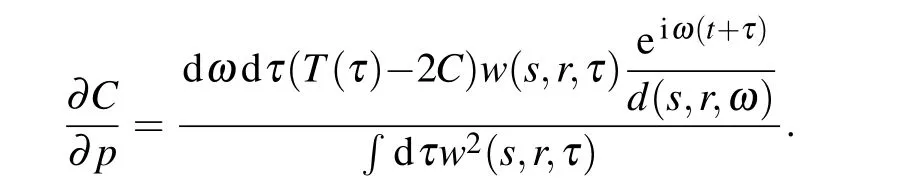
Once the adjoint source is constructed,we can follow exactly the same path as conventional FWI,except injecting different back-propagation sources at the receiver positions. By simply tweaking the misfit function and accordingly the adjoint source,the robustness of waveform inversion will significantly improve.

There are two critical points for achieving a successful implementation:the choice ofT(τ)and the choice of the filter length ofw(τ). On the one hand,the AWI authors mentioned that the choice of weighting functionT(τ)is critical for a robust and rapid convergence.In early stage,T(τ)=τ2was proposed as an analogous to the correlation-based method. Later,the AWI uses the Gaussian filter to formulate a maximization problem. Although it is not shown here, we can compare the performances between different weighting functions and finally takeT(τ)=|τ|/τmaxas the best practice to perform deconvolutional waveform inversion. To the best of our knowledge, such a weighting function has never been applied before. On the other hand,the inventors of AWI have discussed the importance of choosing an appropriate maximum timelag(i.e.,τ ∈[-τmax,τmax]). The increased length of Wiener filter is correlated with the improved robustness and decreased resolution. In practice, we exploit such a feature to extend AWI to a multiscale hierarchy approach, namely MDWI. We set the maximum timelag of Wiener filter to be maximal expected TOF difference for the early arrivals or the dominantfrequency dependent period.We take the relatively small value between the two values. We split the inversion into several stages according to different maximum timelag values. For the initial stage,we choose the maximum timelag value based on the aforementioned principle. In the subsequent stage, we divide the maximum timelag value by two and keep the value unchanged in the same stage. For the experiment conducted in this work,the initial maximum timelag is 5 μs as the dominant frequency is 200 kHz. We perform 4 stages in total and the associated maximal timelags read 25,12.5,5,and 2.5 μs,respectively.We always use 100 kHz–300 kHz frequencies for each stage. We perform 100 iterations for each stage.

As a summary, the appropriate choice ofT(τ) guarantees the robust and rapid convergence of the MDWI algorithm,while the hierarchy approach by reducing the length of Wiener filter results in a workflow that focuses on the large-scale structure at early stage and refines the detailed micro-structure at the end. Note that the MDWI is still a data fitting technique,so in an ideal configuration,it should have a resolution similar to that of traditional FWI.Please refer to supporting information for more details about the hierarchy strategy.

3. Results

In this section, we introduce in detail how the numerical observed data are generated by using numerical finitedifference time-domain wave-equation solvers, and what the MDWI imaging results are for the 65-year-old male and the 52-year-old female cases, respectively. In between the two experiments, we present the reflection-based delay-and-sum(DAS) and first-arrival TOF tomography (one may refer to Refs. [9,32] for more theoretical details, respectively) imaging results for the 65-year-old male case to illustrate that the posed problem cannot be dealt with by using the conventional ultrasound modalities.

3.1. Experiment setup

In the following experiment,we take a slice of thein vivox-ray CT produced structure and then convert the Hounsfield unit values into sound speed to build the ground truth reference. We follow the approach in Ref. [33] to convert Hounsfield Units (UT) to the acoustical properties. Specifically,CT values lower than 0 HU are set to be zero,which is later used as water velocity 1500 m/s. The CT values greater than 1700 HU are set to be 1700, which is used to mimic the maximum p-wave velocity for the cortical bone of the skull with a value of 3100 m/s. The model is linearly interpolated to meet the need for the numerical simulating of the ultrasound propagation. Note that the original resolution of CT image is around 0.5 mm, and we interpolate the image to reduce the grid size to 0.4 mm.

We perform 2D staggered-grid finite-difference timedomain (FDTD) modeling[34]to obtain the observed numerical signal. The FDTD approach is of 4th order in space and 2nd order in time,with a convolutional perfectly matched layer to remove artificial reflections from numerical boundaries.What is solved by the numerical solver is a 2D,isotropic,constant density, acoustic wave equation. To keep the fullwave simulation stable and accurate, 12 spatial points (along both directions)per minimum wavelength are guaranteed during the modelling to avoid numerical dispersion,[35]with the time step derived accordingly based on the Courant number for stability reasons.[34]

The 288 transducers are used as receivers, and of them 48 transducers serve as triggering energy in turn as sources, thereby resulting in around 14 thousand sourcereceiver records of acoustic pressure as a full-matrix ring array acquisition. Each record lasts 360 μs. The source wavelet has a peak frequency of 200 kHz,with useful bandwidth spanning from 100 kHz to 300 kHz for FWI.During the inversion stage,we assume that the source signature is unknown and estimate the wavelet of every individual source to avoid the influence of data inconsistency on imaging. We always start from homogeneous water speed to update the brain slices in both cases.

3.2. MDWI results for a 65-year-old male case

The model considers a brain transverse section of a 65-year-old male. The size of the selected slice is of an approximate eclipse shape: the length of short axis and long axis are 100 mm and 150 mm, respectively. We place the transducer,a circle of 220 mm in diameter,surrounding the brain and we assume that the gap has been filled in with water. In such a case, the best illumination can be provided for the observation. In the targeted head section,there exist skins,skulls and soft brain tissues. The sound speed in the skull and of the protected brain soft tissue are approximately 3 km/s and 1.5 km/s,respectively. The scatters inside the brain soft tissue are of very small speed perturbation compared with 1.5 km/s, say,the speed difference is less than 0.1 km/s.

Starting from a homogeneous velocity model, we apply the MDWI to sub-megahertz ultrasound data generated by the ground truth model. We show the reconstructed parametric model of the brain tomogram in Fig. 3. We adopt two different colormaps to carefully check the quality of the imaging for various targets.Specifically,limited velocity range emphasizes the intracranial soft tissue imaging,and large speed span highlights the reconstruction of the heterogeneity of the hard tissue. We provide two profiles atX=110-mm position andY=140-mm position, respectively, in Fig. 4 to view the detailed reconstruction. Figures 3 and 4 both illustrate the fact that MDWI finds a model that is highly consistent with the ground truth within a sub-millimeter resolution.

The bone for the selected section has a multi-layered structure, with inner and outer high-impedance contrasts apparent. Such a structure will result in strong signal attenuation in transmitted wave,leading to significant difficulties for manipulating conventional tomography modality. However,if the heterogeneity can be represented by a 0.4-mm grid,we can successfully recover those details in decent agreement with the true model. Inside the skull, we see that the MDWI can produce an accurate quantitative image of the soft tissue, in the sense that the structure and wave speed of the target tissue are properly recovered.

The waveform inversion is a data driven technique. The numerical termination is usually determined by evaluating the data consistency between prediction and observations in most of the cases that we do not have a prior knowledge of the model. We present in Fig. 5 the single source predictions in the initial model and final model, in comparison with the observed signals which are generated from the ground truth model. The comparison shows the final model reconstructed by MDWI properly explains transmissions, refractions, weak and strong scatterings,and even the multiple reflections,as all types of events in the observed data are in good agreement with predictions.

Fig.3. Models of acoustic velocity for 65-year-old male case: top row refers to ground truth and bottom to the reconstruction by MDWI.Left column is clipped to 1.45 km/s–1.65 km/s for comparing soft tissues in detail,while right column is clipped to 1.45 km/s–3.00 km/s for comparing skulls in detail. See supporting information for intermediate results.

Fig.4. MDWI profiles of acoustic velocity for 65-year-old male case: top two and bottom two rows refer to the profiles of models in Fig.3 at X =110 mm and at Y =140 mm,respectively. For the profiles at the same position,sound speed ranges are different. Blue and red curves correspond to ground truth and reconstructed models,respectively.

Fig.5. Single source recordings for 65-year-old male case: from left to right, recordings correspond to data for initial, reconstructed, and ground truth models,respectively.

3.3. DAS and tomography results for a 65-year-old male case

Now,we come to conduct an ideal synthetic experiment,so that we can circumvent the issues that the wave equation might describe the physics in an incomplete manner.Although we have explained the reason why ray-tracing DAS and firstarrival TOF tomography fail to image the brain, arises the problem whether the model can be properly recovered with conventional ultrasonic modality in such a perfect configuration. We show in Fig. 6 the results of ray-tracing DAS and TOF computed tomography(one may refer to Refs.[9,32]for theorical details, respectively) images by exploiting the same observed dataset as the MDWI modality in the case of 65-yearold male. Be aware that we assume constant velocity to process the reflection radio frequency data in the ray-tracing DAS case. The weak scattered signals cannot be properly imaged due to incorrect wave speed assumption. Only the external layer of the bones can be accurately recovered, whereas the images of the internal layer are not very well focused. The tomogram is generated by using first arrival adjoint tomography based on the Eikonal equation,[36]which properly takes the refraction into account.Despite solving a nonlinear optimization problem, the resolution of this approach is still relatively low within the diameter of the first Fresnel zone(around 20 mm in this case),compared with the target of interest.Only the macro structures of the hard tissue and soft tissue have been captured in an obscure manner. In this subsection explained is that the DAS and first-arrival tomography methods encounter difficulties in resolving the brain imaging problem for the cases in which MDWI works.

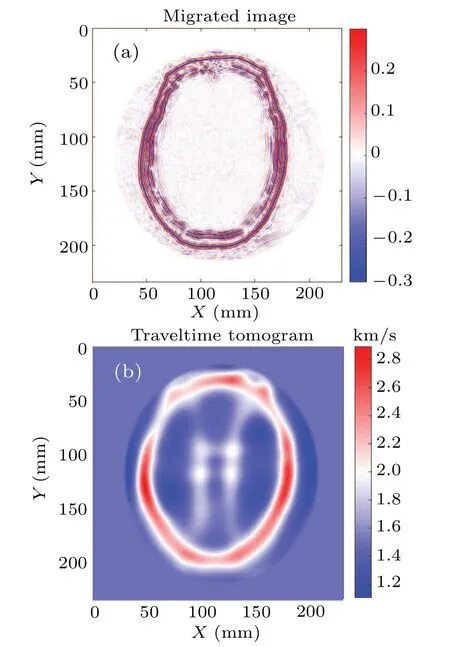
Fig.6. Models for 65-year-old male case: Panels(a)and(b)represent the ray-tracing DAS and TOF tomography wave speed models,respectively. Be aware that the DAS result is obtained by using radio frequency data without pre-or post-conversion to envelope.

3.4. MDWI results for a 52-year-old female case

The experiment carried out in this subsection is very similar to the one in the 65-year-old male case. The purpose of this subsection is to indicate that the designed algorithm has nice adaptivity and robust features even if the experimental configuration slightly varies.

Fig.7. Models of acoustic velocity for 52-year-old female case: top row refers to ground truth and bottom to reconstruction by MDWI.Left column is clipped to 1.45 km/s–1.65 km/s for comparing soft tissues in detail,while right column is clipped to 1.45 km/s–3.00 km/s for comparing skulls in detail.

We adopt the same strategy, without tuning any parameters, to image the brain of the 52-year-old female. We see in Fig. 7 that the acquisition is not so well-positioned as the previous one, which might happen in practice. The targeted model contains weaker scatterings than the case of 65-yearold male’s brain section. The maximum bone thickness in this model is relatively large as shown in the bottom right part of the image. Despite a slightly degraded imaging around such an area, the MDWI reconstructed model still presents a high fidelity between inversion and ground truth, for hard tissue and soft tissue. By carefully checking the profiles presented in Fig. 8, we see that the images around the thick bone (topmost plot forY ∈[175,200]-mm position), for both skin soft tissue and brain soft tissue, show oscillatory characteristics.On the other hand, the double-layered structure of the bone is well explained even for the thickest areas. Comparing the prediction with the observed data,we see no obvious inconsistency in Fig.9. The model error might result in very tiny data difference, leading to difficulties of further refinement of the image through MDWI driven by data fitting.

Fig.8.Profiles of acoustic velocity for 52-year-old female case:top two and bottom two rows refer to profiles of models in Fig.2 at X=110 mm and at Y =140 mm, respectively. For profiles at the same position,sound speed ranges are different. Blue and red curves correspond to ground truth and reconstructed models,respectively.

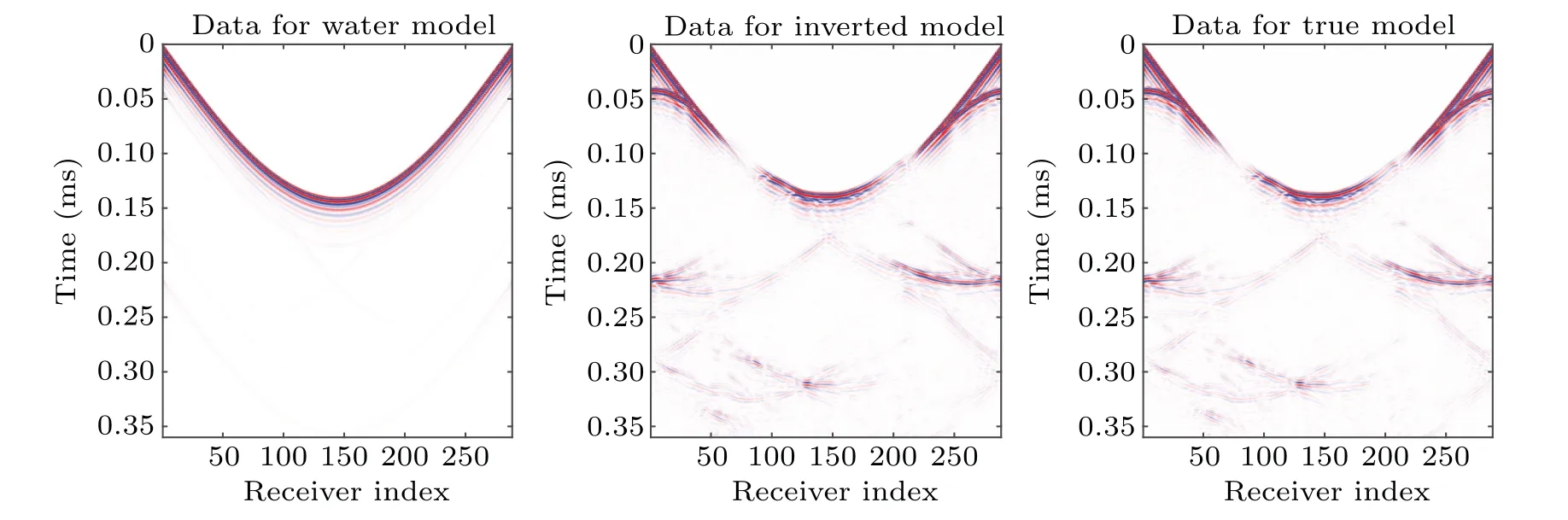
Fig.9. Single source recordings for 52-year-old female case: from left to right, recordings correspond to data for initial, reconstructed, and ground truth models,respectively.

3.5. Discussion,conclusions,and perspectives

Ultrasonic tomography of the full recorded wavefield by using the FWI is a powerful imaging tool, which promises to develop a modality of the same revolutionary influence as MRI and x-ray CT.Conventional ultrasonic methods are universally safe, portable, and affordable, but cannot deliver images at high spatial resolution for brains,whereas the FWI provides a promising remedy regarding this shortcoming by providing high resolution at sub-millimeter level through using sub-megahertz signals of all types of events. Consequently,the FWI significantly mitigates the limitations of conventional pulse-echo sonography,phase-shift migration,and first-arrival TOF tomography.

The experience accumulated in the geophysics community shows that the success of FWI is based on the following requirements: an acquisition providing full illumination, observed data containing sufficient low frequencies, and initial model close enough to the true model. As for the brain imaging problem, the two former requirements are not impractical. The ring array is able to provide circular acquisition and the modern transducer is able to generate sub-megahertz signals transmitting across the head. The dedicated MDWI technique proposed in this article can start from a homogeneous model of water speed to converge towards the right answer,which significantly releases the requirement for initial model.In addition, by manipulating the length of wiener filter, the MDWI delivers a similar resolution to the conventional FWI at the final stage. We do not have to use one waveform approach to build the initial model,and switch to another waveform method later for improved resolution. To clarify,we use water homogeneous velocity model to justify the robustness of proposed approach, but it is not necessary to always start from the homogeneous velocity model,as a prior information can significantly improve the convergence speed to reduce the computational overburden.

The gaps,between the synthetic experiment described in this article and a realistic clinical application of MDWI, are mainly threefold: the 3D extension,the wave-equation solver considering more physical properties, and a more computational efficient implementation. First,we shall extend the acquisition from the circular ring array to a spherical helmetbased array. The extension to 3D case allows the MDWI to accurately consider the off-plane waves caused by irregular shape of the skull. By three dimensions,we mean that the data are acquired and inverted both in three dimensions. Second,in this work,we consider the simple isotropic constant density wave equation. This is reasonable for the inversion of wave speed at low frequencies,as many studies indicate that the coupling effect across different parameters are not significant at low frequencies and the sound speed parameter will dominate the inversion. However,if the finer images can be obtained by considering much higher frequencies,the introduction of density, attenuation and/or anelastic effects will be desired and inevitable. That is, the introduction of viscoelastic forward modeling engine will be crucial. Third, the FWI is a computationally intensive technique. Its alternative MDWI requires almost the same numerical cost. Each image presented in this work takes 9 hours to build,running on the CPU-based cluster and taking up 288 cores. However,as a research-oriented experiment,we consider significantly redundant time samplings,source numbers and spatial grids. The ideal 2D experiment needs only half of the computational time. We perform the MDWI by using 24 Intel Xeon E5-2680 v3 Haswell CPUs in total, for which the peak performance is 0.9 tera-flops. In a similar running time, an optimized 3D implementation needs 1000 times the computational resources of the 2D version,equivalent to 0.9 peta-flops. The brand-new high-performance GPU-based workstation, DGX-A100, can provide the peak performance of up to 5 peta-flops. Consequently,it is achievable to reduce the computational time to less than half an hour with the most advanced A100 graphic cards. Moreover, the required iterations for convergence can be greatly reduced by starting from the first-arrival TOF tomography model with preconstructed bone structures. Such a model can be easily obtained by using the existing modalities in real time. Another additional remedy is to explicitly consider the structure of the Hessian matrix for preconditioning the inverse problem. The emerging artificial intelligence approaches can also be adopted to solve part of the inverse problem in a pre-trained manner for reducing the computational intensity. Note that the discussion in this section only accounts for time-domain waveform inversion. The frequency-domain counterpart faces a different numerical challenge,say,the extreme demand for memory in 3D case,which is beyond the scope of this work.

Despite an intensive computational cost,the FWI(specifically MDWI) promises to provide a safe, portable, and affordable ultrasonic imaging modality that provides a submillimeter spatial resolution by using sub-megahertz signals.The approach works better than conventional ultrasound techniques in dealing with intracranial imaging problems. Fortunately,the major drawback of such a method can be mitigated,which benefits from the development of GPU-based high performance computational hardware. Once the numerical cost does not prevent it from being put into practical clinical application, FWI/MDWI will formulate a powerful and flexible tool for monitoring the neurological conditions. More importantly, as a greater blueprint, the emergence of FWI/MDWI for quantitative imaging will also lay the ground for building the digital acoustic human body model at high spatial resolution, which will form the reference for the future ultrasound imaging research.

Acknowledgements

The authors would express their gratitude to the Fourth Affiliated Hospital, Zhejiang University School of Medicine,for providing x-ray CTin vivomodel of 65-year-old male and 52-year-old female. Also, the authors would extend their appreciation to professors Hailan Zhang and Hao Chen,from the Institute of Acoustics,Chinese Academy of Sciences,for their suggestions in inhomogeneous acoustic models.

Project supported by the Goal-Oriented Project Independently Deployed by Institute of Acoustics,Chinese Academy of Sciences(Grant No.MBDX202113).