新建曲线地铁盾构隧道下穿施工引起的既有隧道沉降分析
江 杰,龙逸航,欧孝夺,邢轩伟,张 探
(1.广西大学 土木建筑工程学院,广西 南宁 530004;2.广西大学 工程防灾与结构安全教育部重点实验室,广西 南宁 530004)
随着中国城市地铁网络的快速发展,新建地铁隧道难以避免下穿通过既有运营地铁隧道;同时,受周围建筑环境的影响,会将新建线路设计为曲线线路。曲线地铁盾构隧道下穿既有隧道施工期间,盾构转弯通过曲线线路时会对弯道内侧土体进行超挖,使既有隧道两侧产生的沉降不同,情况更为复杂。因此,研究曲线地铁盾构隧道下穿施工引起的既有隧道沉降具有重要的意义。
由于曲线盾构隧道施工的复杂性,目前该领域的相关研究较少。路林海[1]和Zhang[2]等利用数值模拟研究了曲线盾构隧道引起的地表沉降;孙捷城等[3]基于Mindlin解推导了曲线盾构开挖引起的地表变形公式;邓皇适[4]和Li[5]等结合镜像法[6]提出曲线盾构隧道施工引起地表沉降的简化理论。但以上研究均集中于研究地表沉降方面。
近年来,对于新建盾构下穿既有隧道方面的研究主要采用数值分析、模型试验和理论分析等方法。数值分析法是利用有限元[7]、离散元[8]和有限差分[9]等模拟软件建立仿真模型进行研究。模型试验法是通过建立室内模型模拟实际工程,测量结构的受力特性;按试验条件可划分为常重力模型试验[10]和离心模型试验[11–12]。理论分析法是利用数学和物理理论推导工程结构响应的相关公式进行研究,具有概念明确和易于应用的优点,被多数学者采用,例如:Klar等[13]利用连续弹性理论研究了新建隧道施工对临近既有管道的影响;张治国[14]和Zhang[15]等运用Winkler地基理论,研究了多种不同工况下新建隧道施工对既有隧道的影响;梁荣柱等[16]将既有隧道视为Timoshenko梁,计算过程考虑了既有隧道剪切刚度削减效应;可文海等[17]在计算过程中运用了能够考虑土体剪切效应的Pasternak地基模型,并分析了该模型不同剪切系数对既有隧道的影响;代仲海等[18]运用极限分析上限定理研究了盾构开挖面极限支护力。但上述文献均未见有对曲线盾构下穿既有隧道沉降展开研究。
鉴于此,首先,基于前人研究,引入镜像法和Mindlin解计算曲线盾构转弯超挖间隙和不平衡施工因素引起的额外土体位移,结合修正Loganathan法构建能够计算新建曲线盾构施工引起的3维土体竖向位移的模型。之后,将土体竖向位移视为位移荷载施加在既有隧道上,基于能够考虑剪切效应的Pasternak地基和Timoshenko梁理论构建关于既有隧道沉降的控制方程,运用有限差分法对方程降阶并求解;最后,通过与实际工程监测数据对比验证该理论方法的正确性。
根据上述分析与实际施工的情况,建立曲线地铁盾构隧道下穿施工期间的掘进模型,如图1所示。
图1中,x方向平行于既有隧道,y方向为盾构掘进的方向,z方向为隧道埋深的方向,H为刀盘中心处距地面距离,盾构开挖面位于y=0处的xoz平面。
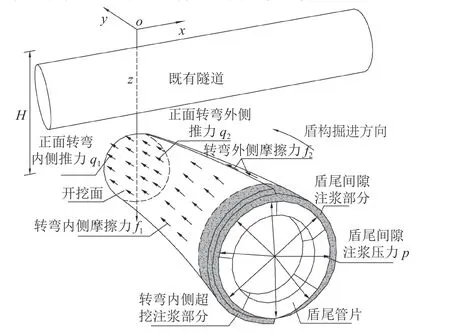
图1 曲线盾构下穿既有隧道计算模型Fig. 1 Calculation model of the curved shield under traversing existing tunnel
将曲线地铁盾构隧道施工引起的作用于既有隧道上的土体竖向位移uz(x)分为3部分。第1部分,uz1(x)为盾构机外径与隧道衬砌外径之间的物理间隙带动周围土体向间隙移动而产生的土体位移,也称为地层损失;第2部分,uz2(x)为盾构机转弯过程中,由内侧超挖间隙造成的土体位移;第3部分,uz3(x)为施工过程中,由盾构不平衡开挖面推力、盾壳不平衡摩擦力及盾尾间隙注浆压力造成的土体位移。将3部分的土体位移进行叠加,即可得到曲线地铁盾构隧道掘进引起的土体竖向总位移uz(x):
1 曲线地铁盾构隧道施工引起的土体竖向位移计算
1.1 计算模型及假定
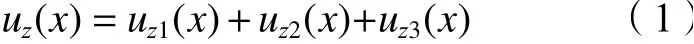
为便于计算,根据前人研究经验[2],建立xyz空间坐标系,并做如下假定:
1)将土体视作均质线弹性半无限空间体,且不考虑排水固结的影响。
2)盾构开挖面附加推力受转弯的影响分布不均,以刀盘中心线为分界线,转弯内侧推力q1与外侧推力q2关系为q2=ξq1(ξ≥ 1),其中,ξ为推力差异系数。
3)盾壳摩擦力同样受转弯的影响分布不均,以新建隧道中线为分界线,转弯内侧摩擦力f1与转弯外侧摩擦力f2的关系为f2=ηf1(η≤ 1),η为摩擦力差异系数。
4)同步盾尾间隙注浆压力p沿盾尾管片圆周径向分布,影响范围为盾尾后方单环管片长度。
1.2 衬砌间隙引起的土体竖向位移计算
盾构与衬砌之间的间隙(地层损失)引起的土体竖向位移uz1(x)可采用Loganathan法[19]进行计算。Loganathan法可计算由盾构开挖引起的任意深度处土体的竖向位移,但该方法假设开挖面离计算点无穷远(y→∞),只能计算2维平面上的土体位移,故需要对公式进行修正。参考张金菊[20]的研究,本文基于Loganathan法推导出3维空间的土体竖向位移计算公式;推导过程中,由于本文计算模型中衬砌间隙发生在盾尾处,故将原公式中的y变换为y+L,如式(2)所示:

1.3 弯道内侧超挖间隙引起的土体竖向位移计算
盾构转弯超挖空隙引起的土体竖向位移uz2(x)可采用镜像法进行计算。对于半径为ar的球形间隙(x0,y0,z0)和其镜像位置(x0,y0,–z0)虚设的同等大小体积膨胀在计算点(x,y,z)所产生的沉降Sz1与Sz2表达式为:
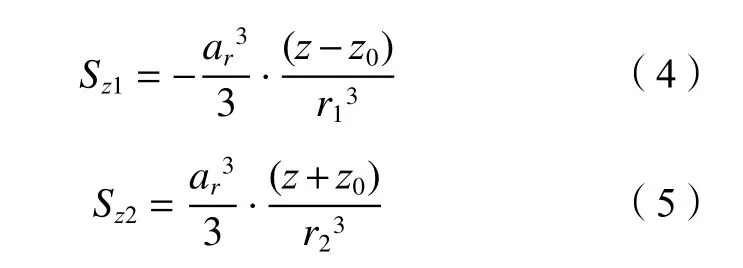
考虑实际边界条件,将式(4)、(5)产生的附加剪应力反向施加于地表,计算点(x,y,z)产生的沉降表达式Sz3为:

获得单位体积空隙产生的土体沉降公式后,通过对盾构转弯内侧超挖的区域进行积分即可得该部分引起的土体沉降。取刀盘内任意位置一微元体进行分析,如图2所示。
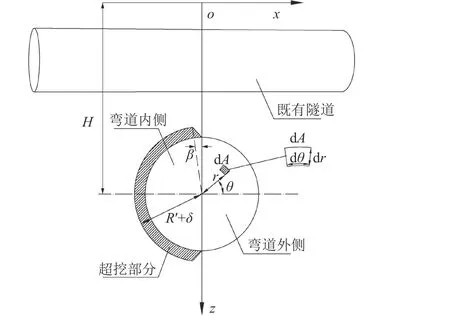
图2 转弯内侧超挖间隙示意图Fig. 2 Over-excavation clearance caused by the inside of the turn
图2中:R′为盾构刀盘半径;dA为刀盘一微元体的面积;r为微元体到刀盘中心点的距离;β为盾构超挖刀伸缩角度,通常为5°~10°;θ为计算微元体与刀盘中心水平线的夹角;δ为超挖量,郝润霞等[23]提出δ可按式(8)计算:
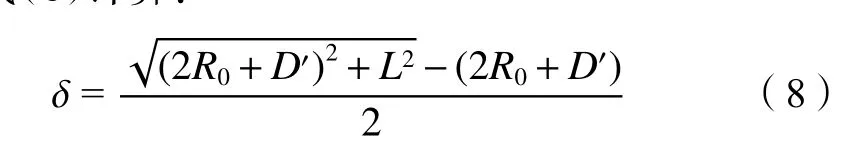
式中,R0为盾构曲线半径,D′为盾构刀盘直径,L为盾壳长度。
由于原坐标系求解较为困难,需进行坐标变化,假设以刀盘中心(0,0,H)为原点,则空隙点(x0,y0,z0)坐标变化为:

将式(9)代入式(4)~(7),对Sz进行积分即可求得盾构转弯时内侧超挖空隙引起的土体竖向位移uz2(x):
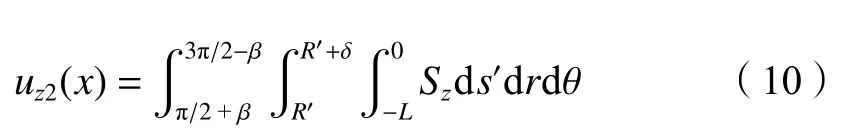
式中,s′为计算点距盾构刀盘的距离(盾构机盾尾至刀盘方向)。
1.4 盾构施工因素引起的土体竖向位移计算
盾构施工工程中,由开挖面附加推力q、盾壳摩阻力f、盾尾间隙注浆压力p共同产生的uz3(x)可基于Mindlin解求出[24]。位于空间坐标(0,0,c)处的水平集中力Ph与竖向集中力Pv引起任意一点(x′,y′,z′)处的土体竖向位移wm1和wm2的计算公式为:

盾构开挖面附加推力q引起的土体竖向位移计算模型如图3所示。
图3中,刀盘上一微元体dA=rdrdθ,微元体上所受的集中力dPhq=qrdrdθ。以刀盘中心(0,0,H)为原点,对式(11)进行如式(13)所示的坐标变换:则可求出由dPhq引起(x,y,z)坐标空间体内的任意一点竖向位移dwmq,如式(14)所示:
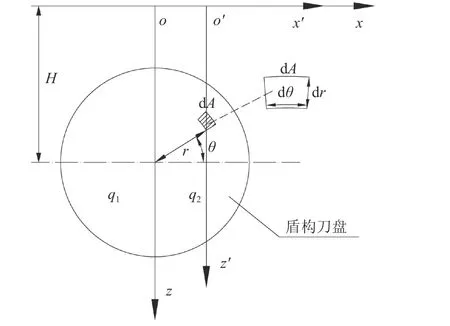
图3 开挖面附加推力引起的土体竖向位移计算模型Fig. 3 Calculation model of soil vertical displacement caused by additional pressure around excavation
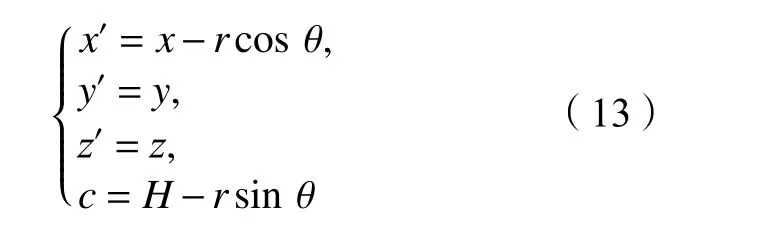

盾壳摩擦力f引起的土体竖向位移计算模型如图4所示。
图4中,盾壳上一微元体dA=R′dsdθ,微元体上所受的集中力dPhf=fR′dsdθ。以刀盘中心(0,0,H)为原点,对式(11)进行如式(16)的坐标变换:
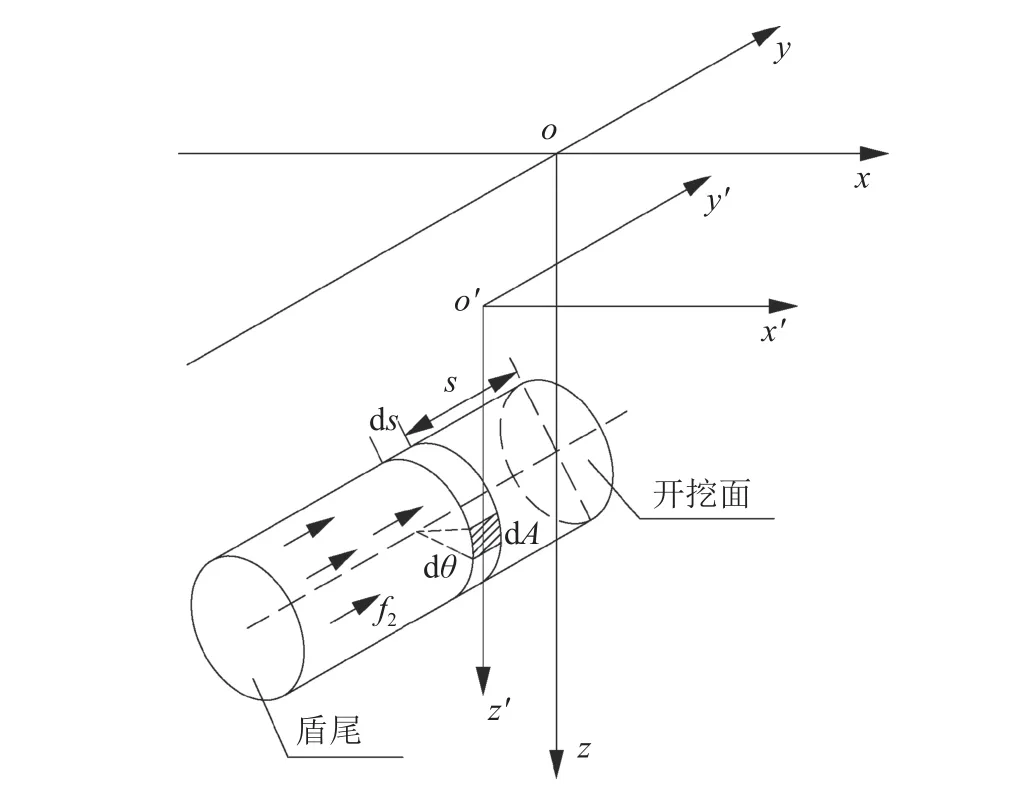
图4 盾壳摩擦力引起的土体竖向位移计算模型Fig. 4 Calculation model of soil vertical displacement caused by friction forces around shield skin
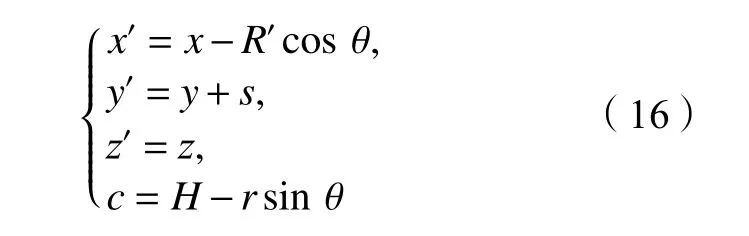
则可求出由dPhf引起的空间体任意一点竖向位移dwmf,如式(17)所示:

盾尾间隙注浆压力p引起的土体竖向位移计算模型如图5所示。
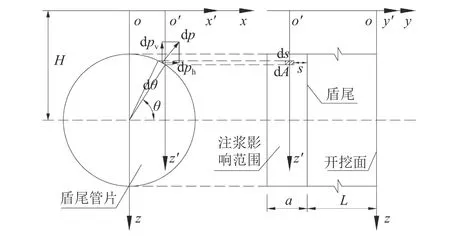
图5 盾尾间隙注浆压力引起的土体竖向位移计算模型Fig. 5 Calculation model of soil vertical displacement caused by synchronous grouting pressure
图5中:a为盾构注浆影响范围的长度,通常取单环管片的长度;盾尾注浆影响范围内微元体dA=R′dsdθ;微元体上所受的集中力dPp=pRdsdθ,可分解为水平分力dPhp与竖向分力dPvp,对于水平分力dPhp引起空间体内的竖向位移较小,本文不进行考虑。以刀盘中心(0,0,H)为原点,对式(12)进行如式(16)所示的坐标变换即可求出dPvp引起空间体内的任意一点位移dwmq,如式(19)所示:

将式(2)、(10)、(21)代入式(1)即可获得曲线地铁盾构隧道掘进引起的作用于既有隧道上的土体纵向总位移uz(x)。
2 土体与隧道相互作用分析
2.1 计算模型及假定
获得新建曲线地铁盾构隧道施工引起的土体竖向位移场uz(x)后,可将既有隧道处的土体位移视为位移荷载施加在既有隧道上,从而求出既有隧道的沉降。研究表明[16–17],Tiomoshenko梁能够考虑既有隧道的剪切效应,Pasternak地基能够考虑土体的连续性影响,均能够较好地模拟实际情况。本文结合Timoshenko梁和Pasternak地基建立土体与隧道相互作用计算模型(T–P模型),如图6所示。

图6 土体与隧道相互作用计算模型Fig. 6 Calculation model of soil-tunnel interaction
为方便阅读,设wz(x)为既有隧道沉降,Wz(x)为地基反力。基于Pasternak地基理论,Wz(x)与Uz(x)分别为:

式(24)~(25)中,Q为既有隧道微元附加剪力,M为既有隧道微元附加弯矩。
由于常规条件下附加剪力Q和附加弯矩M的获取较为困难,需将其转换为关于既有隧道沉降wz(x)的方程,根据Timoshenko梁理论,附加剪力Q、附加弯矩M的表达式为:
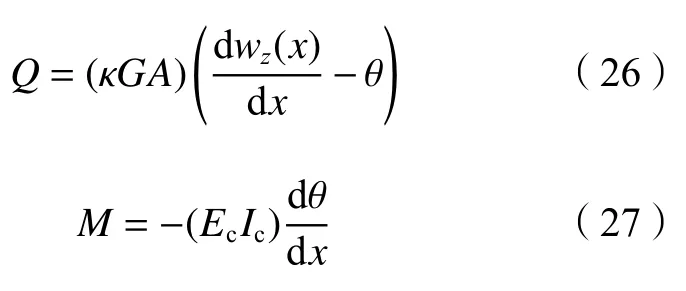
式(26)~(27)中:EcIc为既有隧道等效抗弯刚度;κGA为既有隧道等效剪切刚度,可按照文献[16]提出的方法计算,本文不再详述。联立式(22)~(27),省略高阶微量,可得到仅关于土体竖向位移uz(x)的既有隧道沉降wz(x)的控制方程:
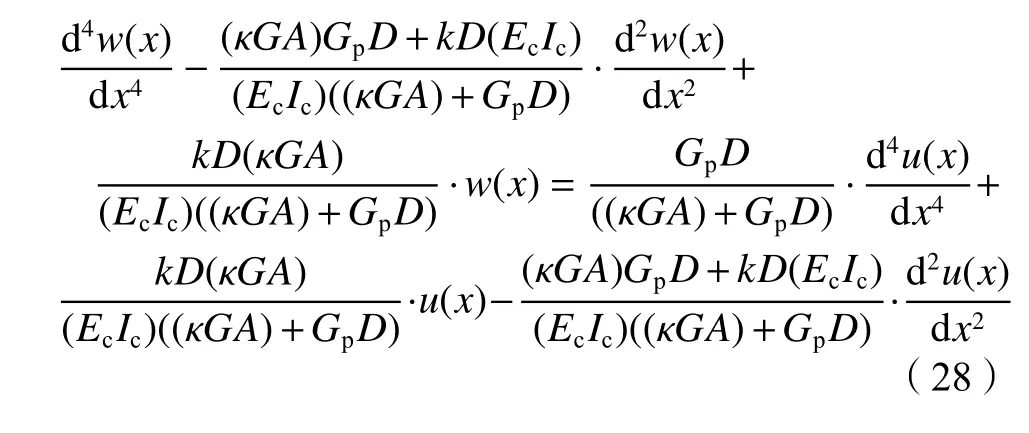
2.2 既有隧道沉降的有限差分解
由于式(28)为4阶常微分方程,不便于直接求解,故采用有限差分法对其进行降阶处理。对既有隧道进行离散,划分为n个长度相等的单元,并在隧道两侧增加2个虚拟节点,每个单元长度为l,如图7所示。
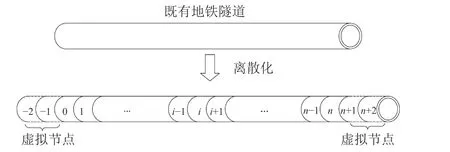
图7 既有隧道节点的划分Fig. 7 Existing tunnel node division
利用有限差分标准格式对式(28)进行处理:

求解式(29)还需要w–1、w–2、wn+1、wn+2(当i=0或n)虚拟节点的表达式,可根据既有隧道边界条件获得。假设既有隧道足够长且隧道两端剪力和弯矩为0,既有隧道附加剪力Q和附加弯矩M关于沉降uz(x)的公式可联立式(22)~(27)获得,采用有限差分格式进行处理后为:
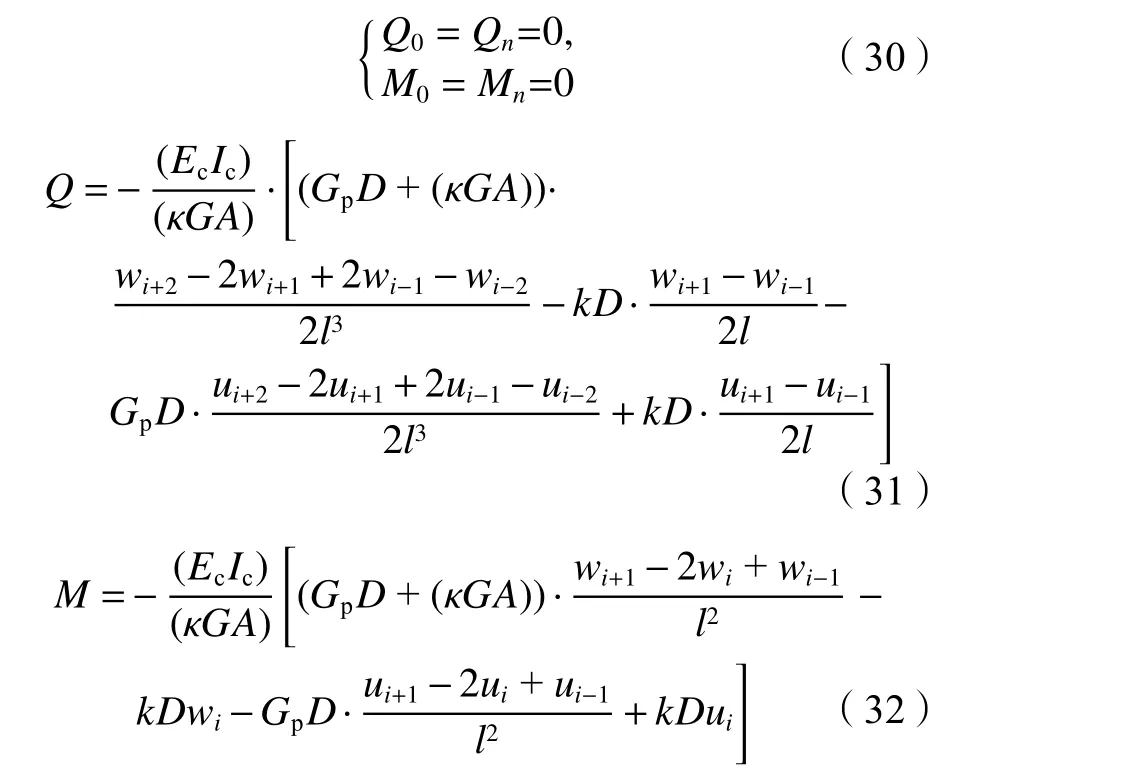
联立式(30)~(31)可得到既有隧道两端4个虚拟节点的表达式:



3 实例验证
南宁某新建地铁盾构下穿既有运营地铁隧道区间线路为曲线,转弯半径R0为300.00 m,采用泥水盾构机进行施工,盾构刀盘直径D′为6.28 m,盾体的长度L为8.47 m;新建隧道埋深约为25.20 m,半径R为3.00 m,单环管片长度为1.20 m;所处的地层由圆砾和泥岩组成,平均泊松比ν为0.29,平均土体剪切模量G为26.52 MPa。
既有地铁隧道埋深约为13.44 m,所在地层主要由粉土组成,土体弹性模量Es为14.6 MPa;既有隧道管片宽度为1.5 m,采用C50混凝土和HRB400钢筋预预制,既有隧道等效抗弯刚度(EcIc)为9.48×104MN·m,等效剪切刚度(κGA)为3.35×103MN/m。
结合该项目施工的实际情况,各参数取值为下穿区间段的平均值,盾构开挖面推力q为97 kPa,盾壳摩擦力f为80 kPa,盾尾间隙注浆压力p为270 kPa,开挖面推力差异系数ξ为1.1,盾壳摩擦力差异系数η为0.9;参考魏纲[27]对于不同地区地层损失率取值的研究,地层损失率ε0取为0.2%;其余相关计算参数如表1所示。

表1 计算参数Tab. 1 Calculated parameters
选取计算盾构刀盘到达既有隧道前8环(9.6 m)与盾尾离开既有隧道4环(4.8 m)的既有隧道沉降,模拟盾构穿越前、后的工况,结果见图8、9。为方便对比,对第2节中计算的总位移uz(x)进行拆分,分别将盾构施工过程中开挖面推力、盾壳摩擦力、注浆压力产生的土体位移单独视为位移荷载施加在既有隧道上计算其沉降,并与不考虑曲线效应的盾构下穿既有隧道沉降计算值和工程实际监测值进行对比。
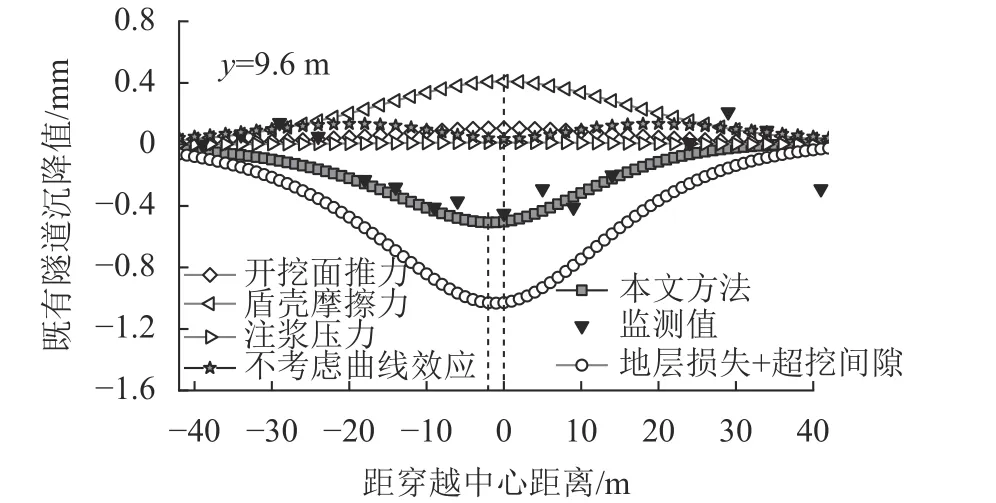
图8 盾构穿越前不同位移荷载引起的既有隧道沉降值与监测数据对比Fig. 8 Comparison of the monitoring data and the settlement values of the existing tunnel before the shield crossing
由图8可知:盾构到达既有隧道前9.6 m时,既有隧道产生了–0.48~0.20 mm的竖向位移,最大位移为–0.48 m。本文方法计算的既有隧道位移均为沉降,最大沉降值为–0.51 mm,位于穿越中心左侧2 m处,沉降曲线为非对称分布。单独作用于既有隧道上的位移荷载中,uz3(x)包括开挖面附加推力、盾壳摩擦力、盾尾间隙注浆压力,均使既有隧道产生隆起;地层损失uz1(x)和超挖间隙uz2(x)使既有隧道产生沉降,且对既有隧道的影响大于uz3(x)。对比不考虑曲线影响的计算结果可以发现,受uz3(x)的影响,未考虑曲线盾构效应下的既有隧道变形整体呈现出隆起的现象,与监测值和本文方法相差较大。本文方法部分超挖间隙造成的沉降抵消了uz3(x)产生的隆起,使隧道总体呈现出沉降的现象;受监测误差影响,既有隧道相邻监测点沉降值出现了上下波动的情况,但总体分布趋势仍为沉降,与本文方法的计算曲线较为吻合。
由图9可知:盾构穿越后相比穿越前,既有隧道产生了更大的沉降,转弯内侧沉降大于外侧,最大监测沉降值为–3.02 mm。盾构穿越后,开挖面推力和盾壳摩擦力使既有隧道产生沉降,盾尾间隙注浆压力仍使既有隧道隆起,隆起值有所增加;地层损失和超挖间隙引起的沉降相比穿越前大幅增加,成为影响既有隧道沉降的主要因素。图9中给出的未考虑曲线盾构影响的既有隧道最大沉降值为–1.82 mm,位于穿越中心,不符合监测沉降分布规律。本文方法的沉降曲线分布具有非对称性,转弯内侧沉降值大于外侧,最大沉降值为–2.89 mm,位于距新旧隧道交界处1~2 m之间,与监测值分布规律较吻合。

图9 盾构穿越后不同位移荷载引起的既有隧道沉降值与监测值对比Fig. 9 Comparison of the monitoring data and the settlement values of the existing tunnel after the shield traversed
此外,图9中本文方法计算曲线的沉降槽宽度略大于监测值,主要是由于本文方法假设土体为线弹性空间体,与实际有一定差异。同时,计算曲线盾构超挖间隙的镜像法通常会高估沉降槽曲线宽度[12],但总的来说,相比仅考虑地层损失的传统方法,本文方法能更好地反映新建曲线盾构下穿施工引起的既有隧道沉降变化规律。
4 既有隧道沉降影响因素分析
为进一步研究新建曲线地铁盾构隧道下穿引起的既有隧道沉降规律,选取既有隧道影响较大的穿越后工况,针对转弯半径R0、盾构刀盘直径D′、新建隧道外径与既有隧道外径之间的竖向间距Zc等参数进行分析;分析过程采用上述案例中的参数,在分析某一参数时,其余参数保持不变。
4.1 新建曲线盾构地铁隧道转弯半径R0的影响
取转弯半径R0为150、300、450、600、750 m进行计算,并与未考虑盾构曲线效应的计算结果进行对比,如图10所示。由图10可知:随着转弯半径R0的减小,既有隧道的沉降逐渐增加,且转弯内侧的沉降值增加幅度高于转弯外侧。工程中,新建盾构线路的曲线半径R0多数为300、450 m。当R0=300~450 m时,隧道最大沉降值与图10中不考虑曲线盾构影响(R0→∞)时的最大沉降值分别相差36.7%和28%;取既有隧道距穿越中心距离为–20 m(弯道内侧)和20 m(弯道外侧)处的沉降值进行对比,R0=300、450 m时,既有隧道位于弯道内侧和弯道外侧的沉降值分别相差22.7%和17.8%。可见新建曲线盾构下穿施工引起既有隧道沉降与直线盾构下穿存在较大差距,本文理论计算曲线盾构下穿工况更具优势,而现有理论计算结果可能会忽略超挖间隙产生的额外土体位移而低估既有隧道整体和弯道内侧处的沉降。
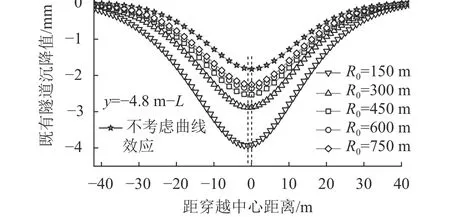
图10 不同转弯半径下既有隧道沉降曲线Fig. 10 Existing tunnel settlement curves with different turning radius
值得注意的是,当R0从300减小至150 m时,既有隧道沉降值增加的幅度明显提升,最大沉降值增加了36%,弯道内侧和外侧的沉降值相差提升至31.6%;当R0为750 m时,既有隧道弯道内侧和外侧的沉降差距较小,与未考虑盾构曲线影响所计算的沉降也相差较小。因此,工程中,当R0大于600 m时,可以忽略曲线盾构超挖的影响,即视为直线盾构下穿施工;特殊情况,R0设计小于300 m时,应提高既有隧道的监控等级。
此外,由图10还可以看出,转弯半径R0的变化并未改变既有隧道的最大沉降值位置。为进一步研究该现象,将转弯内侧超挖间隙引起的土体位移uz2(x)单独视为位移荷载施加在既有隧道上,计算不同转弯半径R0下的既有隧道沉降,如图11所示。

图11 不同转弯半径下超挖空隙引起的既有隧道沉降曲线Fig. 11 Existing tunnel settlement curves caused by overexcavation gaps with different turning radius
与图10类似,图11中超挖间隙引起的既有隧道最大沉降位置并未随转弯半径的增大而改变,均位于新旧隧道交界处左侧约3 m处。可见转弯半径的变化不会影响既有隧道沉降槽的偏移程度。
4.2 新建曲线盾构刀盘直径D′的影响
取盾构刀盘直径D′为4.28、6.28、8.28、10.28、12.28 m进行计算,既有隧道沉降计算结果如图12所示。
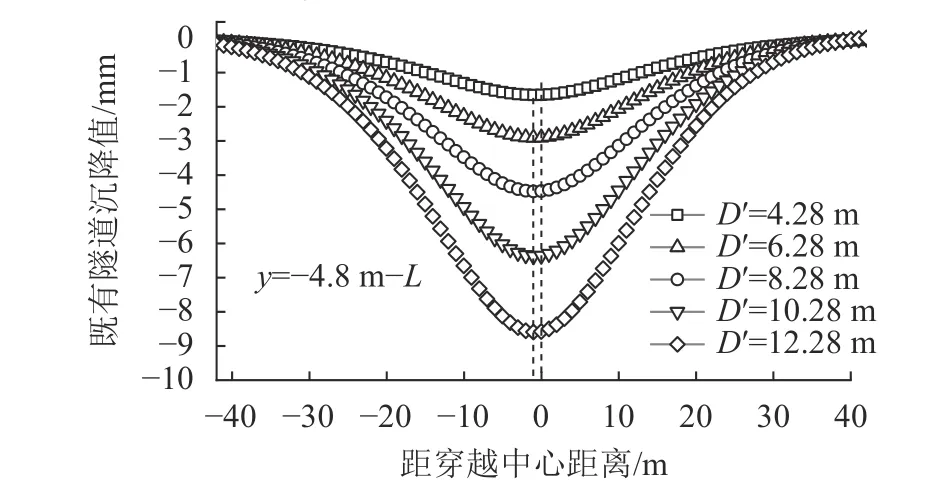
图12 不同刀盘直径下既有隧道沉降曲线Fig. 12 Existing tunnel settlement curves with different blade diameters
由图12可知:随着盾构刀盘直径D′的增加,既有隧道沉降随之增加,且增加的幅度逐渐变大。D′从10.28 m增大至12.28 m时,最大沉降值增加了34.9%;D′从10.28 m增大至12.28 m时,最大沉降值增加了34.9%;既有隧道沉降槽偏移程度变化不明显,最大沉降位置均位于新旧隧道交界处左侧1~2 m处。为此,同样对uz(x)进行拆分,将uz1(x)和uz2(x)单独视作位移荷载施加在既有隧道上,计算不同刀盘直径D′时既有隧道的沉降,如图13和14所示。
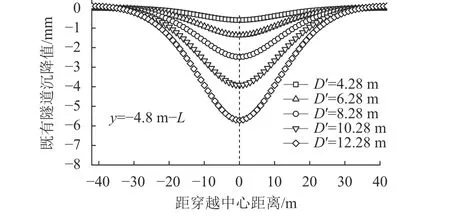
图13 不同刀盘直径下地层损失引起的既有隧道沉降曲线Fig. 13 Existing tunnel settlement curves caused by lining gap with different blade diameters
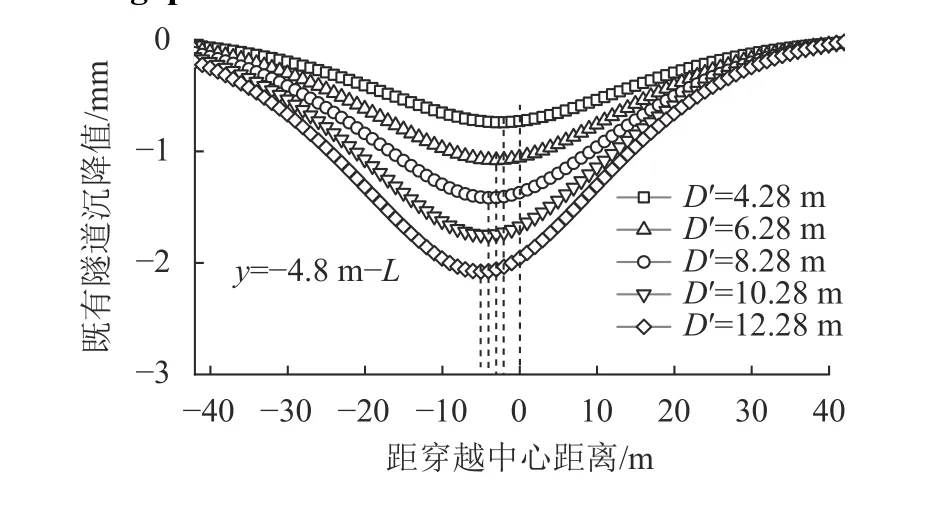
图14 不同刀盘直径下超挖间隙引起的既有隧道沉降曲线Fig. 14 Existing tunnel settlement curves caused by overexcavation gap with different blade diameters
由图13、14可知:随着刀盘直径D′的增大,由uz1(x)和uz2(x)引起的既有隧道的沉降逐渐增加,uz2的沉降槽偏移程度逐渐增大,最大沉降位置逐渐偏移至新旧隧道交界处左侧5 m处;uz2(x)引起的沉降增加幅度较小,而uz1(x)引起的沉降增加幅度较大,随着刀盘直径D′的增加,沉降值逐渐远大于uz2(x)。因此,受uz1(x)的影响,土体总沉降uz(x)引起的既有隧道沉降槽变化程度不明显。
4.3 新建隧道与既有隧道竖向间距Zc的影响
取新建隧道轴线处埋深为10 m,新建隧道与既有隧道的竖向间距Zc为0.5D、1D、1.5D、2D计算既有隧道沉降,结果如图15所示。
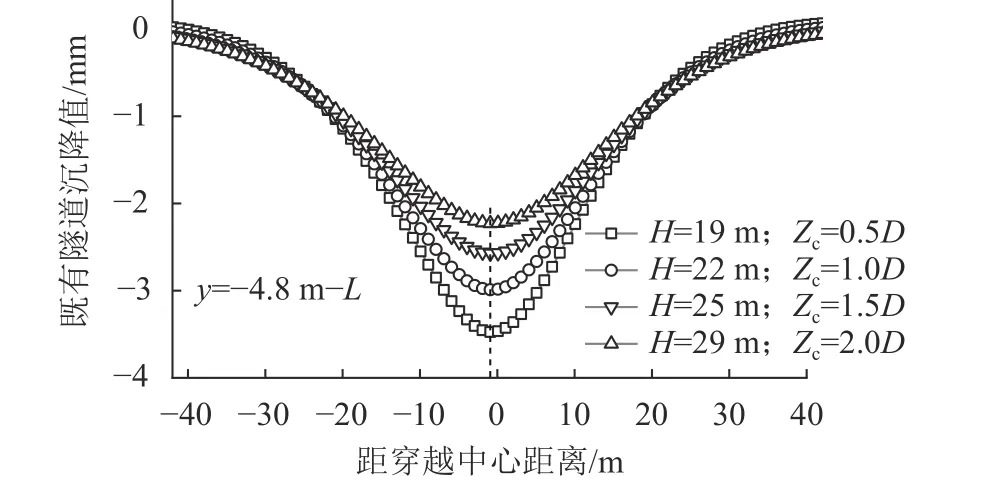
图15 不同新隧道与既有隧道竖向间距下既有隧道沉降曲线Fig. 15 Existing tunnel settlement curves with different vertical spacing between new and existing tunnels
由图15可知:随着新建隧道与既有隧道轴线之间的竖向间距Zc增大,穿越后的既有隧道的沉降逐渐减小,每增加0.5D,沉降减小约13%;此外,既有隧道沉降槽的偏移程度不受Zc的影响。
5 结 论
本文推导了新建曲线地铁盾构隧道下穿施工引起的既有隧道沉降的计算公式,并将计算结果与工程实例进行了对比,验证了公式的正确性;分析了影响既有隧道沉降的关键参数,得到如下结论:
1)受盾构转弯超挖间隙和转弯内外侧不平衡施工因素的影响,曲线地铁盾构隧道下穿施工引起的既有隧道沉降为非对称曲线,曲线盾构转弯内侧沉降大于外侧,最大沉降位置位于弯道内侧1~2 m处。
2)减小盾构转弯半径会导致既有隧道沉降增加,既有隧道弯道内侧处的沉降增速大于弯道外侧;转弯半径从300 m减小至150 m时,既有隧道沉降大幅增加;对于转弯半径小于300 m的工程应重点监测。
3)盾构转弯半径大于600 m时,既有隧道沉降与未考虑盾构曲线影响所计算的沉降相差较小,可视作直线盾构下穿施工。
4)增大盾构刀盘直径会导致下穿后的既有隧道沉降增加,且变化趋势愈发增大。既有隧道沉降槽偏移程度受盾构刀盘直径变化的影响较小,穿越后的最大沉降值位置仍位于转弯内侧1~2 m处。
5)增大新建隧道与既有隧道竖向间距会减少既有隧道沉降,每增加0.5D,沉降减少约13%。

