基于热效应的涉水混凝土工程裂缝监测方法
陈 江,熊 杰,李宇驰,熊 峰*
(1.四川大学 灾变力学与工程防灾四川省重点实验室,四川 成都 610065;2.四川大学 深地科学与工程教育部重点实验室,四川 成都 610065;3.四川大学 建筑与环境学院,四川 成都 610065)
中国正处于基础设施建设的大力发展阶段,跨江跨海大桥、港口码头、大坝、海洋平台等涉水工程在不断兴建,水下空间的开发利用也是未来缓解城市空间压力的重要举措[1]。水下混凝土工程服役环境恶劣,其建设和运营过程中的安全问题尤其突出。裂缝是混凝土最常见的缺陷,对于水下混凝土工程,裂缝不仅降低结构承载能力、刚度和耐久性,还可能导致漏水、增加钢筋锈蚀风险,其危害更加严重。尤其是处于海洋环境的钢筋混凝土结构,混凝土保护层开裂会使氯离子的侵入更容易,从而加速局部碱度损失,导致严重的钢筋腐蚀[2]。钢筋腐蚀又会加剧裂缝的发展,从而形成一个不可逆的恶性循环[3]。准确、及时地监测裂缝的发生发展过程,对保障涉水工程安全、防止事故具有重要意义。
长期以来,水下混凝土结构裂缝检测主要凭借潜水员依靠双手的触感和清水中的视觉进行辨别。20世纪80年代以来,相继出现了一系列先进的水下无损探测设备,如:水下摄像监视机[4]、超声仪[5]、图像声纳系统[6]等,但这些检测技术大多仍需要潜水员进行水下作业。水下环境复杂多变,对潜水员的生命安全有较大威胁,另外,潜水员作业时间短,难以开展长时间大面积检测任务,且潜水员下潜深度一般不宜超过50 m,难以完成深水检测任务[7–8]。随着人工智能、自动化技术的发展,各类水下机器人逐渐取代潜水员实施各种水下作业。水下机器人主要有两类:一类是有缆水下机器人,习惯上把它称为水下遥控运载体(remotely operated vehicle,ROV)[8–9];另一类是无缆水下机器人,习惯上把它称为水下自主式无人运载体(autonomous underwater vehicle,AUV)[10–11]。在水下机器人上装载封闭式水下光学相机或声纳系统对水下结构进行拍照或声纳扫描,利用深度学习算法通过计算机对图像进行处理、分析和理解[12],进而识别裂缝的方法在水下结构中得到广泛研究和应用。但是,当检测范围大且裂缝位置未知时,这种检测技术耗时较长,效率较低。同时,这种检测技术容易受到水生植物和水生动物的干扰。在流速较大、水质浑浊等恶劣水下环境中,这类检测技术也难以实施。
提前做好裂缝监测规划,在工程施工阶段将监测设施预埋在混凝土内部是一种较为保险的方案。裂缝计是工程上常用的预埋式裂缝监测仪器[13],以电阻式为主,这类监测手段历史悠久,工程经验积累较多,且被相应规范所认可,今后一定时期内仍将持续发挥作用。随着智能材料的发展,形状记忆合金[14]、光纤光栅[15]、压电陶瓷[16]等新材料在裂缝传感器研制方面也得到广泛研究。这类埋入式传感器一般只在关键部位布点,测点覆盖范围较窄,容易漏判;且传感器埋入混凝土内部,与混凝土紧密黏结,一旦损坏,无法更换,难以满足工程长期监测需求。
针对水下混凝土结构裂缝监测的技术难题,寻求新的监测途径势在必行。正如医学上将体温作为人体健康状态的重要指标一样,温度也可以反映结构物的健康状态。温度示踪法就是利用待测物理量与温度的耦合作用效应,根据待测物理量与温度的转换关系,通过可靠且费用较低的温度测量技术实现待测物理量的间接监测,该方法已在隧道火灾[17]、输油管线泄漏[18]、土体含水率[19]和渗流[20]、桩基完整性[21]等工程领域得到广泛研究和应用。事实上,水下混凝土工程处于流固耦合作用的特殊环境,热效应耦合作用是流固耦合作用的表现形式之一,本文利用这种耦合作用,提出了涉水混凝土工程裂缝监测的温度示踪法,设计了3种水下混凝土结构裂缝监测方案,通过模型试验验证了该方法用于涉水混凝土工程裂缝监测的可行性。
1 监测原理与方案
热量的传递方式包括热传导、热对流和热辐射。对于大多数传热问题,热辐射所占的比例较小,可忽略。对于混凝土这种孔隙率较小,内部无流体流动的相对密实介质,热量主要通过热传导的方式散失。根据热传导理论,单位时间从高温物体向低温物体传递的热量可表示为:

式中,qh为热流向量,λ为材料的热传导系数,T为温度,L为向量算子,D为热传导矩阵,其中,L和D的计算式为:
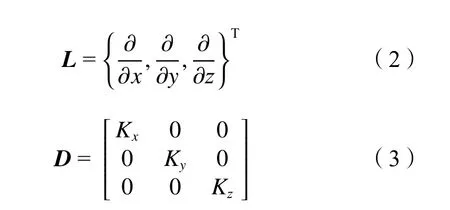
式中,Kx、Ky和Kz为3个方向的热传导系数。
当裂缝中有流体流动时,缝隙中的水流将产生对流传热效应,其热流密度可表示为:


为了使裂缝周围介质的热力学参数或传热边界条件发生变化,采用温度示踪法监测水下混凝土结构裂缝。水下混凝土结构开裂后,水渗入到裂缝中,从而使开裂部位的热力学参数发生变化,同时,在裂缝界面形成新的换热边界。但是,这种变化很微弱,除非裂缝很宽。为了提升开裂前后开裂部位热工性能的差异,提出3种监测方案如图1所示。

图1 水下混凝土结构裂缝监测方案Fig. 1 Crack monitoring scheme for underwater concrete structures
图1中,3种方案都采用耐热聚乙烯(PE–RT)或聚四氟乙烯(PTFE)材料做监测管。方案1中,套管采用脆性多孔材料,如微孔陶瓷管,当裂缝延伸至套管,由于多孔套管的毛细吸力,外界的水可沿裂缝面渗入填充套管孔隙,使套管的含水率增大,从而导致套管的热传导系数增大。方案2中:采用脆性致密材料做套管,套管的内径需比监测管外径大,使套管与监测管间有一定间隙形成空腔,用柔性密封胶封堵套管两端;开裂前,监测管–套管组件的空腔中为空气;开裂后,外界的水渗入空腔,使开裂部位周围介质发生改变,也即使热传导系数增大。由式(1)可知,热源周围介质的热传导系数增大会使热量传递速度快,从而增大热源降温速度,因此,开裂部位对应的热源降温速度明显比未开裂部位快,根据这一现象就可确定开裂信息。方案3中:灌水管与监测管并排布置,灌水管同样采用脆性致密材料;当某处产生裂缝时,外界的水将渗入灌水管,因此,当发现灌水管中有水时,即预示该条监测线路上有裂缝;此时,可将灌水管与恒水位水箱相连,由于水压差,灌水管中的水将通过裂缝流入外界,从而在裂缝界面产生对流传热效应,裂缝附近热源的降温速度将明显变快,根据这一现象即可确定开裂信息。
陈江等[20]定义了反映降温速度的判别指标ξv,如式(5)所示:
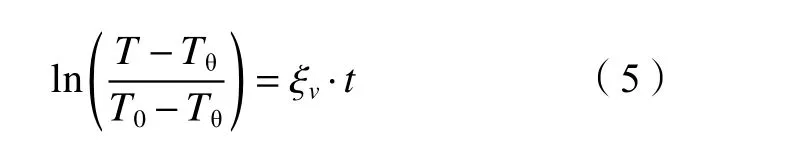
式中,T0为降温初始温度,Tθ为环境温度。
选取ln(T–Tθ)时程曲线中线性度较好的时段进行线性拟合,拟合直线的斜率即为ξv。利用t1~tn时段测试的温度计算ξv:
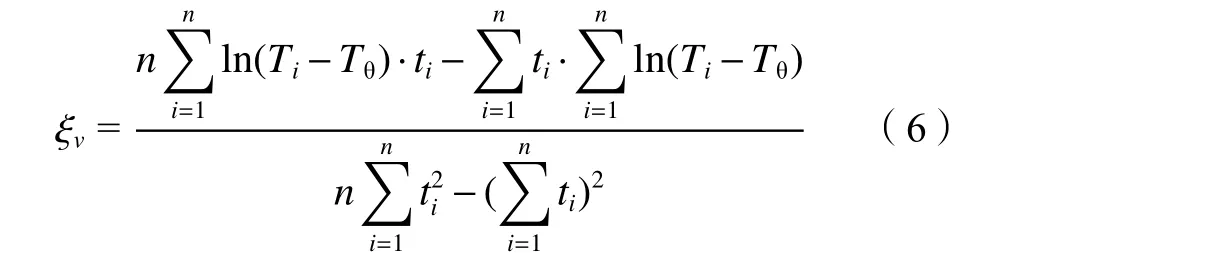
式中,Ti为ti时刻的温度。
2 试 验
2.1 试件
测试试件采用钢筋混凝土梁,试件截面尺寸为150 mm×150 mm,长550 mm,按图1所示的监测方案分别在混凝土内部预埋监测管–套管组件或监测管–灌水管组件,如图2所示。图2中,监测管选用耐热聚乙烯(PE–RT)管,其外径和壁厚分别为20和2 mm。方案1中,微孔陶瓷管的内径为20 mm,外径为40 mm,长为100 mm,其微孔尺寸为70 µm,孔隙率为0.35;方案2中,陶瓷管的内径为25 mm,外径为35 mm,长为200 mm;方案3中,灌水管采用外径为18 mm,壁厚为2 mm的陶瓷管。

图2 试件制作Fig. 2 Specimen fabrication
2.2 测试装置
采用陶瓷加热管模拟图1中的点热源,采用光纤光栅温度传感器测量点热源的温度时程响应,采用导热胶把光纤光栅温度传感器与陶瓷加热管集成于一体,其结构如图3所示。
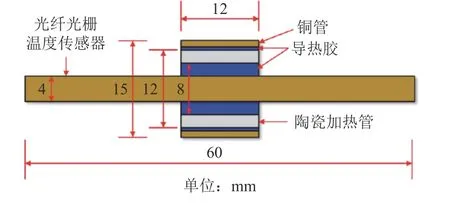
图3 传感加热单元结构示意图Fig. 3 Sketch map of sensing-heating element
图3中,采用外径4 mm,长60 mm的铜管封装光纤光栅温度传感器;陶瓷加热管的外径、内径和长度分别为12、8和12 mm。为了减小传感加热单元与监测管内壁的间隙,用1根外径15 mm,壁厚1 mm的铜管套在陶瓷加热管外。采用聚华公司生产的JH–FBG–C1型解调仪测试光纤光栅温度传感器的波长,其波长测试范围为1 528~1 568 nm,采样频率最高可达1 000 Hz,波长分辨率为0.1 pm,波长测量精度为±0.5 pm,动态范围大于25 dB。
2.3 试验结果
2.3.1 方案1
设环境温度下光纤光栅温度传感器的中心波长为λθ,由于光纤光栅的波长λ与温度呈线性关系,因此,ln(λ–λθ)时程曲线的特征与ln(T–Tθ)时程曲线相似。开裂前后测点的ln(λ–λθ)时程曲线如图4所示。由图4可以看出:ln(λ–λθ)时程曲线的斜率均具有前期较大,后期较小的特征,这主要是由于前期温度梯度大,散热快所致。由于混凝土的孔隙率较小,几乎不渗水,监测管周围介质的热力学参数在浸水前后基本相同。因此,当混凝土未开裂时,是否浸水对热源降温规律几乎没有影响,ln(λ–λθ)时程曲线基本一致。当混凝土开裂后,由于微孔陶瓷管的吸水作用,裂缝面浸水导致监测管周围介质的热力学参数改变幅度较大,开裂前后,ln(λ–λθ)时程曲线有较明显的区别。选取20~200 s 时段的波长监测数据,计算3种状态对应的降温速度判别指标分别为–7.806×10–3、–7.972×10–3和–10.268×10–3,可见开裂后测点降温速度判别指标的绝对值明显增大。根据这一异常现象可进行开裂部位的识别,但这种方案难于识别裂缝宽度。
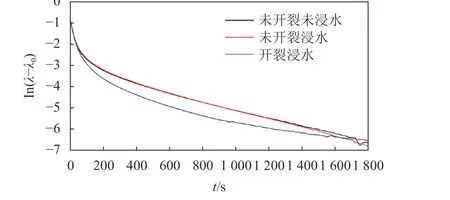
图4 ln(λ–λθ)时程曲线对比(方案1)Fig. 4 Comparison of the time-history curves of ln(λ–λθ)with scheme 1
2.3.2 方案2
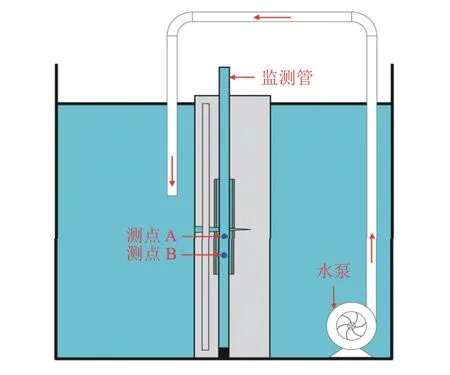
图5 方案2试验装置Fig. 5 Sketch map of test setup for the second scheme
当试件在静水中时,不同裂缝宽度w对应的测点降温阶段的ln(λ–λθ)时程曲线如图6所示。由图6可以看出,测点A和测点B的ln(λ–λθ)时程曲线开裂后与开裂前相比存在明显变化,但不同裂缝宽度对应的ln(λ–λθ)时程曲线差异较小。

图6 静水中ln(λ−λθ)时程曲线对比(方案2)Fig. 6 Comparison of the time-history curves of ln(λ−λθ) in still water with monitoring scheme 2
取t1= 0,tn= 80 s,采用式(6)计算静水环境中不同裂缝宽度对应的ln(λ–λθ)时程曲线的初始斜率ξi,见表1。
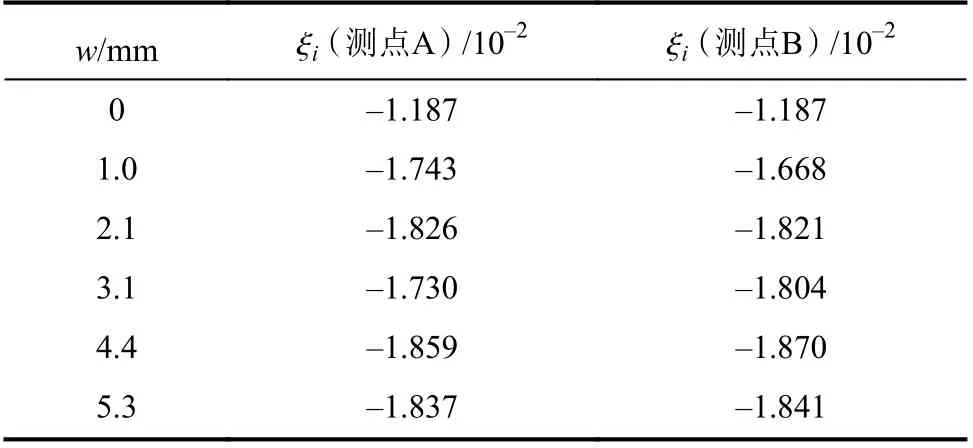
表1 静水中 ξi的计算结果Tab. 1 Calculation results of ξi in still water
由表1可见:开裂后ξi的绝对值明显大于开裂前ξi的绝对值;在不同裂缝宽度下,两个测点降温阶段的ln(λ–λθ)时程曲线基本一致,ξi值也基本相同,说明在静水环境中,采用方案2只能判别套管覆盖面内是否开裂,而无法识别裂缝宽度。
启动水泵,使水箱中的水产生循环流动来模拟流动水环境。当水泵流量为18 500 mL·min–1时,不同裂缝宽度对应的测点降温阶段ln(λ–λθ)时程曲线如图7所示。由图7可以看出:在流动水环境中,测点A降温阶段的ln(λ–λθ)时程曲线与裂缝宽度相关;测点B降温阶段的ln(λ–λθ)时程曲线受裂缝宽度的影响较小。
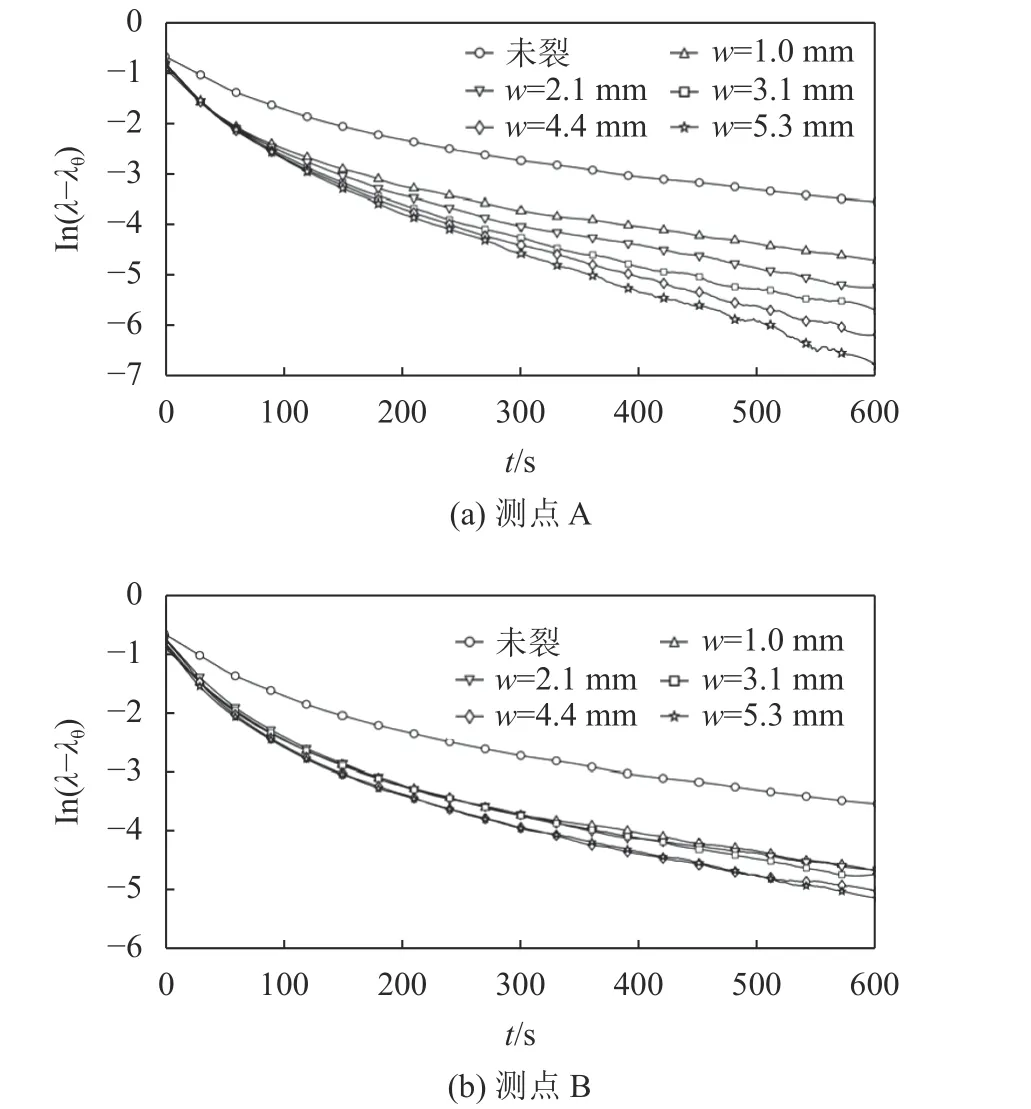
图7 动水中ln(λ–λθ)时程曲线对(方案2)Fig. 7 Comparison of the time-history curves of ln(λ–λθ) in flowing water with monitoring scheme 2
取t1= 0,tn= 80 s,采用式(6)计算流动水环境中不同裂缝宽度对应的ln(λ–λθ)时程曲线的初始斜率ξi见表2。取t1= 200 s,tn= 500 s,采用式(6)计算流动水环境中不同裂缝宽度对应的ln(λ–λθ)时程曲线的后期斜率ξj见表3。

表2 流动水环境中 ξi的计算结果Tab. 2 Calculation results of ξi in flowing water

表3 流动水环境中 ξj的计算结果Tab. 3 Calculation results of ξj in flowing water
由表2、3可见:测点A降温阶段,ln(λ–λθ)时程曲线的初始斜率绝对值基本上随裂缝宽度的增大而增大,但增大的趋势不明显;而后期斜率的绝对值随裂缝宽度增大而增大的趋势则较明显。测点B降温阶段ln(λ–λθ)时程曲线的初始斜率只与是否开裂有关,与裂缝宽度基本无关;其后期斜率的绝对值基本上随裂缝宽度的增大而增大,但变化幅度不大。
后期斜率ξj与裂缝宽度w的关系如图8所示。在测试的裂缝宽度范围内, ξj与w的拟合关系可表示为:
田光居“上馆”三月,在了解太子丹意图及其门客的才能之后,以“欲为太子良谋,则太子不能;欲奋筋力,则臣不能”的两难,向太子推荐了“神勇之人”荆轲。事后,却因太子送别之时的一句叮嘱“此国事,愿勿泄之”而在荆轲面前“吞舌而死”,既以保全“不为人所疑”之节操,亦借此激励荆轲。
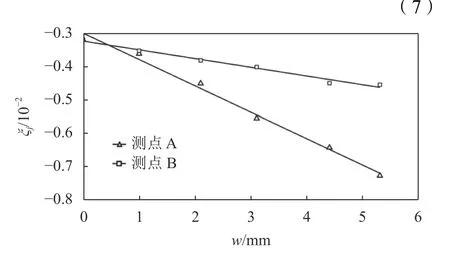
图8 ξj与w拟合关系Fig. 8 Fitting relationship between ξj and w width

综上,在流动水环境中,采用方案2可识别裂缝宽度,测点离裂缝越近,后期斜率对裂缝宽度越敏感。
2.3.3 方案3
在静水环境中,对不同裂缝宽度和渗漏流量的组合工况开展如图9所示部位的测试。
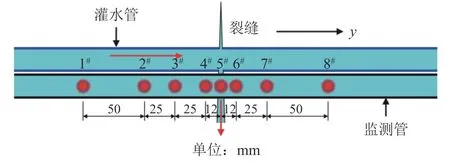
图9 测点布置Fig. 9 Layout of measuring points
定义无量纲参数Γ为:

式中,λ0为降温初始时刻光纤光栅温度传感器的中心波长。
在半对数坐标轴中绘制降温阶段各测点的Γ时程曲线,作为示例,图10给出了当裂缝宽度为0.6 mm,渗漏流量qw为100 mL·min−1时,图9所示的各测点对应的Γ时程曲线,其他工况的Γ时程曲线的变化规律与之类似。由图10可以看出:当150 s≤t≤600 s时,lg Γ的时程曲线具有线性特征,该时段时程曲线的斜率与热源降温速度具有很好的相关性。测点离裂缝越近,其对应的时程曲线在该时段的斜率的绝对值也越大,因此,后续分析统一将150 s≤t≤600 s时段,lg Γ时程曲线的斜率作为裂缝判别指标ψ。
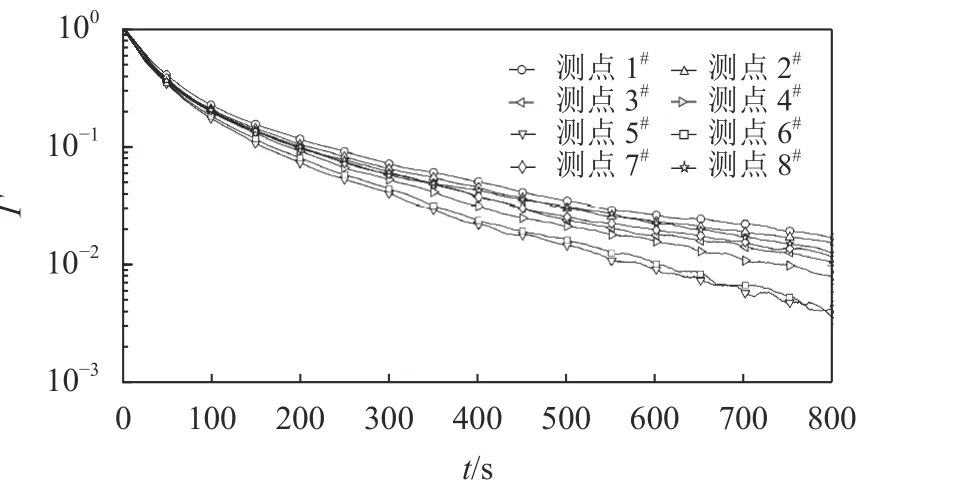
图10 Γ时程曲线的半对数坐标图Fig. 10 Semilogarithmic plot of time-history curves of Γ
当裂缝宽度w为0.4 mm时,图9所示各测点ψ值的分布特征如图11所示(裂缝所在位置的y坐标设为0)。在未开裂状态下,在灌水管中灌满水,测得的ψ值为–1.606×10–3,图11中,虚线即为ψ=–1.606×10–3的基准线。
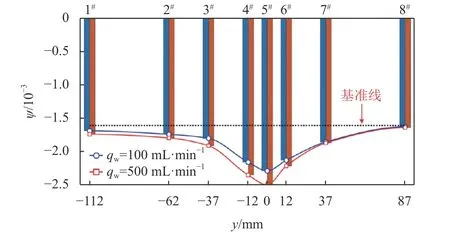
图11 w=0.4 mm时ψ的分布特征Fig. 11 Distribution of ψ under different leakage flow when w = 0.4 mm
由图11可以看出:离裂缝越近,ψ的绝对值越大,其分布特征能很好地反映裂缝的位置;当裂缝宽度一定时,渗漏流量越大,缝隙中的流速越大,ψ的绝对值也越大;裂缝下端灌水管中的流速接近0,因此,位于裂缝下端的测点(测点6#~8#)的降温规律主要受缝隙中流速的影响,测点离裂缝越远,其所受影响越小,如:测点8#的ψ值与未开裂状态下的ψ值基本相同,说明测点8#的降温规律基本不受裂缝中流速的影响;裂缝上端灌水管中的流速与渗漏流量成正比,位于裂缝上端测点(测点1#~4#)的降温规律除了受缝隙中流速的影响外,还会受灌水管中流速的影响,因此,与测点8#相比,测点1#虽然距裂缝更远,但ψ的绝对值更大,且测点1#的ψ的绝对值随渗漏流量的增大呈增大趋势。
当裂缝宽度一定时,渗漏流量越大,缝隙中的流速越大,对流传热效应越显著,热源降温越快。在半对数坐标轴中绘制不同裂缝宽度和渗漏流量的组合工况下,测点5#的ψ值与qw的关系曲线如图12所示。由图12可以看出,当裂缝宽度一定时,随着渗漏流量的增大,ψ的绝对值呈增大趋势,其增大的幅度在变缓,说明渗漏流量越大,开裂部位ψ的绝对值与未开裂部位的差异越大,监测效果更佳。
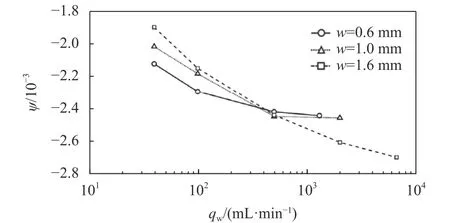
图12 测点5#的ψ值与qw的关系曲线Fig. 12 Relationship between qw and ψ for test point 5#
随着裂缝宽度的增大,缝隙处的抗渗性降低,在水头差一定时,渗漏流量越大。图13绘制了当水头差为88 cm时,渗漏流量与裂缝宽度的关系曲线。

图13 qw与w的关系Fig. 13 Relationship between qw and w
由图13可以看出:随着裂缝宽度的增大,渗漏流量具有非常明显的递增趋势,在测试的裂缝宽度范围内,二者的拟合关系见式(9),因此,ψ可作为裂缝定位的判别指标,渗漏流量可用于裂缝宽度的识别。

3 结 论
本文基于流体–热源–裂缝的热效应耦合作用,提出了涉水混凝土工程裂缝监测的温度示踪法,并设计了3种裂缝监测方案,针对这3种监测方案,分别开展了裂缝监测模型试验,根据试验结果,可得到以下结论:1)根据热源降温规律,这3种方案均能较好地识别是否有裂缝产生。在裂缝定位方面,方案1和方案2只能判断套管覆盖范围内是否有裂缝;方案3的裂缝定位精度更高,但需要布置更多测点。2)在静水环境中,方案1和方案2均不能识别裂缝宽度;在流动水环境中,方案2可识别裂缝宽度,且测点离裂缝越近,灵敏度越高。3)在静水环境中,采用方案3监测裂缝时,渗漏流量与水头压力和裂缝宽度有关,当水头压力一定时,可根据渗漏流量与裂缝宽度的关系识别裂缝宽度。

