正交胶合木环型耗能节点设计与抗剪试验研究

薛素铎，赵艳阳，沈银澜，武旺琪，郭汉桢

(北京工业大学 城市建设学部，北京 100124)

正交胶合木（cross-laminated timber，CLT）是通过3层以上的锯材正交组坯胶合挤压成的现代工程木产品，具有装配化程度高、保温隔热性能好、绿色环保、木材利用率高与抗震性能好等优点，适合作为装配式与多高层的木结构建筑用材，是打造绿色生态、宜居美丽的乡村装配式多高层建筑的重要绿色建材。由于这种交错层压的设计，正交胶合木产品平面内与平面外均具有较高的强度与刚度，且具有稳定的形状尺寸。连接节点对正交胶合木墙体抗侧力机制的发挥及延性和耗能起着至关重要的作用。

早期，Ceccotti[1]、Dujič[2]及Popovski[3]等学者对不同锚固连接的CLT剪力墙进行了拟静力试验，发现加载过程中CLT墙板表现出刚体旋转，连接节点产生变形与耗散能量。大量学者开展了正交胶合木常规标准连接节点的研究。Schneider[4]、Shen[5]、沈银澜[6]等开展了标准角钢节点试验工作及损伤分析研究，Shen等[7]也第一次将OpenSees软件中的Pinching4自定义本构模型引到正交胶合木节点，准确量化其滞回曲线的强度、刚度退化及捏拢效应，将节点等效成两个正交弹簧模拟正交胶合木墙体的抗侧力性能。Rey[8]、Sun[9]等对标准连接件连接进行改进，开展相关研究工作，并对多高层CLT结构进行数值模拟研究。Gavric[10–11]等对传统标准角钢连接节点进行了试验研究及理论计算，发现理论公式过高或过低估测其抗侧刚度及承载能力，强调开展试验校正的必要性。常规的标准角钢连接节点需通过开展试验评估其承载力，且耗能能力有限，往往发生不可控的脆性或延性破坏，并伴随节点区木材的劈裂或损坏，从而导致其剪力墙优势不能充分发挥，且不可更换修复，成本也较高。为此，近年来的研究方向开始注重于正交胶合木新型耗能节点的研发。Polastri等[12–13]提出X-rad连接方式，以连接地震地区的大型CLT板。Hossain等[14]研究了双角全螺纹螺钉的面板–面板接头。Latour等[15]采用一种锚固翼缘为沙漏形状的连接角钢保证紧固件不先于连接件破坏。Schneider等[16]引入薄壁钢管连接提供较高的承载力，还能有效防止木材的破坏。另有学者们提出了用于CLT墙板之间拼接的X-bracket耗能节点[17]、UFP连接[18–19]、O连接[20]与滑动摩擦连接[21–22]。Ding等[23–24]提出DfD连接用于改善再生混凝土剪力墙的裂缝和破坏形式及混凝土梁柱节点的抗震性能。

U型阻尼器取材方便、构造简单、易于设计、成本较低，是第一代金属阻尼器的典型代表[25]。本文提出一种通过成本较低的Q235钢板加工而成的U型阻尼器拼装成环形连接节点，将正交胶合木连接于基础钢梁，将正交胶合木墙体损伤集中于耗能构件，通过合理设计使得钢木连接实现可更换。本文设计不同厚度、不同平直段宽度的试件共计7个，开展低周往复的抗剪性能试验，分析其破坏机理、滞回性能、承载力退化、刚度退化性能及耗能能力等性能，结合Eurocode 5[26]等标准理论计算正交胶合木锚固端抗剪承载力，推导耗能节点的主要抗剪力学性能指标的计算公式，并基于有限元软件Abaqus开展数值模拟，以期为正交胶合木结构耗能节点的设计及应用提供依据。

1 耗能节点设计

耗能钢木连接节点由正交胶合木（CLT）试块、钢板、环型阻尼器及H型钢框架4部分组成，如图1所示。

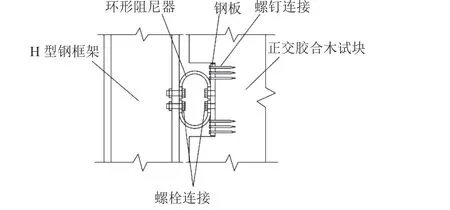
图1 耗能钢木连接节点示意图Fig. 1 Schematic diagram of dissipative connector for CLT structure

图1中：由两个U型阻尼器拼接成1个环形连接节点，U型阻尼器由Q235钢板切割弯曲制作成型，其构造包括圆弧段、平直段及收腰平直段3部分，上、下平直段均开设4个螺栓孔，一端与钢梁进行螺栓连接，另一端与固定在正交胶合木试块端面的钢板进行螺栓连接；钢板与正交胶合木横截面通过足量的螺钉连接，以保证较强的连接端，从而将节点这个薄弱构件转换为可更换的双U型钢板，通过有效平直段与环形耗能段提供节点的变形与耗能。

2 试件设计及材性测试

2.1 试件设计

试验共设计7对U型阻尼器试件，其编号分别为D4–S50、D4–S60、D6–S86、D6–S50、D6–S60、D8–S86、D8–S55。其中，D后的数字表示厚度，分别为4、6、8 mm 3种，S后的数字表示平直段有效宽度，分为全尺寸与收腰2种类型。所有试件圆弧处外径均相同，收腰处倒5 mm的直角，几何尺寸见表1。阻尼器一端与钢框架（型号为H200×200×10×10）通过开设的4个M14的螺栓孔连接，另外一端与通过自攻螺钉锚固在正交胶合木10 mm厚的Q355钢板连接；该钢板上开设4个M14螺栓孔，并开设18个直径为5 mm的自攻螺钉孔，螺钉型号为rothoblaas的LBS5x70 mm；耗能连接几何尺寸构造如图2所示。

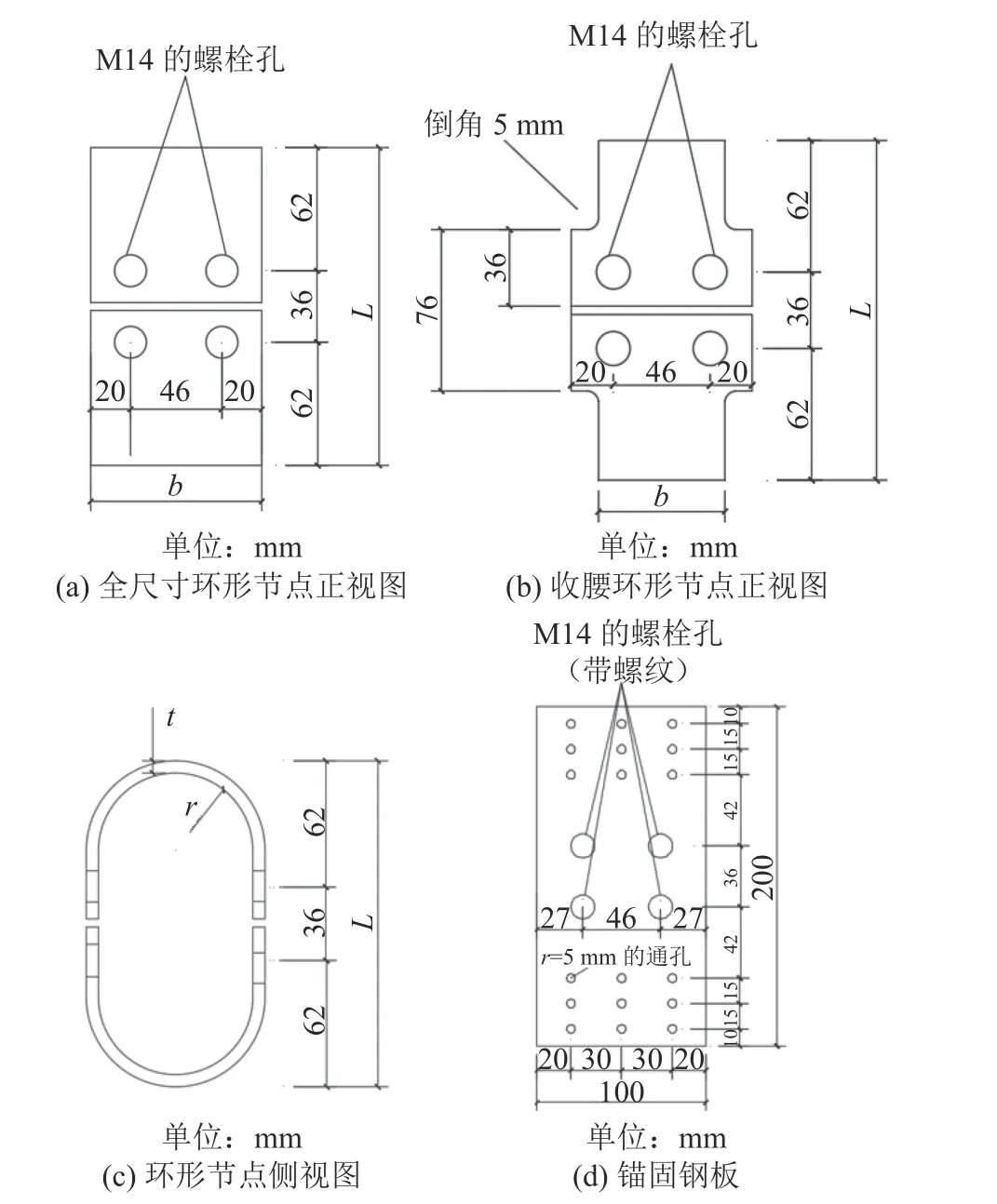
图2 耗能连接几何尺寸构造Fig. 2 Geometrical dimension construction of dissipative connections

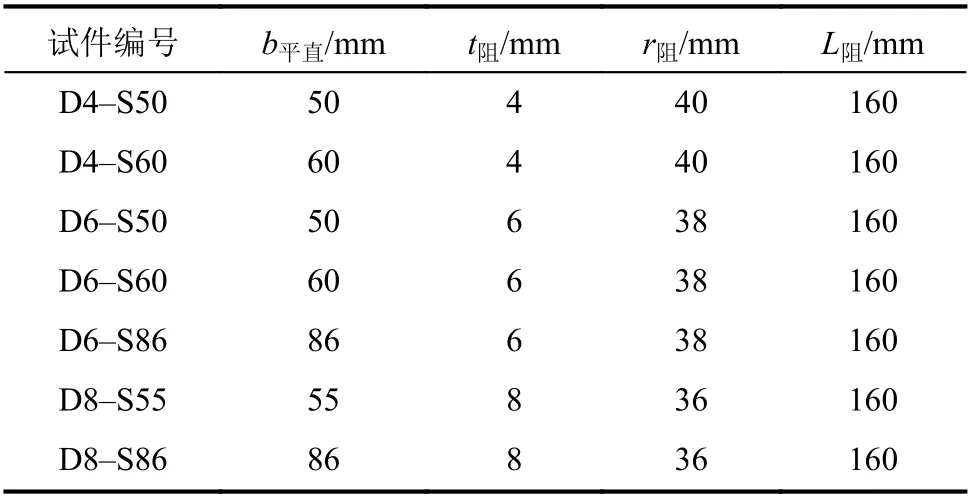
表1 试件相关尺寸Tab. 1 Dimensional parameters of specimens

2.2 材性测试

环形阻尼器试件是由Q235钢板切割弯曲制作而成，其钢板厚度分别为4、6、8 mm。根据《金属材料拉伸试验第1部分：室温试验方法》（GB/T 228.1—2010），在北京工业大学工程力学国家重点实验室，使用最大负荷为100 kN的微机控制电子万能试验机（Z100），对3种钢板厚度的试件开展抗拉材性测试，试验结果见表2。105 mm 3层SPF正交胶合木（CLT）满足E1级，其材料性能见表3。

表2 Q235 钢板材料力学性能Tab. 2 Mechanical properties of steel plate materials

表3 105 mm 3层SPF正交胶合木（CLT）材料力学性能Tab. 3 Mechanical properties of 105 mm thick three-layer SPF cross-laminated timber (CLT) material

2.3 试验加载装置设计及加载方案

设计一套正交胶合木–基础钢梁的耗能连接节点抗剪试验加载装置，如图3所示。图3中：正交胶合木试块尺寸为350 mm ×180 mm×105 mm，在一侧开设220 mm×80 mm×105 mm的凹槽，用于连接放置环形阻尼器与连接钢板，凹槽也起到阻尼器变形限位作用；正交胶合木试块采用上下30 mm厚度的钢板，压紧固定4根M12长螺栓杆，上部盖板开设直径为30 mm的圆孔，与试验机加载头连接；加载过程中，为防止正交胶合木试块在上下钢盖板之间滑移，采用螺钉固定正交胶合木上下端与相应的上下盖板。采用顶部覆盖30 mm厚的钢板与M12长螺栓杆把H型钢梁压在试验机地梁上（通过螺栓与滑槽内的滑动块进行连接）；为防止H钢梁的侧向滑动，采用三角钢架顶紧外侧翼缘；在对侧，为防止加载过程中正交胶合木试件连带上下盖板对加载头造成弯扭，在正交胶合木试件的下盖板竖直滑动范围内顶紧另一三角钢架。

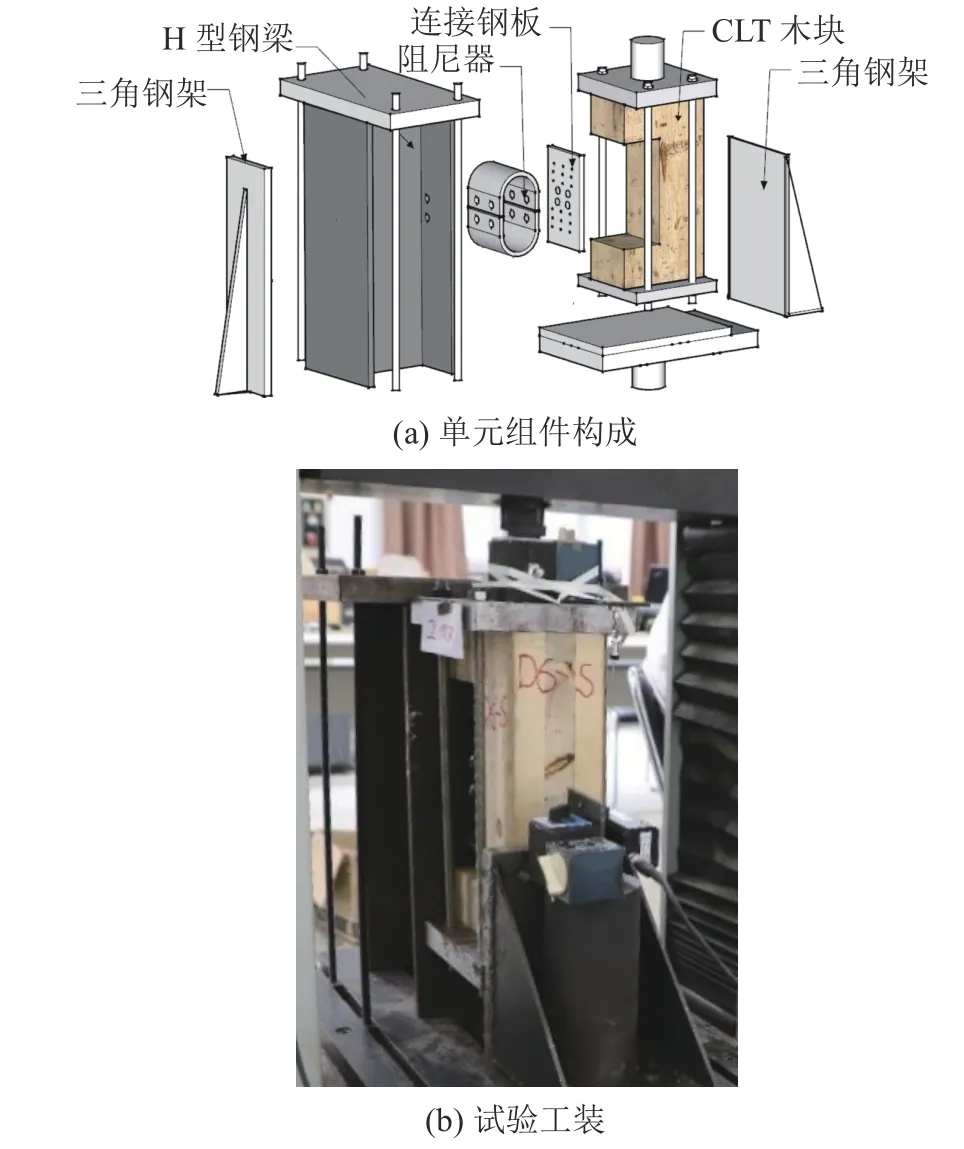
图3 加载装置图Fig. 3 Loading device diagram

试验在北京工业大学工程力学国家重点实验室进行，使用QBD–100测试设备对试件进行低周往复加载试验。根据电子万能压缩试验程序100 kN（V601）对上部横梁施加拉压荷载，进行位移控制的低周往复试验。通过加载头上的传感器获得力，通过拉线位移计测得节点的变形。其加载制度如图4所示。第1级与第2级加载位移分别为2、5 mm，每级加载循环3次；当位移加载至10 mm时，每级加载等级的幅值增加5 mm，每个等级下位移循环加载3次，最大加载位移控制在60 mm范围内（考虑正交胶合木凹槽对环形阻尼器变形限位或试件出现裂纹）。

图4 试验加载制度Fig. 4 Loading protocol

3 试验结果与分析

3.1 试验现象与破坏形态

在试验过程中，共发生3种破坏模式：1）螺栓螺纹破坏及锚固端钢板弯曲。试件D8–S86在位移幅值加载至40 mm时，连接锚固端螺栓螺纹发生破坏，连接正交胶合木端面的钢板中间部分有所弯曲，如图5（a）所示。2）阻尼器收腰处出现裂缝。试件D8–S55加载至40 mm，D6–S50、D6–S60加载至50 mm时，阻尼器圆弧与平直段连接处出现3～4 mm裂痕，如图5（b）所示。这是由于收腰采用直角倒角过度，且平直段产生主要耗能作用，引起偏厚的钢板该处的应力集中，导致收腰开始位置的裂纹。因此，在后期阻尼器的设计中建议采用圆弧倒角过度。3）阻尼器出现较大变形，被正交胶合木凹槽限位顶住。试件D6–S86、D4–S50、D4–S60均在位移幅值加载至50～60 mm时，阻尼器的平直段除锚固段外已经全部变形，试件圆弧处与正交胶合木凹槽接触，如图5（c）所示。从试验现象可以看出，钢板厚度越薄，平直段收腰越少，阻尼器越不容易被破坏，同时变形能力越好。

图5 破坏模式Fig. 5 Failure mode

3.2 滞回性能

为调查和量化不同设计参数对试件抗剪性能的影响，图6给出所有节点的骨架曲线，本文规定拉方向位移与力均为正向。各试件的初始刚度、屈服力、屈服位移等参数见表4，本文重点讨论收腰宽度及厚度对节点各参数的影响。

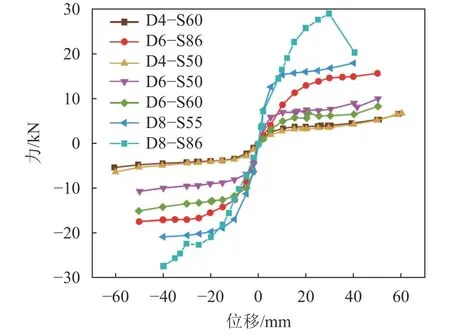
图6 骨架曲线Fig. 6 Skeleton curves

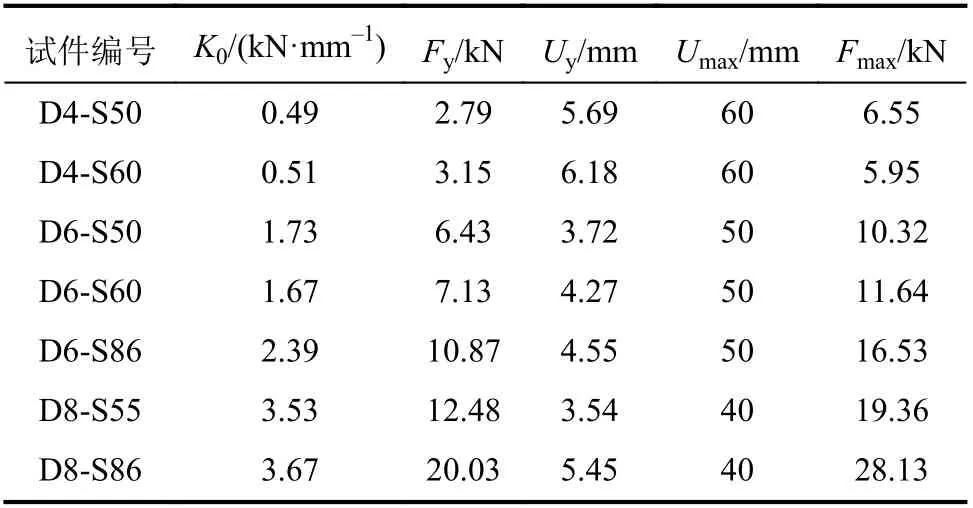
表4 环形耗能节点试验结果Tab. 4 Experimental results of annular dissipative connectors

3.2.1 平直段收腰宽度对滞回性能影响

图7给出厚度为8 mm的试件D8–S55和D8–S86及厚度为6 mm的试件D6–S86、D6–S60与D6–S50不同收腰对节点滞回性能的影响。

由图7（a）可知：试件D8–S86滞回曲线呈现严重捏拢，表明存在节点的松动和滑移，是锚固端与阻尼器共同作用结果；D8–S55试件滞回曲线呈饱满的梭形，且承载力退化小，表明耗能节点实现了将损伤集中于阻尼器上。8 mm厚的环形阻尼器由86 mm收腰到55 mm，屈服荷载下降了60.50%（20.03 kN下降到12.48 kN），最大抗剪承载力下降45.30%（28.13 kN 下降到19.36 kN）。由图7（b）发现6 mm厚的环形阻尼器系列滞回曲线饱满稳定，将耗能集中于阻尼器上，由86 mm收腰到60 mm，屈服荷载下降了52.45%（10.87 kN下降到7.13 kN），最终承载力下降幅度接近42.01%（16.53 kN下降到11.64 kN），抗侧刚度减少43.11%（2.39 kN/mm下降到1.67 kN/mm），由60 mm收腰到50 mm，承载力与屈服荷载略有所下降。

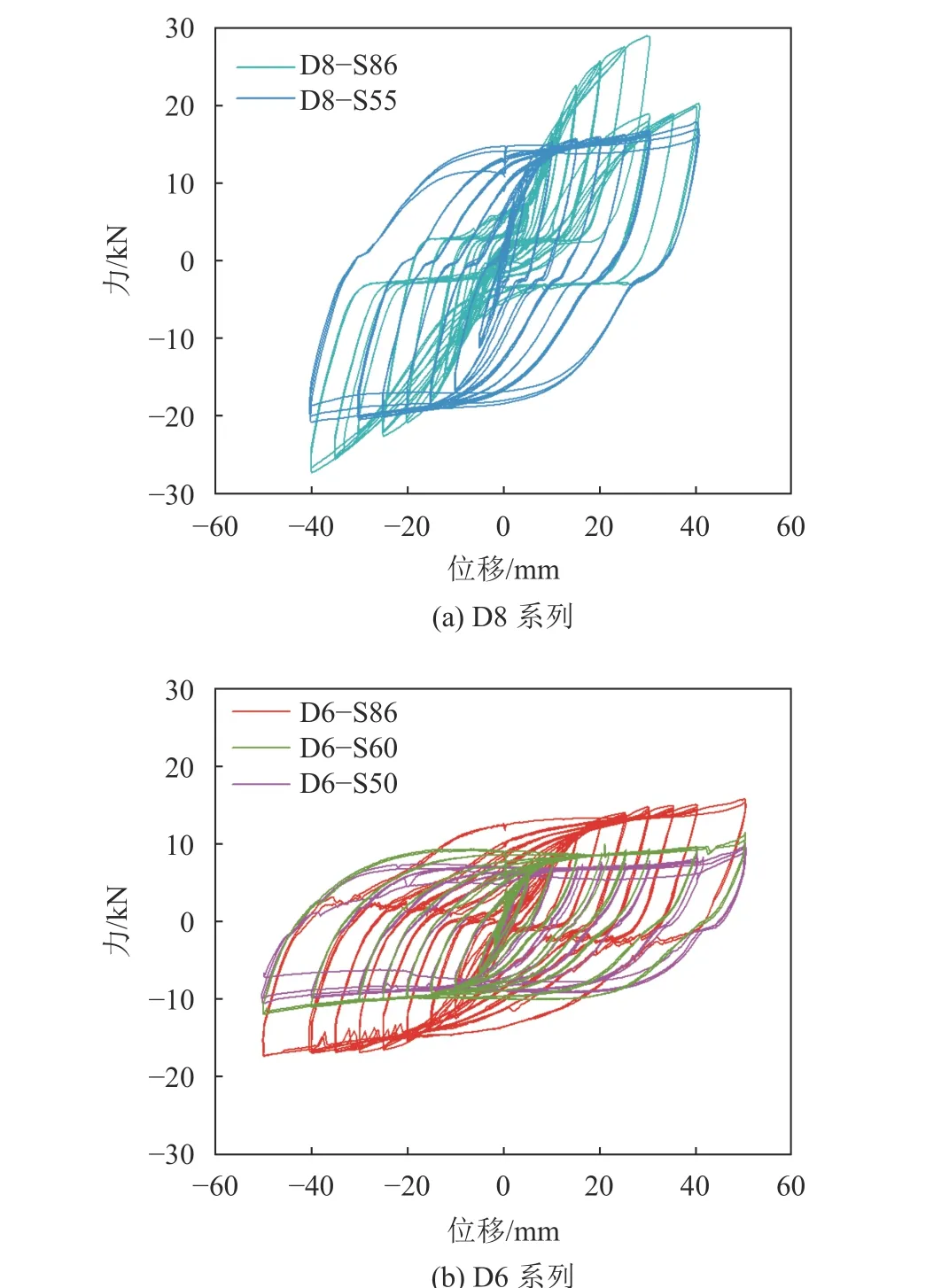
图7 不同收腰宽度下滞回曲线对比Fig. 7 Comparison of hysteretic curves with different waist widths of steel plates

3.2.2 厚度对滞回性能影响

不同厚度对节点滞回性能的影响如图8所示。

由图8（a）可知：由于厚度为8 mm的阻尼器强度过大，滞回环出现“捏拢”现象，阻尼器未展现良好耗能效果；在厚度减为6 mm时，其滞回曲线成饱满的梭形，抗侧刚度从3.67 kN/mm降至2.39 kN/mm，下降了53.56%；承载力从28.13 kN降至16.53 kN，下降了70.18%。由图8（b）可知：两个阻尼器滞回环均稳定饱满，厚度为6 mm的阻尼器由于具有更大的抗侧刚度，比4 mm厚度的试件承载力能力较强；厚度由6 mm降低至4 mm时，抗侧刚度从1.67 kN/mm降至0.51 kN/mm，下降了227.45%，其承载力从11.64 kN降至5.95 kN，降低了约95.63%。

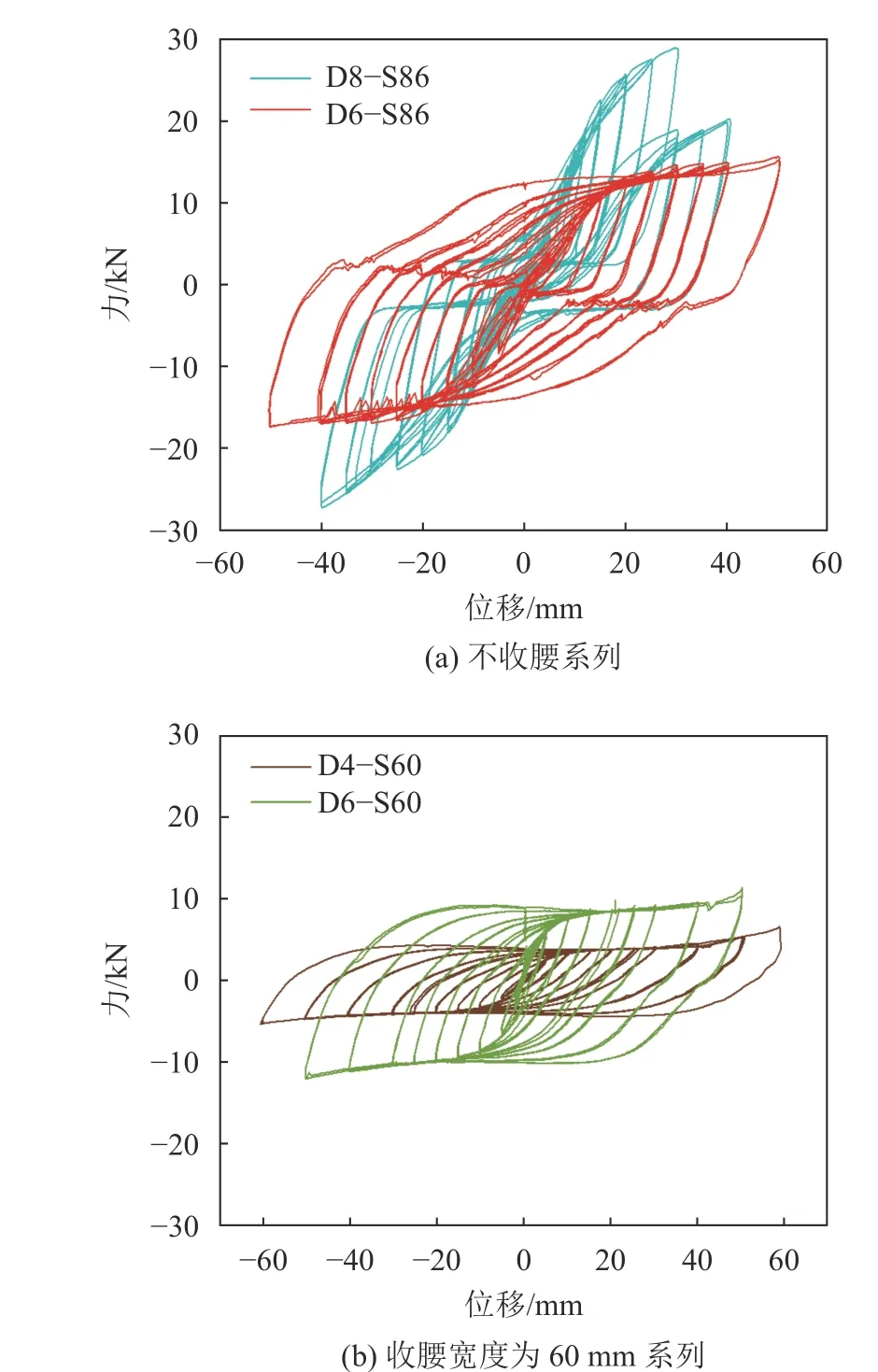
图8 不同钢板厚度情况下滞回曲线对比Fig. 8 Comparison of hysteretic curves with different thickness of steel plates

结合试验现象及滞回曲线分析发现，除D8–S86以外，大部分试件环形阻尼器集中耗能，损伤发生于耗能连接件上，保证锚固端的强连接。因此，下面将对除D8–S86以外的试件耗能连接节点的力学性能进行讨论。

3.3 承载力退化行为

抗剪试验中，每级加载循环均为3次，用每级加载的第3次循环的最大荷载与第1次循环的最大荷载的比值评估试件的承载力退化率，承载力退化曲线如图9所示。

图9 承载力退化曲线Fig. 9 Bearing capacity degradation curves

由图9可见：各试件的承载退化率在0.8～1.1之间；在各试件破坏之前，各试件承载力退化很小，证明此新型阻尼器具有较好的承载能力。其中部分承载力退化率大于1，是由于钢板在低周往复加载作用下产生强化作用，导致在部分位移下第3次循环的最大荷载大于第1次循环的最大荷载。

3.4 刚度退化行为

在循环往复荷载作用下，采用等效割线刚度[27]K的变化来评估耗能节点的刚度退化行为，各节点的刚度退化曲线如图10所示。由图10可见：各试件的刚度退化过程都较为相似，刚度由陡到缓，逐渐下降，初始刚度退化较快。试件D8–S55明显高于D6系列（D6–S60和D6–S50）的刚度退化，D4系列（D4–S50和D4–S60）刚度退化最小；阻尼器钢板厚度对刚度退化影响较大，厚度越大，试件的抗侧刚度越大，但刚度退化也快。当加载位移在20 mm之内，D8–S55抗侧刚度在3.53～0.89 kN/mm内急剧下降，但在相同位移下，D8–S55与D6–S86相比，其抗侧刚度下降不低于1.26倍。当位移大于20 mm时，刚度退化程度明显变缓，D8–S55抗侧刚度由0.86 退化至0.48 kN/mm；D6–S86抗侧刚度由0.70 降至0.33 kN/mm；D6–S60、D6–S50、D4–S60和D4–S50的变化更为平缓。

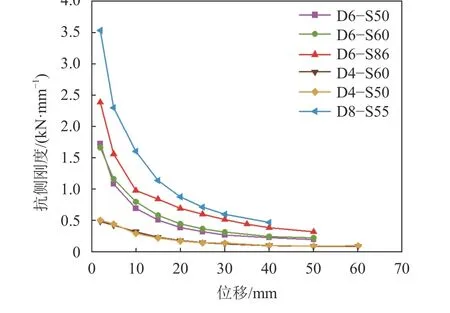
图10 刚度退化曲线Fig. 10 Stiffness degradation curves

3.5 耗能性能评价

采用等效黏滞阻尼系数和累计耗能量评估试件的耗能能力。通过积分计算各试件的等效黏滞阻尼系数，其结果如图11所示。由图11可见：D6–S86的等效黏滞阻尼系数明显低于其他耗能节点，这可能是由于其他节点收腰导致黏滞阻尼系数的提高；其他节点等效黏滞阻尼系数曲线接近。当加载位移小于25 mm时，所有试件的等效黏滞阻尼系数增长较快，等效黏滞阻尼系数达到0.3以上；当加载位移超过25 mm时，所有试件的等效黏滞阻尼系数增长速度变缓；当加载位移到40 mm时，达到0.4以上。

图11 等效黏滞阻尼系数曲线Fig. 11 Equivalent viscous damping coefficient curves

采用积分方法计算各试件的累计耗散能量曲线如图12所示。图12可以看出：当位移达到40 mm时，D8–S55耗散能量最大（14.99 kJ），其次为D6–S86耗散能量（12.56 kJ），D6–S60和D6–S50耗散能量接近（约为8.5 kJ），D4–S60和D4–S50耗散能量最小（不高于4 kJ）。D8–S55对比D4系列，耗能从3.62增加至14.99 kJ，提高了314.09%。由此可见，D8–S55耗能能力最优。

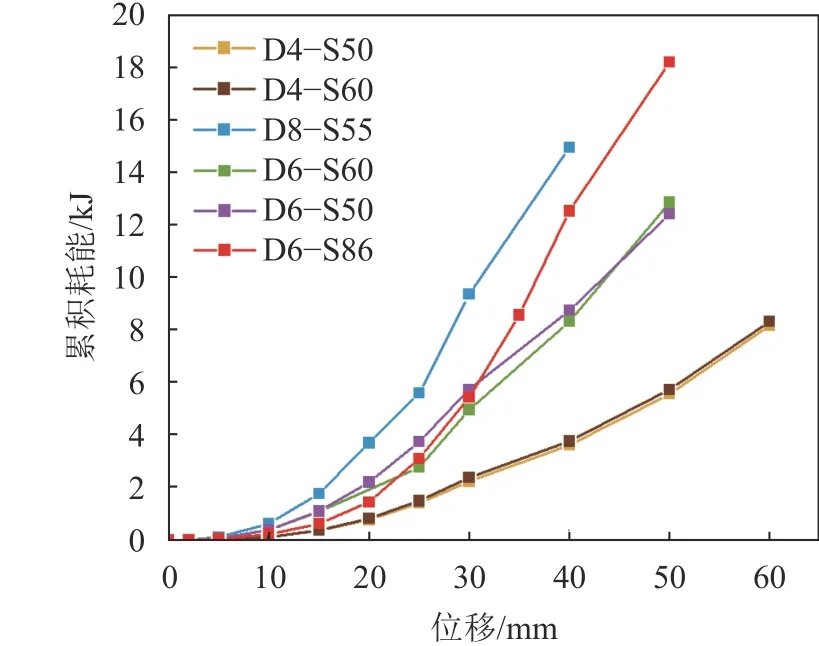
图12 累积耗能曲线Fig. 12 Cumulative energy consumption curves

4 耗能节点力学指标计算

4.1 钢板–CLT连接端抗剪承载力

目前，国内还没有相应的规范标准计算正交胶合木–钢板连接端抗剪能力。本文参照Eurocode 5计算钢板–木连接节点抗剪承载力，Fγ,RK为单个螺钉连接钢板与木构件的抗剪承载力，考虑3方面的最小值，计算公式为：

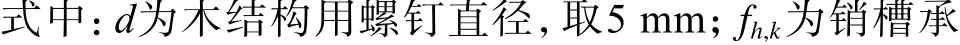
经式（1）计算得出单个螺钉连接的钢–木节点抗剪承载力为2 050.07 N，本文提出的耗能连接节点共有18根LBS5x70螺钉进行锚固，不考虑节点群整体折减效应，故正交胶合木锚固端钢板螺钉连接的抗剪承载力为36.90 kN。

由于试件D8–S86极限承载力达到近30 kN，接近估算得出的木节点锚固端抗剪承载力36.90 kN，故可判断该连接节点由锚固端与环形阻尼器共同承担抗剪承载力，因此试验结果为滞回环呈“捏拢”形态。其余试件最大承载力（均在20 kN以内）均远小于木节点抗剪承载力。

4.2 环形耗能钢板的力学指标U型阻力器

设t为U型阻力器耗能段钢板厚度，b为宽度，R为圆弧处半径， σy为阻尼器钢材的屈服强度，E为钢材的弹性模量。

假定U型阻尼器上下耗能段同时各有一个截面进入全截面塑性屈服，如图13所示。将式（2）代入式（3）可得式（4），可求得屈服荷载Fy。

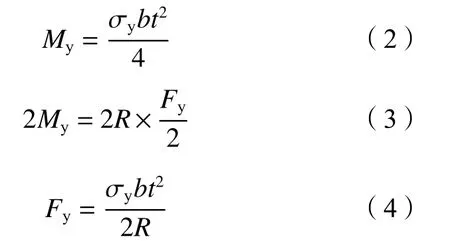
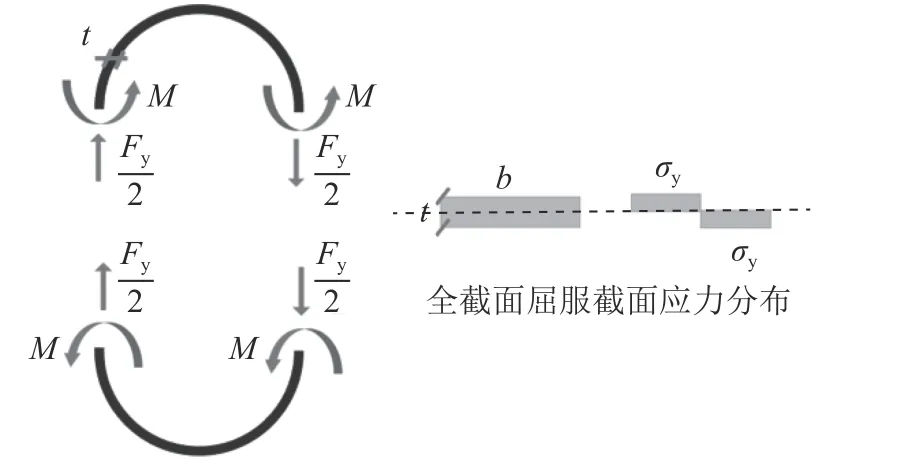
图13 阻尼器计算简图Fig. 13 Damper calculation diagram

基于能量方法与绕圆弧段弯矩积分，得到屈服位移Uy计算公式（5），将式（4）代入式（5）整理得最终的Uy计算公式（6），由初始刚度K0=Fy/Uy得到K0的计算公式（7）。

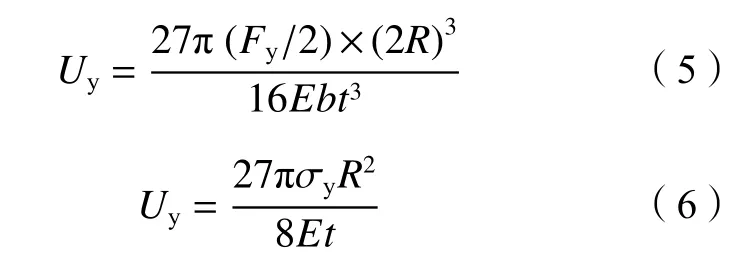
将Q235钢材的弹性模量E=210 GPa、σy=285 GPa及各试件的尺寸数值代入到理论公式（4）、（6）和（7）中，可分别计算出环形耗能节点的屈服荷载Fy、等效屈服位移Uy、 初始刚度K0。与计算值进行对比，见表5。

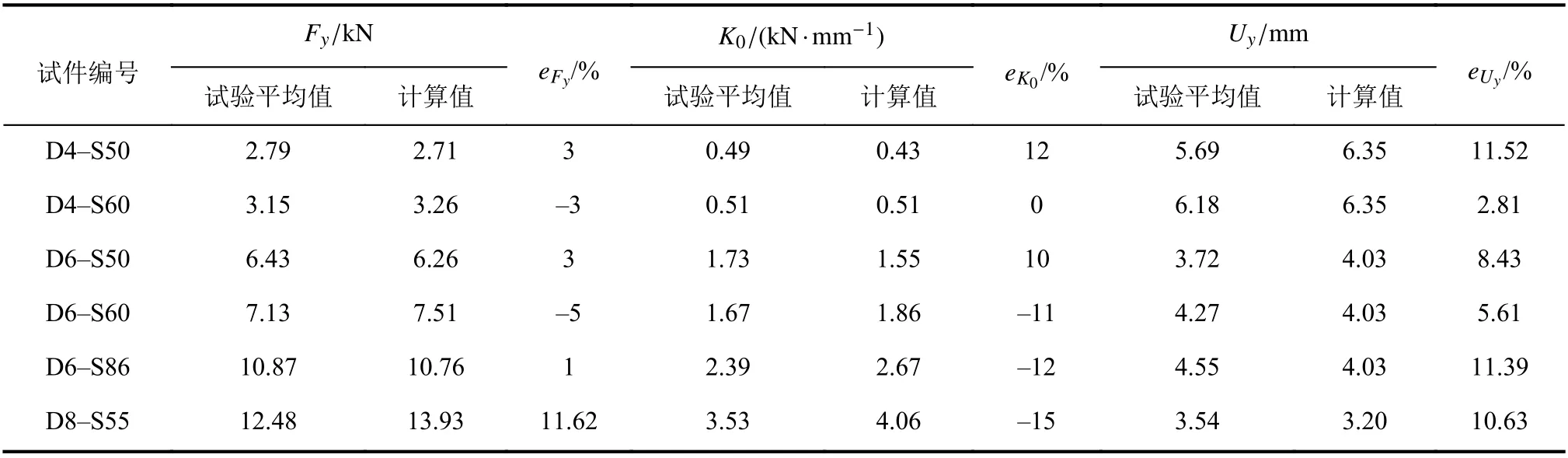
表5 阻尼器力学指标试验值与计算值对比Tab. 5 Comparison of experimental and calculated values of mechanical indexes of dampers

从表5可以看出，计算值与试验值相比较，所有试件3项力学指标误差值均在15%以内，并且计算值与试验值趋势保持一致。结果表明，该理论计算合理可行，相比于标准角钢连接件连接的节点，本文提出的耗能节点的承载力可以进行准确评估与可控设计。

5 环形耗能阻尼器的有限元分析

采用有限元软件ABAQUS随动硬化模型[31]和C3D8R单元建立实体模型，模拟耗能节点的试验结果。因为试验正交胶合木锚固端与钢梁的锚固端均为强连接，故简化锚固端为刚接，对双U型弯板进行数值模拟。由于篇幅所限，图14仅展示D4–S60和D6–S50的数值模拟与试验的滞回曲线对比，图15为其余耗能节点试验与数值骨架曲线对比。由图14、15可知有限元模型可以较为准确地模拟耗能节点的力学行为，从而实现合理的节点设计和准确的承载力预测。结合进一步的数值模拟分析研究可知，此类节点设计原则与性能期望是在保证锚固端为强连接的前提下，环形阻尼器集中耗能，设计的环形阻尼器抗侧刚度越高、承载力越高，其耗能能力越强，该节点设计越理想。环形阻尼器承载机理是通过平直段的弯曲进行耗能，为弯曲型阻尼器，故节点设计可以通过改变板厚、宽度及圆弧段半径等参数设计出不同屈服荷载及位移水平。

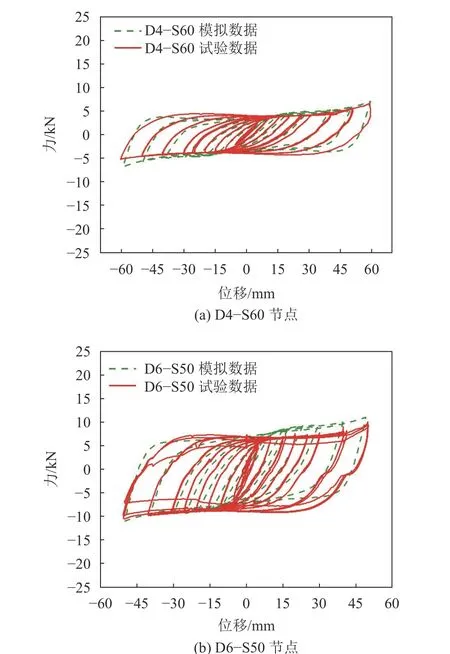
图14 试验与模拟滞回曲线对比Fig. 14 Comparison of experimental hysteresis curves and simulated hysteresis curves

图15 试验与模拟骨架曲线对比Fig. 15 Comparison of experimental skeleton curves and simulated skeleton curves

6 结 论

本文提出了一种由U型阻尼器组成的环形耗能节点，连接正交胶合木墙体与基础钢梁，设计并制作了7个不同尺寸的连接节点，通过开展低周往复抗剪试验，研究其滞回特征、承载力退化、刚度退化与耗能规律等，探讨了收腰及厚度对节点力学性能的影响，给出了正交胶合木锚固端抗剪承载力公式、由双U型拼接的环形Q235阻尼器力学指标计算公式及进行有限元数值模拟，三者结合为正交胶合木耗能连接设计提供依据。

1）除节点D8–S86以外，其他节点滞回环饱满稳定，保证与正交胶合木墙体锚固端为强连接，将对墙体的损伤集中到耗能试件上，在保护正交胶合木剪力墙同时可以实现承载力及破坏模式可控，且连接损坏后可更换、修复。

2）结合《木结构设计标准》、Eurocode 5及《木结构用自攻螺钉》等标准，对螺钉连接的钢板–正交胶合木钉连接的锚固端抗剪承载力进行初步估算，为耗能节点承载力设计提供依据。

3）耗能节点的平直段起主要的耗能作用，平直段收腰程度越大，滞回环越稳定饱满。通过推导力学指标公式可知：阻尼器腰部宽度与初始抗侧刚度及抗侧屈服力成正比；钢板厚度对初始抗剪刚度及抗剪屈服力影响明显，厚度的立方与初始抗剪刚度呈正比，厚度的平方与抗剪屈服力成正比。该环形阻尼器节点的主要力学性能指标计算公式，可以较为准确地预测节点的屈服承载力、初始刚度与屈服位移。

4）通过有限元软件ABAQUS建立耗能节点有限元模型，较为准确地模拟耗能节点的抗剪行为。

5）在保证锚固端为强连接的前提下，环形阻尼器集中耗能，设计的环形阻尼器抗侧刚度及承载力越高，其耗能能力越强，该节点设计越理想。结合试验现象与试验结果可知，保证锚固端不破坏前提下，试件D8–S55抗剪抗侧刚度及承载力最高，且耗能能力最佳，未来可用于正交胶合木结构的耗能节点连接。