基于分散式储能的风电柔直并网直流故障穿越协调控制
孙银锋,刘宇晗*,郭宇航,李国庆,王振浩,吴学光
(1.现代电力系统仿真控制与绿色能源新技术教育部重点实验室(东北电力大学),吉林 吉林 132012;2.全球能源互联网研究院,北京 102211;3.直流电网技术与仿真北京市重点实验室,北京 102211)
为构建清洁能源供应体系,高比例新能源的输送与消纳能力亟需提升,加大电能替代力度成为首要任务[1–2]。基于模块化多电平换流器的多端柔性直流输电系统(multi-terminal HVDC based on MMC,MMC–MTDC)已经证明了其在风电并网与消纳[3]、孤岛供电[4]、提升电网稳定性[5]等方面的优势,现已成为直流输电系统的首选方案[6],在海上风电并网与多电网互联等领域拥有广阔的前景[7]。
随着电力系统电压等级和传输距离的提高,直流线路架空线具有显著的经济优势,但同时增加了故障发生率。在柔直输电系统中,直流故障发展更为迅速,对电网冲击更大。因此,提升系统直流故障穿越能力成为目前研究的重点。现有针对柔性直流输电系统直流故障穿越措施的研究主要分为以下2个方面:一是,改进换流器或子模块拓扑,使其具备故障自清除能力。曹帅等[8–9]采用半桥与全桥子模块组成的混合型MMC,可以在故障期间不闭锁持续运行,具有良好的故障阻断能力。王冰冰等[10]提出一种储能内置式子模块拓扑结构,可以实现故障自我隔离与故障后快速恢复。但新型子模块更复杂的控制方式与更高的成本使得此方法在实际工程应用中受限。二是,采用半桥子模块与直流断路器(direct current circuit breaker,DCCB)相互配合迅速隔离故障线路[11–12]。该方案在舟山柔性直流电网与张北500 kV直流电网中已得到实际工程应用[13–14]。
针对直流线路双极接线方式,在直流线路单极故障期间,可以通过非故障极继续传输功率,由于非故障极无法承担全部的功率输送,较大的剩余功率会涌入非故障极造成换流站过载[15]。目前工程上针对剩余功率消纳问题采用耗能方案进行消耗,主要分为以下2种方案:一是,通过在风电场交流侧汇流母线处并联耗能电阻,以维持故障期间系统的稳定性[8–9]。二是,在换流站直流侧配置耗能装置[16–17]。耗能装置中全控型电力电子器件较多,拓扑复杂且经济成本高昂[18]。控制逻辑设计困难、能源浪费与散热设施建设等问题也在制约该方法的进一步发展。
工程中普遍使用的耗能电阻阻值相对固定,只能成组投退,对电网运行冲击性较大。当系统运行方式不同时,无法针对不同运行状态与故障类型准确消纳不平衡功率。因此,相较于采用耗能方式进行故障期间的功率消耗,采用风力发电机配置的储能系统进行故障穿越更具研究价值。储能系统吸收剩余功率方案复杂程度更低,可以实时监测系统运行状态,当故障发生时根据不同故障类型定量计算不平衡功率,使功率消纳更为准确。郑子萱等[19]提出了一种依托于储能装置的交流故障穿越新方法,通过多种方案的对比证明了在储能装置介入的情况下可以更有效的维持直流电压稳定。但单独采用储能系统消纳功率的方法需要为储能系统配置过高的容量,投资成本过高,很难应用于实际。杨航等[20]在风电机组全功率换流器直流链路设置储能系统,通过DC/DC变换器对储能系统的控制提高了风电机组的故障穿越能力和故障期间运行稳定性,但仅关注交流故障抑制方面,未涉及故障发生率更高的直流故障。Jannati等[21]提出在风电场汇流母线处并联储能系统,通过输出功率跟踪和效用约束降低储能系统容量与损耗,延长储能单元寿命,变相提高了储能系统的经济性。但研究重点侧重储能系统对电网故障期间的能量吸收与故障后的快速恢复,未能将定量分析与新能源出力相互配合,降低了系统的整体故障穿越能力。
为解决上述问题,本文建立了风电接入多端柔直输电系统和储能系统的拓扑结构和数学模型;通过多端柔直系统的直流故障特性分析,根据非故障极换流站的功率传输能力,确定了自消纳与非自消纳情形;根据断路器重合闸信息判断的不同故障类型和功率消纳情形调整换流站控制方式,设计分散于风力发电机组全功率换流器预装的储能设备参数,吸收故障期间的不平衡功率,进而提出完整的故障穿越协调控制策略,有效减小故障的影响范围,保证风电机组出力和系统的稳定运行。最后通过数字仿真验证了本文所提控制策略的有效性。
1 风电经对称双极MMC–MTDC并网的系统结构、运行方式及控制策略
1.1 MMC–MTDC系统结构与运行方式
风电经对称双极MMC–MTDC系统并网结构如图1所示。
由图1可知,直流电网为对称双极接线,正负极输电线路分别形成环网,每一端由正负极两个换流站构成,直流输电线路始末两端均配备直流断路器。永磁直驱风力发电机通过全功率变流器与电网连接,并采用等值模拟原理构建风电场。储能系统并联在风力发电机全功率变流器的直流线路上,主要包含DC/DC变换器及储能单元两部分。
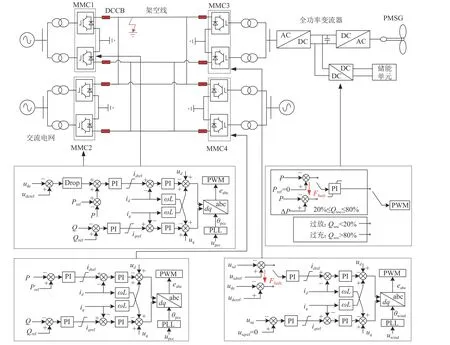
图1 风电场经MMC–MTDC并网系统拓扑及控制框图Fig. 1 Topology and control block diagram of grid connected system of wind farm via MMC–MTDC
相较于两端输电系统,多端网络需要配置站间协调控制策略,用以调整直流线路电压、各换流站传输功率等指标,维持直流电网稳定。下垂控制由于具有功率调节快、直流电压稳定性好等优点,已广泛应用于直流系统的直流电压控制,相较于单一主站控制还可以避免因主换流站容量不足而限制系统的功率波动调节能力。换流站MMC1与MMC2采用直流电压下垂控制,共同承担故障期间系统中的电压波动。对MMC3和MMC4分别采用孤岛控制与定有功功率控制,维持系统功率平衡。
采用对称双极接线方式的MMC-MTDC系统具有可靠、灵活的运行特性,发生故障时可以改变系拓扑结构,通过非故障极保证故障期间风功率的及时送出与消纳[22]。稳态运行时,系统通过正负极传输功率,当其中一极发生故障时,快速切除故障极线路防止故障电流危害系统稳定性,此时故障极停止传输功率,仅由非故障极线路保证故障期间的功率传输。
1.2 MMC结构与数学模型
三相MMC换流器拓扑结构及原理如图2所示。由图2可知,换流器由三相上下桥臂组成,各桥臂含有数量相同的子模块(sub module,SM)并与桥臂电感串联,交流侧从上下桥臂相连处接入。MMC直流侧输出电压由每一相上下桥臂子模块电容支撑,见式(1):
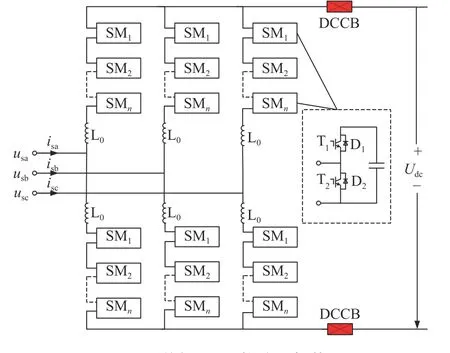
图2 单极MMC换流器拓扑Fig. 2 Topology of unipolar MMC converter

式中,uip与uin分别为每相上、下桥臂子模块电容电压之和,Udc为直流线路电压。为保持稳态运行时直流母线电压不变,则需保证每相上下桥臂投入子模块数量满足:
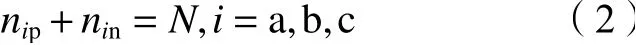
式中,nip与nin分别为每相上、下桥臂子模块投入数量,N为每相桥臂串联子模块个数的一半(不考虑冗余)。
MMC采用矢量控制方式,基本控制策略可分为功率外环控制与电流内环控制。功率外环主要是对有功功率、无功功率、直流电压、交流电压等物理量进行控制,并输出dq轴的电流参考值至电流内环控制器,内环控制实现对参考值的快速跟踪。
建立dq旋转坐标系下MMCm的时域输入输出基频表达式[23]:

式中,Lm和Rm分别为MMCm的等效电阻和等效电感,ω为各换流站交流电网角频率,usdm和usqm分别为MMCm上、下桥臂差模电压的d轴和q轴分量,udm、uqm、idm、iqm分别为MMCm交流侧输入的电压与电流的d轴和q轴分量。
通过Laplace变换将式(3)从时域变换到频域,可得:
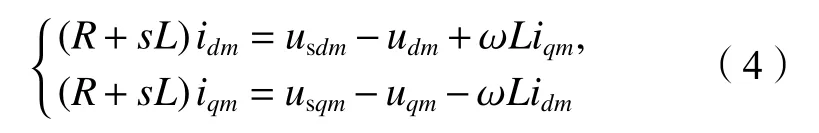
根据三相瞬时功率理论,dq坐标系下MMCm与交流系统交换的瞬时有功功率和无功功率可表示为:

在三相电压平衡条件下,取三相电压合成矢量方向为d轴方向,则usdm=Us(交流系统电压幅值),usqm=0。与由式(5)可知,有功功率仅与idm有关,无功功率仅与iqm有关。根据上述原理可设计换流站的内外环控制器结构。
1.3 储能系统参数设计
如图1所示,储能系统并联在全功率变流器直流线路上,区别于储能系统集中式接入交流系统,分布式接入的储能系统容量小、成本低,并省略双向DC/AC换流器,减少不必要的电力电子器件。DC/DC变换器根据故障信号切换运行模式,控制储能系统吸收或发出有功。系统稳定运行时,储能系统退出运行,与电网不发生能量交换;故障发生时,直流断路器迅速动作并产生故障信号,DC/DC变换器切换到充电模式,储能单元吸收有功,消纳故障期间电网中的不平衡功率。由于风力发电机预装的储能装置有着平滑功率输出等作用,因此在满足系统稳定性要求与不影响其他功能的前提下,合理配置储能系统相关参数,尽可能减小储能系统额定容量,在安全性与经济性两方面对于多端直流输电系统具有重要意义。
储能系统配置的额定有功功率与风电场额定输出功率和换流站单极最大输送功率有关,三者满足的不平等约束条件为:

式中,Pbess为储能系统的额定有功功率值,Pmmcmax为单极换流站最大输送有功功率值,Pwindmax为风电场输出的额定有功功率值,极限情况下式(6)等号成立。同时,考虑功率冗余与直流电网正负极对称性,换流站正常工作传输的功率小于最大输送功率,单极换流站最大传输有功功率值的2倍不小于风电场输出的额定有功功率,见式(7):
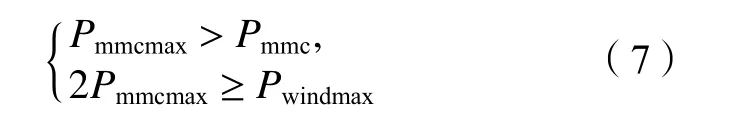
式中,Pmmc为单极换流站正常工作时传输的有功功率。
综合考虑系统功率平衡原理与经济性因素,当系统发生单极故障时,非故障极换流站与储能系统承担功率之和与风电场输送功率之间的差值决定了系统的功率冗余,风电场输送功率的最大值为额定有功功率。
从初始充电状态开始,对流经电池电流积分,确定电池的荷电状态与剩余容量。对荷电状态上下限进行约束,防止储能系统过量充放电造成元件损坏[24–25]。荷电状态Qsoc公式与约束条件为:
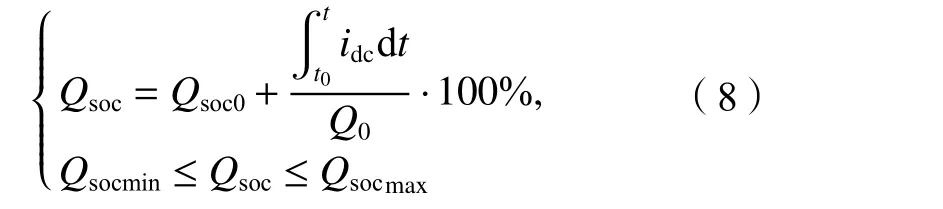
式中:Q0为电池的额定容量;Qsoc0为电池的初始充电状态,可通过将开路电压与电池制造商提供的特性进行比较来获得。设置Qsocmin=20%,Qsocmax=80%。
为保证系统发生单极故障时储能系统与换流站均不发生过载,考虑故障期间非故障极换流站功率传输能力会明显减小储能系统容量。根据分布式储能装置特性,储能设备的容量为:
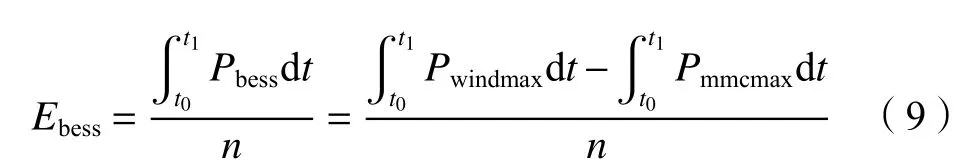
式中,n为构成风电场的风机总台数,Ebess为每台风力发电机预装的储能系统用于故障穿越功能的额定容量,t0和t1分别为直流断路器两次动作的时间。
2 直流故障特性分析及故障穿越协调控制策略
2.1 直流故障特性分析
图3为子模块放电回路。由图3可知,当风电经对称双极MMC–MTDC并网系统直流输电线路发生单极短路接地故障时,故障点对地电压瞬间跌落至0,故障极换流站中的子模块向故障点迅速放电产生过电流,严重危害电网安全。
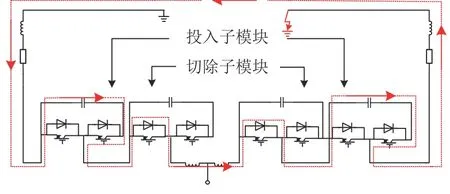
图3 MMC子模块放电回路Fig. 3 Discharge circuit of MMC sub module
由于换流站所采用的半桥型子模块无法自动清除故障,子模块电容不断放电导致自身电压不断降低,无法维持风电并网点电压稳定,导致风电场交流侧汇流母线电压迅速降低,等同于风电场并网点发生三相故障,对风电场安全运行产生极大冲击。为快速隔离故障线路,抑制故障电流,采用直流断路器对故障极线路快速切除。由于故障极换流站桥臂电感的存在,故障线路被隔离后换流站内部电流无法瞬间降至0,交流侧电流会通过某相桥臂的反并联二极管向其他各相所连桥臂中的子模块持续充电,造成故障极子模块的过电压。此时如果将故障极换流站切除,当故障结束后换流站的重启会对电网造成较大冲击,此种措施在实际工程中未得到大规模应用。因此,在故障持续期间,改变故障极换流站控制方式为定直流电压控制,既可以抑制因交流馈入导致的子模块电容过度充电,又可以实现不闭锁持续运行。
2.2 故障情景与穿越措施分类
2.2.1 单极故障
在实际工程领域,已实现直流断路器在故障发生6 ms内快速隔离故障,有效抑制故障电流的快速上升。通过辅以切换换流站控制方式可以有效控制电压稳定,保证风电机组不脱网持续运行。直流线路发生单极故障时,尽可能保证风电场输送到直流电网的功率保持不变,精准消纳故障期间系统产生的不平衡功率成为首要任务。
此时系统中产生的不平衡功率ΔP与正常工作时换流站功率相等,即ΔP=Pmmc,单极故障期间非故障极换流站可吸收的功率为:
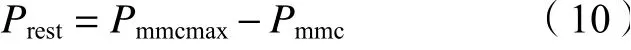
式中,Prest为非故障极的裕量功率。根据Prest与ΔP的大小可分为2种功率消纳方案,图4为两种方案下故障期间功率流通路径。具体的功率消纳方案如下:
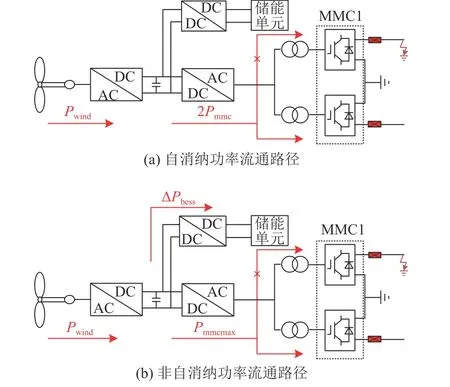
图4 故障期间功率流通路径Fig. 4 Power flow path during fault
方案1:非故障极换流站不平衡功率自消纳,此时要求 ∆P≤Prest,系统产生的不平衡功率可以完全由非故障极消纳。在此情形下系统发生故障,不需要风电场与储能系统参与系统功率调节,风电场与受端网络在故障结束后可快速恢复至稳态,一定程度上减小故障影响范围,提升系统稳定性,功率消纳路径如图4(a)所示。
方案2:非故障极换流站无法完全消纳不平衡功率,此时ΔP>Prest,优先控制非故障极换流站达到满载运行状态,系统产生的不平衡功率在非故障极满载后仍有剩余,这一部分的剩余功率由储能系统承担。此时储能系统参与功率流通如图4(b)所示,将不平衡功率分配到每台风机配备的储能单元上,每台风机的储能装置吸收的功率为:
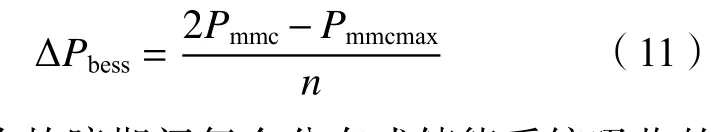
式中,ΔPbess为故障期间每个分布式储能系统吸收的功率。
单极故障发生时,直流断路器在6 ms内完成对故障线路的隔离,考虑最严重的情况为非故障极换流站满载,储能系统参与吸收不平衡功率。储能系统容量与直流断路器重合闸时间存在约束关系,要求直流断路器两次动作时间差内,储能系统额定功率运行不会超出容量限制。当重合闸失败时,发出永久故障信号,储能系统与风电场接收信号,储能系统退出运行不再吸收能量,风电场减载的功率与故障期间储能系统吸收的功率关系为:

式中,ΔPwind为风电场减载功率。此时风电场输出的功率为Pwind–ΔPwind,正常工作条件下系统正负极换流站完全承担风电场输出功率,即Pwind=2Pmmc,将式(12)代入,可得风电场减载后输出功率为Pmmcmax。功率分配改变后系统达到永久故障下新的稳定状态。
对于架空输电线路,直流侧单极故障的发生是最为频繁的,故障类型分为瞬时故障与永久故障两种情况。本研究以直流断路器重合闸情况判断故障类型:若直流断路器成功重合闸,则为瞬时故障,否则为永久故障。考虑功率消纳方案与不同的故障类型,共计4种情形。本文提出的完整故障穿越流程如图5所示。由图5可知:自消纳前提下的瞬时故障。此时风功率可完全由非故障极传输,发生瞬时故障后,储能系统与风电场不动作,非故障极换流站增大传输功率至故障前的2倍。故障结束后将直流网络每一端的故障极换流站从定直流电压控制切换回稳态控制模式,不再参与额外的功率消纳。非自消纳功率情况下发生瞬时故障,故障期间由非故障极换流站和储能系统共同承担不平衡功率,待直流断路器重合闸后储能系统退出运行,控制非故障极换流站减小功率承担至与故障极换流站相等,完成故障穿越。自消纳前提下的永久故障不需要储能系统与风电场参与功率转移,可完全由非故障极换流站承担,功率分配方案与瞬时故障相同。
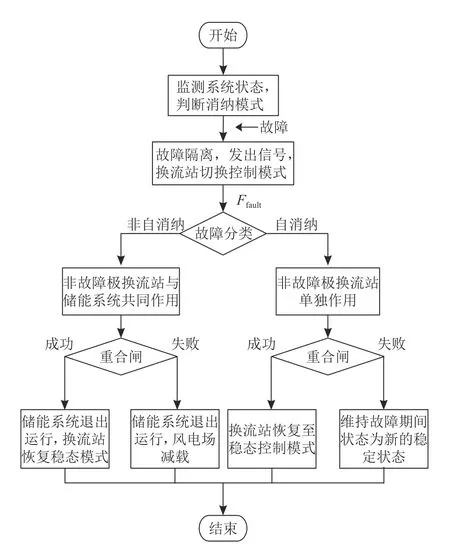
图5 系统故障穿越协调控制流程Fig. 5 System fault ride-through coordination control process
图6为系统在非自消纳前提下发生永久性故障的功率流通示意图。直流断路器第1、2次动作期间功率流通与瞬时故障相同。由图6可知,重合闸后储能系统停止吸收功率,风电场输出功率减小并仅由非故障极换流站传输。
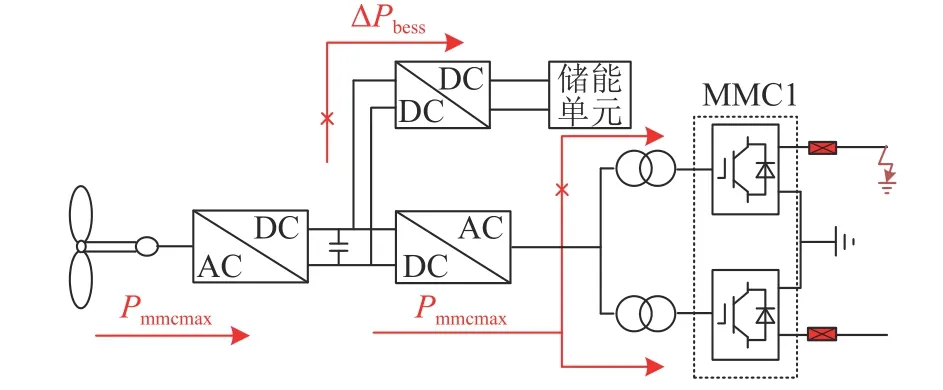
图6 非自消纳前提下永久故障功率流通情况Fig. 6 Permanent fault power flow under the premise of non-self absorption
2.2.2 双极故障
系统发生双极短路故障时,由于双极短路时无法通过换流站消纳部分功率,式(9)与(11)中Pmmcmax为0,可得储能系统满足双极故障穿越条件的容量应大于单极故障时容量,因此设置储能系统容量应以双极故障情形为准。
双极故障穿越流程:当直流线路发生双极短路时,直流断路器动作将正负极线路隔离,直流线路无法传输功率。正负极换流站均需改变控制模式至定直流电压控制以防止交流侧电流馈入子模块电容造成过载。储能系统接收断路器跳开信号进行功率消纳至断路器第2次动作时刻。若为瞬时故障,重合闸成功后系统恢复至故障前状态;若为永久性故障,则风电场减载,减载功率根据式(12)计算。从故障穿越措施角度而言,双极故障本质上为不含非故障极换流站配合的协调控制措施,属于单极故障穿越措施的一部分,因此本文并未对于双极故障进行单独仿真研究。
3 仿真分析
为验证本文提出的故障穿越方案的有效性,在PSCAD/EMTDC仿真平台搭建如图1所示的风电经对称双极MMC–MTDC并网系统的仿真模型,通过稳态仿真验证模型合理性后,对自消纳与非自消纳前提下的单极短路故障穿越措施进行仿真验证。
模型中采用等值模拟方法构建额定有功功率为1 000 MW风电场,由210台额定功率为5 MW的风机组成,交流汇流母线电压为380 kV。风电机组出口电压为0.69 kV,经全功率变流器与汇流母线相连,汇流后并入MMC3。设置直流断路器两次动作时间间隔为0.3 s,进行双极故障条件下的储能系统容量配置计算,根据式(9)与(11)计算可得式(13):
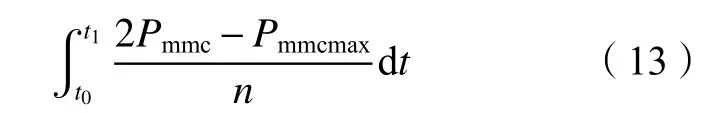
预装储能单元用于故障穿越的容量约为0.41 kWh。考虑储能系统的平滑风机出力及风电场黑启动等作用[26],容量以需要的最大值为准为1 kWh[27–28]。其他仿真参数见表1,功率流动以流向直流电网为正方向。
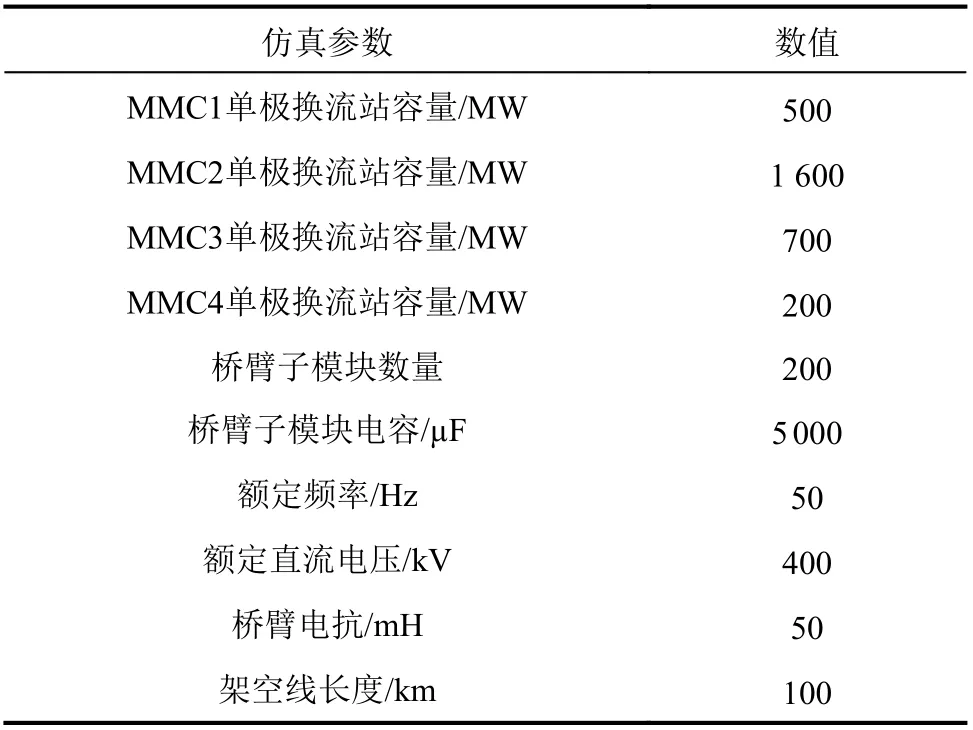
表1 系统仿真相关参数Tab. 1 System simulation related parameters
3.1 稳态运行验证
为验证搭建仿真模型的合理性,系统在稳态情况下运行时仿真如下。
图7为直流线路正负极电压。由图7可知:系统启动后,MMC1的正负极换流站在0.2 s时解锁并投入运行,建立直流电压,并维持电压稳定在400 kV,为其他换流站投入运行创造电压稳定条件。MMC2与MMC4分别在0.4和0.6 s解锁,与风电场相连的MMC3在0.8 s时解锁,为风电场端提供交流侧稳定电压。风电场与全功率变流器在0.8 s时接入,直流线路电压因建立全功率变流器直流电压而产生波动,待风电场端完全启动后,系统直流线路电压恢复稳定。
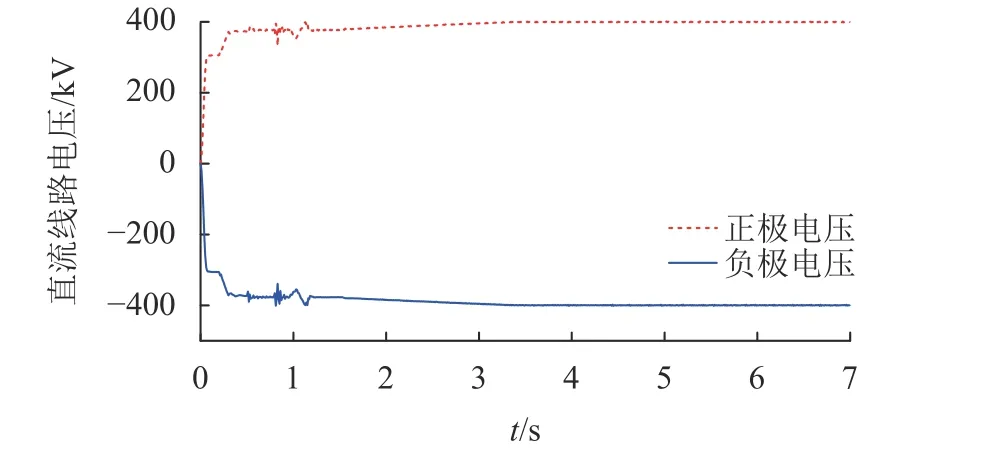
图7 直流线路电压Fig. 7 DC line voltage
图8为风电场交流侧汇流母线电压与注入系统的有功功率和无功功率仿真结果图。由图8可知,在t=0.8 s前,风电场处于闭锁状态,未向系统注入功率,汇流母线电压与传输功率均为0,风电场自0.8 s接入系统,汇流母线处交流电压在t=1.2 s达到稳定状态。此后风电场输出的有功功率不断增大,在t=3.3 s达到最大值约为1 000 MW,
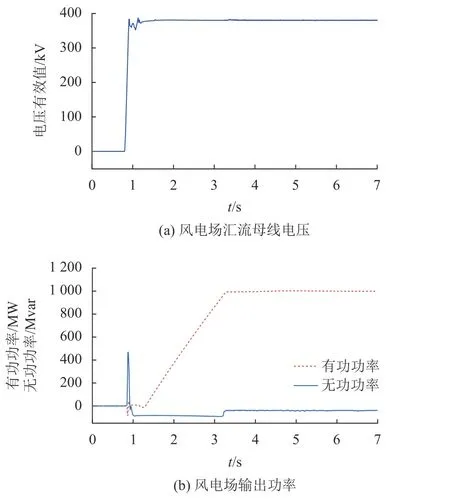
图8 稳态下风电场汇流母线电压及输出功率Fig. 8 Wind farm bus voltage and output power in steady state
稳态仿真中,有功功率传输情况如图9所示。由图9可知:风电场在3.3 s后达到额定输出功率,风电输出不再增加,各换流站功率传输趋于稳定。稳态期间储能系统不参与功率流通。上述仿真结果可以表明,所搭建的仿真模型在系统稳定后可以较好地反映系统状态,为后续提出故障穿越措施提供验证平台。
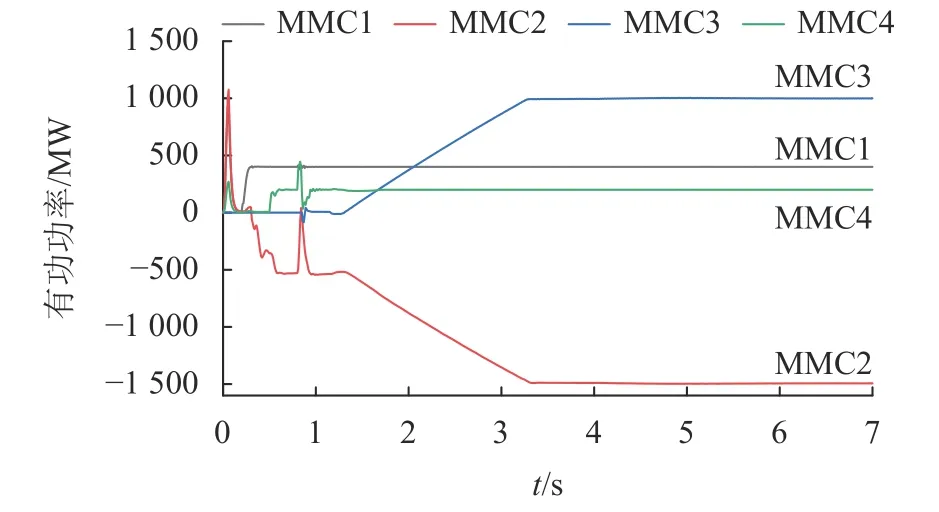
图9 稳态下各换流站有功功率Fig. 9 Active power of each converter station in steady state
3.2 非自消纳情形下直流故障
3.2.1 非自消纳情形下瞬时故障
为验证非自消纳情形下瞬时故障的故障穿越措施,在t=5 s时于MMC1出口处设置正极直流母线瞬时故障,持续0.2 s后结束。直流断路器在故障发生2 ms后发出故障信号,在6 ms后隔离故障线路。
系统接收直流断路器动作信号后转变为故障穿越模式:在非自消纳前提下,非故障极换流站无法完全传输风电场输出功率,根据非故障极换流站与储能系统容量,由式(11)计算功率分配方案。系统接收直流断路器动作信号后转变为故障穿越模式:有功功率停止进入故障极换流站,改变故障极换流站控制方式为定直流电压控制,防止交流侧电流馈入对换流站子模块进行过充电。令非故障极换流站满载,有功功率由稳态的500 MW上升至700 MW。储能系统接收故障信号转变为充电模式,从直流线路吸收能量,承担的有功功率之和为300 MW。分配到每台风机的储能单元吸收的有功功率约为1.36 MW。
图10为单一储能单元功率传输情况。由图10可知,在非自消纳前提下,储能系统于5.002 s接收故障信号,开始向电池充电,此时产生持续时间约20 ms的较大波动。故障持续期间稳定从全功率变流器的直流线路吸收约1.36 MW,防止风机产生的不平衡功率过量涌入非故障极换流站造成换流站过载。
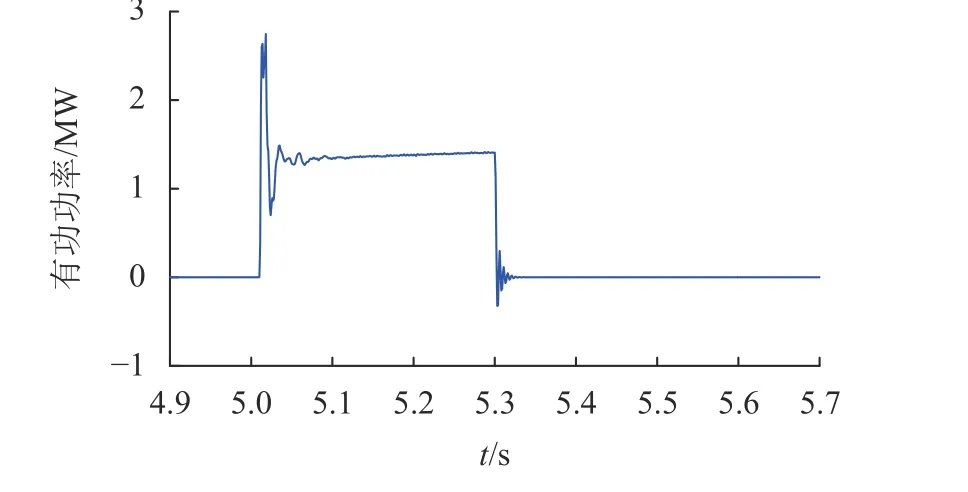
图10 储能系统吸收有功Fig. 10 Active power absorbed by the energy storage system
图11为风电场输出功率与汇流母线电压电流波形。由图11(a)可知,风电场对外输送功率由稳态的1 000 MW经储能系统吸收后,故障期间稳定在700 MW,符合单极换流站最大容量要求。图11(b)表明风电场交流侧汇流母线三相电压在故障持续期间未发生较大波动,可以保证风机的不脱网持续运行。由图11(c)可以看出,由于部分有功功率被储能系统吸收,风电场对系统注入功率的下降导致汇流母线三相电流在故障期间维持在较低水平且保持相对稳定状态。故障结束后,电流快速恢复至正常水平。
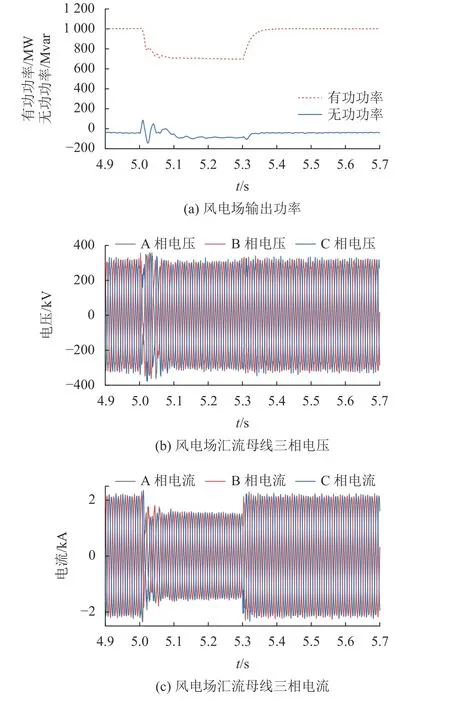
图11 风电场输出功率及汇流母线电压电流Fig. 11 Wind farm output power and bus voltage and current
图12为故障期间各换流站功率流通情况。由图12可以得到:由于直流断路器在故障发生后隔离故障线路时间有所延迟,MMC1与故障点直接相连,直流线路电流瞬间增大,造成MMC1功率上升且流向故障点。与交流电网相连的MMC2缺少来自MMC1的功率输送,从直流线路吸收的功率值有所下降。随着故障线路的切除,MMC1功率恢复正常值。风电场向直流电网注入功率因储能系统吸收而小于稳态注入功率,MMC2从直流电网吸收的功率值在故障持续期间均维持在较低水平。在t=5.3 s时断路器重合闸成功,储能系统退出运行,各换流站有功恢复至稳态值。
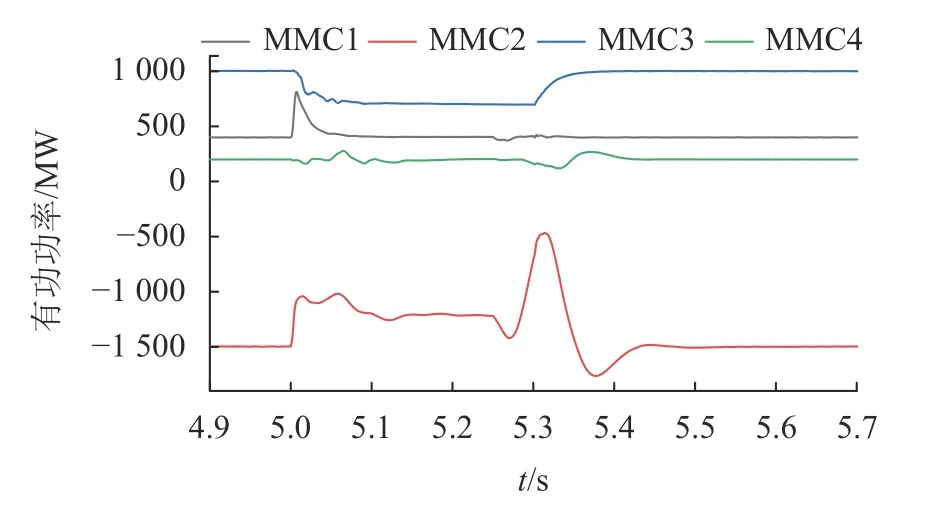
图12 换流站传输功率Fig. 12 Power transmitted by converter station
3.2.2 非自消纳情形下永久故障
在非自消纳前提下,为验证本文的故障穿越措施对永久故障有较好效果,在t=5 s时于MMC1换流站出口处设置正极线路永久故障。直流断路器于故障发生2 ms后动作并发出故障信号,系统进入故障穿越模式。在直流断路器二次动作信号发出前,故障穿越流程与瞬时故障情形相同。在t=5.302 s时直流断路器重合闸并发出永久故障信号,储能系统接收信号后退出运行防止过充电,风电场减载功率与故障期间储能系统吸收功率相等。
图13为风电场输出功率及汇流母线电压电流波形图。在永久故障条件下,储能系统投切方案与瞬时故障完全相同,投入期间的吸收功率相对稳定,功率流通大小与瞬时故障情形一致。如图13所示:在t=5.3 s时重合闸失败发出永久故障信号,储能系统自动切除,风电场减载功率与故障期间储能系统吸收功率相等,风电场输出功率产生波动后迅速消失。自故障发生后,风电场输出功率与非故障极换流站最大容量基本相等,汇流母线三相电压与三相电流相对稳定,为风电场持续运行提供良好条件。
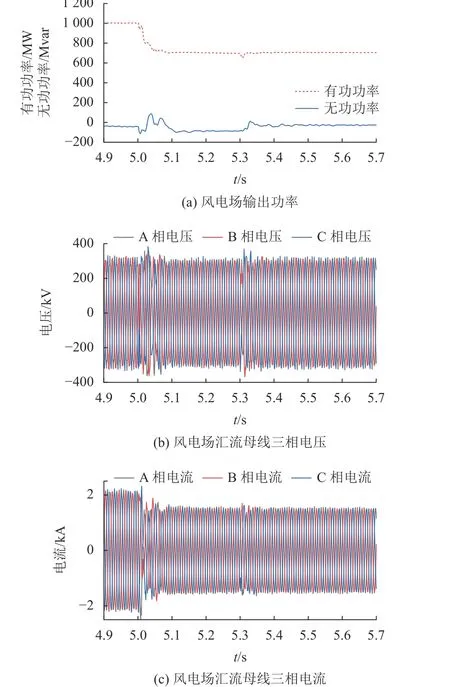
图13 风电场输出功率及汇流母线电压电流Fig. 13 Wind farm output power and bus voltage and current
图14为直流线路电压及负极传输的有功功率仿真结果。
图14(a)为换流站间正负极直流线路电压。由图14(a)可以看出:故障发生瞬间正极线路直流电压剧烈波动后变为零,负极线路直流电压由稳定状态的–400 kV变为故障后的–380 kV。在永久故障发生后,直流断路器隔离正极线路致使正极传输功率为0,负极线路承担全部的功率输送任务,负极线路电压的稳定关系到系统整体的稳定性。自故障发生后,经历直流断路器2次动作,最后到新的稳定状态,负极线路电压均未产生剧烈波动,可以通过负极线路稳定传输功率。图14(b)为各换流站间负极线路功率传输情况仿真结果,其中,Pij为MMCi与MMCj两换流站间传输的功率。由图14(b)可知:在直流断路器2次动作期间功率流通存在较大波动。在t=5.3 s时刻,直流断路器重合闸,因线路故障仍然存在,线路电压与负极功率产生剧烈变化。重合闸失败后直流断路器再次隔离线路,系统拓扑改变并达到新的稳定状态,功率分配方案为负极线路在t=5.3 s后稳定时刻所传输的功率。
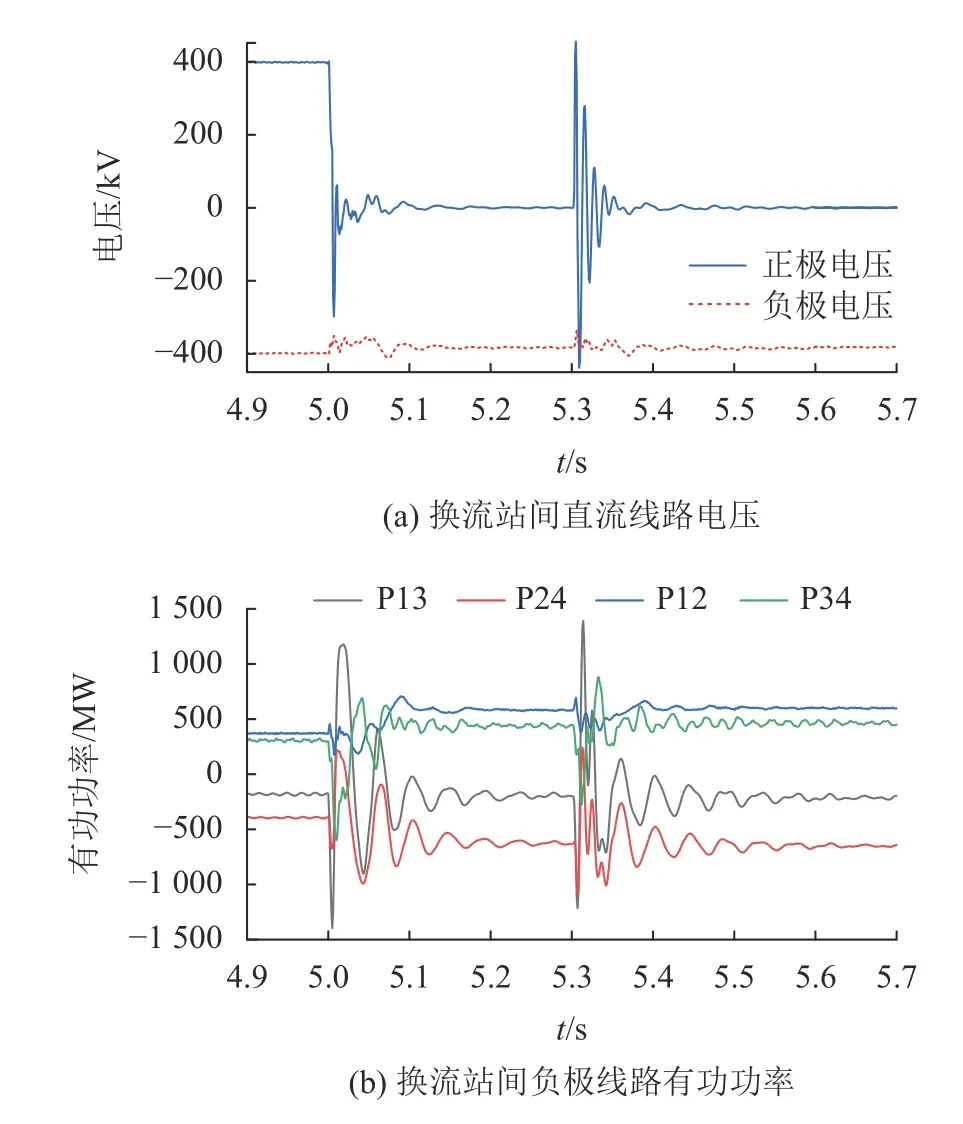
图14 直流电压及负极传输有功Fig. 14 DC voltage and active power transmitted by negative pole
3.3 自消纳情形下直流故障
3.3.1 自消纳情形下瞬时故障
为验证自消纳情景下故障穿越方案的可行性,设置相同条件下的瞬时故障。自消纳情形下风电场输出功率为500 MW,小于单极换流站的最大容量,故障期间储能系统不参与功率调节。
图15为风电场输出功率波形。由图15可知:风电场向直流网络输出的有功功率在故障前后保持稳定,无功功率在直流断路器动作时刻产生较小波动后快速消失。风电场交流侧汇流母线三相电压与三相电流在故障持续期间相比于稳态产生少许偏差,在故障结束后恢复至稳态水平。因此,自消纳情形下风电场未受到故障影响,本文提出的故障穿越措施有效减小了故障影响范围,显著提升系统整体稳定性。

图15 风电场输出功率Fig. 15 Wind farm output power
换流站传输功率及直流电压波形图见图16。
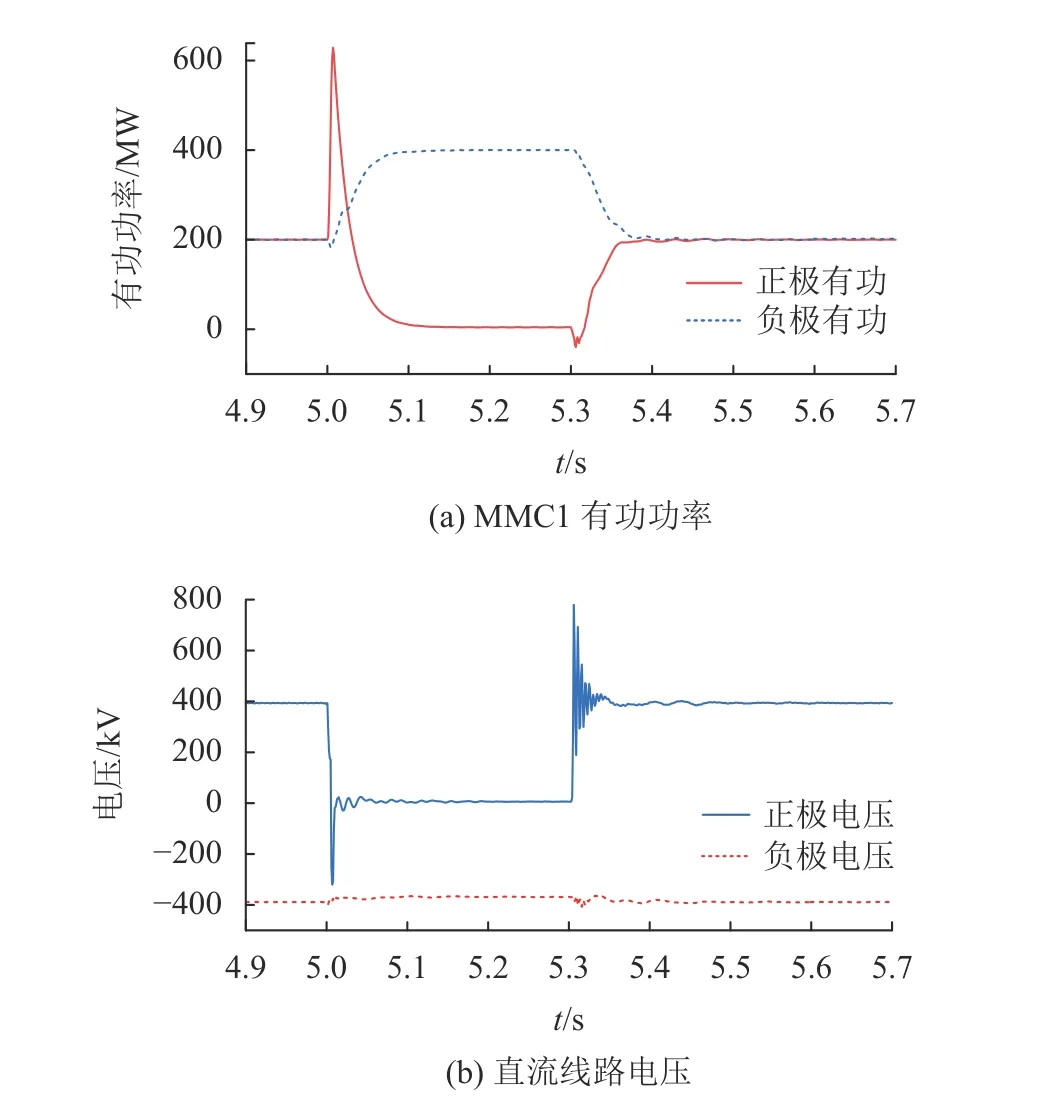
图16 换流站传输功率及直流电压Fig. 16 Transmission power and DC voltage of converter station
从图16(a)可以看出:换流站有功功率变化在故障前后未发生失稳情况。由于直流网络低惯性特点,与故障点直接相连的换流站MMC1的有功功率在故障发生时刻流向故障点,导致正极功率瞬间增大,故障恢复阶段正负极功率平稳回归稳态值。由图16(b)可知:负极线路电压在故障发生时刻与恢复时刻受到扰动产生变化,总体电压情况在故障穿越前后保持稳定。正极直流电压在故障持续期间为0,故障结束0.5 s内恢复至400 kV。直流线路电压在故障前后的相对稳定为直流电网故障穿越功率分配方案提供先决条件。
3.3.2 自消纳情形下永久故障
在t=5 s时设置MMC1出口处正极直流线路永久性故障,自消纳情形下无需使用储能系统平衡功率,故障期间非故障极换流站承担全部功率传输,不产生不平衡功率。直流断路器在第1次动作后间隔300 ms进行第2次动作,在t=5.302 s时重合闸,由于直流线路故障未清除,在t=5.304 s重合闸失败后发出永久故障信号,风电场接收信号不减载,输出功率保持恒定。风电场控制措施与瞬时故障一致,因此未绘制相关曲线。
图17为直流线路电压仿真结果。由图17可知:在故障发生后,正极电压由于线路切除变为0。在t=5.3 s时因重合闸改变系统拓扑结构但正极线路故障仍然存在,正极直流线路电压产生剧烈波动,重合闸失败后直流断路器再次跳开,电压波动逐渐消失。在t=5.4 s后,电压波动完全消失,正负极电压达到相对稳定状态。
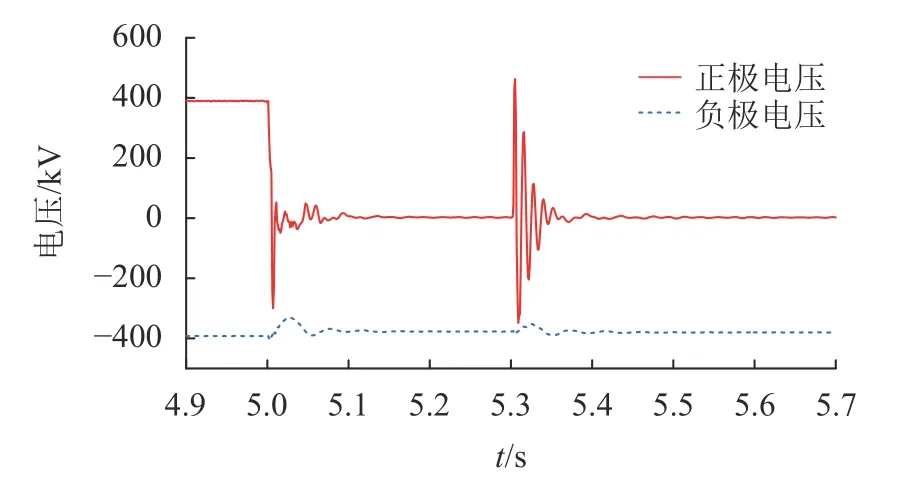
图17 换流站间直流线路电压Fig. 17 DC line voltage between converter stations
图18为电网直连换流站MMC2与风电场直连换流站MMC3故障期间功率流通情况。由图18可知:MMC2与MMC3的正极换流站有功功率在故障期间因正极线路隔离而停止与直流网络交换功率,自消纳情形下故障期间功率均由负极换流站传输,MMC2与MMC3的负极有功在经历短暂波动后变为故障前的2倍,完全承担故障期间的功率输送。在t=5.304 s后,系统因永久故障继续隔离正极线路使得拓扑结构与故障持续期间相同,因此,故障期间即为新的稳定状态,重合闸前后正负极换流站流通功率相等。
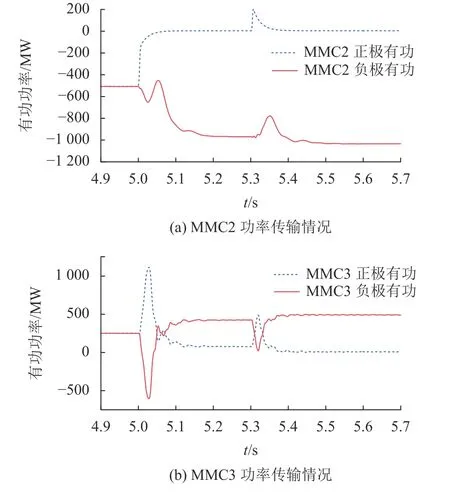
图18 换流站功率传输Fig. 18 Power transmission of converter station
图19为各换流站有功功率。由图19可以看出:各换流站有功功率在故障信号与故障类型信号发出时刻因系统结构改变发生变化,系统拓扑不再发生变化后达到稳定状态。自消纳前提下,负极换流站利用功率裕量在故障期间传输全部功率,换流站整体传输功率故障前后不变。直流断路器因永久故障重合闸失败再次跳开,重合闸前后系统稳定于相同状态。

图19 各换流站有功功率Fig. 19 Active power of each converter station
4 结 论
本文针对适用于高渗透率风电经MMC–MTDC并网系统的直流故障穿越方案开展研究。得出以下结论:
1)根据故障前系统运行状态与故障后产生的不平衡功率能否自主消纳分为不同工况,协调控制分散储能系统与风电场有功出力,改变换流站控制方式进行裕量功率消纳,所提针对不同工况采用相应的故障穿越策略,能够有效减小故障影响范围,并实现直流故障平稳穿越。
2)基于功率平衡原理的储能系统投切迅速,消纳功率数值依运行工况定量调整。仅在非自消纳永久故障情形下,当重合闸后风电场主动减小出力时出现一定情况的弃风现象,在非自消纳瞬时故障与自消纳情形下,故障前后均无能量损失。对于直流故障的单极与双极两种故障类型,本文采用的故障穿越措施均能保证在故障持续期间风机不脱网,故障后可快速恢复稳定运行状态。
本文采用等值模拟方法构建风电场,假定所有风力发电机初始状态相同,统一控制储能系统的投切,未考虑风电场中各风机出力不同的实际情况,可能会产生一定误差,这将是作者后续的重点研究内容之一。

