考虑特征值细分的广义加性短期负荷预测模型

向德军，张维静，冯歆尧，杨秋勇，蔡元纪

（1. 广东电网有限责任公司，广州 510000；2. 清华大学 电机系，北京 100084）

0 引言

随着新一轮电力体制改革的推进，电力市场化交易环境逐步形成，基于我国国情，计划与市场的“双轨制”运行方式成为当前电力市场运营的主要模式，可能导致市场电与计划电存在实际执行与合约计划不匹配、产生不平衡资金、影响市场公平有序运行等问题。准确的负荷预测可有效减少两者的偏差电量，在计划合约电量分解及市场调度运行中通过准确的负荷边界生成更贴近实际运行的调度生产计划，从而减少不同交易成分、交易时段的不匹配性。同时，准确的负荷预测还有助于建立良好的市场秩序、稳定市场电价，支撑市场主体准确预估市场收益、合理安排用电计划、制定交易策略等。

为了提升短期负荷预测精度，国内外专家和学者做了大量研究，基本预测方法分为两类:一是分析负荷时序特性，通过趋势外推进行预测，包括回归模型预测法［1—2］、卡尔曼滤波法［3］、box-jenkins法［4］等时间序列预测法；二是利用负荷随机性及趋势性的特点建立非线性映射关系模型，例如混沌灰色理论预测法［5］、基于人工智能的神经网络［6］、随机森林［7］、以及机器学习预测法［8］等。在这些方法的基础上，有学者考虑负荷易受外界因素的影响，建立了单一预测模型，包括将气象预测数据应用于负荷预测［9］，基于产业结构调整预测负荷趋势［10］，利用市场电价与负荷的关联关系进行预测［11］等，通过特定场景下特定因素的影响预测负荷整体趋势变化，预测准确度随场景波动，不具广适性。为了更全面地考虑不同因素对负荷的影响，有学者提出分层综合预测模型，文献［12］构建了温度、湿度、电价等9 个影响特征的双层多核SVM学习，文献［13—14］均设定了单一特征值预测后加和的综合模型，先利用聚类或者经验将电力负荷数据分离处理，后针对各预测分量的不同特点单独建模预测，最后组合重构形成整体预测结果。相较于单一变量预测模型，综合模型考虑因素更为全面，同样面临着更多复杂的问题，其中合理确定不同因素之间的交互影响，避免重复建模最为关键。

针对上述难题，本文提出基于影响因素相关度拆分特征值的方法，利用广义加性模型（generalized additive model，GAM）内化处理特征值之间相关性［15—17］，建立综合因素细分特征的半参数可加短期负荷预测模型，并利用最小二乘法对特征变量函数进行样条拟合，最终得到短期负荷预测值。将该方法应用于广东省2019年短期负荷预测，通过样本数据的比较，该模型预测精度良好，预测性能稳定。

1 特征值筛选及细分

在影响负荷波动的诸多变量中对短期负荷影响较大的因素可以总结为3类。一是气象类因素，包括温度、湿度、降雨等；二是日期类因素，包括工作日、周六日、节假日等；三是负荷自身波动特性。本文以广东省2018年负荷及气象资料为例，研究分析特征值。

1.1 气象特征值的细分

湿度、降雨等气象因素对负荷的影响通常通过温度体现，集中体现为夏季空调负荷、冬季供暖负荷等积温效应［18］。为了避免考虑多种气象因素导致气候影响作用叠加，本文选取温度作为关键特征值，并细分预测日前n日的逐日96 时刻温度值的特征变量，分别构建不同特征变量与实时负荷的相关模型，相关系数越大，表示该特征变量对负荷的影响越大。

相关系数采用皮尔逊函数计算，可以表示为

图1展示了广东省各地市2018年7月8日—22日实时温度的平均值与系统负荷的关系。

图1 2018年7月8日—22日负荷与温度曲线关系Fig.1 Load and temperature curves from 8th July,2018 to 22th July，2018

由图1 不难看出，两者的波动周期与幅度均展示出较为一致的步调，体现为实时温度、最高温度、最低温度与负荷相关性较强。下一步，以全年为单位，逐日逐时测算实时温度与负荷的相关系数。并考虑积温效应，测算包括前n日温度、前m时刻温度、前一日最大温度、最小温度、前7 日平均温度等指标与负荷的相关性。温度特征值与负荷的相关性系数如表1所示。

表1 温度特征值与负荷的相关性Table 1 Correlation between temperature eigenvalue and load%

受篇幅限制，表1 仅罗列了与负荷相关性超过60%的指标，筛选基于温度的细分特征变量包括实时温度、前1日最大温度、前1日最小温度、前7日实时温度以及前6个时刻的温度。

1.2 节假日特征值的细分

分析负荷曲线的波动趋势可知，节假日前后系统用电负荷较平时有所降低，在节假日期间负荷到达最低值。该特性在春节期间最为明显，春节前后的缓冲期也更长。为此，本文依据不同假期类型，首先将日期为一般节假日、春节、星期类型以及其在全年的位置分别分析，再依据影响范围筛选关键特征值。

1.2.1 节假日

考虑普通节假日以3 天假期为主，前后都是工作日，缓冲期不会太长，为此选取节日、假日、节假日前1天、节假日后1天负荷、节假日前2天、节假日后2 天负荷，分别计算各指标与其上周同类型日负荷的变化。分析结果如表2所示。

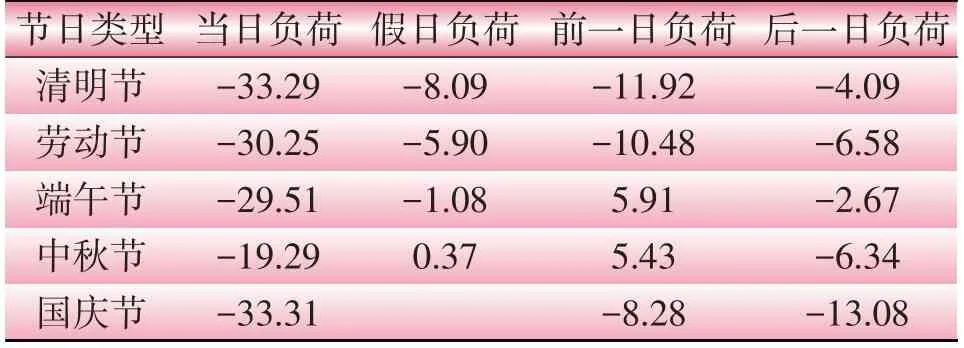
表2 不同日负荷波动对比Table 2 Comparison of fluctuations on different daily loads%

由表2可见，节假日前后负荷开始降低，节日当天负荷通常最低，假日有所缓解。因此，本文标识节日、假日（包括调休放假时间、不包括春节）、节日前1日及节日后1日作为细分节假日特征值。

1.2.2 春节

图2为2018年春节前后负荷波动情况。由图2可知，负荷从农历十二月二十开始下降，春节前后达到最低点，至正月十五回归正常用电水平。假期效应延续了25 天左右，将该时段日历划分为春节前、春节、春节后3个时段，作为细分春节特征值。

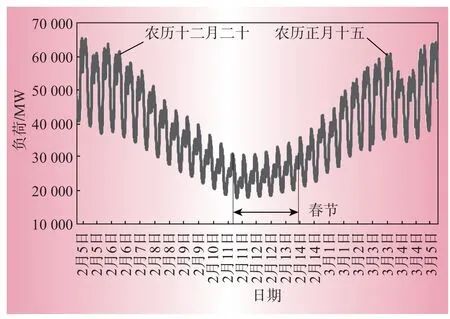
图2 2018年春节前后负荷波动Fig.2 Load fluctuation before and after the Spring Festival of 2018

1.2.3 星期类型

工作日用电负荷通常高于周末，国内外学者建立了相关模型，将工作日与周末拆分后分别预测以提升预测精度［19］,，此处不再赘述，设置星期类型特征值为星期一至星期日，分别建模。

1.2.4 日期位置

日期位置是协助锁定相似日，加强相似日之间信息耦合以提升预测精度，该思路已被广泛应用，此处不再对比计算，设置日负荷所在日期位置作为关键特征值单独建模。

1.3 负荷特征值的细分

电力负荷的变化规律对负荷未来趋势的预测具有重要影响，因此很多专家以趋势外推和时间序列类方法对负荷进行预测［20］。本文结合两类预测方法的数据训练序列，将负荷特征值分为逐96 点负荷、预测日前m时刻负荷、预测日前n日96 点负荷、预测日前1 日最大负荷及最小负荷、前7 日平均负荷等，并测算上述特征值与预测负荷的相关系数，选取相关度较高的指标作为细分特征值。

表3展示了相关系数较大的指标分析结果。根据分析，选取前1日最大负荷、前1日最小负荷、前7日平均负荷作为细分特征值。

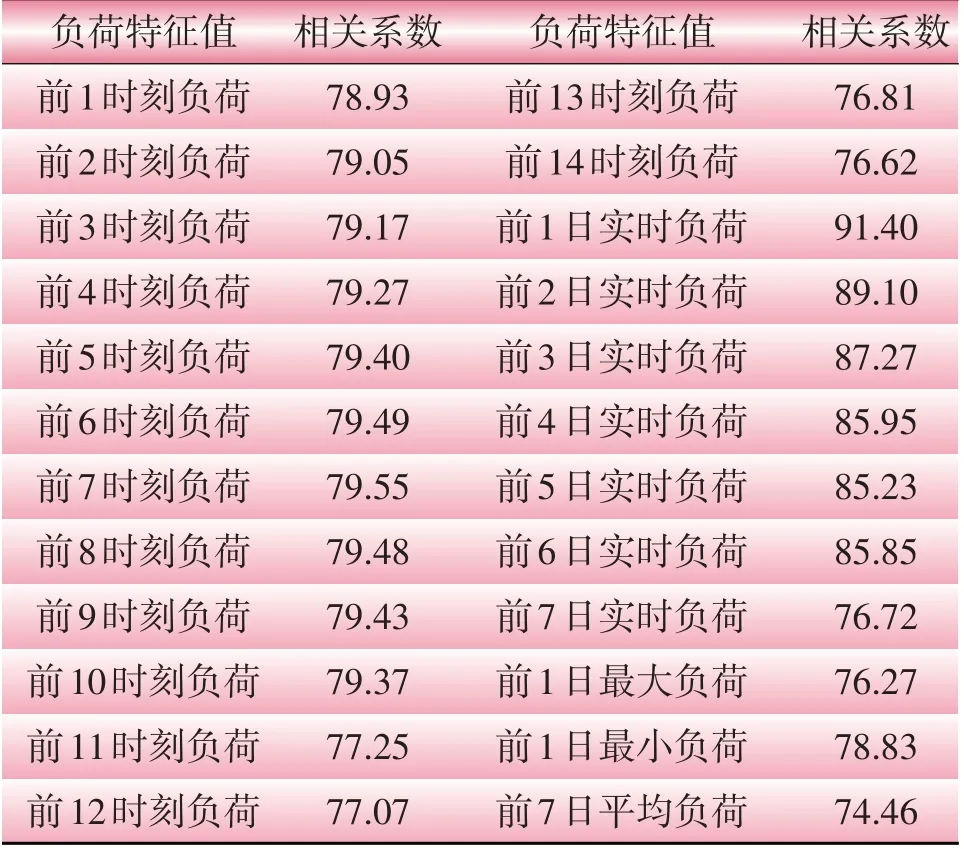
表3 负荷特征值与负荷的相关性Table 3 Correlation between load eigenvalue and load%

在滞后时刻方面，选取相关系数相对较大的滞后时刻指标作为叠加滞后影响特征值，即预测前10个时刻的实时负荷；在滞后日期方面，对比预测前n日的负荷与预测日负荷的相关性，结合负荷的星期属性，选取预测日前6日实时负荷，将两者的累计值作为负荷细分特征值。

2 GAM模型原理

GAM模型是通过“加性”的假设，将一些与反应变量间存在复杂非线性关系的预测变量以不同函数加和的形式表达并拟合到模型中［21—23］。

GAM模型的数学表达式为

式中:g(μ) 为连接函数，可依据驱动变量与预测变量之间的关系自定义函数形式；μ为期望；xi为不同驱动变量；n为驱动变量个数；f(xi)为针对驱动变量xi的单变量函数；ε为截距。

在此基础上，考虑多种复杂影响因素的短期负荷预测模型，原理如图3 所示。首先利用历史数据做相关性分析，筛选细分特征值；其次结合负荷波动特性确定基本连接函数，并初步确定特征变量影响函数以及模型参数；第三利用最小二乘法进行模型评估，将所有变量函数做拟合残差，迭代直至残差不再收敛，得到最优解。预测流程如图3所示。

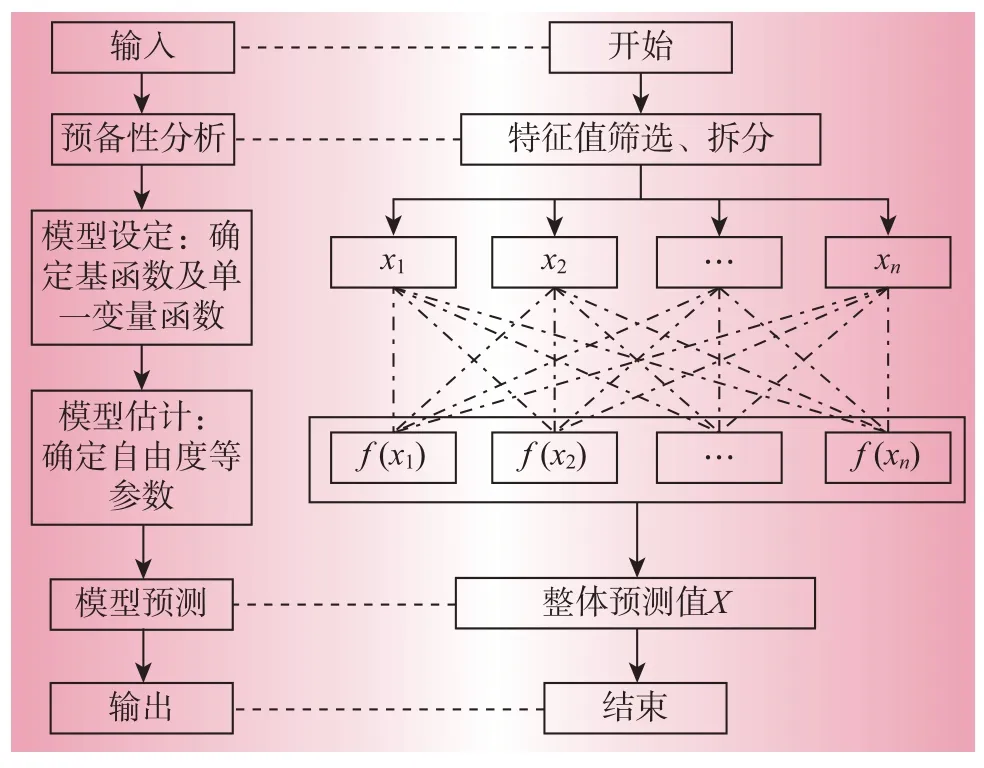
图3 预测流程Fig.3 Forecasting process

3 基于特征值细分的GAM建模

3.1 总体预测模型

考虑负荷与影响因子之间的关系具有泊松分布特性，设置对数函数作为预测模型的连接函数，整体预测模型可表示为

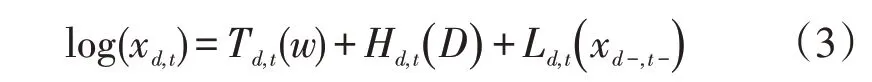
式中:xd,t为d日t时刻的预测负荷，t=1,2,...,96；Td,t(w)为温度w对d日t时刻负荷的影响；Hd,t( )D为节假日D对d日t时刻负荷的影响；Ld,t( )xd-,t-为负荷特征值对d日t时刻预测负荷的影响；xd-,t-为d日t时刻之前的负荷值。

3.2 温度特征值及模型

温度与负荷为非线性关系，利用3 次样条函数估计，温度对负荷的影响可以表示为

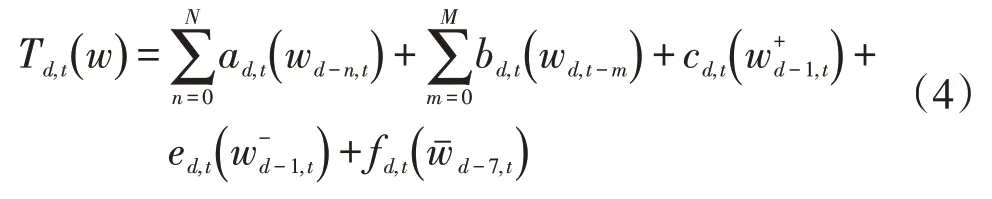
式中:ad,t、bd,t、cd,t、ed,t、fd,t分别为不同温度w对d日t时刻负荷的影响函数；n为实时温度w影响滞后天数，最大滞后天数N=7；wd-n,t为d-n日t时刻温度；m为实时温度w影响滞后时刻，最大滞后时刻M=10；wd,t-m为d日t-m时刻温度；-1,t为d-1日t时刻温度w的最大值；-1,t为d-1日t时刻温度w的最小值；wˉd-7,t为d-7 日t时刻温度w的平均值。

3.3 节假日特征值及模型

节假日对负荷的影响可以表示为

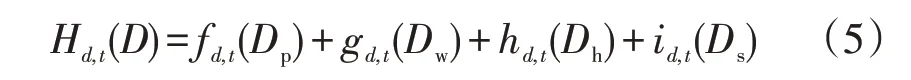
式中:fd,t(Dp)为以年为周期，负荷所在日的日历位置Dp对d日t时刻负荷的影响函数；gd,t(Dw)为星期类型Dw，包括星期一至星期日每日特性对d日t时刻负荷的影响函数；hd,t(Dh)为节假日Dh对d日t时刻负荷的影响函数，依据1.2节分析分别对节日、假日、节日前1天、节日后1天分别标识并拟合其对负荷的影响；id,t(Ds)为春节Ds对d日t时刻负荷的影响函数。所有函数使用三次样条估计，其中gd,t(Dw)的样条依据每周7天选取结点数为7。

3.4 负荷特征值及模型

负荷特征值的预测模型可表示为

式中:jd,t、kd,t、pd,t、qd,t、rd,t分别为不同负荷特征值x对d日t时刻负荷的影响函数；n为预测模型中考虑的滞后天数，最大滞后天数N=7；xd-n,t为d-n日t时刻负荷；m为预测模型中考虑的滞后时刻的最大数量，最后滞后时刻M=10；xd,t-m为d日t-m时刻负荷；-1,t为d-1 日t时刻负荷的最大值；-1,t为d-1 日t时刻负荷的最小值；xˉd-7,t为d-7 日t时刻负荷的平均值。

4 算例应用

本文以目前调度运行需要的数据颗粒，采集广东电网2016 年1 月至2019 年8 月逐日96 点负荷及温度，将数据切分为训练集（2016 年1 月至2018 年12 月逐日96 点信息）和验证集（2019 年1 月至8 月逐日96点信息），通过对验证集逐日96点负荷分别预测，并选取平均绝对百分误差（mean absolute percent error，MAPE）考量其准确率，表达式如下

式中:Preal、Ppredict分别为负荷实际值和预测值；N为数据集长度。

为进一步对比该模型的优劣，选取人工神经网络模型（artificial neural network，ANN）以及不考虑精细化特征变量的综合预测模型分别针对温度、节假日、负荷特征值建模，生成各月平均MAPE 误差见表4。其中，ANN 模型采用包括输入层、隐含层和输出层的BP神经网络，输入层各输入单元分别为本文第1节选出的细分特征变量，隐含层和输出层采用sigmoid激活函数，经过网络学习训练调整权重和预测计算后，输出2019年1月至8月逐日96点负荷预测值。综合对比看出，基于特征值细分的GAM 模型MAPE误差为0.017 9，优于其他两种方法。

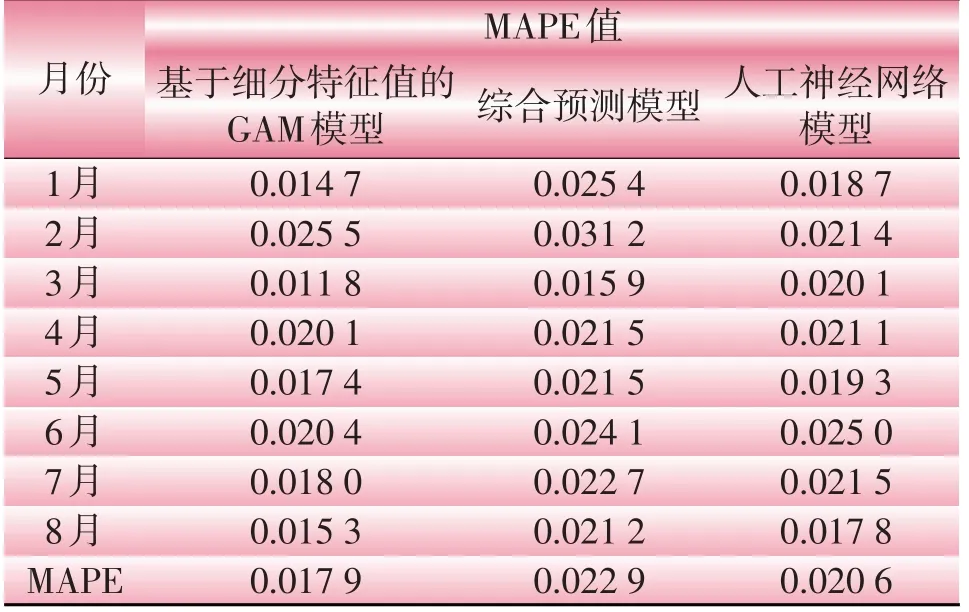
表4 不同预测模型的MAPE值对比Table 4 Comparison of MAPE values for different predictive models

此外，区别于神经网络“黑匣子”预测体系，GAM模型可进一步量化分析不同特征变量对负荷的影响，以协助用户调整、完善特征变量，提升预测精度。

节假日对负荷的影响选用estimate估计法，estimate 越接近于0，表征该特征变量对预测负荷的影响越大。节假日特征变量对负荷的estimate 估计如表5所示，春节与星期特性是影响负荷波动的关键。

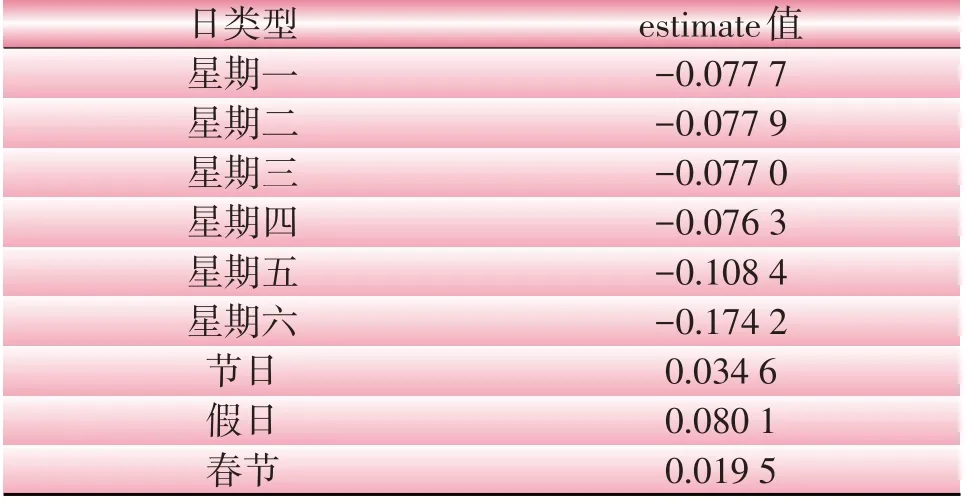
表5 节假日特征变量对负荷的estimate估计Table 5 Estimate of characteristic variable to load during holidays

图4以典型日某一时刻为例展示了星期类型、实时温度与预测负荷的三维关系。同一温度下，星期一、星期二的负荷更高，星期三呈现拐点用电需求开始下降；同一星期类型下，实时负荷随着温度升高而升高。

5 结束语

负荷预测作为关乎发、用电平衡的基础，对支撑电力市场稳定运行、保障市场主体经济利益有着重要的意义。本文针对综合预测模型难以厘清变量间交互影响的问题，提出在常规特征值基础上进一步细分特征变量，并基于GAM模型内化处理不同因素的交互作用，形成考虑特征值细分的广义加性短期负荷预测模型。通过实际算例表明，相较综合预测模型及神经网络模型，该方法预测精度更优，且可直观展示各细分特征值对负荷的影响，为进一步支撑特征值筛选和预测模型调优提供了有效依据。随着电力市场深化，模型中可增加考虑电动汽车、市场电价等特征变量，进一步完善预测理论和模型，为提升负荷预测精度提供支撑。D