一种光学单站姿态处理二义性正确解确定方法

胡小丽，唐明刚，蔡文泽，吴海英，张思琪，张三喜

（1. 华阴兵器试验中心，陕西 华阴 714200；2. 西安现代控制技术研究所，陕西 西安 710065）

引言

按照物像成像方式的对称性，光学单站姿态处理难以避免处理结果的二义性，因判读误差、其它输入参数测量误差耦合原因，处理结果并不会出现多解现象，优化处理结果通常处理为单解形式，除粗大误差外，数据趋势结果多表现为分段显著的2 种变化趋势，如何通过单站序列图像姿态处理结果，将正确二义解解算出来，一直是单站姿态处理的固有难题。查阅大量单站姿态处理及姿态处理文献[1-15]，尚未见二义性修正相关报道。

本文以基于直线矢量的物像映射关系为基础，从单站姿态处理结果着手分析数据结果曲线规律，根据曲线变化趋势确定整体正确解，之后对局部错误二义性解进行修正，后反向变换至基准坐标系中获取求解时刻特征矢量空间矢量，对矢量进行解析获取正确姿态解。

1 算法分析

1.1 目标主体直线矢量选取依据

目标坐标系主体架构，分别是目标中轴、目标尾翼以及与前两者垂直的目标特征，这3 者可作为直线矢量选取的3 个矢量基，分别是e1(1 0 0)T、e2(0 1 0)T、e3(0 0 1)T，其他目标直线矢量均可由这3 者组合而成。按照姿态处理通常坐标系定义，3 个矢量基由初始零姿态向求解时刻姿态旋转为（e1＇e2＇e3＇)，有：

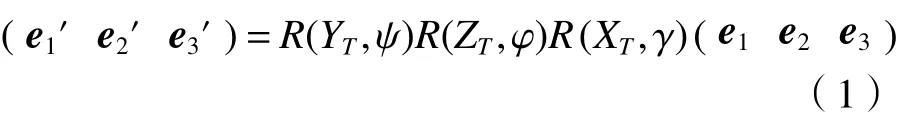
式中：R为姿态旋转过程中涉及的矩阵。

由（e1＇e2＇e3＇)中涉及的姿态角可获得各类直线矢量涉及的姿态角信息，为后续特征直线矢量选取提供依据。

1.2 单站姿态处理算法关键步骤分析

1） 能表征需求姿态角的关键直线矢量选择，如中轴、尾翼等直线矢量；

图1 单站直线矢量姿态映射图示Fig. 1 Diagram of pose mapping for single-station straight line vector

坐标系说明：所有涉及坐标系以常规姿态处理算法中涉及的坐标系为基准。其中目标坐标系以目标中轴为XT轴，头部为正；基准坐标系以北向为X轴；摄像机坐标系以光轴指向为XC轴，平行于像面向上为YC轴；像面坐标系y、z轴分别平行于像机坐标系YC轴、ZC轴。

1.3 单站姿态处理二义性正确解获取

取典型目标关键直线矢量向像面映射的俯视图进行二义性说明，2 类目标共处于摄像机坐标系下进行投影变换，左侧为弹类目标，以中轴作为其关键矢量；右侧为飞机类目标，以中轴矢量和尾翼矢量作为其关键矢量；2 种目标相对ZC轴呈完全对称模式，故相对像面成像状态完全等效，若出现解的二义性，必为此环节所致。弹类、飞机类目标相对像面投影二义性说明，如图2 所示。

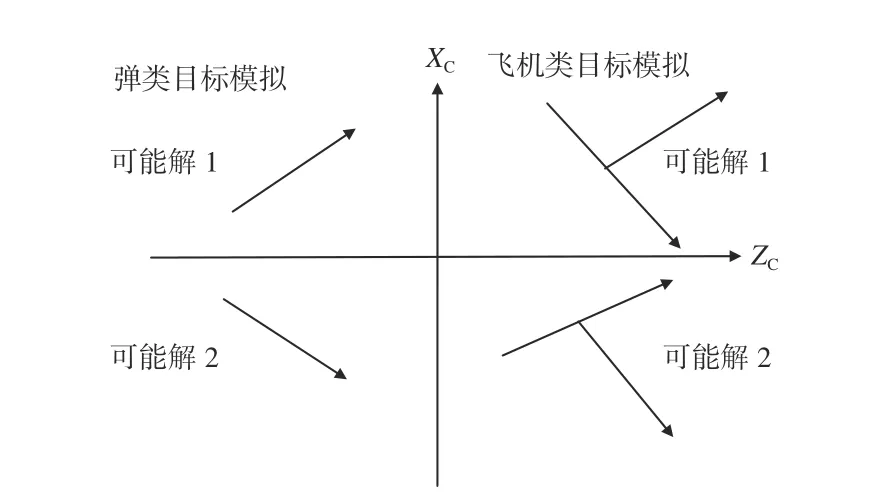
图2 弹类、飞机类目标相对像面投影二义性说明Fig. 2 Ambiguous description of projection to image plane of missile and aircraft targets

根据1.2 单站姿态处理算法关键步骤分析，可知光学单站姿态测量二义性，实质是目标关键矢量相对于摄像机像面投影的对称性，按照常规姿态测量坐标系定义，则实质是目标关键矢量在X方向的分量相对于摄像机像面投影的对称二义性。基于姿态测量关键矢量物像映射及空间重构过程，本文提出了二义性正确解获取流程。单站姿态处理二义性正确解修正步骤，如图3 所示。

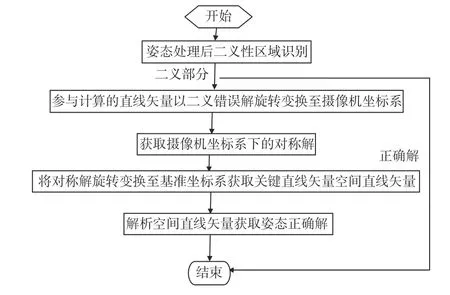
图3 单站姿态处理二义性正确解修正步骤Fig. 3 Modified steps of ambiguous correct solution of single-station pose processing

以弹类轴对称回转体目标为例，具体分析过程如下：

1） 对单站序列图像姿态处理结果（偏航角ψ、俯仰角φ）进行分析，数据变换趋势总体趋势为正确解趋势，其中局部集合存在单站姿态处理的二义性解；

2） 主流变化趋势保留，根据二义性错误解反向推断正确解，按照1.3 节所述，必须将此二义解由基准坐标系变换至摄像机坐标系下反向推算正确映射结果，代入单站姿态处理二义性错误解（偏航角ψ、俯仰角φ）和光轴指向（A E），将中轴矢量（1 0 0）T由求解时刻状态L(cosψcosφsinφsinψcosφ)T向摄像机坐标系变换映射得到Lc（lCmCnC）T；

3） 将Lc（lCmC nC）T修正为Lc＇（-lCmC nC）T；

4） 将Lc＇（-lCmC nC）T反向变换至基准坐标系，得中轴矢量求解时刻正确解L＇(l m n)T；

5）解析L＇(lm n)T，获取正确解ψ＇、φ＇。

飞机类则按照中轴矢量流程增加尾翼矢量，解析3 个姿态角。

主成分分析是一种降维的多源统计方法，利用多个具有相关性的线性组合解释多维变量，从中寻找最佳变量，简化数据量[10]。主成分分析基本思想是根据相关性大小把变量分组，使得同组内变量之间相关性较高，但不同组变量相关性较低，并试图用较少个数公共因子的线性函数和特定因子之和来表达原来观测的每个变量，以达到合理解释存在于原始变量间的相关性和简化变量维数的目的[11-12]。

2 算法验证

2.1 平飞段二义性修正

实验航线姿态设置及布站：某飞机沿主靶道近似平飞；机上有遥测位置姿态数据；分站1#布设于飞机弹道侧方，其中X，Z分别为：（3 500 m，-1 500 m）；飞机飞行航迹与飞行姿态参数：X（4 400 m～6 600 m），Z（295 m～37 m），Y（1 182 m～1 184 m），Ψ（-7.3°～2.3°），φ（-0.6°～2°），γ（-3.5°～8.6°）其中，Y、Ψ、φ、γ均为量值变化范围，变化过程随飞机飞行过程呈现非均匀起伏状态。

处理条件：分别提取飞机中轴和尾翼直线特征，各边成像以通常定义的目标体坐标系为依据，分别为中轴（178 pixs～48 pixs）、尾翼（451 pixs～338 pixs），其中中轴线性特征良好，尾翼线性特征一般。

如图4 所示，单站姿态测量数据总体与遥测数据吻合良好，由于判读误差的随机性，存在一定的随机误差。需要注意的是，3 个姿态角的起始段落，同步相对遥测数据有明显偏差，考虑处理算法的影响因素，定位为二义性错误解。

图4 飞机姿态数据处理-平飞Fig. 4 Data processing of aircraft in level flight attitude

按照1.3 节对上述数据进行二义性修正。

从图5 可知，相比于图4，与遥测数据对比差异明显减少，整体更多体现的是判读误差的随机性。相对误差均方根指标二义性修正前后如表1所示。

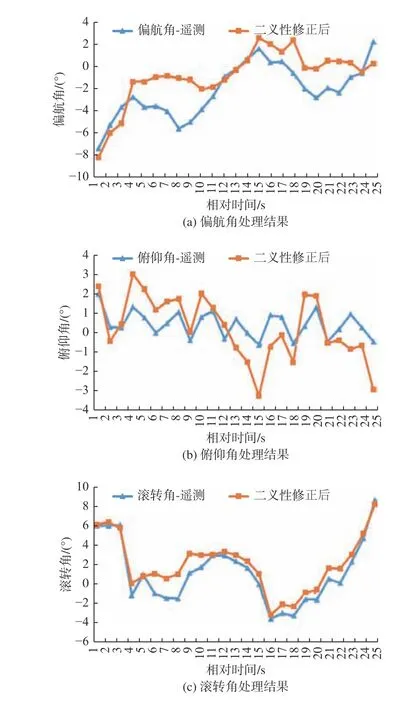
图5 飞机平飞段姿态数据经二义性修正后处理结果对比Fig. 5 Comparison of processing results of aircraft attitude data in level flight after ambiguous modification

表1 进一步说明，二义性修正前后相对遥测结果差异明显，精度量级得到了显著提高。

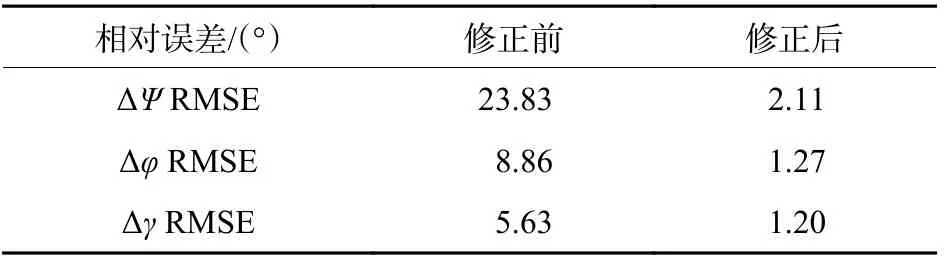
表1 二义性修正前后结果指标对比Table 1 Comparison of outcome indexes before and after ambiguous modification

2.2 终点段二义性修正

实验航线姿态设置及布站：为验证算法正确性，将某型飞机沿参考系X向飞行0～3 km，其中偏航角设置为5°以内，俯仰角设置为2°～18°～12°先升后降，滚转角控制在正负5°内。为保证算法二义性校正结果对比，设置交会测量条件，将姿态测量系统（2#、3#）布设于飞机侧方，保证航线内交会结果满足精度基准要求；

处理条件：采集图像后，采用交会及2#单站同时进行姿态处理，其中2#单站基本处于目标航线斜侧方，基本保证了目标飞机轮廓三角的稳定性，为后续特征准确提取奠定基础。分别提取中轴及三角形三边，各边成像以通常定义的目标体坐标系为依据，分别为中轴（215 pixs～246 pixs）、右侧（123 pixs～160 pixs）、尾翼（149 pixs～168 pixs）、左侧（130 pixs～165 pixs）、单站。

按照1.1 节进行处理，截取其中一段数据，处理结果如图6 所示。

数据说明：

1) 单站多站数据趋势大体一致；

2) 3 姿态角的局部段落，同时相对多站有明显偏差，定位为二义性错误解。

按照1.3 节对上述数据进行二义性修正。

从图7 可知，相比于图6，交会与单站处理结果差异明显减少，3 个姿态角的误差更多体现为判读误差引发的不同步随机性误差。相对误差均方根指标二义性修正前后如表2 所示。

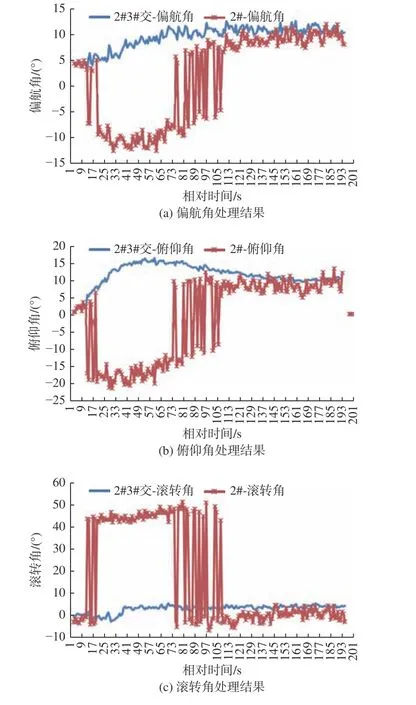
图6 飞机姿态数据处理Fig. 6 Data processing of aircraft attitude

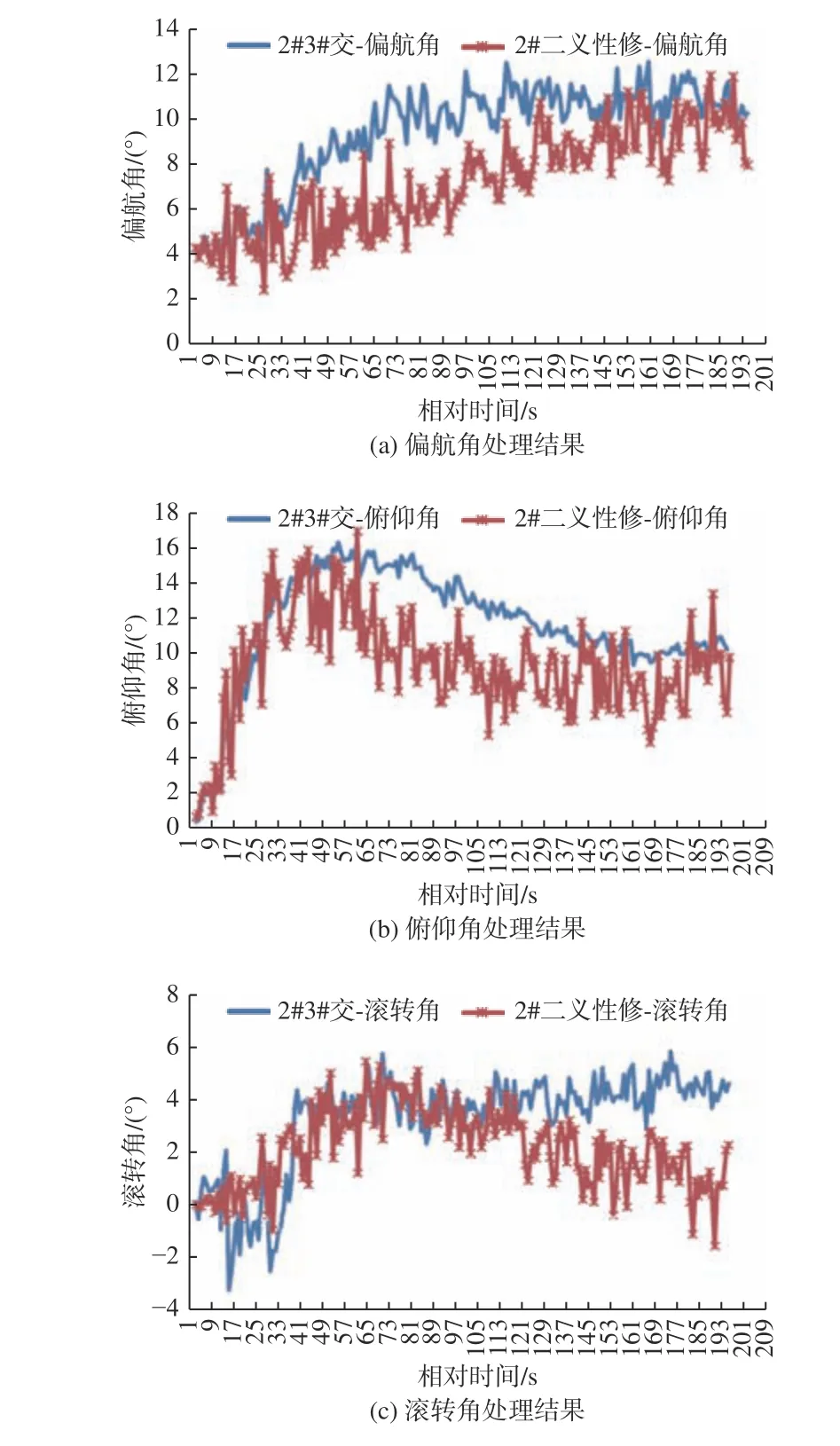
图7 飞机姿态数据经二义性修正后处理结果对比Fig. 7 Comparison of processing results of aircraft attitude data after ambiguous modification

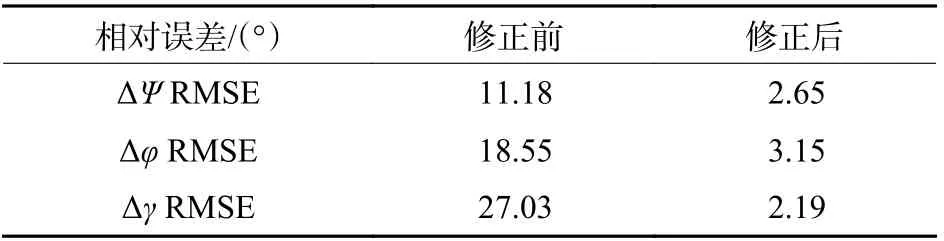
表2 二义性修正前后结果指标对比Table 2 Comparison of outcome indexes before and after ambiguous modification

表2 进一步说明，二义性修正前后相对交会处理结果差异明显，精度量级得到了显著提高，达到了修正目的。

3 总结

本文以承载姿态的主要矢量为分析对象，根据姿态处理结果分析整体正确解趋势和局部二义性错误解，按照姿态变换关系，对直线矢量进行中间环节映射修正，后反向变换至基准坐标系中获取求解时刻矢量状态，并根据姿态旋转矩阵姿态承载关系解析获取正确姿态解，为实际轴对称回转体和非轴对称回转体目标单站光学姿态处理获取可靠的二义性正确解提供理论依据。