一种基于双馈风机锁相环动态响应的风-火协同调频策略

崔幼石，严干贵，刘櫂芮，贾希浩，王振洋，翟文超

（东北电力大学现代电力系统仿真控制与绿色电能新技术教育部重点实验室，吉林吉林 132000）

0 引言

“双碳”目标驱动下，我国新能源渗透率将稳步提升，风力发电是新能源发电的重要组成部分[1]。截至2021 年5 月，全国风电机组累计装机容量已达到2.9×105MW；而到2050 年，这一数字预计将达到2.4×106MW[2]。

风电等新能源设备在系统发生功率不平衡扰动时不响应系统的频率变化，而大规模风电并网必然会降低系统频率稳定性[3-6]，因此需要风电场在备用一定功率的基础上，具备参与系统一次调频能力。目前各国出台的新能源并网准则均要求新能源场站能够参与系统一次调频[7-10]。

双馈风电机组（Doubly-fed Induction Generators，DFIG）在减载控制的基础上对于系统频率可以提供一定的支撑[11-15]，文献[16-19]提出了场站中各个机组下垂系数的整定方法，使风电机组能够更有效调频功率，在频率扰动时提供可靠的功率支撑。文献[20]针对微电网稳态频率偏差进行优化，提出变减载率的方法，通过优化算法得到最佳下垂控制参数，文献[21]基于模糊逻辑算法提出了提升电网频率控制效果的速度控制器动态运行算法，缓解了与调频环节间的相互矛盾作用。本文主要工作在于研究双馈风电机组运行在最大功率点跟踪（Maximum Power Point Tracking，MPPT）下的惯量控制及分析控制参数对其惯量特性影响。

风电的惯量控制是在惯性响应阶段在并网逆变器控制环节上附加信号，以使风电机组模拟传统同步机在面对负荷扰动时释放旋转元件动能，阻止系统频率变化过快而影响电网稳定运行[22]。文献[23]量化了DFIG 在暂态过程中可提供的最大有功支撑，并在电力系统建立了风电机组频率支撑能力与频率优化的相互关系，并量化分析了风电短期功率支撑作用下对系统频率跌落值的提升效果。在转子惯性响应的支撑能力分析方面，文献[24]则评估了定速型风机和变速型风机在系统中的惯量支撑能力，变速风机的转子速度可在变流器的控制作用下降到更低，由此可以为系统提供更多的功率支撑。文献[25]提出了一种通过需求层次分析模型，对于目标函数中各指标的参与因子进行优化，进而对机组参数进行优化选择的策略。

现有研究基本着眼于对风力发电机附加控制使其具有惯量响应的能力，以及对传统惯量控制方式参数的优化方面，对于风电设备惯量特性的本质以及其参与调频过程中与所在系统中与同步机一次调频的相互影响鲜有研究。

本文以双馈风电机组为对象，研究了双馈风电机组的结构及控制系统，基于锁相环动态响应原理，研究锁相环参数对双馈风电机组惯量特性的影响，分析风电惯性控制与同步机一次调频之间的交互作用，并提出风电转子惯性控制与同步发电机一次调频协同优化控制策略，为新能源设备参与系统一次调频提供优化帮助。

1 双馈风力发电机建模

本文所采用的DFIG 机组如图1 所示，由多个风力机、双馈感应电机、四象限变流器及线路负荷参数构成[26]。

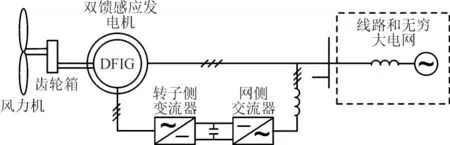
图1 双馈风电机组并网结构图Fig.1 Grid connection structure of DFIG

以功率外环控制指令控制转子侧变流器，可以实现定子有功与无功解耦控制，而网侧变流器的功能是控制逆变器直流电压稳定并辅助转子变流器调节并网有功、无功功率，其基本控制框图如图2所示。Ps和Qs为机侧变流器有功和无功功率，Pb和Qsref为对应的有功/无功参考功率，udc与Qg为逆变侧直流母线电压与网侧无功功率。Usq/d，Urq/d，Ugq/d分别为定子、转子、网侧q/d轴电压，isq/d，isq/d，igq/d分别为定子、转子、网侧q/d轴电流，下标ref 表示对应参考值。Ud为并网点电压的d轴分量，S为转差率，xm与xs分别为励磁电感与定子漏抗。ωr为转子角速度，ωg为网侧同步角速度，Ls为定子侧电感，Lf为网侧滤波电感，ura，urb，urc为机侧变流器输出的a，b，c 相电压，uga，ugb，ugc为网侧变流器输出的a，b，c 相电压。

图2 双馈风电机组四象限变流器控制系统Fig.2 Four-quadrant converter control system of DFIG

建立双馈感应电机数学模型，规定定子电压，电流方向为发电机惯例；转子电压、电流方向为电动机惯例，以定子合成磁场矢量方向为d轴，建立dq两相同步旋转坐标系，ψsq/d，ψrq/d分别为定子侧与转子侧的q/d轴磁链；ω1，ωs分别为同步角速度和转差角速度；Rs，Rr分别为定子侧与转子的等效电阻，其中ψsd=0，ψsq=-ψs。Usd=Us，Usq=0。

dq坐标系下双馈感应电机定、转子电压方程为：

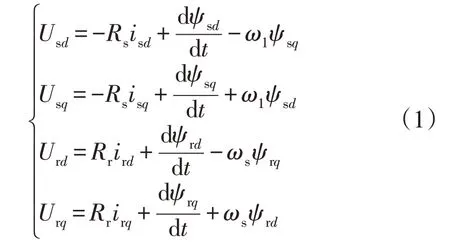
定、转子磁链方程如式（2）所示。

式中：Lr为转子侧电感；Lm为定转子之间互感。

2 双馈风力机组转子惯性控制策略

传统运行模式下，双馈风机一般运行在MPPT运行点处，在一个稳定的风速值下时，其捕获的机械功率已达最大值，在系统内发生功率缺额产生向下的频率扰动时，并不能如传统的同步发电机一样通过调速器控制气阀开度以增发功率为系统提供有功支撑。

因此，双馈风机持续参与系统频率调制势必放弃最大风能捕获，留有部分有功备用，其典型的减载方式分为两种，一种是中低风速下使风力机组运行在超速减载运行点，另一种是在高风速下增大桨距角，此两种方法的控制逻辑都为让风力机运行偏离MPPT 运行点，减小其风能利用系数Cp 以减少风能的捕获量，在系统需要双馈风电机组参与频率调制时，调整DFIG 运行点以增大风能捕获量，释放有功备用。

事实上，采用超速减载与桨距角减载两种方法提供的备用功率较为有限，且会造成弃风、弃电问题，影响风力发电机组的经济效益。本文聚焦于采用转子惯性控制，既使得风电处在MPPT 运行状态下，又能保证其在系统发生调频需求时能提供暂时的功率支撑，并提出双馈风电机组惯性控制下与系统中同步发电机的协同控制策略，进一步优化系统功率扰动下的频率特性。

2.1 基于锁相环动态响应过程的惯性控制设计

对于同步机组而言，有转子运动方程

式中：PGm为同步机机械功率；Pe为同步机电磁功率；H为惯性常数；ω为同步机角速度。

同步发电机组惯量响应阶段，系统出现功率缺额后，如式（4）所示，由于发电机励磁电压与机端电压的相位差在系统扰动作用下发生了改变，进而导致电磁功率增加，而此时调速器尚未响应频率变化，同步机机械功率仍保持不变，轴系元件在不平衡转矩的驱使作用下按转子运动方程发生转速变化以释放动能。

式中：E为发电机励磁电压；U为机端电压；X为发电机等效电感；δ为发电机励磁电压与机端电压的相位差。

同样，双馈风力发电机组的旋转元件中蕴含着巨大的旋转动能可由式（5）表示：

式中：Er为在任意转子转速Ω（rad/s）下储存在风机转子中的旋转动能；J为风力发电机组旋转元件的转动惯量。

在风力机转子转速发生变化时释放或吸收的功率ΔPinertia可表示为：

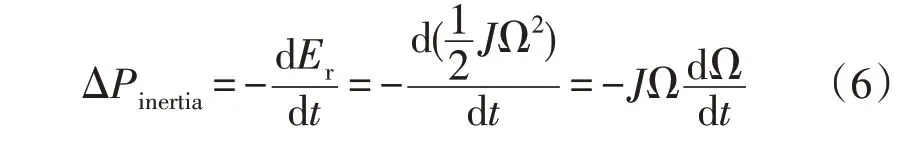
而在转子转速发生变化时，忽略损耗，风电机组因转速偏离最大运行点会导致捕获机械功率变化，偏差值为ΔPm，在该过程中风机定子功率Ps值可由式（7）表示：

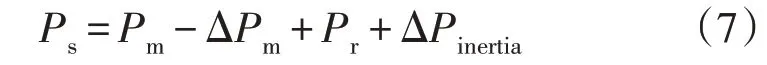
式中：Pm为风电机组捕获的机械功率；Pr为转子功率。

DFIG 对外实际增发的功率为ΔP，其表达式为：

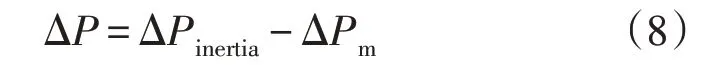
风电机组较传统的惯量控制如图3 所示，V为当前时刻风速，k为惯量控制增益系数，f为系统频率，其逻辑为在DFIG 有功控制环中引入系统频率偏差量和微分量，使系统频率与风电转子转速与之间产生耦合关系，系统频率发生跌落时，定子功率参考值Pb突增，风力发电机的电磁转矩增加控制转子减速，从而让存储在风力机旋转叶片中的部分动能转化为电磁功率以补充功率缺额，Ps随之突增为电力系统提供短暂的功率支撑。这种典型的控制方法本质在于通过附加参考信号使DFIG 内部机械部分与电磁部分产生不平衡功率，使其模拟同步发电机的惯量响应。其缺点在于需时刻监测风电机组并网点频率变化微分量，并且改变了风力发电机组的控制结构，且增益系数k的整定原则设计十分困难。

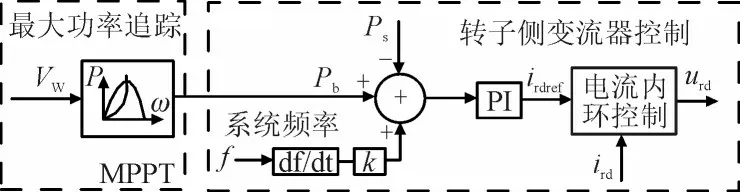
图3 传统风电虚拟惯量控制策略图Fig.3 Diagram showing traditional wind power virtual inertia control strategy

2.2 基于锁相环响应的惯量控制策略

基于文献[27-28]所提出双馈风电机组频率响应模型，评估双馈风电机组惯量特性及对系统频率特性影响。忽略电磁暂态过程，将锁相环坐标系下定子电压磁链方程简化为：

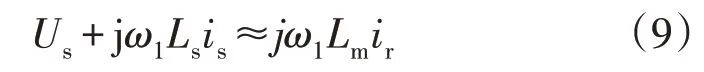
相较于同步发电设备内电势的概念，定义E=jωLmir为双馈风电机组内电势，锁相环坐标系下，内电势E，电网电压Ug，双馈风机端电压Us以及在扰动后的端电压相位U′s，网侧变换器的相位角为θs，锁相环锁相相角为θPLL，相位关系如图4 所示。

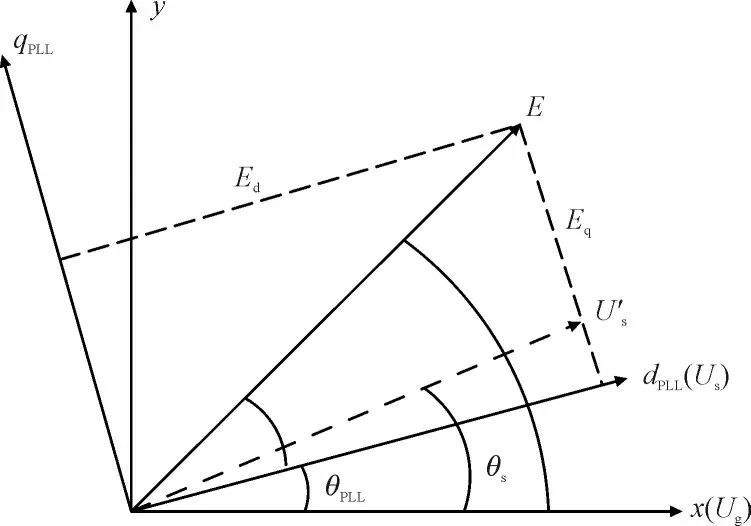
图4 锁相环坐标系下DFIG内电势相位示意图Fig.4 Schematic diagram of internal voltage phase of DFIG in PLL coordinate system

对于风电等新能源设备而言，经锁相环并网，系统频率受扰动变化时，在锁相环的相位追踪作用下不响应系统频率扰动本质是网侧变换器内电势与电网电压的快速锁相会导致系统发生功率缺额时的θs近乎不发生改变，风电机组输出的电磁功率不受电网扰动影响。

采用图5 所示的锁相环控制策略，通过合理设置双馈风电机组网侧锁相环控制参数，能够放缓网侧锁相环锁相速度，进而使系统频率扰动时θPLL能够发生改变，风电进而在系统扰动作用下响应锁相环功角变化，由此模拟同步发电机惯量特性，等效增加其在系统发生功率扰动时中所体现的惯量水平。

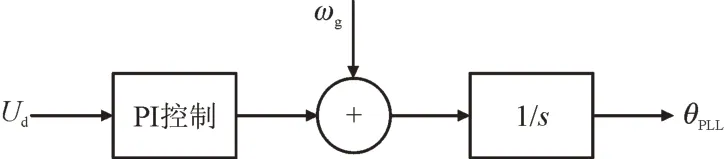
图5 锁相环控制策略Fig.5 PLL control strategy

基于锁相环快速响应特性的风机惯量控制策略，其优点在于无需附加控制策略，也无需时刻监测系统频率变化量及微分量，利用锁相环内电势相位差，能在电力系统发生功率扰动的同时，瞬时释放风力机轴系储存的动能，而其支撑时间尺度较长，与同步发电机一次调频时间尺度会有重叠，大量的风电机组旋转能量释放会抑制同步发电机一次调频的作用。

3 风-火协同调频策略

3.1 风电惯量响应对同步机调频抑制作用分析

同步发电机参与电力系统一次调频的原理如图6 所示，TCH为高压缸气室蒸汽容积时间常数，TRH为中间再热管蒸汽容积时间常数，KG为转速调节器的放大系数，TSR为继动器时间常数，TSM为油动机积分时间常数，FHP为高压缸功率系数。其调频原理在于系统频率发生偏差时，通过调速器给出调频信号影响同步发电机气门开放程度改变自身出力以响应系统频率发生的变化。

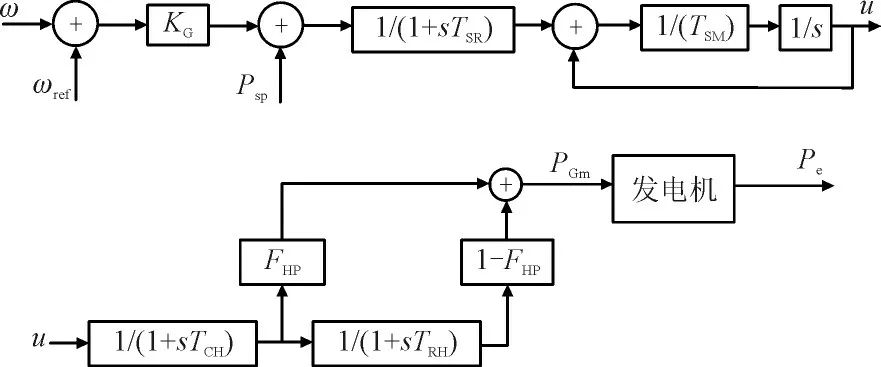
图6 同步发电机调速器及原动机数学模型Fig.6 Mathematical model of synchronous generator governor and prime motor

图7 为本文所采用的再热式同步机组频率响应模型。采用双馈风电机组惯量控制策略的同时风电机组对电力系统的快速功率支撑功率较大，支撑时间尺度较长，对同步发电机而言相当于暂时减少了系统中的不平衡功率，即减小了PGm与负荷功率PL的差值，由式（11）可知，减少PGm与PL的差值会导致Δωg绝对值减小，Δωg本身为负值，调速器反馈作用后同步机参与调频的增发功率暂时减小。

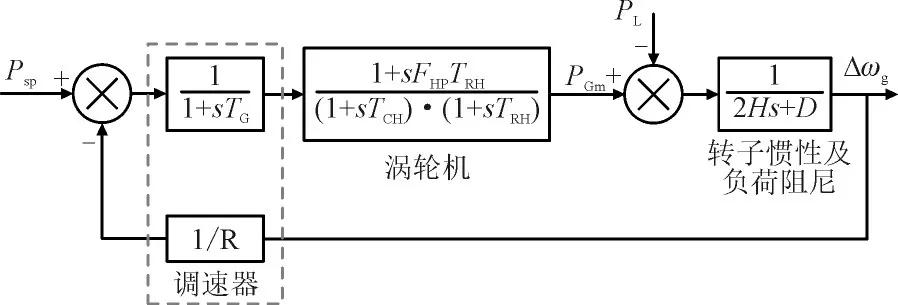
图7 再热式同步机组频率响应模型（SFR）Fig.7 Frequency response model of reheat synchronous generators

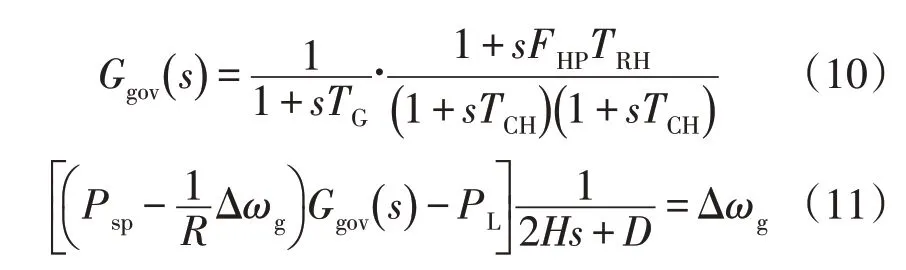
式中Ggov（s）为涡轮机传递函数。

如图8 所示，fa为扰动发生前的系统频率；PO为扰动发生前的同步发电机出力值；PL为扰动发生前的负荷特性曲线；f′a为风电机组惯量响应支撑效果结束时的系统频率；P′O为风电机组惯量响应支撑效果结束时的同步发电机出力值；P′L为风电机组惯量响应支撑效果结束时的负荷特性曲线；f″a为风电机组惯量响应支撑效果最强时的系统频率；P″O为风电机组惯量响应支撑效果最强时的同步发电机出力值；P″L为风电机组惯量响应支撑效果最强时的负荷特性曲线。不计负荷自身的频率调节效应，系统负荷增加量为ΔP时，同步发电机组的一次调频目标出力应由PO向P′O移动，而此时不平衡功率出现的同时风力发电机组产生惯性响应，对于同步机组而言，由于风电机组的快速响应提供了一部分功率支撑，此时系统中的不平衡功率等效减少，负荷特性由P′L向P″L处移动，同步机一次调频目标出力点则由P′O偏移至P″O。

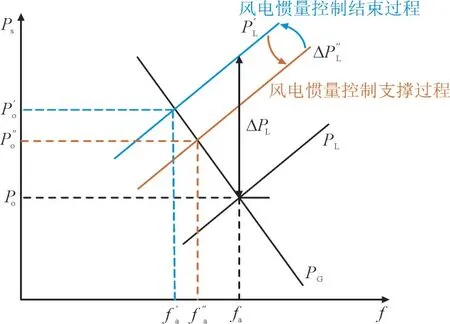
图8 风电惯量控制下同步发电机一次调频特性图Fig.8 Primary frequency regulation characteristics of synchronous generator under inertia control of wind power

而在风电转子惯性控制减弱直至结束时，负荷特性线又重新向着P′L处偏移，最终回到P′L处，同步机调频目标出力点再次回到P′O处，在这个过程中，风电机组的惯量控制虽短暂提供了功率支撑，但对于系统频率稳态值并不起优化作用，却在惯量支撑过程中抑制了同步机组一次调频出力。

3.2 风电场主导的调制信号设计

在基于锁相环动态响应的风电转子惯性控制策略的基础上，提出一种与同步机组协同频率响应控制策略，旨在使风机在响应系统频率变化大量释放旋转动能的同时，提高系统中同步机组调速器的响应速度，减弱非同步机能源参与系统惯量响应对同步机一次调频的抑制作用，进一步提高系统频率稳定性。

在风力发电机的惯量动态响应过程中，同步发电机调速器所接收到的一次调频信号会等效减小，本文所提出的策略的原理在于利用与风力发电机的惯量支撑功率相耦合的调制信号时刻对同步发电机组调速器的一次调频信号进行修正补偿。

为使同步发电机组调速器在风电机组惯量响应的同时加速响应，首先需获取与风力发电机的惯量支撑功率相耦合的调制信号。在系统频率动态过程中，双馈风电机组采用基于锁相环动态响应的惯量控制策略的优点在于响应过程中无需改变风电机功率外环参考指令值Pb，该指令值近乎一直处于稳态时所设定的该风速下最大运行点而不发生改变。

如图9所示，在风电机组惯量响应阶段，Ps1为风电场内第1 台风力机组定子实时输出功率；Pb1则为第1 台风电机组功率外环参考值指令值；Psi为风电场内第i台风力机组定子实时输出功率；Pbi则为第i台风电机组功率外环参考值指令值；将Psi与Pbi实时作差后可获取风电机组对外惯量支撑功率ΔPi。该信号能近似反应风电场中本台风力发电机组的转子惯量支撑动态过程下对外增发的功率大小以及时变特性，而实际风电场中各机组工况具有差异性，为反应扰动期间风电场整体惯量支撑水平，取所有风电机组对外增发功率平均值作为风电场主导的上层调制信号Porder，如式（12）所示。

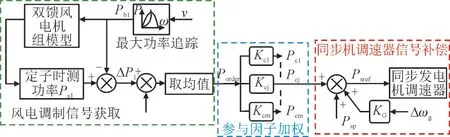
图9 风-火协同控制策略图Fig.9 Diagram showing wind-thermal power cooperative control strategy

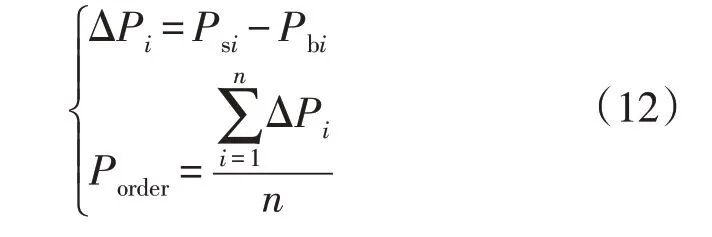
考虑系统内风电场规模对同步发电机组的影响，在对同步发电机组附加修正信号前，对协调控制信号Porder进行加权。设共有m台同步发电机组采用该调频策略，Kc1为第1 台同步发电机组参与协调控制的权重参与因子；Kcj为第j台同步发电机组参与协调控制的权重参与因子；Kcm为第m台同步发电机组参与协调控制的权重参与因子；Pc1为对第1 台同步机组下发的修正信号；Pcj为对第j台采用协同控制策略的同步机组下发的修正信号；Pcm为最终给第m台同步机组下发的修正信号。

式中：SDFIG为采用锁相环惯性控制的风电场总装机容量；SSGj为第j台采用协同控制的同步机组额定装机容量。

最后，将加权后的调制信号Pcj作为下层补偿信号发送至对应同步机组调速器控制系统，以保证风电机组因惯性响应快速增发功率导致同步机组一次调频信号减弱的同时控制系统下发的信号Pcj会对同步发电机组调速器进行正向的调频信号补偿，从而加速同步发电机调速器响应。

4 算例分析

在EMTDC/PSCAD 电磁暂态仿真软件中搭建如图10 所示的三机九节点算例仿真系统，包含3 台容量为900 MW 的同步机组（G1，G2 和G3），实际出力为450 MW，在母线5 处馈入采用容量加权的单机倍乘等值方式构建的装机容量为1 050 MW（1.5 MW×700）的风电场，此时风速为8 m/s，双馈风电机组和同步机组参数如表1 和表2 所示。

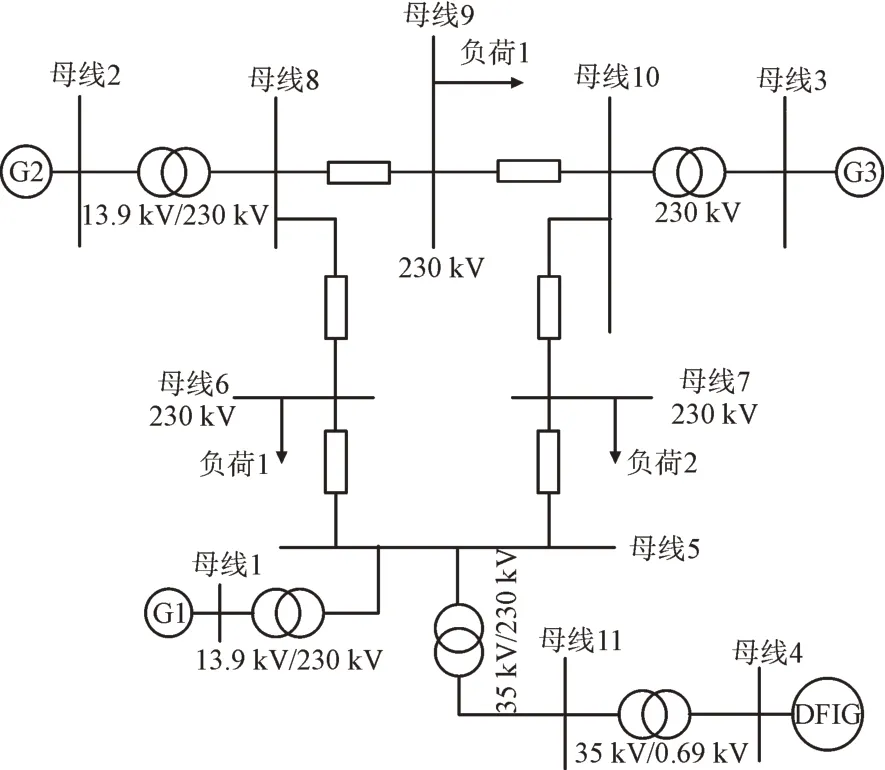
图10 算例系统图Fig.10 System simulation structure diagram

表1 同步发电机参数表Table 1 Parameters of synchronous generator

表2 双馈风机组参数表Table 2 Parameters of DFIG

4.1 惯量控制及对同步机抑制作用验证分析

风电场中机组运行风速均为Vwind=8 m/s，系统负荷为1 770 MW，当t=35 s 时，系统负荷增加200 MW，kp为锁相环比例控制参数，ki为锁相环积分控制参数，不同锁相环控制参数下系统频率响应、风电机组和同步机输出功率响应情况如图11、图12 所示。

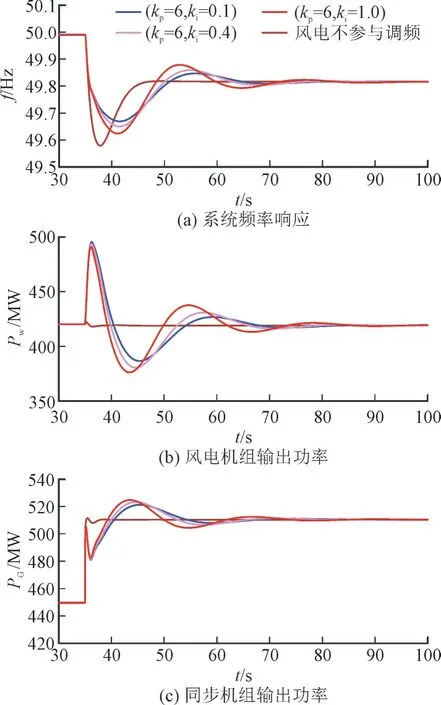
图11 变锁相环积分值下系统内各机组及频率响应Fig.11 System frequency response and output power response of wind turbine and synchronous motor with variable PLL integral value

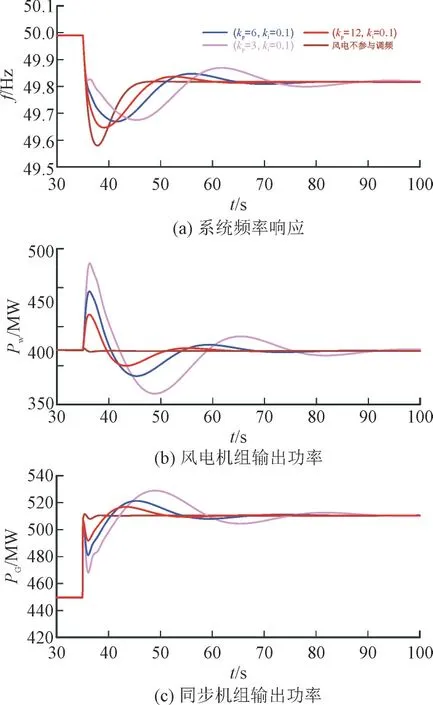
图12 变锁相环比例值下系统内各机组及频率响应Fig.12 System frequency response and output power response of wind turbine and synchronous motor with variable PLL proportional value

改变网侧锁相环的kp参数值，放慢风电机组网侧锁相环的锁相速度，可以较为明显地使DFIG 呈现出与同步发电机类似的惯量特性，kp参数越小，风电机组在系统中的惯量支撑作用也越为明显，同时也由图12 的（b）图与（c）图对比可知，风电机组对于系统惯量支撑程度越大，对同步发电机参与系统一次调频响应抑制效果越强。

4.2 协同控制策略作用验证分析

风电机组采用基于锁相环优化动态过程的惯量控制，并对同步发电机组1 附加风-火协同控制策略（Kc1=1.16，Kc2=Kc3=0），风电机组锁相环参数为kp=6，ki=0.1，t=35 s 时，系统增加200 MW 负荷时，系统响应情况如图13 所示。

由图13 可知，在36 s 时，风电场惯性响应增发出力由零增至最大值，此刻风电场约增发71 MW，仅采用风电惯量控制时，同步发电机1 该时刻受到由风电场出力的抑制作用增发出力仅约为31 MW。采用风-火协同策略后，风电场达到最大出力时增发67 MW，而此时该同步机增发出力约为59 MW，相较于仅采用风电惯量控制，风机达到最大出力时该同步机出力提升了约28 MW。

图13 风-火协同惯量控制策略对比验证图Fig.13 Comparison and verification of wind-thermal power cooperative inertia control strategy

仅采用风电惯量控制时，同步机组在46 s 达到最大出力522 MW，采用风-火协同惯量控制策略后同步发电机组调速器的响应速度加快，在约41 s 时达最大出力529 MW，一次调频过程中达到最大出力时间提前约5 s，最大出力提升7MW。

在对系统频率的优化效果方面，仅采用风电惯量控制时系统频率在41.3 s 达到最低点49.67 Hz，采用风-火协同控制调频策略后使得系统频率达到最低点时间延后至42.8 s，系统最低频率提升至49.72 Hz，相较于前者，系统频率达到最低点时间约延后1.5 s，系统最低频率提升了0.05 Hz，进一步改善了系统频率稳定性。

5 结论

本文验证了通过合理设置双馈式风力发电机组网侧锁相环参数，能够使风力发电机响应系统发生功率扰动时的频率变化，提供惯性支撑，该种控制方法无需对风机本身结构进行改造。

风电机组锁相环kp参数减小，风电在系统扰动作用下能提供的惯量支撑效果更明显，该种控制方法无需对风机结构进行改造，同时分析并验证了风电的快速惯量响应会暂时减少系统中的不平衡功率，进而抑制同步发电机一次调频的出力效果，进而设计了一种风电-火电协同调频控制策略，有效地减弱了系统层面风电场采用惯量控制对同步发电机一次调频的抑制作用，补偿了同步机组的一次调频信号，有效地提升了同步机组一次调频的调节速率，对系统频率暂态特性进行进一步优化，为未来风电机组参与系统频率调控提供优化策略。