数据驱动的风电机组传动系统疲劳载荷计算与主动抑制研究

张 斌，朱春生，贾鈜崴，姚 琦，马 博，谭志辉，罗智凌

（1.南方海上风电联合开发有限公司，广东珠海 519080；2.中国能源建设集团广东省电力设计研究院有限公司，广东广州 510663；3.暨南大学能源电力研究中心，广东珠海 519070；4.华北电力大学控制与计算机工程学院，北京 102206）

0 引言

近年来，风电装机容量迅速增加，风电场的运维已逐渐成为运营者关注的主要问题[1]。对于风电场而言，由于不存在燃料消耗成本，降低运维成本可明显提升其运行经济性[2]。其中，降低机组运行过程中的疲劳载荷可以有效地减少机组损伤，是降低运维成本的重要手段[3-5]。

风电机组作为多结构耦合而成的复杂机电系统，其运行过程中由于不确定的环境、运行工况等影响，不可避免地会产生损伤[6-7]。根据统计数据分析，在机组的机械结构中，传动系统是损坏比例最高、导致停机时间最长的结构之一[8]。因此，国内外研究人员在针对风电机组疲劳损伤抑制的研究中通常都将传动系统作为主要研究目标之一[8-9]。同时，考虑到机组疲劳损伤通常与机组运行工况相关，针对疲劳损伤的抑制研究通常与机组有功控制相结合[10]。

根据现有研究，传动系统疲劳损伤的表征参数包括主轴转矩的标准差和损伤等效载荷（Damage Equivalent Load，DEL）2 种。其中，主轴转矩的标准差是目前文献中针对传动系统疲劳载荷在线优化的主流参数[11-12]。然而，文献[13]指出，主轴转矩的标准差虽确实与传动系统疲劳相关，但并非完全线性相关。相比之下，DEL 利用雨流计数法[14]和Palmgren-Miner 准则[15]实现对机械结构损伤的描述，可以更准确地表征传动系统疲劳特性。但是由于DEL 计算方法复杂，现有研究一般难以其作为直接指导风电场实时优化运行的指标，只能作为后评估参数使用[11]。文献[16]中尝试使用机组的平均风速和平均功率作为工况参数去描述相应工况下的传动系统DEL 变化情况，并使用查表法完成基于工况的风电场内机组功率优化分配。然而，该研究的工况描述仅考虑平均风速和平均功率，场景设计过于简单，难以准确描述实际运行的复杂工况下传动系统DEL 的真实情况。

本文提出一种基于深度神经网络（Deep Neural Network，DNN）的传动系统DEL 数据驱动计算方法，使得DEL 参数可以直接用于风电场实时优化控制过程。仿真实验结果表明，基于数据驱动的DNN模型可以实现传动系统DEL 较为准确地计算和预测，同时直接针对传动系统DEL 的优化算法可在实现有功目标的基础上明显降低传动系统疲劳损伤。

1 传动系统疲劳载荷数据驱动建模

1.1 传动系统疲劳分析

在风电机组传动系统中，主轴将风轮转子的轮毂连接到齿轮箱或直接驱动发电机，研究中通常考虑主轴的柔性与阻尼特性，将传动系统用双质块模型进行表征[17]，数学表达式为：

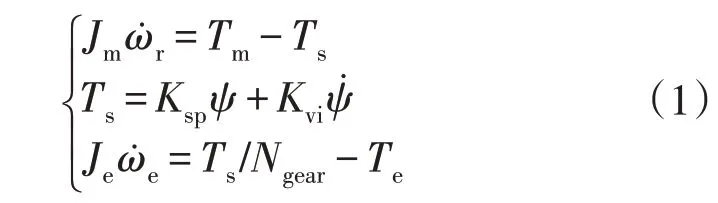
式中：ωr为转子速度；Jm为风轮转动惯量；Je为发电机转动惯量；Tm为机械转矩；Te为发电机转矩；Ts为主轴转矩；Ngear为齿轮箱的变速比；Ksp为主轴弹性系数；Kvi为主轴阻尼系数；ψ为扭转角度且=ωr-ωe/Ngear。

双质块模型及对应各参数如图1 所示。

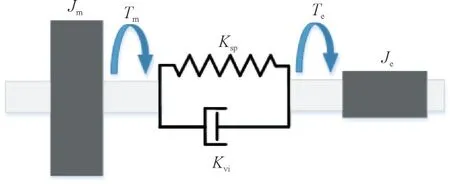
图1 风电机组传动系统双质块模型Fig.1 Two-mass model of wind turbine transmission system

根据式（1）所示模型，风速的随机波动可导致风轮转子侧转矩产生波动，另一侧的电磁转矩则由于发电任务需要保证与所需的功率适配，这样的结构导致了不平衡转矩的存在。动态不平衡会使轴系出现振动并引起损伤，因此一般认为主轴转矩的波动情况可以用来表征传动系统疲劳载荷。另外，风机传动系统通常还包括齿轮箱和连接到发电机的高速轴，但由于比主轴短很多，高速轴可简化为刚性结构，齿轮箱疲劳则一般也采用主轴载荷作为度量[18]。

1.2 传动系统DEL计算方法

在工程应用中，损伤等效载荷DEL 被广泛认可为典型的风机疲劳度量参数。使用雨流计数法将复杂的载荷历史转换为影响疲劳的载荷反转集合，然后采用Palmgren-Miner 法计算得到DEL。使用疲劳寿命曲线（式2）和Palmgren-Miner 规则（式3）：

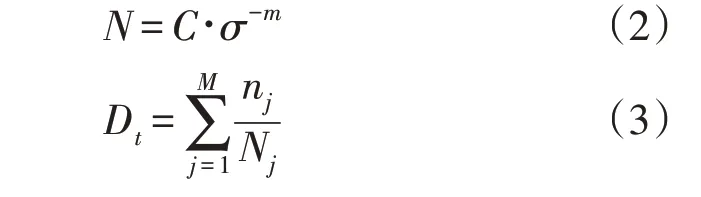
式中：σ为应力幅度；N为材料可以承受的幅度σ的循环数；C为材料可以承受的最大静态应力；m为Wöhler 系数参数；M为应力分区数量；nj为结构在应力水平σj下经历的循环次数；Nj为应力幅度σj导致部件失效的循环次数。

DEL 的物理意义为恒定频率f下产生与时间T中的原始信号相同的损伤的正弦应力的振幅，其值FDEL为[19]：

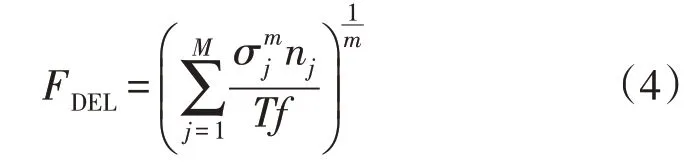
出于控制效果比较的目的，DEL 的相对值很重要，因此通常使用Tf=1。同时，用于计算传动系统的DEL 的Wöhler 系数m取值为4。

根据式（2）—式（4）可以看出，DEL 的计算严重依赖于转矩等机组运行工况数据的长期准确测量，并且所用雨流计数的计算过程复杂，这些条件导致DEL 指标难以适用于风电机组的在线优化控制过程，目前的研究仅将其作为后评估策略。

1.3 数据驱动的DEL计算实验设计

考虑到DEL 指标的理论计算复杂度，本文考虑设计一种基于数据驱动的DEL 计算方法。为保证算法可实现性，首先对用来描述DEL 的机组特性参数进行选取。结合DEL 理论计算方法和式（1）所示传动系统机理模型，可以看出主轴转矩的波动与机械侧和电气侧的波动情况均相关，而两侧的波动主要来源于风资源的波动和有功出力的波动。本文选取机组运行工况参数中的平均风速vˉ、湍流强度I、平均功率Pˉe、功率标准差Std（Pe）以及功率变化量的标准差Std（ΔPe）5 个参数作为描述传动系统DEL 的基础参数。这5 个参数在实际应用中均可以通过SCADA 系统中的数据经过简单计算得到，数据获取难度远小于转矩等参数。

式中：Ns为计算周期内的采样点数；vi为第i个计算周期内的采样风速。

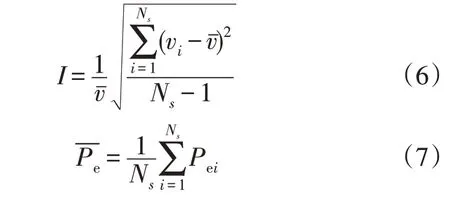
式中：Pei为第i个计算周期内的采样有功功率。

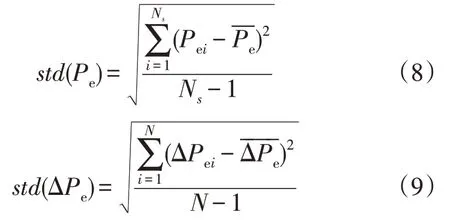
式中：ΔPei为相邻采样有功功率的变化量。

本文后续计算中，计算周期为5 min，采样周期为1 s。

基于式（5）—式（9）所选参数，本文依据蒙特卡洛实验法[20]选取参数均匀分布的多种工况，测试不同工况下风电机组传动系统DEL 情况。

1.4 基于DNN的传动系统DEL数据建模

为了进一步对传动系统DEL 进行更准确的描述，采用深度神经网络对1.3 节蒙特卡洛实验结果进行训练和学习。

1.4.1 DNN网络构建

DNN 的内部网络结构一般包含输入层，隐含层以及输出层3 类。第一层是输入层，最后一层是输出层，中间的都是隐含层，本文所建DNN 网络具有两层隐含层，层与层之间通过神经元互相连接，具体结构如图2 所示。

图2 DNN结构示意图Fig.2 Schematic diagram of DNN structure

1.4.2 DNN的传播与优化

1）前向传播

DNN 在运算过程中利用了多层神经元之间不同的权重系数ω和偏置向量b，实现从输入层到输出层的运算，计算公式如下：

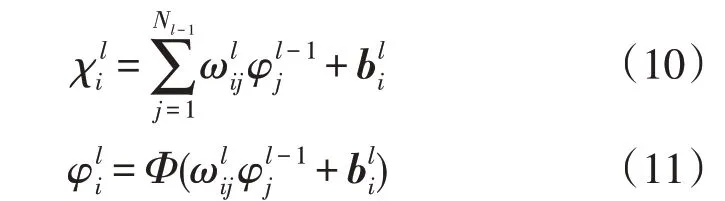
式中：为l层i神经元的输入量；为l层i神经元的输出量；Nl-1为l-1 层的元个数；为l层i和j神经元之间的权重系数为l层i神经元的偏置向量；Φ为激活函数（本文仿真中选择Sigmoid 函数）。

2）反向传播

反向传播的目的是通过合理的损失函数迭代优化完成正向传播中权重系数ω和偏置向量b的更新。本文将损失函数J定义如下：

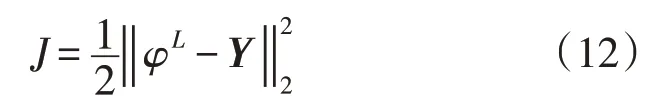
式中：Y为输出变量的真实值向量；为二范数计算。

为了完成权重系数ω和偏置向量b的更新，进行如下计算：

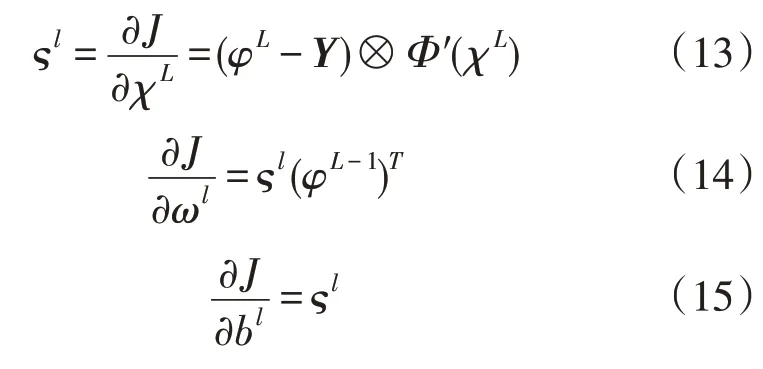
式中：ςl为l层的损失函数关于输入的偏导，也可称为灵敏误差；Φ′为激活函数的导函数。

通过式（14）—式（15）可实现权重系数ω和偏置向量b的更新。然而，在DNN 网络的训练中，随着网络深度的增加，参数可能会在更新过程中偏离其设定范围。为应对这一问题，本文采用Adam 算法在训练的同时计算梯度的指数加权平均数，再利用得到的梯度值来更新参数。限于篇幅此处不再详述，相关算法可见于文献[21]。

2 数据驱动的风电场有功调度算法

基于第1 节学习得到的风电机组传动系统疲劳载荷数据驱动计算模型，可实现利用风电场数据采集与监视控制（Supervisory Control And Data Acquisition，SCADA）系统中易得的数据而预测出传动系统DEL的实时数值。因此，快速计算得到的传动系统疲劳载荷情况可以用于风电场有功调度的实时功率优化分配，利用有功功率的优化分配实现风电场内机组传动系统疲劳载荷的有效抑制。

2.1 优化目标设置

本文所提优化算法旨在风电场运行于有功控制模式（限功率、参与系统调峰调频等工况）下，降低风电场内机组传动系统的疲劳载荷。因此，算法在降低机组传动系统DEL 的基础上，需要首先保证风电场功率需求和风电机组的功率上下限约束。优化问题和约束条件可以描述为：

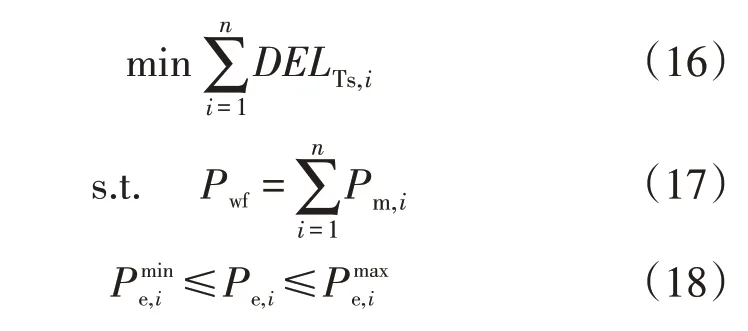
式中：n为风电场机组数量；Pwf为风电场整体出力；Pe，i风电场中第i台风机的有功出力；和分别为实际风速下的最小和最大出力；DELTs,i为风电场中第i台机组传动系统的疲劳载荷。

2.2 优化方法选取

2.1 节中所描述的优化问题已有较为成熟的求解算法和多种商业求解软件。然而，由图3 可知传动系统DEL 与功率的标准差有明显的正相关趋势，这意味着功率值保持不变时传动系统DEL 较低，功率指令值与疲劳载荷的关系可近似为1 个以上一时刻功率值为低点的凸函数。因此本文选用MATLAB 中自带的凸优化求解器进行优化求解。图3 为任选了5 个工况下机组指令值与数据驱动模型计算的传动系统DEL（图5 中纵坐标DELTs）的关系曲线，验证了上述猜想。

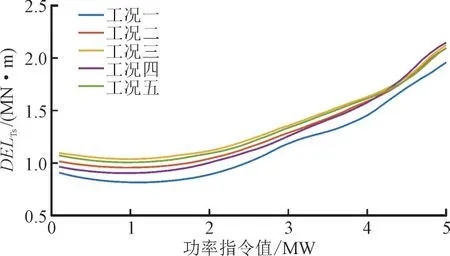
图3 风电机组在不同功率下的DEL值Fig.3 DEL value of wind turbines at different power levels

3 算例分析

3.1 仿真实验设置

通过SimWindFarm 平台搭建风电场仿真系统。在数据驱动建模阶段，基于SimWindFarm 平台[22]设计蒙特卡洛实验，选取NREL 5MW 机型[23]进行仿真实验。为了保证统计结果的准确性，风电机组参数及实验工况设置如表1 和表2 所示。

表1 NREL 5 MW风电机组参数Table 1 NREL 5 MW wind turbine parameters

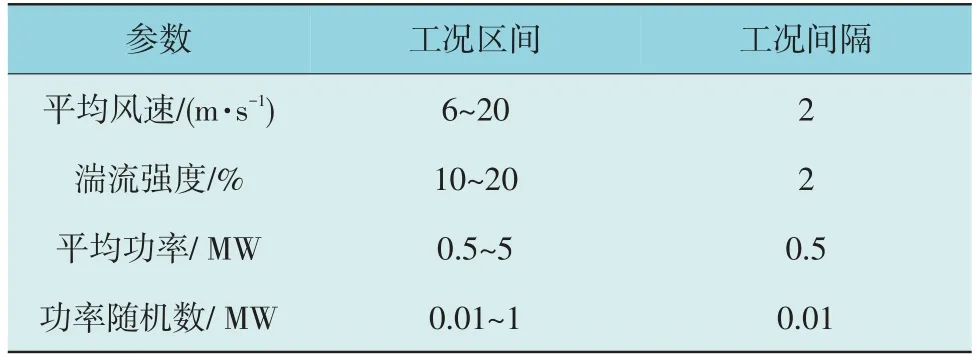
表2 风电机组实验工况设置Table 2 Setting of experimental conditions of wind turbines

在有功调度验证阶段，仿真风电场包含5 台NREL 5 MW 的风电机组模型，以5×1 的形式排列，风机之间间隔距离为700 m，如图4 所示。图4 及后续图表中使用“WT1”表示1 号风电机组，并以此类推。仿真中各风电机组受到尾流效应影响，具体风速波动情况如图5 所示。同时，本文采用了工程中常用的等比例分配算法[24]作为对照，而改进算法则采用了第1 节中DNN 网络学习得到的疲劳载荷模型作为优化的基础。

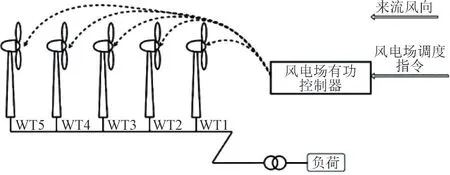
图4 仿真系统结构图Fig.4 Structure diagram of simulation system

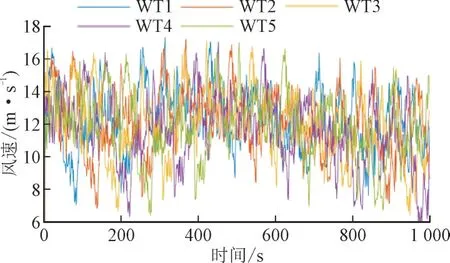
图5 仿真风速Fig.5 Wind speed in simulation

3.2 数据驱动DEL建模结果

表2 中，机组运行过程中的平均风速、湍流强度、平均功率可以经由SimWindFarm 平台直接预设，共480 组工况，参数等间隔均匀设置。功率标准差及功率波动的标准差无法直接预设，本文选择在仿真中在机组功率设定值上添加范围可变的随机数，共100 组随机数。因此，本文通过SimWindFarm平台构造出48 000 中不同工况进行实验。

通过SimWindFarm 工具箱仿真，在计算出风机的平均风速、湍流强度、平均功率、功率标准差和功率波动的标准差之后，再使用MCrunch 代码[25-26]完成DEL 的计算。图6 以平均风速、湍流强度、平均功率、功率的标准差、功率波动的标准差为X轴，传动系统DEL 值为Y轴画出了48 000 组实验结果图。

由图6 中结果可知，传动系统DEL 与功率标准差及功率波动的标准差有明显较强的相关性，与平均风速、湍流强度、平均功率相关性较弱。这一结果表明，以往研究中将传动系统DEL 仅由平均风速、平均功率2 个工况进行描述的方法具有明显的局限性，功率的波动情况对传动系统DEL 的影响更为明显。

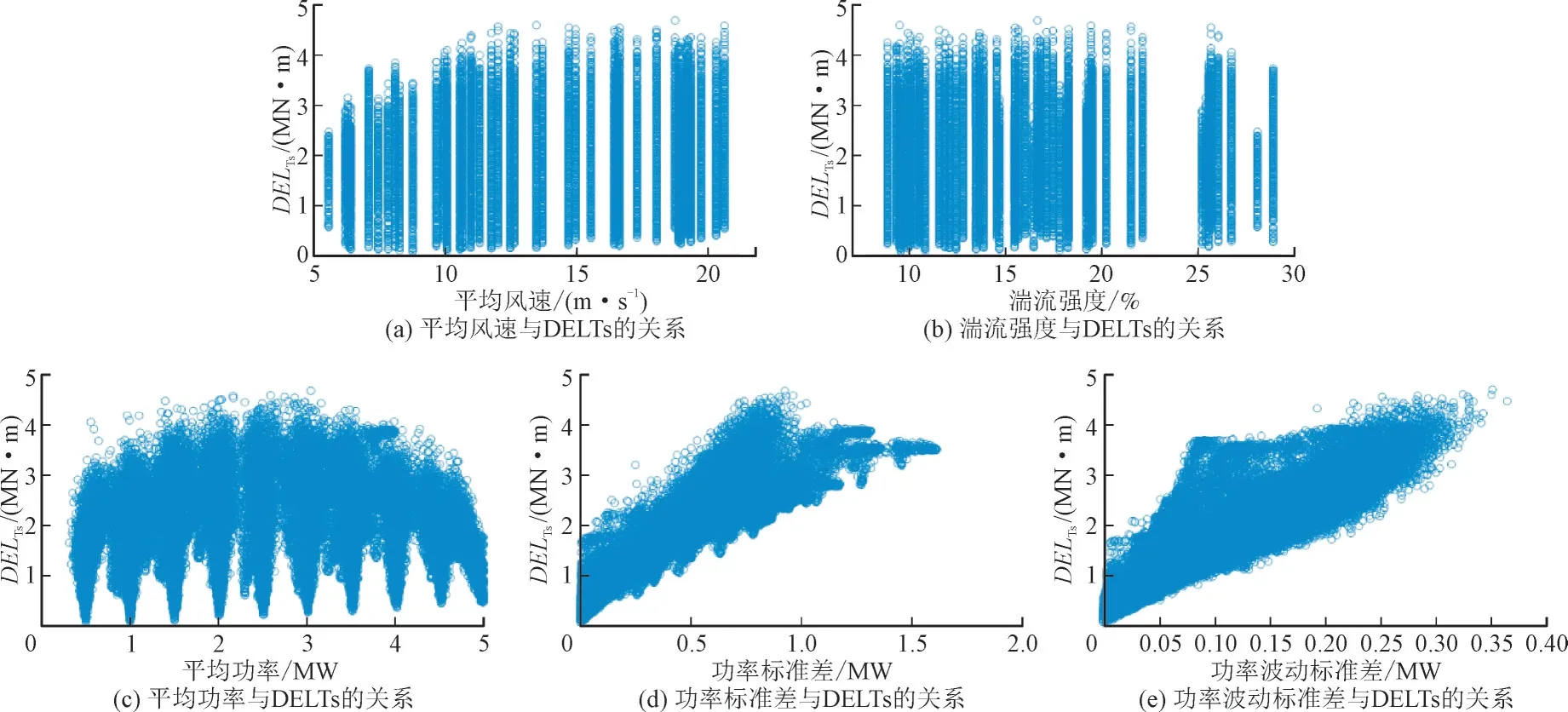
图6 48 000组工况计算结果Fig.6 Calculation results of 48 000 sets

采用1.4 节中的DNN 算法训练出的DNN 网络，将48 000 组不同工况下的输入与输出分成了前45 000 组和后3 000 组。其中，前45 000 组数据设置为训练集，后3 000 组数据设置为测试集。在模型训练成功之后，采用均方根误差（Root Mean Squared Error，RMSE）来评价模型的性能，RMSE 的值用ERMS表示，并且将预测值和真实值进行了对比，均方根误差已经接近0，预测结果与实际结果的平均绝对值误差为13.67%，预测数据可以较好地拟合原始数据，如图7 所示。

由图7 可知，根据DNN 网络学习得到数据模型，可实现利用风速、功率等易获得的简单数据对传动系统疲劳载荷的较为准确的估计。

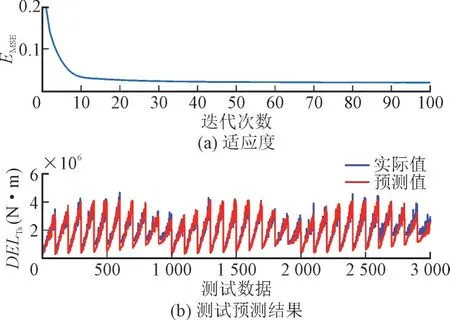
图7 神经网络性能评价Fig.7 Performance evaluation of neural network

3.3 有功控制仿真结果

在本算例中，为了验证本文风电场有功控制算法可以满足恒功率跟踪和爬坡跟踪的要求，对风电场的有功调度指令设置如下：前400 s 为5 MW，400～700 s 内从5 MW 爬坡至10 MW，700 s 后保持10 MW 不变。在功率控制算法上，对照组从0～1 000 s 均为比例分配算法，实验组在0～400 s 为比例分配算法，400～1 000 s 为优化控制算法。仿真实验结果图8—图10 所示。

图8 风电场有功控制效果对比Fig.8 Comparison of active power control between wind farms

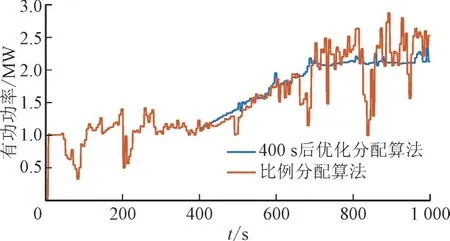
图9 WT1风机有功出力对比Fig.9 Comparison of active power output of WT1

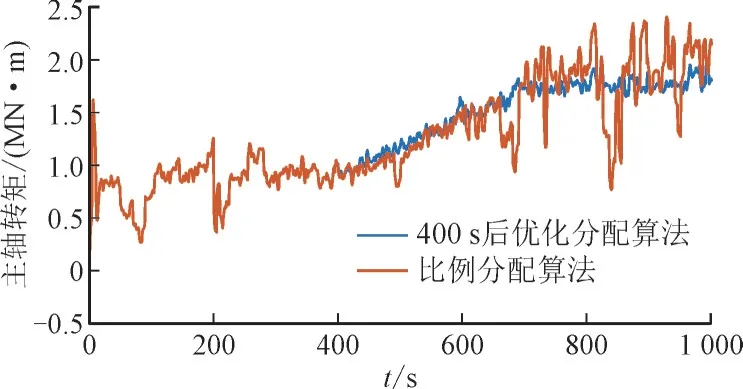
图10 WT1风机主轴转矩对比Fig.10 Comparison of main shaft torque of WT1

图8 展示了基于本文所提的优化有功控制方案和比例分配方案在风电场层面的效果。可以看出，2 种方案均能保证风电场出力对功率指令值较好的跟踪。另一方面，虽然场级功率跟踪效果相似，2 种策略对机组的功率分配结果则差异明显。图9 选取了WT1 风机作为示例，在2 组实验中，前400 s 的功率控制方法相同，有功出力情况也相同，400 s 之后采用优化分配算法的实验组风机有功出力明显更为平滑，这一结果也符合前文中关于功率波动与传动系统疲劳载荷情况的分析。图10 展示了WT1 风机的主轴转矩波动情况，实验组的优化控制算法同样对主轴转矩的波动情况产生了较好的平抑作用。

进一步地，采用MCrunch 对实验组和对照组的传动系统DEL 进行理论计算，计算结果如表3 所示。

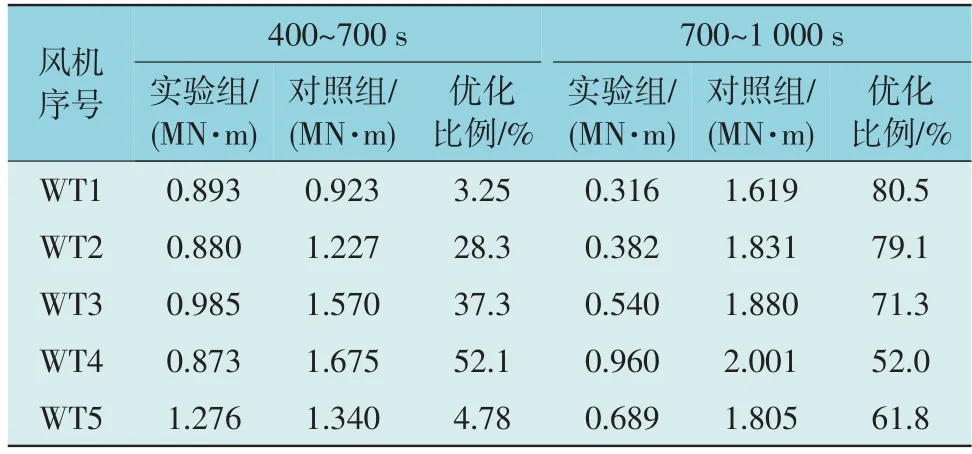
表3 传动系统DEL对比Table 3 DEL comparison of transmission system

表3 结果显示，在整个有功调度过程中，每台机组的传动系统DEL 值有所下降。值得注意的是，在700～1 000 s 之间，由于风电场处于恒功率跟踪状态，采用优化算法带来的传动系统DEL 值降低幅度更为明显，可见较为平稳的有功功率输出对机组传动系统的损伤抑制有着重要作用。而在400～700 s之间，风电场处于功率爬坡状态，场内机组的功率也均在爬升，在这段时间内本文优化控制策略对应的机组传动系统DEL 在部分机组上的优化程度较低（如WT1 和WT5），但总体上相对于传统分配算法也取得了更好的传动系统载荷平抑效果。

4 结论

本文着力于构建风电机组传动系统DEL 的数据驱动计算模型，并将其应用于功率—疲劳的联合优化控制中。设计了仿真风电机组的48 000 种不同工况，通过平均风速、湍流强度、平均功率、功率的标准差、功率波动的标准差5 组参数作为输入，设计DNN 并进行训练，得到了预测准确度高于87%的传动系统DEL 模型。基于该模型进行传动系统DEL 值的实时在线预测，可在对风电场有功功率实时控制的过程中实现风电场内所有机组的传动系统疲劳载荷抑制。本文得出的神经网络对风电场传动系统DEL 值的预测具有良好的适用性，基于此的优化调度方法也显示出明显的优势，本文所研内容可为提高风电场灵活经济运行奠定良好基础。