含换流器型电源电力系统的短路计算方法

翁 华，朱维骏，张 旭，郁 丹，杨亚楠，李宇骏，唐 人

（1.浙江华云电力工程设计咨询有限公司，浙江杭州 310006；2.西安交通大学电气工程学院，陕西西安 710049）

0 引言

随着可再生能源的大规模应用以及换流器技术的快速发展，换流器型电源（Converter Interfaced Generations，CIGs）逐渐成为当代电力系统的主流发电形式之一。相较于传统的同步发电机，经电压源型换流器（Voltage Sourced Converter，VSC）馈入的新能源发电技术能够实现有功功率和无功功率的快速解耦控制，并为系统的稳定运行提供重要支撑[1-4]。同时，新能源发电机组的短路特性受控制作用影响，较传统同步发电机有明显区别。随着大量换流器型电源的接入，交流系统短路电流特性发生较大变化。因此，详细分析换流器型电源对交流系统短路电流的影响程度和贡献水平是十分必要的。

国内外学者对含电力电子换流器电力系统的短路电流特性，以及换流器对短路电流的影响机理进行了大量的研究[5-24]。文献[5-9]分析了风场及光伏电站对电网短路电流特性的影响并给出了对应的短路电流计算方法。文献[10-12]研究了基于PQ 控制策略的逆变型分布式电源（Inverter Interfaced Distributed Generation，IIDG）在系统故障时所提供的短路电流特性和故障等值模型。文献[13]分析了采用不同类型控制器的逆变器型分布式电源对系统短路电流的影响。文献[14-15]分析了含低电压穿越型分布式电源配电网的短路电流特性及短路电流计算方法。文献[16-20]分别研究了现有几种高压直流输电系统逆变侧的短路电流特性，并给出短路电流的解析表达式。文献[21-24]分析了在不对称故障下含逆变型分布式电源电力系统序电流的动态特性，并给出了相应的短路电流表达式。文献[25]则重点分析了柔性直流对交流系统短路电流的影响。但鲜有文章考虑在系统故障暂态过程中，换流器控制模式切换对系统短路电流水平的影响。

因此，本文主要研究考虑换流器控制模式切换下电力系统短路计算方法。首先建立换流器型电源的控制模型，并给出电网故障下换流器可能进入的控制模式。其次，给出考虑控制模式切换的含CIG 电力系统的稳态短路电流计算方法。最后，通过数值计算和电磁暂态仿真验证了所提计算方法的准确性。

1 换流器型电源的控制模式

对于并网运行的换流器型电源，一般采用经典的PQ 控制策略控制其注入交流主网的功率[26]。换流器型电源的等值电路图和常用PQ 控制器的控制结构图分别如图1 和图2 所示。整个控制系统将在dq坐标系，即同步参考坐标系中实现。

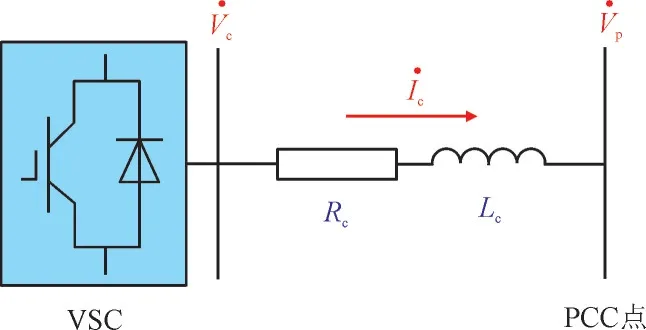
图1 换流器型电源等值电路Fig.1 Equivalent circuit for CIG

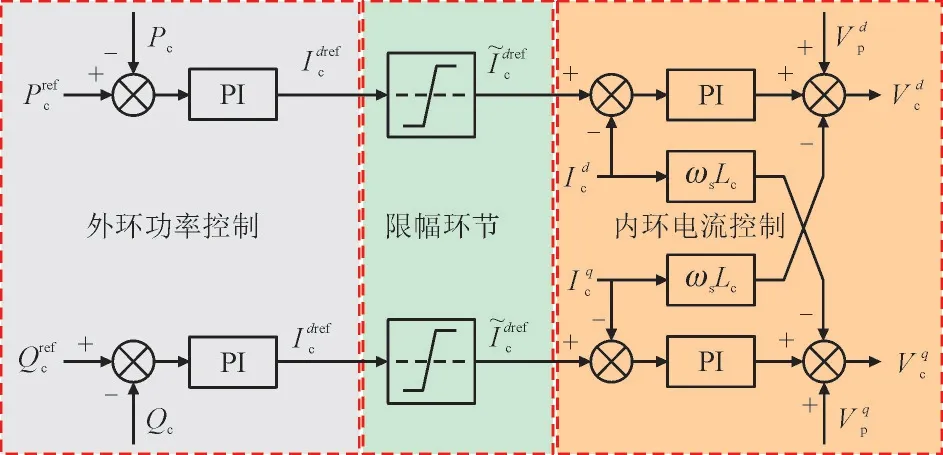
图2 典型PQ控制器传递函数框图Fig.2 Block diagram of classical PQ controller

图1 中和分别为换流器端口电压及系统公共连接点（Point of Common Coupling，PCC）点电压；Ic为换流器型电源输出电流相量；Rc和Lc分别为输电线路的等值电阻和等值电感。图2 中Pc和Qc分别为换流器型电源实际输出的有功功率和无功功率；上标ref 为该电气量的参考值；上标d和q则分别为该电气量的d轴分量以及q轴分量；～为受幅值限制后的电气量；ws为交流系统额定角频率；PI表示比例-积分控制环节。

为了能够最大程度地利用换流器的有功功率传输能力，在电力系统正常的条件下，常令换流器工作在单位功率因数控制模式。此时，换流器输出电流的q轴分量将被调制为零，即换流器输出电流相量与PCC 点电压相量间的夹角为零[27]。换流器型电源输出功率的具体表达如下：

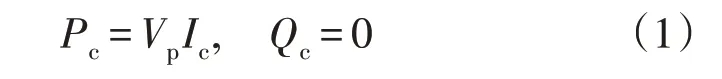
在常见的PQ 控制器中，外环功率控制环节主要起到调节经换流器注入到交流主网的有功功率和无功功率的作用。故CIG 的外环功率控制方程可写成如下形式：

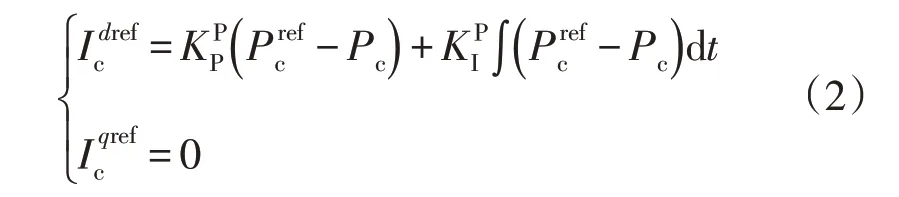
近年来，电力系统运行准则普遍要求换流器型电源在交流主网发生故障时能够发出一定量的无功功率以提高换流器本身的低电压穿越（Low Voltage Ride Through，LVRT）能力，故需要在换流器控制环节配置低电压穿越控制器来调制换流器输出电流的q轴分量。因此，在考虑低电压穿越控制策略后，换流器输出的q轴电流参考值需要满足以下方程：

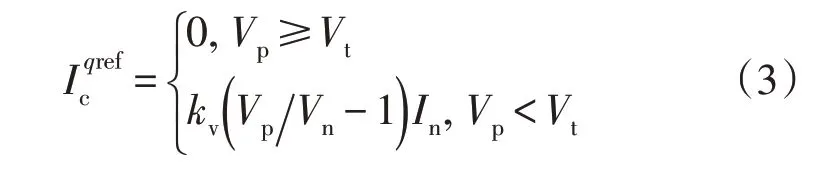
式中：Vt为激活并网换流器提供无功功率支撑的阈值电压；kv为无功功率支撑系数；Vn和In分别为PCC点的额定电压和换流器注入电流的额定值。

为了确保系统发生故障时，换流器型电源不会因过流而损坏，通常需要在外环功率控制环节的输出端口设置一个电流限幅器以抑制换流器输出的短路电流幅值。经过电流限幅器作用后，换流器输出电流的具体表达如下：

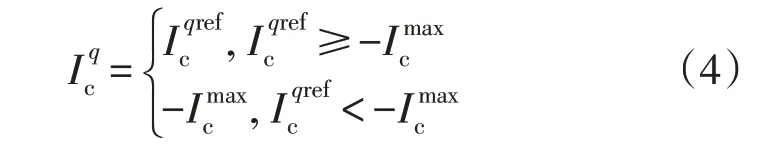
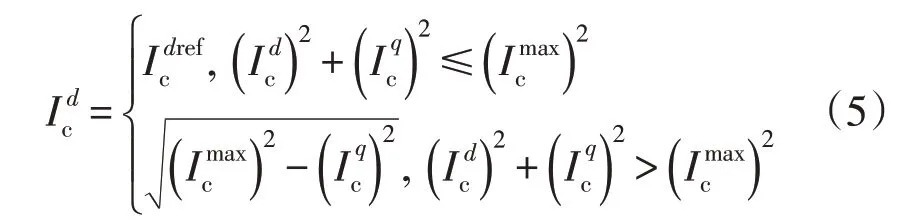
基于式（4）和式（5）可以得出结论：带有低电压故障穿越能力的并网换流器可在电力系统故障期间切换为以下4 种控制模式之一。

模式一：PCC 点电压略有下降，换流器不会发出无功功率。通常情况下，当PCC 点电压波动较小时，换流器型电源可以按照参考值传输有功功率。此时，以下约束条件成立：

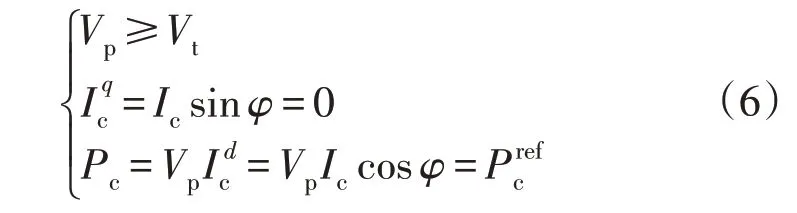
式中：φ为由低电压穿越控制策略提供的电流相角。

模式二：当PCC 点电压跌落一定范围后，并网换流器可以在不触发电流限幅器的前提下为电力系统提供无功支撑。此时，换流器型电源需要满足以下约束条件：

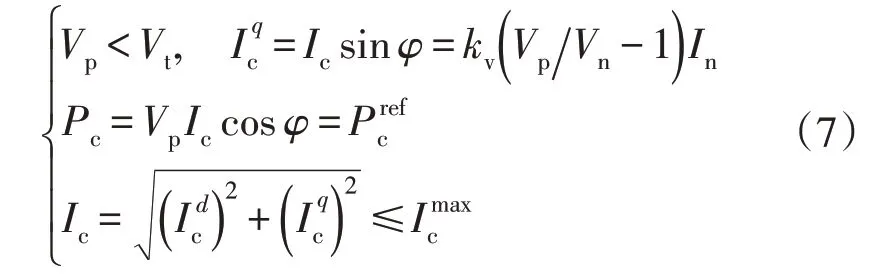
模式三：当PCC 点电压跌落比较大时，使得换流器q轴电流能够跟随其参考值，而换流器d轴电流由于电流限幅器的作用而小于参考值。此时，换流器型电源所需要满足的约束条件如下：

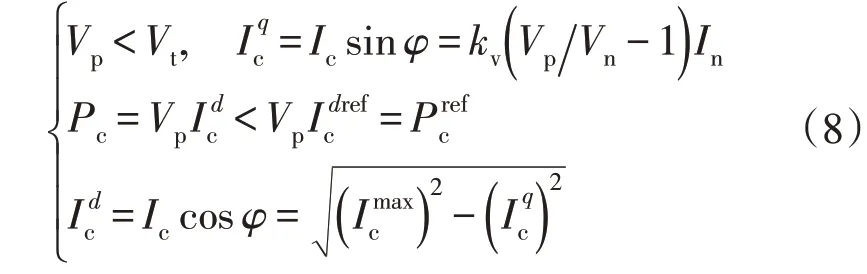
模式四：当PCC 点电压急剧下降时，并网换流器仅能以其最大输出电流为系统提供无功功率支撑。当换流器处于模式三与模式四的切换点时，可导出PCC 点临界电压的数学表达：

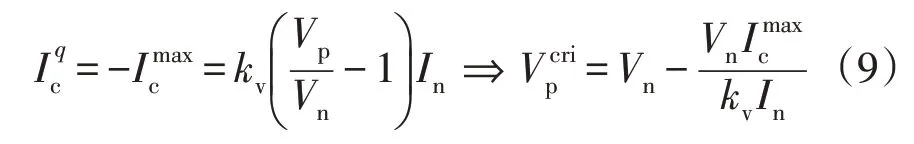
此时，模式四下换流器型电源需要满足以下约束条件：

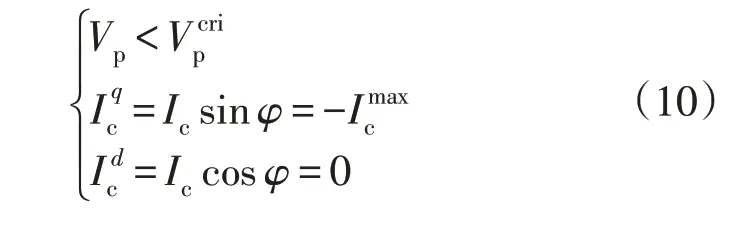
综上所述，换流器型电源在不同控制模式下所需要满足的约束条件如表1 所示。

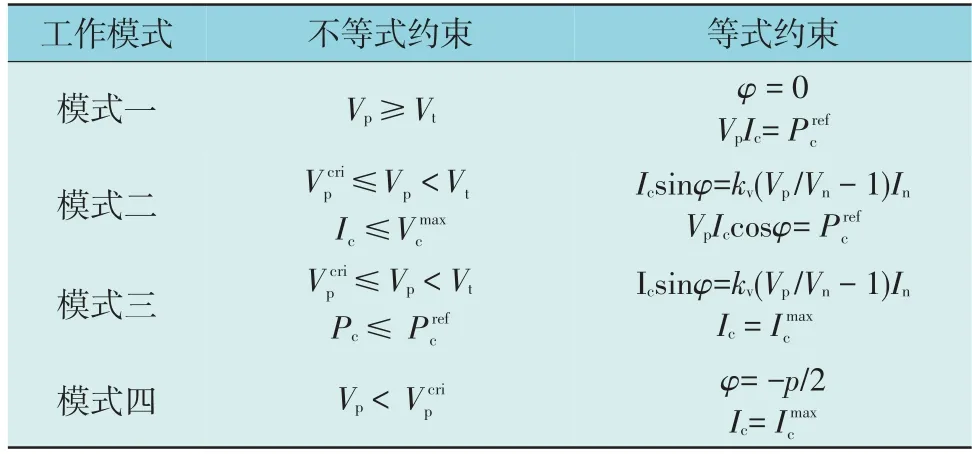
表1 不同控制模式下的换流器型电源约束Table 1 Constraints of CIG with different control modes

针对表1 中处于不同控制模式下的换流器型电源，建立含CIG 电力系统的故障网络模型，分析其短路电流特性，并给出适用于该类型电力系统的实用短路电流算法。

2 含CIG电力系统短路电流计算方法

2.1 同步发电机的故障分析模型

在实用短路电流计算中，同步发电机可以等效为一个与次暂态电抗并联的恒定交流电压源。其动态方程可描述为：

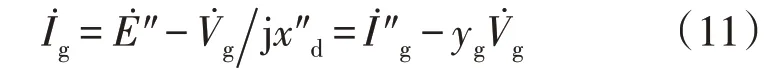
式中：为同步发电机的次暂态电动势；为同步发电机的次暂态电流；为同步发电机的次暂态电抗；yg为同步发电机的等效电纳；Vg和Ig分别为同步发电机端口的输出电压和输出电流。

式（11）采用了同步发电机的诺顿等效模型，以便推导出含CIG 电力系统的短路电流计算方法。

2.2 含CIG电力系统的网络模型

本文所研究的含CIG 电力系统的等效网络结构如图3 所示。

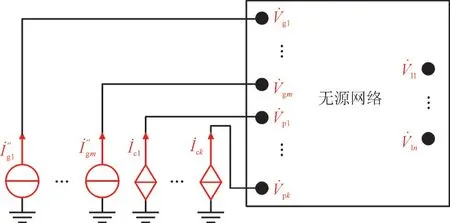
图3 含CIGs的电力系统的等效网络Fig.3 Equivalent network of power system with CIGs

为了简化短路电流的计算及分析过程，本文所研究的含CIG 电力系统中的负荷节点均采用恒定阻抗模型，而各负荷节点的等效阻抗均可通过故障前电力系统的稳态潮流计算求得。基于以上条件，可以得到故障发生时，所研究电力系统的网络方程。其中，下标m，n，k分别为同步发电机节点、换流器型电源节点以及负荷节点的个数。因此，对于如图3 所示的含CIGs 的电力系统，其故障网络方程可以写成以下形式

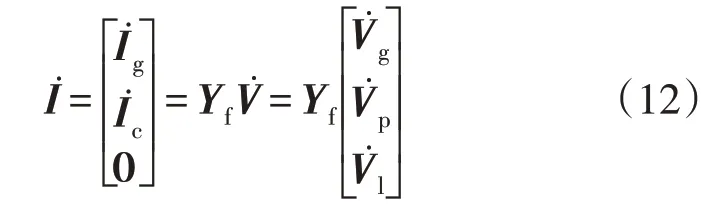
式中：Ig和Ic分别为同步电机节点电流列向量以及换流器节点电流列向量；Vg，Vp和Vl分别为同步电机节点电压列向量、PCC 点电压列向量以及负荷节点电压列向量；Yf为所研究系统的故障导纳矩阵。

将式（11）与式（12）联立，即可得到以下网络方程：

式中：Yij为与每一个电压列向量对应的分块导纳阵。

Yij具体定义如下：

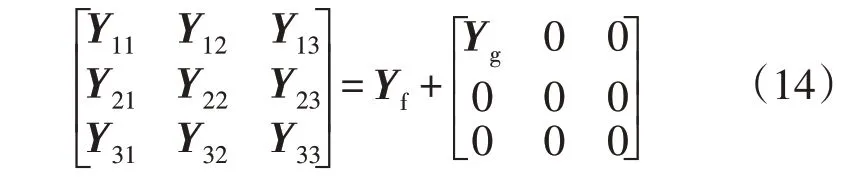
式中：Yg为与同步发电机节点对应的导纳矩阵。

基于式（13）和式（14），所研究系统的网络方程可以被简化为以下形式：

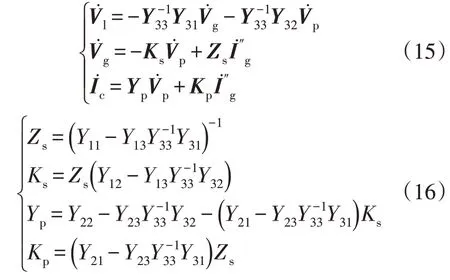
式中：Zs为同步阻抗；Ks为同步系数；Yp为换流导纳；Kp为换流系数。

基于式（15）和式（16），可快速求解含CIG 电力系统的故障潮流。

2.3 故障潮流的求解算法

由于低电压故障穿越控制作用，换流器型电源的输出电流相量在交流主系统故障期间可能与并网换流器PCC 点的电压相量不共线。故式（15）中换流器型电源的输出电流可写为以下的相量方程：

式中：θc为并网换流器PCC 点电压相量的相角列向量；φ为因为交流主系统提供无功功率支撑而额外产生的相角列向量。

换流器输出电流列向量以及PCC 点电压列向量的具体定义如下：

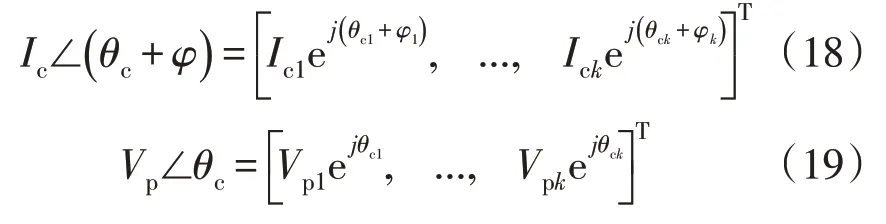
将网络方程（17）与式（6）—式（10）所描述的换流器型电源约束条件联立，可以得到如下系统方程：

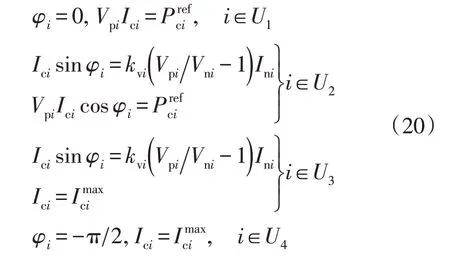
式中：下标i为系统中的第i台换流器型电源；U1—U4分别为处于不同控制模式下的换流器型电源集合。

联立式（18）—式（20），即可求得换流器型电源在系统故障时的短路电流。然而，对于某一特定故障，每一个换流器型电源的控制模式是不确定的，使得集合U1至U4中包含的元素无法直接确定。因此，本文通过交替迭代确定换流器控制模式及求解故障网络，所提算法流程图如图4 所示。

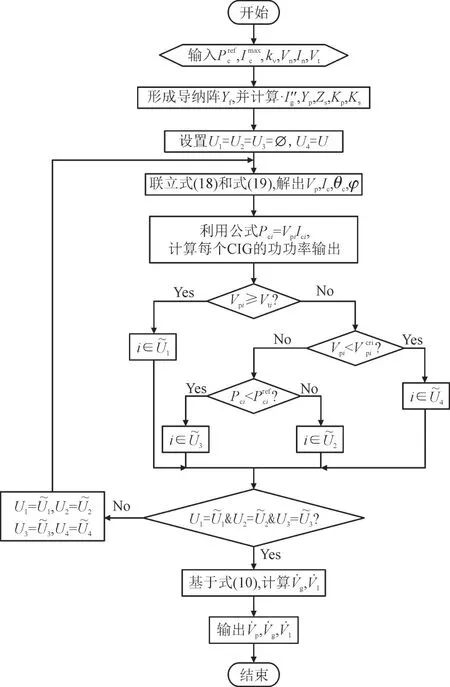
图4 用于故障分析的交替迭代算法Fig.4 Alternating iteration algorithm for fault analysis

在所提算法中，首先假设系统中所有并网换流器在电网故障后均切换至限流模式。因此，在设置初始集合时，仅将U4设置为全集，其余均设置为空集。每台换流器型电源的实际控制模式将通过以下迭代计算确定。

在估算环节中，通过联立式（15）和式（16）来估算换流器型电源的输出电流及PCC 点电压。其中，被估算的未知数总量为4k个，即k台换流器型电源的Vp，Ic，θc及j。网络方程包含k个复方程，而换流器型电源方程包含2k个实方程。故方程的数量等于未知数的数量。

在判别步骤中，PCC 点的估算电压可用于模式一和模式四的判别，而估算的换流器输出有功功率则用于区分模式二和模式三。所有换流器的控制模式都将存储在由U1—U4表示的集合中。最后，通过交替进行估算步骤和判别步骤，即可解决含CIG的电力系统的故障网络的潮流计算。

3 仿真分析

为了验证所提的含CIG 电力系统故障分析方法的有效性，在PSCAD/EMTDC 平台中搭建了IEEE 33 节点标准测试系统的详细模型，系统的具体拓扑结构如图5 所示。

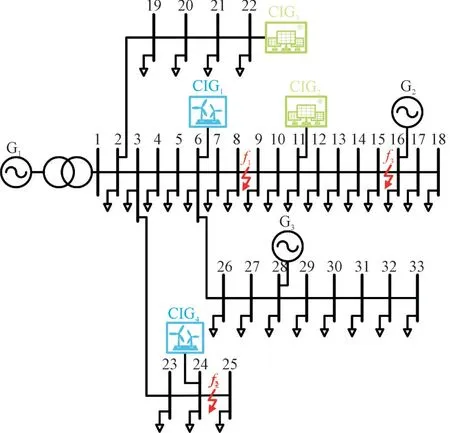
图5 含换流器型电源的33节点测试系统拓扑Fig.5 Typology of 33-bus test system with CIG

在该测试系统中，总共有4 台换流器型发电机，包含2 台光伏发电机（节点11、节点22）和2 台风力发电机（节点6、节点24）。此外，在节点16 和节点26 处还安装了2 台分布式同步发电机。每台分布式发电机的输出功率的参考值以及测试系统的其他主要参数列于表2。

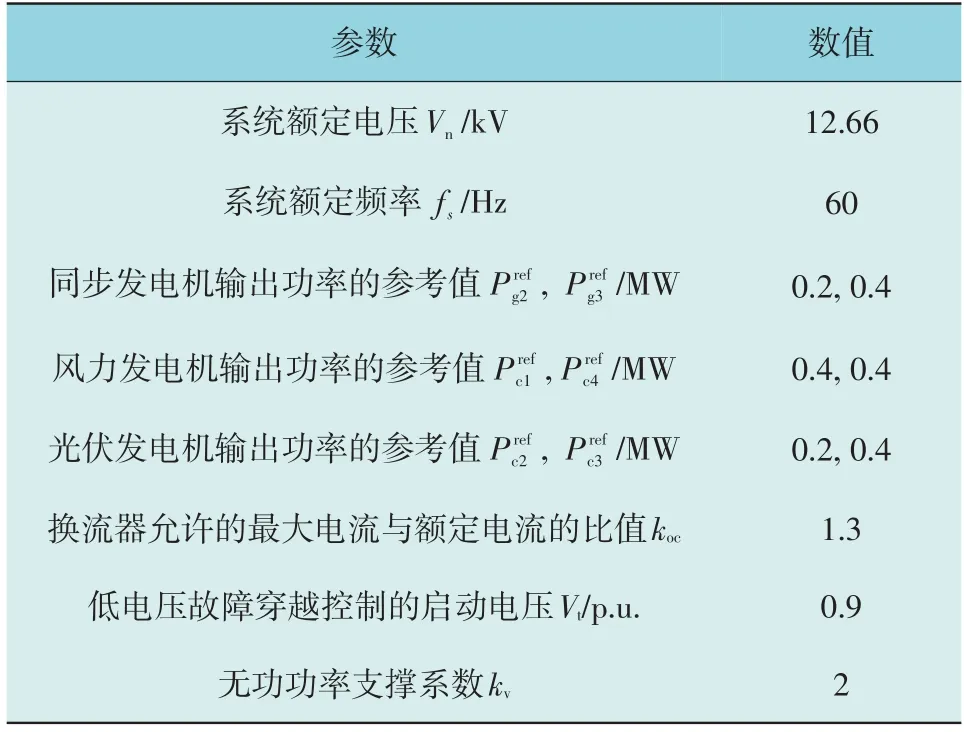
表2 33节点测试系统的主要参数Table 2 Main parameters of 33-bus test system

3.1 含CIG电力系统的故障特性

图6 展示了当节点8 和9 间的线路上靠近节点8 的位置发生金属性三相短路故障（d=0.2，rf=0.01 Ω，即图6 中f1所在位置）时，含CIGs 电力系统的动态响应过程。从图7（a）的波形中不难看出：当系统发生故障后，CIG2的输出电流很快上升至其极限值，且同时存在明显的相角偏移。这意味着在故障持续期间，由于LVRT 控制器的存在，换流器型电源CIG2试图产生更多的无功功率而导致自身输出电流的相角滞后。图6（b）则展示了各换流器型电源PCC 点电压的动态响应过程。其中，CIG3的PCC点电压超过启动LVRT 控制器设定的电压阈值11.394 kV，故其运行在控制模式1 状态。同时，CIG2的PCC 点电压却低于由式（9）确定的临界PCC点电压4.431 kV。由式（10）可知，此时CIG2运行在控制模式4 状态，并以最大输出电流向系统注入无功功率。至于其余的换流器型电源，它们的PCC 点电压均位于阈值电压和临界电压之间，故它们在故障期间同时产生有功功率和无功功率。从图6（c）中可以看出，CIG3和CIG4输出的有功功率依旧保持在其各自的参考值，其余的换流器型电源因受到限流器的影响，输出的有功功率均低于设定的参考值。结合图6（b）的PCC 点电压响应过程，可以轻松得出结论：CIG1运行在控制模式3 状态，而CIG4则切换至控制模式2。因此，根据控制模式1 的约束条件，CIG3产生的无功功率在出现稍许下降后很快又回到零；而其余换流器型电源则在故障发生后均产生了一定量的无功功率。特别地，虽然CIG2输出的q轴电流达到了极限值，但由于其PCC 点电压很低，故导致其向系统注入的无功功率也是相对较少的。

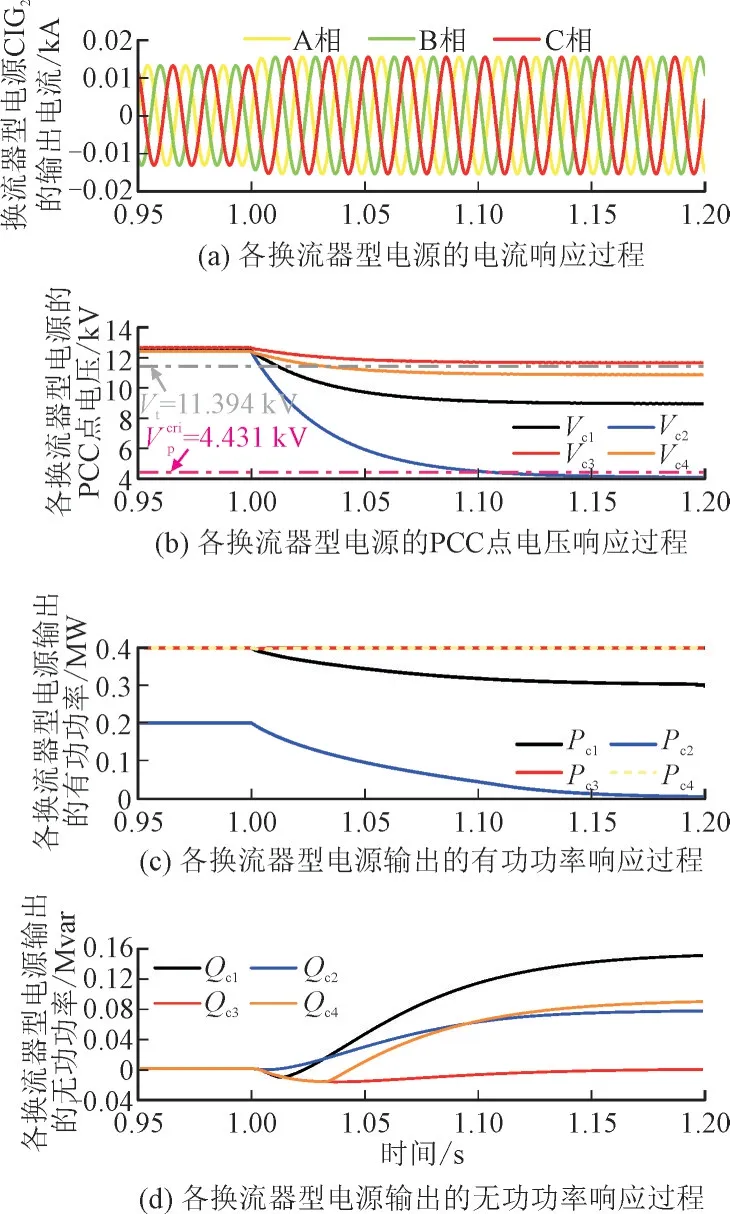
图6 各换流器型电源的故障响应过程Fig.6 Fault response of each CIG

表3 展示并对比了当f1处发生故障后，各换流器型电源PCC 点电压的仿真结果和计算结果。

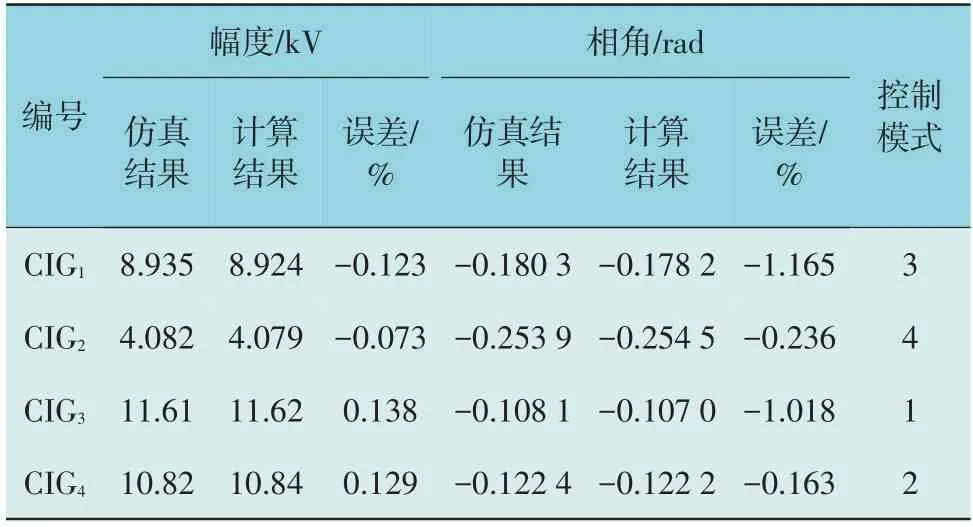
表3 各换流器型电源的PCC点电压计算结果Table 3 Calculation results of PCC voltage of each CIG

从表3 中可以看出：计算得到的各PCC 点电压的幅度和相角与仿真得到的结果误差都很小，其相对误差的绝对值均小于1.5%。这足以表明所提出的交替迭代算法在含CIGs 电力系统故障分析中具有较高的准确性。从表3 中还可以发现，由于各换流器型电源到同步电机和故障点的电气距离不同，它们所切换到的控制模式也不同；且应用该算法求得的各换流器型电源的控制模式与仿真结果一致，这也再一次验证了该算法的有效性。

3.2 算法有效性验证

图7 分析了当线路故障f1故障点处的过渡电阻rf不同时，系统的节点电压计算误差。从图7（a）中不难看出：无论f1处发生金属性故障还是非金属性故障，其节点电压幅度误差均不超过0.5%，在工程实际应用中可忽略不计。相较之下，由于一些节点的电压相角非常接近于零，而这从本质上放大了相对误差。因此，图7（b）展示的节点相角误差较幅度误差而言相对偏大，但其相对误差的绝对值的最大值也不超过4%，这也足以证明所提出的算法具有较高的精度。

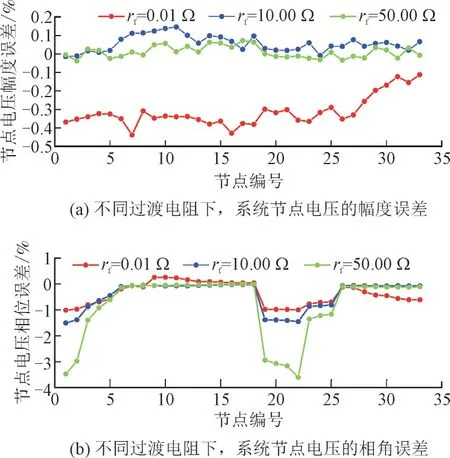
图7 过渡电阻不同时系统的节点电压误差分析Fig.7 Error analysis of node voltage with different transition resistances

图8 描绘了在不同故障场景下的节点电压计算误差折线图。如图7 所示，f2和f3分别表示发生在节点24 和节点25、节点15 和节点16 间的线路故障。从图8 中可以看出，随着故障点处过渡电阻的增加，节点电压幅度计算误差的波动范围有所减少；相对误差的绝对值大小也逐渐趋向于零。而节点电压相角误差的变化范围却随着不确定性的增加而扩大。此外，在可能的各种故障情景下，除部分异常点数据外，节点电压幅度误差和相角误差的绝对值均不超过5%，这表明了本文所提的短路电流计算分析方法具有较高的准确性。

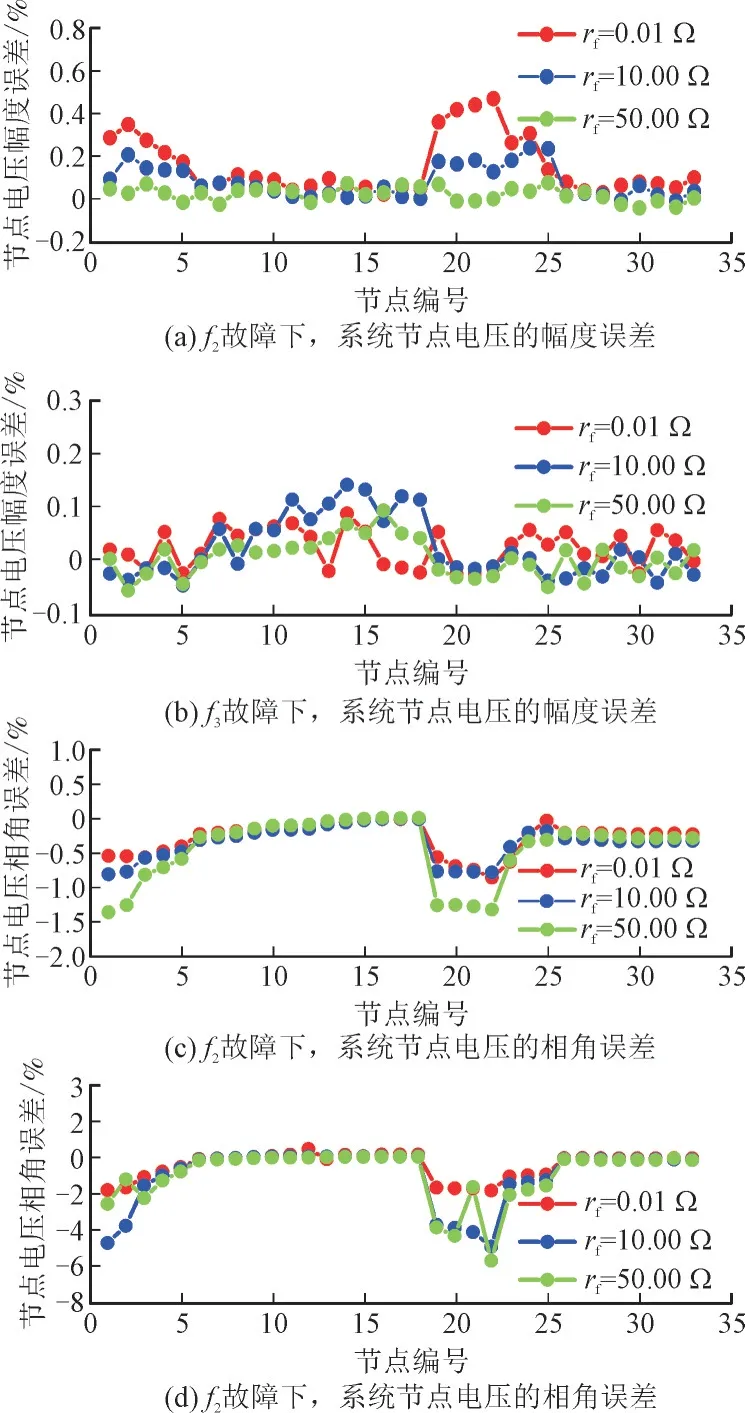
图8 不同故障条件下的计算误差Fig.8 Calculation error under different fault conditions

4 结论

本文提出了一种考虑控制模式切换的含换流器型电源电力系统短路计算方法。通过忽略并网换流器控制器的动态过程，利用等式约束和不等式约束构建了换流器型电源的电网故障分析模型。其中，等式约束可用来估算PCC 点电压和换流器输出电流；不等式约束可用于选择换流器所处的控制模式。通过交替执行估算和判别步骤，即可准确判定各换流器型电源所处的控制模式并求解故障网络。研究发现，换流器型电源的控制模式与故障位置、过渡电阻等因素密切相关。最终，通过数值仿真计算验证了所提分析方法在不同故障场景下均具有较高的准确度。