台风灾害下电力抢修队伍智能调拨技术研究

魏瑞增，王 磊，梁永超，申 原，侯 慧，朱韶华

（1.广东省电力装备可靠性重点实验室（广东电网电力科学研究院），广东广州 510080；2.广东电网有限责任公司，广东广州 510080；3.武汉理工大学自动化学院，湖北武汉 430070）

0 引言

近年来，随着全球气温升高，环境逐渐恶化，极端天气日益增加。尤其是台风天气对电力系统危害极大[1]。强风会导致杆塔倒塌、线路断线；暴雨会造成杆塔倾倒、损害变电站电气绝缘等，对电力系统正常运行造成极大危害[2-3]。所以，制定合理的电力抢修策略尤为重要[4]。

针对极端天气对电力系统正常运行造成极大危害的问题，国内外学者开展一系列研究。文献[5]提出确定电力抢修策略的关键是快速定位受损单元站点。然而，仅仅讨论受损单元的位置及数量并不能描述电力抢修过程，需要多方面来考虑。文献[6-7]分别采用粒子群及蚁群算法对电力抢修路径进行优化，提出寻找到故障点的最短路径是电力抢修的关键，并在寻找最短路径时考虑实时交通信息[8]。文献[9-10]讨论了停电负荷修复顺序，用以减少灾后负荷损失，但未考虑停电负荷的地理位置和交通状况。文献[11]讨论了分布式电源的修复策略。文献[12]提出一种基于孤岛划分及剩余网络重构的快速重构方法，提高了含分布式电源配电网的抗灾能力。这些研究都是对灾害发生之后电网抢修调拨方式进行探讨。

实际情况表明，在灾害发生后较难快速准确地获得损失信息，这种情形下进行电力抢修队伍调拨较为被动，有必要对台风造成的损失进行预测，对电力抢修队伍进行提前部署[13]。文献[14]使用应力干涉模型对输电线路损毁概率进行预测。文献[15]探讨不同因素对电网故障时空分布影响。文献[16]在比较了加速失效时间、Cox 比例风险模型、贝叶斯加性回归树及多元线性回归样条等统计模型对电力系统风暴情景下的停电时间预测精度的影响，证明贝叶斯加性回归树对飓风灾害的损失预测具有较好精度。文献[17]提出拥有更高精度的随机森林下停电时间预测模型，并指出在影响电力系统的众多因素中，最关键的因素是风暴的风特征及区域地理特征。文献[18]开发基于随机森林算法的空间广义飓风中断预测模型。文献[19]在中断预测模型的基础上引入新的两步预测程序，提高预测精度。文献[20]以随机森林算法为基础，提出台风后停电区域预测模型。文献[21]将客户画像考虑到灾害下的配电网抢修重构中来，建立兼顾客户画像和能量枢纽的配电网多目标抢修重构模型。这些文献仅是对台风造成的损失进行预测，未与灾后抢修调拨结合起来。

针对目前灾后损失信息获取相对滞后，电力抢修队伍调拨较为被动等问题，本文提出一种2 阶段台风灾害下抢修队伍的智能调拨技术，将灾前停电预测与灾后电力抢修队伍调拨结合起来。第1 阶段，使用随机森林算法对网格内停电用户数量进行预测，根据网格内停电用户数量的不同进行等级划分，提高了预测准确性。第2 阶段，根据第1 阶段预测结果，选取停电严重区域，在综合考虑经济性及效率性情况下进行电力抢修路径优化，使用NSGA-Ⅱ（Non-dominated Sorting Genetic Algorithm）算法得到帕累托前沿，并用模糊隶属度函数选取最终决策方案，可选取合适折衷解，为应急决策者提供便捷抢修指导。

1 台风灾害下电力抢修队伍的智能调拨技术框架

台风灾害下电力抢修队伍智能调拨目的是在台风来临前对区域内停电情况进行预测，并根据预测结果进行抢修任务提前规划，预先部署抢修队伍，使抢修队伍在台风到来并造成破坏后可以迅速反应，提高抢修效率。该调拨技术可分为2 个阶段：第1 阶段，将目标区域划分成1 km×1 km 网格并进行相应的数据搜集，在此基础上用随机森林算法对用户停电数量进行预测，并根据停电用户数量的不同将网格划分为4 个等级；第2 阶段，根据第1阶段预测结果，确定抢修所需工作量与时间，然后用NSGA-Ⅱ算法对抢修路径进行优化，综合考虑多方面要求，对高重要性等级网格进行电力抢修任务提前部署，并用模糊隶属度函数在帕累托前沿中选取最终决策方案。最后，用地理信息系统软件ArcGIS 对电力抢修任务分配进行可视化展示。台风灾害下电力抢修队伍的智能调拨技术模型框架如图1 所示。

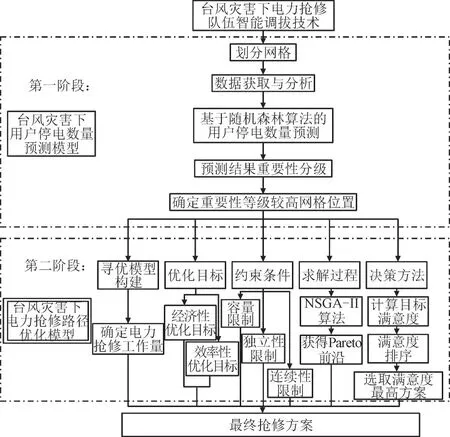
图1 台风灾害下电力抢修队伍的智能调拨技术框架Fig.1 Intelligent allocation technology framework for electric emergency repair team under typhoon disaster

2 台风灾害下用户停电数量预测模型

2.1 数据获取与分析

对预测区域进行网格划分，有助于后续抢修方案制定，而网格大小的划分格外重要。网格过大会使后续抢修队伍调拨精度不高，而过小则会使数据收集较为困难。所以，本文选取1 km×1 km 网格。对于县一级预测区域来说，1 km×1 km 网格在尽可能地保证预测准确性同时，可有效减少样本数据数量。

对网格内样本数据进行收集，台风下第z个网格样本数据如式（1）所示：

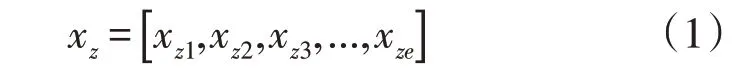
式中：e为解释变量个数；xzl为第z个网格样本中第l个解释变量的值，l=1，…，e。

式（1）中解释变量是预测模型输入变量，以预测网格样本中停电用户数量。其中包含气象因素、地理因素及电网因素等，具体如表1 所示。

表1 停电预测模型解释变量Table 1 Variables of power outage prediction model

其中，地表类型25 种，分别为水田、旱地、有林地、灌木林、疏林地、其他林地、高覆盖度草地、中覆盖度草地、低覆盖度草地、河渠、湖泊、水库坑塘、永久性冰川雪地、滩涂、滩地、城镇用地、农村居民点、其他建设用地、沙地、戈壁、盐碱地、沼泽地、裸土地、裸岩石质地、其他。下垫面类型10 种，为别为水稻土/湖泊/水库、赤红壤、红壤/滨海盐土、黄壤/酸性硫酸盐、潮土/滨海风沙土、石灰土、砂土、紫色土、石质土、粗骨土。

收集数据之后，对数据进行预处理，以保证预测结果准确性。首先剔除无效数据，即剔除掉用户数量为0 的网格，因为这些网格不会发生停电，网格上的解释变量数据已无意义。然后对剩下数据进行归一化处理，使数据映射到[0，1]区间中，归一化如式（2）所示。

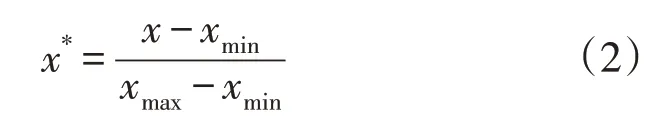
式中：x为归一化前数值；xmin和xmax分别为解释变量数据中最小值和最大值；x*为归一化后数值。

2.2 基于随机森林算法的用户停电数量预测模型

利用搜集到的数据，基于机器学习算法对用户停电数量进行预测。本文选取了随机森林算法[22]作为预测的机器学习算法。随机森林算法有很好拟合多特征变量数据的能力，可以在获得较高预测准确率的同时较好地防止过拟合。

面对真实台风情景，在综合考虑气象因素、地理因素及电网因素情况下，按照1 km×1 km 网格收集数据，并按照2.1 节方法对数据进行预处理。之后按照训练集80%和测试集20%的比例对数据进行划分，通过调节随机森林算法相关参数，使模型在测试集上的准确性较好。

在随机森林算法得到区域用户停电数量预测结果后，为了方便后续电力抢修工作展开，对停电区域重要性进行评估。通过停电区域中停电用户的多少进行重要性分级，根据分级不同确定后续电力抢修顺序以及电力抢修所需工时。重要性等级越高表明受到台风破坏越严重，所需电力抢修任务越困难。不同停电用户重要性分级情况如表2 所示。

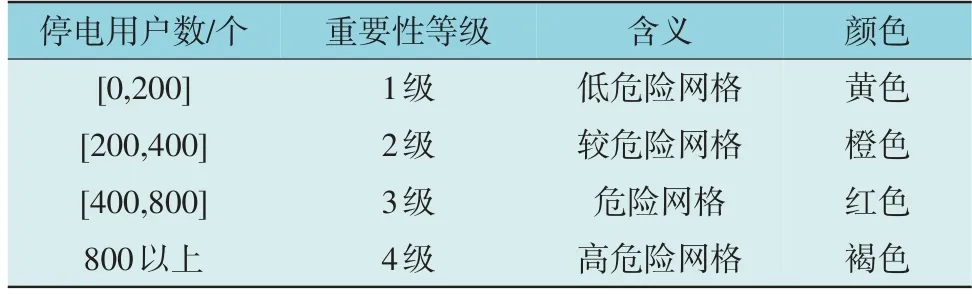
表2 重要性等级划分Table 2 Importance classification

3 台风灾害下电力抢修路径优化模型

台风灾害下电力抢修队伍的智能调拨技术第1阶段对每个网格的停电重要性进行了预测，其第2阶段根据第1 阶段的预测结果，开展电力抢修，使得台风到来后可以迅速反应排除故障，快速恢复供电。

3.1 寻优模型构建

台风灾害到来时，1 个网格内甚至会达到上千用户停电，受到电网公司维修车辆、人员及装备限制，无法实现“一对一”的电力抢修方案。1 支电力抢修队伍需要承担多个网格电力抢修任务，可以将电力抢修方案构造成车辆路径问题（Vehicle Routing Problem，VRP）进行求解。

车辆路径问题最早是由Dantzig 及Ramser 于1959 年作为卡车调拨问题提出[23]。Lenstra 及Kan在1981 年证明车辆路径问题是NP-hard 问题[24]。对于车辆路径问题的研究现已较为成熟，用其来拟合灾后电力抢修过程可减少模型复杂程度。

相对于普通车辆路径问题，台风造成的电力故障是多种多样的，对这些故障的抢修方式也有所不同。电力抢修过程消耗的多是人力而不是物力。相对于可以重复使用的工具及替换元件，电力抢修队伍付出工作量是巨大的，所以本文以抢修某受损点所需要的总抢修工时作为该点“需求量”，总抢修工时由式（3）表示：

式中：gi为修复受损点i所需总抢修工时；hi为修复节点i所需电力抢修人员数量为受损点i修复时间。

3.2 模型优化目标

本文设计目标是一个考虑多目标的台风灾害下电力抢修队伍调拨策略，在网格样本经纬度坐标及重要性等级已知前提下，对抢修路线进行寻优，寻找遍历所有受损网格并返回供电局、同时使经济性及效率性目标尽可能小的电力抢修调拨方案。

电网公司是台风灾后电力抢修的主要发起者，从供电局派抢修队伍去受损网格进行抢修。因车辆容量等限制，1 支电力抢修队伍往往无法顾及所有受损网格，所以抢修过程常要派出多支电力抢修队伍。在执行抢修任务过程中，希望最小化抢修成本，即派出最少的车辆以及总抢修路径最小化，此为经济性优化目标。

高效恢复供电同样是衡量台风灾后电力抢修任务重要指标之一，电网公司与用电用户希望用尽可能短时间恢复供电。在抢修过程中，多个电力抢修队伍被分配不同抢修任务处理不同受损点，当所有电力抢修队伍完成自己抢修任务中最后一个受损网格的修理工作后，整个区域恢复正常供电。所以，区域整体修复时间可以很好衡量抢修效率，作为效率性优化目标。

2 个优化目标定义为：

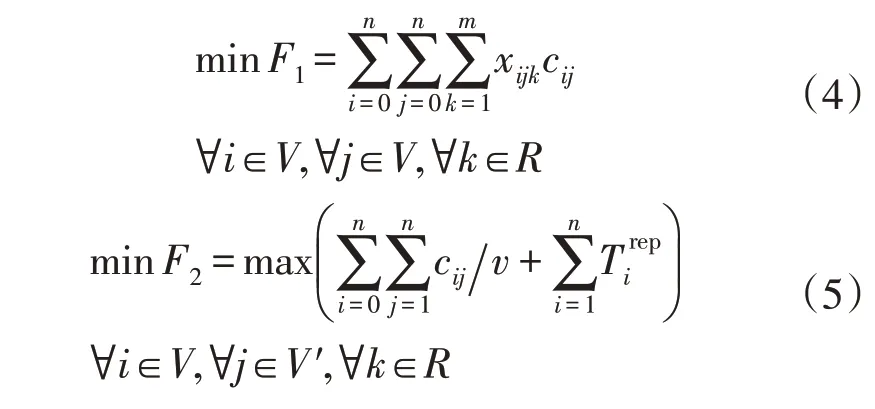
式中：F1为经济性优化目标，表示总抢修路径距离；F2为效率性优化目标，表示区域整体修复时间；xijk为决策变量，其等于1 视为电力抢修队伍k从受损点i到受损点j；cij为从受损点i到受损点j运输距离；v为行驶速度；R为抢修队伍集，是所有可调拨抢修队伍的集合；V′为包括所有受损点的集合；V为在V′的基础上添加了供电局1 个点；n为受损点数量；m为抢修车辆数量。

3.3 模型约束条件

根据台风灾害下电力抢修现实特点，对于一些容量、独立性、连续性限制，需要添加约束条件。

首先，由于抢修过程对区域整体修复时间要求较高，而对每个受损点的修复时间并无要求，所以在模型中并未给每个受损点添加时间窗限制。

其次，电力抢修队伍车辆容量有限，且电力抢修队伍精力也有限，所以每个电力抢修队伍所具备的抢修工时是有限的，有必要对此加以限制，限制条件如式（6）所示：

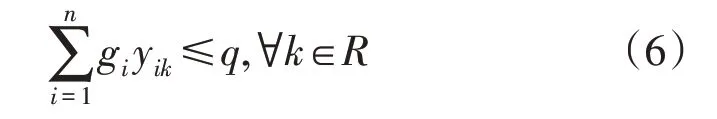
式中：yik为决策变量，其等于1 表示受损点i由电力抢修队伍k服务。

同时，为保证每个抢修队伍独立性，防止其相互影响，添加约束条件式（7）保证每个受损网格抢修任务由1 支电力抢修队伍来完成，即：

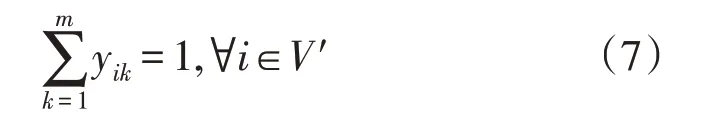
最后，为保证抢修队伍车辆运输路线连续性，添加约束条件式（8）—式（9），确保只有1 支到达和离开某受损网格的电力抢修队伍。

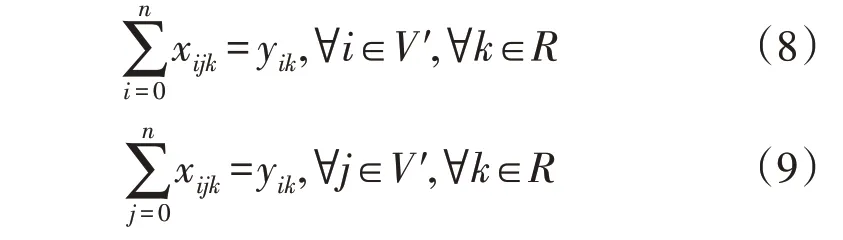
3.4 模型求解方法

NSGA-Ⅱ[25]是Deb 等人于2000 年在之前的NSGA[26]算法基础上改进而来，是一种优化的非支配排序遗传算法，在多次迭代中逼近目标非劣解集，即帕累托前沿[27]。所以NSGA-Ⅱ在解决多目标优化问题上有较好表现。NSGA-Ⅱ算法是一种遗传算法，选择适当染色体编码方式可以使问题变得简化，更容易求解。

本文跟大多数VRP 模型所用方法一样，采用RI（实整数编码），即染色体长度为受损网格数量，染色体每一位数据为受损网格编号，染色体上顺序为受损网格抢修顺序，最为重要的是染色体各位上数据是互异的。

在VRP 模型中，重要的是遍历受损网格时的顺序，而不是受损网格在染色体中位置，同时还要保证染色体上各个受损网格之间是互异的，所以本文使用顺序交叉（Order Crossover）算子[28]作为交叉算子。算子将在2 个父代中随机选择2 个切点，切点之间的点保留，切点2 边的点按照对方排列顺序从第2 个切点右侧开始排列。

同样，在拟定变异算子时，本文考虑遍历受损网格时顺序多样性变化，选择染色体片段逆转变异（Invertion Mutation）算子[29]作为变异算子，每条染色体某片段按概率进行逆转，发生逆转的片段长度是随机的，交叉及变异算子示例如图2 所示。其中，数字为染色体编号。

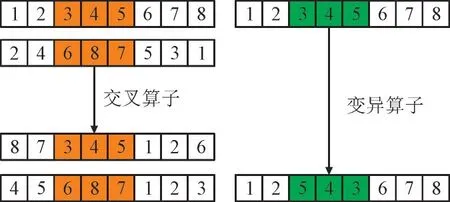
图2 交叉算子及变异算子示例Fig.2 Examples of crossover operator and mutation operator

选用该交叉及变异算子可有效捕捉父代种群中顺序关系，增加种群多样性，可以得到更好的收敛效果，有效提高求解效率。

3.5 模型决策方法

由于目标间相互制约、排斥，最终决策多目标问题的解决方案往往不是唯一的，是1 组非劣解，所以在求解完成后应加入决策者主观判断进行最终方案的选取。

通过NSGA-Ⅱ算法迭代，获得了帕累托前沿后，用模糊隶属度函数来选取最终解决方案。假设xb为帕累托前沿集合中的1 个解，其在第a个优化目标上满意程度计算方式如式（10）所示：

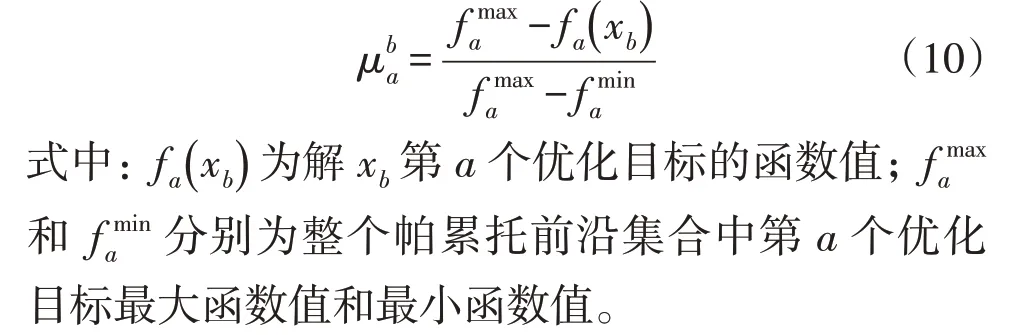
解xb对所有优化目标满意程度μb计算方式如式（11）所示：

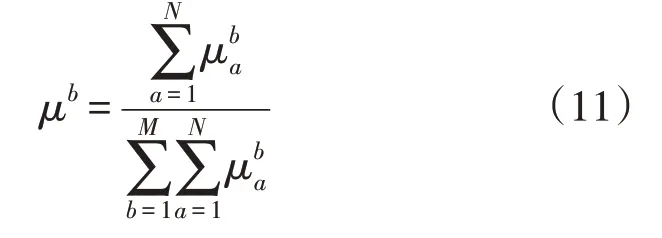
式中：M为帕累托前沿集合中解的个数；N为优化目标个数；μb值越大，证明解满意程度越高。

所以在得到帕累托前沿后，应计算每个解对所有目标满意程度，选择满意程度最大的点作为最终决策方案。

4 案例分析

台风威马逊于2014 年7 月登陆广东省，造成广东省10 kV 线路发生跳闸700 多条，28 座35 kV 及以上变电站失压，10 kV 线路倒杆（倒塔）6 507 基[30]。同年9 月台风海鸥登陆广东省，造成全省10 kV 线路发生跳闸808 条，10 kV 线路设备受损2 996 基[31]。

4.1 用户停电数量预测仿真分析

以广东省某县为例，将该县划分成1 km×1 km网格，按照网格收集相关地理信息、电网信息、台风威马逊及海鸥气象信息及2 个台风后用户停电信息，同时按照本文所述方式进行归一化处理。在对数据进行收集及处理后，选用台风威马逊数据来进行训练及测试，按照训练集80%、测试集20%比例划分数据，对台风海鸥在该县网格中停电数量进行预测。

对于随机森林算法来说，n_estimators 是最为重要的1 个参数，其含义代表着“森林”中包含决策树的个数。n_estimators 过大或者过小都会使模型预测精度降低，所以有必要对该参数进行参数优化，以拟合系数为评分标准，观察该参数从1 到200 变化时模型表现情况。模型参数优化曲线如图3 所示。

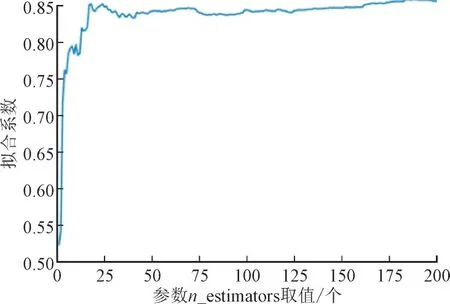
图3 随机森林算法参数优化结果Fig.3 Parameter optimizations for random forest algorithm

由图3 可知，当n_estimators 为183 时，模型的拟合系数最高。所以选取n_estimators 为183训练随机森林算法，对台风海鸥停电情况进行预测。根据停电用户数量对网格样本进行分级，并与台风海鸥真实停电情况进行对比。结果在1 641 个网格中，有1 452 个网格预测正确，正确率可达88.48%。

为直观反映台风海鸥下停电区域预测结果，使用ArcGIS 对实际停电区域及预测结果进行可视化处理，结果如图4 和图5 所示，图例中的颜色与数字对应表2 中的重要性等级。

由图4 和图5 可知，根据不同受灾情况，每个网格用电用户数量不同，重要性等级不同，颜色越深的网格重要性等级越高。大体上看，停电用户数量等级划分分布与实际停电区域分布趋势较为一致，部分网格重要性被低估。

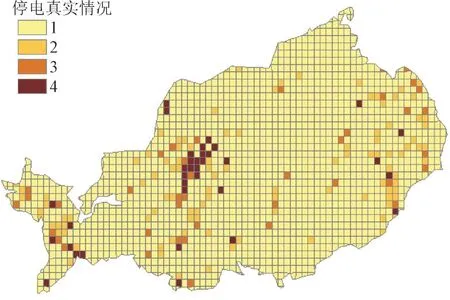
图4 某县真实停电情况可视化Fig.4 Visualization of actual power outages in a county

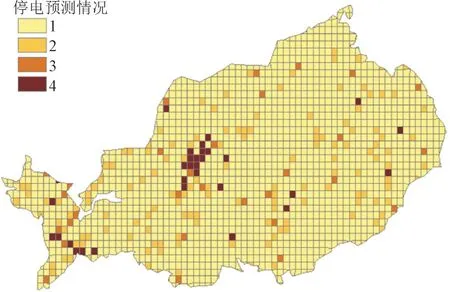
图5 某县预测停电情况可视化Fig.5 Visualization of predicted power outages in a county

4.2 电力抢修路径优化仿真分析

根据第1 阶段所得的预测结果，对于停电情况比较严重网格，尤其是重要性等级判定为等级3 及等级4 的网格，有必要进行电力抢修队伍提前部署，对电力抢修路径进行优化。停电情况严重网格地理分布如图6 所示。其中，圆点代表的是停电严重网格的中心，五角星代表的是抢修队伍出发点，即某县供电局。

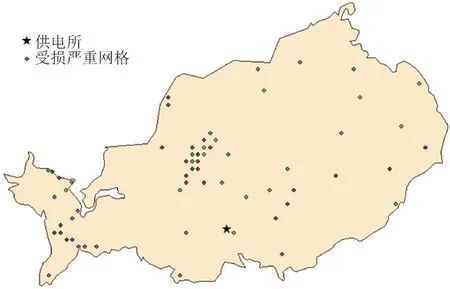
图6 停电严重网格地理分布Fig.6 Geographical distribution of grids with severe power outage

因为停电网格严重程度不同，所以修复难度也有所不同。根据现实中抢修队伍处理停电事故的情况，不同重要性等级网格所需要的抢修人数、抢修时间及抢修工时如表3 所示。

表3 不同等级抢修工时确定Table 3 Determination of rush-repair hours with different grade of importance

假设1 支电力抢修队伍有20 人，每个人可以工作15 h，每个抢修队伍抢修工时限制为300 h；考虑到台风灾害后道路交通状况变化以及暴雨对车辆行驶影响，设置电力抢修队伍车辆速度为50 km/h。为得到更好求解效果及求解速度，设置NSGA-Ⅱ算法交叉率为0.8、变异率为0.2、种群规模为100、最大迭代次数为500 代，保证算法在迭代中有较高多样性、保证解的质量同时，还可以获得较快收敛速度。使用Python 对该背景下车辆路径问题进行求解，356 s 后得到拥有100 个解的帕累托前沿，帕累托前沿分布如图7 所示。

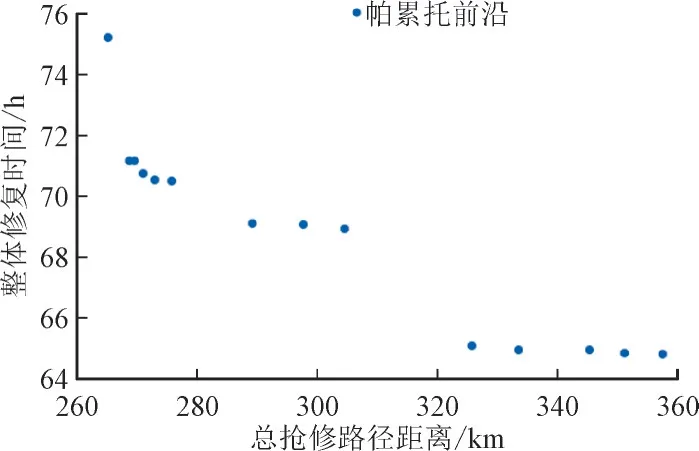
图7 帕累托前沿分布Fig.7 Pareto front distribution

从图7 可知，经济性优化目标最优解为267.79 km，但是却要接受75.21 h 区域整体修复时间；效率性优化目标最优解为64.82 h，但是要接受359.21 km 总抢修路径距离。2 个优化目标之间相互制约，未能找到同时满足2 个目标最小化的解。所以，有必要对帕累托最优解集中的解进行比较，选取在2 个优化目标上都具有较好表现的解。

根据本文介绍的模糊隶属度函数方法对每个解在各优化目标上的满意度排序，得到满意程度最高的解。通过计算，第73 个解的模糊隶属满意度最高。其总抢修路径距离为273.54 km，区域整体修复时间为69.11 h，抢修路径如图8 所示。

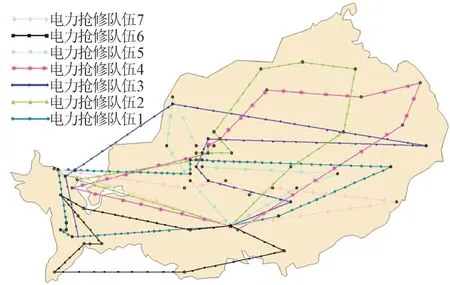
图8 电力抢修路径图Fig.8 Electric emergency repair roadmap

第73 个解所示方案将整个电力抢修任务分配给7 支电力抢修队伍，对比经济性目标最优解，该方案用经济性目标2.41%的恶化换取了效率性目标4.12%的提升。而对于效率性目标最优解，该方案用效率性目标6.62%的恶化换取了23.84%的经济性目标提升。所以，该方案是个合适折衷解。

5 结论

针对当前灾后损失信息获取相对滞后，电力抢修队伍调拨较为被动等问题。本文提出了一种2阶段台风灾害下抢修队伍智能调拨技术，通过实际案例分析得到了以下结论：

1）第1 阶段使用随机森林算法对网格内用户停电数量进行预测，并按照网格内停电用户数量对网格重要性进行分级，预测准确性可达88.48%。

2）第2 阶段使用NSGA-Ⅱ算法对电力抢修路径进行优化。最终方案用经济性目标2.41%的恶化来换取了效率性目标4.12%的提升。而对于效率性目标最优解，最终方案用效率性目标6.62%的恶化来换取了23.84%的经济性目标提升。

3）本文所提方法可以综合考虑各个目标，选择合适折衷解，为灾后抢修提供较为准确的指导。

需指出的是，未分级前随机森林算法预测精度有待提高；本文2 网格间距离的处理偏于简单，下一步可引入路网信息及实时交通信息，以便更好地贴近实际情况。