超冷(36D5/2+6S1/2)里德伯分子的制备及其电偶极矩的测量*
焦月春 白景旭 宋蓉 韩小萱 赵建明†
1)(山西大学激光光谱研究所,量子光学与光量子器件国家重点实验室,太原 030006)
2)(山西大学,极端光学协同创新中心,太原 030006)
3)(太原师范学院物理系,晋中 030619)
里德伯-基态分子由一个里德伯原子和一个基态原子组成,束缚机制是里德伯电子与基态原子的低能电子散射相互作用.理论上,通过低能电子散射Fermi 赝势模型,数值计算了铯(36D5/2+6S1/2)里德伯-基态分子的绝热势能曲线,提取了里德伯分子的束缚能和平衡核间距等光谱参数.实验上,利用双光子光缔合技术成功制备了散射三重态(TΣ,Triplet)和散射单重态-三重态混合(S,TΣ,Mixed)形成的里德伯-基态分子,获得了里德伯分子的光缔合光谱,测量的势阱深度与理论计算结果相吻合.另外,以散射三重态为例,分析了里德伯分子的光缔合光谱在外加电场中的展宽现象,获得其平均永久电偶极矩为(12.10 ± 1.65)Debye((4.76 ±0.65)ea0),与理论计算结果保持一致.该研究为实验上制备D 态里德伯-基态分子提供了可行的实验方案,对理解里德伯分子的光谱特性具有重要意义.
1 引言
正负电荷中心不重合的分子称为极性分子,具有固有电偶极矩,易于被外场操控.不同于其他由异核原子构成的分子,里德伯-基态分子是一种特殊的由同核原子构成且具有永久电偶极矩的分子,具有尺寸大和振动能级丰富等优良特性.里德伯-基态分子通常由一个里德伯原子和一个或多个基态原子通过低能电子散射相互作用束缚形成,不同于常规的共价键和离子键等,是一种全新的束缚机制.里德伯-基态分子的特殊性相对于普通极性分子而言是独一无二的,引起了国内外研究学者的广泛关注.
里德伯-基态分子的研究可追溯到20 世纪70 年代,Omont[1]在s-波散射的基础上,提出了里德伯电子可通过低能电子散射将基态原子束缚在电子轨道上形成分子的模型.2000 年,Greene等[2]进一步完善了低能电子散射理论,计算了分子的势能曲线和振动波函数,首次预言了里德伯-基态分子的存在.之后,Khuskivadze 等同样计算了由s-波散射主导形成的“三叶虫”型里德伯-基态分子[3]和由p-波散射主导形成的“蝴蝶”型里德伯-基态分子[4]的波函数,在此基础上人们详细研究了其绝热势能曲线、振动波函数以及电偶极矩等[5,6].2009 年,Pfau 研究组[7]在实验上首次实现了铷原子S 态里德伯-基态分子的制备和观测,并对其Stark 光谱和分子振动基态的寿命进行了测量.随后,人们成功地观察到铷原子nP[8],nD[9−11],铯原子nS[12,13],nP[14],nD[15−17]态里德伯-基态分子的光缔合光谱.除了上述的里德伯-基态分子之外,束缚机制为电多极相互作用形成的混合宇称的里德伯巨型分子[18,19]和由电单(多)极相互作用束缚形成的里德伯-离子分子[20−22]也是具有永久电偶极矩的特殊极性分子.这里我们主要研究铯原子里德伯和基态原子组成的双原子分子,对其余两种里德伯分子不做过多的描述.
在制备里德伯-基态分子的基础上,人们利用分子在外电场中的谱线展宽获得了里德伯分子的永久电偶极矩.Li等[23]首次测量了铷原子35S 里德伯-基态分子的永久电偶极矩为1 Debye.Niederprüm等[24]测量了铷原子25 P 态里德伯-基态分子的永久电偶极矩约为500 Debye.不同于铷原子,铯原子S 态里德伯-基态分子的永久电偶极矩高达约2000 Debye[12].由于里德伯-基态分子具有上述优良特性,因而成为研究多体气体的强相关[25]和量子信息处理[26]等的理想载体;另外,里德伯分子与负离子共振造成的DNA 链断裂[27]在医学上也有巨大的应用价值.
本文主要从理论和实验上研究了超冷铯(36D5/2+6S1/2)里德伯-基态分子的光缔合光谱.首先,利用低能电子散射理论计算了里德伯-基态分子的绝热势能曲线和振动波函数.其次,在实验上利用光缔合的方法实现了里德伯-基态分子的制备,并测量了其光缔合光谱,获得的束缚能与理论计算结果相吻合.最后,通过分子光谱在外加电场中的展宽,获得极性里德伯-基态分子散射三重态的平均永久电偶极矩为(12.10±1.65)Debye((4.76±0.65)ea0),与理论计算值保持一致.
2 理论模型
图1 所示为里德伯-基态分子的理论模型.考虑包含基态原子和里德伯原子的双原子体系,为了简化计算,假设里德伯原子核和基态原子轴矢量R的方向即为量子化轴的方向.里德伯-基态分子是由里德伯电子与基态原子通过低能电子散射相互作用束缚而形成,由Fermi 赝势描述,对应的哈密顿量表示为[9]


图1 里德伯-基态分子模型.以里德伯离子核为中心,基态原子位于轴矢量R 的位置,里德伯电子距离核的距离为r.为里德伯电子自旋,和 分别对应基态原子的电子自旋和核自旋Fig.1.Model of a Rydberg-ground molecule.The Rydberg core is located in the center,the ground atom is located at the position of the axial vectorR ,and the distance between the Rydberg electron and the core isr . is the spin of Rydberg electron,and and are the spin of the electron and nuclear of the ground atom.
里德伯电子和基态原子的散射相互作用势(r,R)表示为[1]

将总哈密顿量对角化便可获得里德伯-基态分子的绝热势能曲线W(R).进一步由于转动能级间隔远小于激发光线宽,我们忽略分子的旋转运动,利用分子哈密顿理论,通过势能曲线,可以精确地计算双原子里德伯-基态分子的振动波函数.
我们已经详细地研究了散射长度的大小、散射分波以及精细结构对绝热势能曲线和束缚势阱的影响,参见文献[16,17],这里不再赘述.图2 为数值计算的铯原子36D5/2+6S1/2(F=4)里德伯-基态分子的绝热势能曲线,计算中采用的单重态(S)和三重态(T)的零能散射长度分别为(k0)-1.92a0和(k0)-19.16a0[17],其中a0为玻尔半径.在计算中,考虑了p-波散射以及超精细结构对势能曲线的影响,图中黑色虚线是三重态散射相互作用为主形成的深势阱(TΣ,Triplet),红色实线是由单重态和三重态散射相互作用混合作用产生的浅势阱(S,TΣ,Mixed).由图2 的势能曲线可知:当R≈2100a0时,势能曲线具有最小值形成束缚势阱,可以束缚基态原子形成里德伯-基态分子;当R>2600a0时,散射相互作用趋近于零,为里德伯-基态分子的解离极限(图中黑色虚直线);当R <1600a0时,由于p-波散射的影响,势能曲线会向内层挤压,形成GHz 量级的深势阱,可形成蝴蝶型里德伯-基态分子.

图2 数值计算的铯(36D5/2+6S1/2)分子的势能曲线,彩色的波包为最外层势阱中基态υ=0 的振动波函数Fig.2.Calculated adiabatic potentials for cesium Rydbergground molecule of(36D5/2+6S1/2).The color filled wave packet is the vibration wave function of the outermost potential forυ=0 .
根据图2 计算的36D5/2+6S1/2里德伯-基态分子的绝热势能曲线,进一步计算了里德伯-基态分子的振动波函数,如图中黑色(三重态)和红色(混合态)虚线包络的高斯型波包所示为基态υ0的振动波函数:对于三重态形成的深势阱,最外层势阱势能最小值为-74.69 MHz,其包含的振动基态υ0的束缚能为-65.99 MHz;对于超精细混合形成的浅势阱,最外层势阱势能最小值为-32.65 MHz,其对应振动基态υ0的束缚能为-27.79 MHz.
由上述可知,束缚能和平衡核间距是描述里德伯-基态分子的重要光谱参数,基于上述计算结果和光谱特征,我们在实验中对其进行详细的研究,以便更好地了解和掌握分子的构成,理解其独特的束缚机制和奇特的光谱特性.
3 实验装置
图3(a)展示了双光子光缔合制备里德伯-基态分子的能级示意图.第一个波长为852 nm(Toptica DL pro)的光子实现基态 6S1/2→6P3/2的跃迁,对应的失谐量δ8522π×360 MHz,第二个波长为510 nm(Toptica TA SHG110)的光子实现里德伯激发 6P3/2→nD5/2.当第二个光子的频率调谐至里德伯-基态分子的束缚能时,里德伯电子便可束缚基态原子形成里德伯-基态分子.
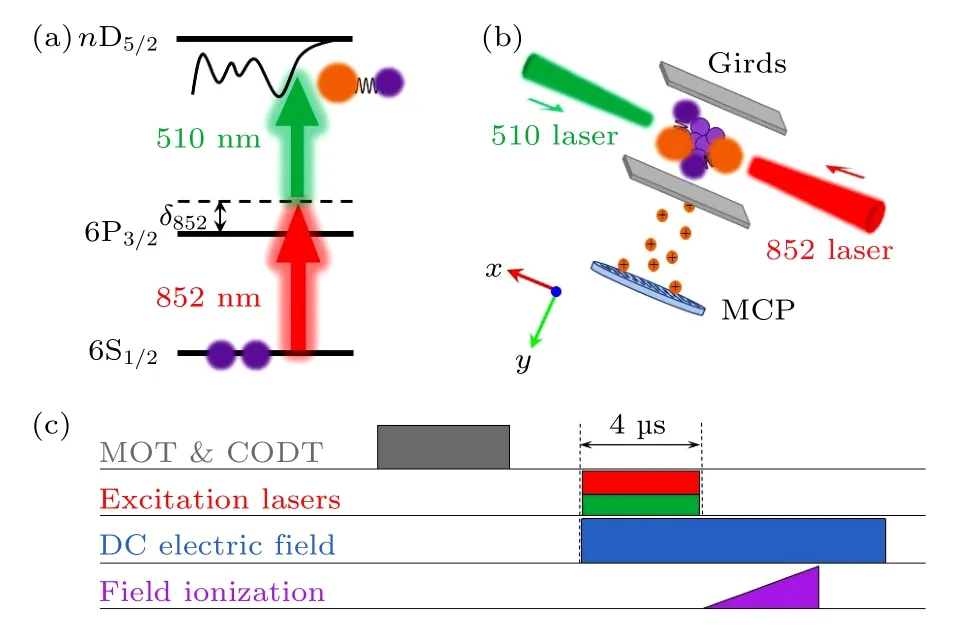
图3 (a)双光子激发能级示意图;(b)两束激发光反向传播作用于MOT&ODT 中心;里德堡原子和分子由脉冲电场电离后到达MCP,由boxcar采集和计算机记录;(c)实验时序图;关断MOT&ODT 光之后,同时打开两束激发光,之后由斜坡脉冲电离电场电离里德伯原子和分子,直流电场用于电偶极矩的研究Fig.3.(a)Schematic diagram of two photon excitation.(b)Schematic diagram of experimental set up.Two excitation lasers overlap in the center of MOT&ODT.Rydberg atoms and molecules ionized by a pulsed electric field arriving at MCP,which is collected with boxcar and recorded by computer.(c)Experimental sequence diagram.After turning off the MOT&ODT,two excitation lasers are turned on at the same time,and the Rydberg atoms and molecules were ionized by a ramp pulse ionization electric field.The direct current electric field is used to study the electric dipole moment.
我们的实验在一个交叉光学偶极阱(crossed optical dipole trap,CODT)中进行,其装载于一个标准的金属磁光阱(magneto-optical trap,MOT)中.金属腔内真空气压为 2×10-7Pa,通过吸收成像测得的基态铯原子团的峰值密度约为 2×1011cm-3,温度约为100 µK.图3(b)为实验装置示意图.腰斑为80 µm 的852 nm 的激光和腰斑为40 µm 的510 nm 的激光相向入射通过MOT中心的原子团,形成长度约600 µm 的圆柱形激发区域.利用偏振光谱稳频技术将852 nm 的激光频率精确锁定在|6S1/2,F4〉→|6P3/2,F′5〉的共振跃迁线上,由声光调制器(AOM)将其频率调谐至蓝失谐360 MHz;其次,利用Pound-Drever-Hall(PDH)稳频技术将510 nm 激光的频率锁定在精细度为15000 的Fabry-Pérot 腔上,改变电光调制器(EOM)的射频输入频率实现激发光频率的扫描.在磁光阱中心激发区域的两侧沿x,y,z三个方向各放置一对电极,其中y方向用于施加电离里德伯原子和分子的斜坡脉冲电离电场,产生的离子信号经电场加速之后到达微通道板(microchannel plate,MCP),并经过门积分器(boxcar)和数据采集卡(PCI-6733)完成离子信号的采集和记录.此外,三对电极上还施加额外的电场用于补偿系统周围的杂散电场.
为了实现里德伯-基态分子的制备,设计了如图3(c)所示的实验时序.一次实验的周期为25 ms,MOT 和ODT 光的装载时间为24.8 ms,关断MOT和ODT 光间隔10 µs 后,打开第一步和第二步激发光,完成里德伯原子的制备,与此同时,对第二步激发光的频率进行扫描.激发光的脉冲时间设置为4 µs,既能使光与原子具有充分的相互作用时间,又能避免因为相互作用时间过长而导致的谱线展宽和饱和效应.激发光关断之后,立即施加斜坡脉冲电离电场对里德伯分子和原子进行电离,并由MCP 进行离子探测,电离电场的上升沿为3 µs.
4 实验结果与分析
如图4 所示为实验测量的铯原子(36D5/2+6S1/2)里德伯-基态分子的双光子光缔合光谱.图4中零失谐的位置对应36D5/2里德伯原子的共振跃迁位置(即图2 中黑色虚线所示的零势能点),横坐标为510 nm 激光相对于共振跃迁位置的失谐量.实验数据是5 次独立测量的平均结果,误差棒为5 次测量的标准偏差.由于Franck-Condon 因子较小,测量的里德伯分子信号远小于里德伯原子信号.为了更加清晰地展示分子信号,对光谱的红失谐部分放大,如插图所示,可以清晰地看到两个里德伯-基态分子的信号,即振动基态υ0的分子信号,由红色的倒三角标记.高斯拟合可以获得分子信号的中心频率,即振动基态的束缚能为(-64.62±0.18)MHz(TΣ)和(-27.62±0.14)MHz(S,TΣ).图4中竖直的蓝线标记为理论计算的里德伯-基态分子振动基态的束缚能大小,实验测量结果与理论计算值吻合的很好,相对误差小于2.1%.实验与理论的偏差主要来源于激光的线宽,频率的校准以及系统的不确定性.

图4 铯(36D5/2+6S1/2)里德伯-基态分子的双光子光缔合光谱.红色三角形标记的峰为振动基态υ=0 的里德堡分子信号.蓝色的短线标记了理论计算的束缚势阱.插图为阴影区域的放大Fig.4.Two-color photoassociation spectra of Cs(36D5/2+6S1/2)Rydberg-ground molecule.The short blue line marks the theoretically calculated bound potential well.Red triangles denote the Rydberg-molecular signal forυ=0 .Inset is an enlargement of the shaded area.
图4 表明在实验上成功地实现了铯原子D 态里德伯-基态分子的制备.由于能级结构以及构型的独特性,同核里德伯-基态分子具有永久电偶极矩.在弱场条件下,里德伯分子的电偶极矩|d|可以由分子谱线的展宽而获得.
为了研究里德伯-基态分子光谱在外加电场中的展宽特性,只在分子束缚能附近扫描第二步激发光的频率,且在双光子激发的同时施加一个静电场,通过观察分子谱线在电场中的展宽特性,对其独特的电偶极矩进行了详细的实验研究.以散射三重态形成的里德伯-基态分子(TΣ)为例,图5 展示了电场为 0.09 和 0.37 V/cm时测量的分子光缔合光谱,误差棒显示了5 次独立实验的平均偏差.同图4中无电场时的分子光谱相比,电场中的里德伯分子光谱产生了明显的谱线展宽.

图5 电场为 0.09(a)和0.37 V/cm(b)时,三重态相互作用形成的里德伯-基态分子的光缔合光谱.红色实线为理论拟合的分子电偶极矩Fig.5.Photoassociation spectra of Rydberg ground molecules formed by triplet interaction when the electric field is 0.09(a)and 0.37 V/cm(b).Red solid line are the theoretical fitting of molecular electric dipole moment.
电场E和电偶极矩d的相互作用能表示为W-d·E,当偶极相互作用W远小于分子的束缚能时,电场的作用使分子光谱以束缚能频率为中心的非均匀展宽,表示为宽度为 2d·E/h的矩形函数.而实际的光谱展宽并不仅有上述的矩形展宽.由激光线宽和杂散电磁场导致的谱线展宽可由高斯线型函数描述,通过拟合无电场时的分子谱线获得.为了更好地拟合实验测量的分子光谱,将上述矩形函数和高斯函数进行卷积,获得有电场作用时的分子谱线为[17]
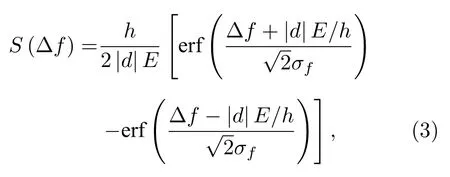
其中h为普朗克常数,Δf为相对于分子共振位置的频率失谐,erf为误差函数,σf为高斯线型的标准差.当电场E值为已知时,上述方程(3)中只有一个未知参数电偶极矩|d|,通过此方程拟合测量的分子光谱即可获得电偶极矩|d|的值.
用上述(3)式对图5 中测量的电场为0.09 和0.37 V/cm时的分子谱线进行拟合,参见图中红色实线所示,分别获得散射三重态形成的里德伯-基态分子(Triplet)的电偶极矩|d|为11.03 Debye(4.34ea0)和14.51 Debye(5.71ea0).此外,还对电场为 0.18 和 0.27 V/cm作用时的分子谱线进行拟合,最终获得三重态里德伯-基态分子的平均电偶极矩为(12.10±1.65)Debye((4.76±0.65)ea0).偶极矩的测量误差较大的主要原因是,在相同的实验条件下,随着电场增加,不仅会出现由于永久偶极矩产生的谱线展宽,同时还会出现由于Stark 效应导致的分子谱线的Stark 展宽和Stark 分裂,导致在较大电场条件下测量的偶极矩偏大,进而导致了平均测量误差较大.为了验证我们的测量结果,依据分子的绝热势能曲线,提取了径向电子绝热偶极矩D(R)和振动波函数Ψ(R),利用公式|d|计算得到三重态里德伯-基态分子的电偶极矩|d|为11.92 Debye(4.69ea0),与实验测量结果相吻合.
5 结论
本文主要研究了超冷铯原子(36D5/2+6S1/2)里德伯-基态分子的双光子光缔合光谱.理论上计算了里德伯分子的绝热势能曲线,获得了由散射三重态和散射单重态-三重态混合形成的分子束缚势阱深度和平衡核间距.实验上利用双光子光缔合的方法成功制备了(36D5/2+6S1/2)里德伯-基态分子,获得了高分辨率的分子光缔合光谱,获得了两种不同构型分子的振动基态的束缚能,实验测量结果与理论相吻合.最后,以散射三重态形成的里德伯-基态分子为例,研究了弱电场作用下的里德伯-基态分子的光谱展宽,与铯原子S 型里德伯分子(约kilo Debye)不同,D 型里德伯-基态分子的偶极矩达(12.10±1.65)Debye((4.76±0.65)ea0).这种不同主要归因于分子与里德伯电子不同轨道角动量的耦合几率不同.同核极性里德伯-基态分子展现了不同于普通极性分子的特殊性质和光谱特征,对研究里德伯分子特殊的束缚机制和奇特的性质具有重要意义.

