利用R语言进行地统计学的变异函数教学

杨孟 刁一伟

1.无锡学院环境工程学院 江苏无锡 214105；2.无锡学院大气与遥感学院 江苏无锡 214105

1 概述

地质统计学，简称地统计学，发源于矿业领域，但理论上可以对任何空间上即具有随机性又具有结构性的自然现象进行研究[1]。近年来，地统计学的应用更加广泛，从传统的地学和环境生态学领域进一步扩展到医学领域。

地统计学研究的是空间变量，因此，无论是理论还是实践教学都需要基于具有空间分析功能的软件来开展。在地统计学的教学中，通常采用的是ArcGIS软件[2]。ArcGIS软件作为一种图形界面软件，具有直观和操作简易的特点。但是，ArcGIS是一种收费软件，需要找出一种免费的替代产品。R语言[3]是统计学领域广泛使用的软件，它是基于通用公共许可协议(GNU，General Public License)进行数据处理、可视化和统计学分析的开源解释型语言，正好是一种很好的替代软件。

本文阐释了“地统计学”课程知识内容架构，并结合案例介绍了R语言在变异函数的理论和实践学中的应用，旨在展现R语言在地统计学分析中的功能，激发学生借助开源软件进行地统计分析的兴趣。

2 “地统计学”课程内容架构

“地统计学”是我校地理信息科学专业的专业课，本课程包括五个部分的内容。第一部分是回顾单变量和双变量统计分析的基础知识，介绍空间抽样的类型及其特征。第二部分是空间分析，包括传统空间分析以及空间自相关分析。第三部分是空间结构建模，包括空间变异的通用模型，随机场理论以及变异函数模型及其拟合。第四部分是克里金法，介绍常用克里金法的特点和基本假设。第五部分是通过交叉验证或者独立验证数据集对模型进行评价与优化。

3 R语言在地统计分析中的优势特征

R语言为开源免费软件，其基本内核R及作为其集成开发环境的R Studio，均可以免费下载和使用。与商业化的GIS软件相比，它的安装程序小巧，对电脑硬件要求低，具有多种操作系统版本，在系统中装载便捷且稳定可靠。

R语言具有多个地统计扩展包。R语言作为开源的解释型语言，拥有数万个用户制作和贡献的扩展程序包，其内容涵盖诸多领域，可以实现特定目的。这些扩展程序包可以在官方网站或者国内镜像网站免费下载。对于地统计分析，R语言最常用的扩展程序包是gstat，能够系统实现地统计分析的常用功能，还能与空间数据处理扩展包sp和sf兼容。另一个实现地统计分析的扩展包是georob，它具有以下特点：具有针对异常值的稳健地统计方法；使用最大似然法对参数进行估计。R语言中实现地统计功能的扩展包还有geoR和geoRglm。

地统计分析的采样点数据通常为矢量数据，因此软件对矢量数据的处理和分析能力尤为重要。R语言具有操作矢量数据的扩展包sf，其引入了空间数量分析领域通用的sf(simple features)标准规范，降低了处理、转化与绘制地理空间数据的复杂度。

4 基于R语言的变异函数案例教学

该教学内容运用R语言实现经验变异函数的计算、可视化以及拟合。使用的R扩展包有gstat、sf、sp以及ggplot2。首先，需要安装所需的扩展包及其依赖，并将扩展包加载到工作区，代码为：

4.1 加载和查看数据

在本案例中，将使用随sp包分发的Meuse土壤污染数据集。该数据集由表层土样本的重金属含量以及样本空间位置数据。利用data函数将Meuse数据集加载到工作区中：

4.2 将数据设置为空间显式的R对象

Meuse数据集为类似属性表的数据框格式，坐标还只是数据框中的字段。需要用到sf包的st_as_sf函数指定代表坐标的字段，将数据框转换为空间显式的sf对象；保留原始的数据框，并制作一个名为meuse.sf的sf对象：

从元数据中得知Meuse数据集的坐标系的EPSG代码为28992。使用st_crs函数为sf对象定义地理参考系统：

接下来，绘制锌(zinc)含量的符号图，即绘制样点位置并用符号大小表示锌含量大小，结果如图1所示：

图1 Meuse数据集中金属锌含量的符号图

4.3 变异函数建模

4.3.1 计算点对的半方差

空间中的任意两点构成一个点对，计算Meuse数据集的点最多能形成多少点对，代码如下所示，结果表明最多形成11935个点对。

半方差是指对构成点对的两个点之间属性值差异的数学度量。每个点对都可以计算一个半方差(γ)：

(1)

上式中，X表示观测点的位置，z(X)表示观测点的属性值。利用下面的代码计算数据集中前两个点的距离和半方差，可知该点对的距离和半方差分别约为70.84m以及0.001(mg/kg)2。

4.3.2 绘制变异函数云图

可以通过变异函数云展示所有点对的半方差。以下代码以logZn为变量，利用variogram函数计算距离小于200m的点对的经验变异函数云。可选参数cloud设置为TRUE时计算变差函数云；cutoff设置点对的最大距离。利用函数print绘制变异函数云图，结果如图2(a)所示。

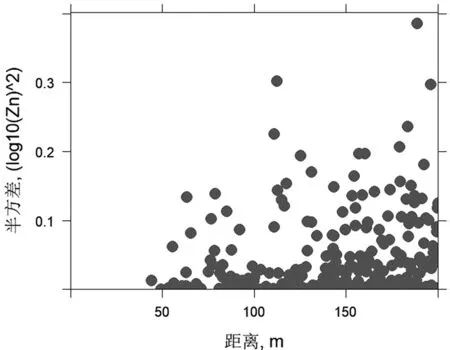
(a)最大距离200m

当最大距离增加时，见图2(b)，在半方差低值区域的许多点几乎相互重叠，此时很难通过变异函数云看出点对距离和半方差之间存在的关系。为了更好地可视化这种关系，常用方法是将点对进行分组，计算每组的半方差的算术平均值，这就是经典的马瑟隆经验变异函数：

(2)

上式中，从编号为1，2，…，i，…，j，…n的点构建点对；符号(i，j)|hij=h表示编号为i和j的点对之间的分隔向量为h。

4.3.3 确定点对分组的步长

式(2)中分隔向量h实际上是某个距离范围，而非一个特定值。通常将距离在一定范围内的点对作为一组来考虑，用来分组的距离范围称为步长。例如，将“距离为0～50m的点对”分为第1组，“距离为50～100m的点对”分为第2组，依次类推一直到最大距离1500m。此时，步长为50m、步数(组数)为30。

经验变异函数受到点对分组的显著影响。同样的变异函数云，选择的步长不同，得到的经验变异函数图也不同。步长越宽、步数越少的分组方式，具有越少的细节，越多的噪音被平滑。相反，步长越窄、步数越多的分组，具有越多的细节和噪音。R语言的variogram函数设定步长的经验法则是用最大点对距离的1/3除以15得到步长，根据该原则，Meuse数据集的步长大小应设置为100m。

以下代码针对变量logZn，绘制了一个步长为100m，最大距离1500m的经验变异函数，结果如图3(a)所示。其中，通过参数width设置步长，cutoff设置最大距离(等于步长乘以步数)；可选参数plot.numbers设置为TRUE则在点旁标准每个组的点对数。

图3中还给出了相同数据、设置不同步长时的经验变异函数图。由图可知，在相同的最大距离下，不同的步长大小对经验变异函数具有显著影响。步长100m最为合适，可以在没有噪音的情况下清楚地看出基台值、变程和块金值。太大的步长(300m)导致细节信息被过度平滑。步长太小(50m)则噪音太多，变异函数的基本特征几乎难以识别，且有些组内的点对数太少。据此，选择100m作为最佳的步长。

(a)100m

4.3.4 通过经验变异函数分析空间自相关性

经验变异函数图图3(a)提供了空间自相关的以下证据：点对间距越小，半方差越小；在某个距离范围内，半方差随着距离增加而增大，直到一个平稳状态，此时的距离称为变程；超过变程不再有空间自相关；块金值与基台值的比值(块基比)表示样本数据无法解释的空间变异的占比；块基比约为0.17，表明结构基台值的占比较大，即空间自相关的强度较大。

4.3.5 经验变异函数的拟合

接下来，需要用变异函数模型总结空间自相关性。变异函数模型是距离和半方差的连续函数，该案例选择球状模型。一旦选定了模型形式，则需要调整模型参数以获得经验变异函数的最佳拟合。首先通过目视初步估计模型参数，然后通过自动拟合对参数进行调整：

上述代码中，vgm函数用于指定一个变异函数模型。通过查看经验变异函数图图3(a)，目视估计模型参数：偏基台值psill为0.12；变程range为850；块金值nugget为0.01；指定模型形式为球状“Sph”。函数plot用于绘图，结果如图4(a)所示。

(a)目视拟合

由目视拟合结果可以看到，拟合曲线与经验变异函数不太吻合，继而使用fit.variogram函数进行自动调整：

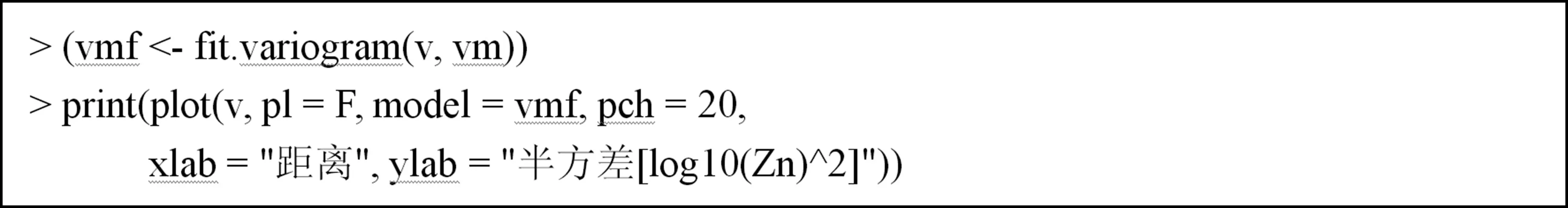
拟合得到最终的变异函数模型图4(b)表明：变程≈943m，偏基台值≈0.012，基台值≈0.111，块基比≈0.11。

结语

“地统计学”可以广泛应用于解决多个领域的空间数据预测和插值问题。变异函数是地统计学教学中的重点和难点。本文主要利用R语言的地统计学扩展包gstat，以及随sp包分发的Meuse数据集，展示了如何通过R语言进行变异函数的理论和实践教学。涉及以下步骤：计算点对半方差、绘制变异函数、确定点对分组的步长，绘制经验编译函数图并分析空间自相关性，最后拟合得到理论变异函数。该案例表明，R语言完全能够实现变异函数分析所需的功能，而且与ArcGIS这样的商业化图形界面软件相比，R语言具有更强的扩展性和灵活性，更有利于学生系统掌握地统计学的理论知识和实践技能。