一种三元线性补对偶码的构造方法

黄 山 朱士信 李 锦

①(安徽警官职业学院 合肥 230031)

②(合肥工业大学数学学院 合肥 230601)

1 引言

线性补对偶(Linear Complementary Dual,LCD)码是一类具有特殊结构的线性码，它由Massey[1]引入并用于解决数据的有效存储。1992年，Massey[2]证明LCD码为双用户加法器信道提供了一种最佳的线性编码方案。2014年，Bringer等人[3]将2元LCD码用于抵抗侧信道攻击和错误注入攻击。2016年，Carlet和Guilley[4]将q元LCD码用于抵抗侧信道攻击和错误注入攻击，并给出了几种LCD码的构造方法。鉴于LCD码在抵御侧信道攻击和错误注入攻击方面的重要应用，LCD码的研究是一项重要的工作。2017年，Li等人[5,6]构造了循环LCD码，并确定了它们的参数。2018年，Sok等人[7]利用正交群、码的扩展和矩阵积码构造了大域上LCD码。2019年，Liu等人[8]利用有限域上典型群构造了LCD码。2021年，Shi等人[9]利用有限域上托普利兹矩阵构造了LCD码。最近，唐春明等人[10]总结了有限域上LCD码的一些主要成果和进展，并提出了此研究领域的一些未解决的重要问题。与此同时，有限域上LCD极大距离可分(Linear Complementary Dual Maximum Distance Separable, LCD MDS)码的构造也得到了深入的研究。最近，金玲飞等人[11]总结了有限域上LCD MDS码的一些主要成果和进展。除此之外，有限环上LCD码的构造也得到了深入的研究[12-15]。

2018年，Carlet等人[16]证明：给定参数为[n,k,d]的q元线性码，当q＞3时，存在一个与其等价的具有相同参数的q元LCD码。此后，2元和3元LCD码的构造受到重点关注。2017年，Rao等人[17]利用循环码构造了一些参数好的2元LCD码。2018年，Seneviratne和Melcher[18]利用几何的方法分别构造了一类2元和3元LCD码。2019年，Zhou等人[19]利用定义集方法构造了参数优的2元LCD码。Carlet等人[20]利用正交或辛基刻画了2元LCD码并研究了2元LCD码的最小距离。Galindo等人[21]利用J-仿射变种码的子域子码，构造了参数好的2元和3元LCD码。Li等人[22]利用定义集方法构造了参数优的3元LCD码。Liu等人[23]确定了几类长度为2m+1的2元线性补BCH(Linear Complementary Dual Bose Chaudhuri Hocquenghem, LCD BCH)码的参数。2020年，Wu等人[24]利用单纯复形构造了参数优的2元LCD码。Huang等人[25]构造了一类长度为2m-1的LCD BCH码并研究了这类码的参数。Lu等人[26]利用拓展、截断和组合等方法，构造了参数好的3元LCD码。2021年，Bouyuklieva[27]研究了2元LCD码的性质及其最大极小重量的界。Araya等人[28]给出了2元和3元LCD码的最大极小重量的一个刻画，并分类了小维数的最优2元和3元LCD码。Harada[29]给出了2元和3元LCD码的两种构造方法，并改进了这两类LCD码的最大极小重量的界。Araya等人[30]分别确定了维数为5的2元LCD码和维数为4的3元LCD码的最大极小重量。2022年，Liu等人[31]利用矩阵积码，构造了渐近好的2元和3元LCD码。Huang等人[32]确定了一些3元长度为 3m-1的LCD BCH码的重量分布。最近，李平等人[33]利用定义集方法构造了一些参数优的3元LCD码。从研究现状分析，构造参数好的3元LCD码是一个有趣的问题。

本文利用环 F3+uF3(u2=0)上循环码的Gray象构造3元LCD码。环 F3+uF3是一类有限链环。Dinh等人[34]确定了有限链环上循环码的代数结构。Norton等人[35]证明有限链环上线性码的Hamming距离等于其最高阶挠码的Hamming距离。张付丽等人[36]确定了环Fq+uFq上循环码的剩余码和挠码的结构，并将其应用于构造量子码，其中u2=0且q是一个素数幂。本文通过引入( F3+uF3)n到F23n的等距Gray映射，利用环F3+uF3上长度为n的循环码的Gray象，构造了几类长度为 2n的参数好的3元LCD码。

2 预备知识

引理2[34]设n是一个正整数且g cd(n,3)=1。设C是环F3+uF3上长度为n的循环码，则存在唯一的首一多项式f(x)和h(x)使 得C=(f(x)h(x),uf(x))，其中f(x)h(x)|(xn-1)。

文献[36]研究了环 Fq+uFq上循环码的挠码，其中u2=0 且q是一个素数幂。将相关结果应用到F3+uF3上循环码，有如下结论。

引理3[36]设n是一个正整数且g cd(n,3)=1。设C=(f(x)h(x),uf(x))是 环F3+uF3上长度为n的循环码，其中f(x)和h(x) 是F3上首一多项式且f(x)h(x)|(xn- 1) 。 则 R es(C) = (f(x)h(x))且Tor(C)=(f(x))。

3 3元LCD码的构造

证明 由引理3， Res(C)=(f(x)h(x))。因为f(x)h(x)∈C，所以R es(C)⊆C。一方面，由引理1，R es(C)∩Res(C)⊥={0}当 且仅当(f(x)h(x))*=f(x)h(x) 。容 易 验 证，(f(x)h(x))*=f*(x)h*(x)。因此， (f(x)h(x))*=f(x)h(x) 等价于f*(x)h*(x)=f(x)h(x)。 另一方面，由引理3，T or(C)=(f(x))。由引理1，T or(C)∩Tor(C)⊥={0}当 且仅当f*(x)=f(x)。综合两方面，结论成立。 证毕

引理5 设C=(f(x)h(x),uf(x))是 环R上长度为n的循环码，其中f(x)和h(x) 是F3上首一多项式且f(x)h(x)|(xn-1) 。则C的G r a y 距离dG满足：min{d1,2d2}≤dG≤2d2， 其中d1和d2分 别是Res(C)和T or(C)的Hamming距离。

证明 设c(x)=a(x)+ub(x)∈C且c(x)̸=0。由引理4，R es(C)⊆C，所以a(x)∈Res(C)且b(x)∈Tor(C)。由Gray重量的定义

其中， (-|-) 表示向量的级联。当a(x)=0时，b(x)̸=0 且wtG(c(x))=2·wtH(b(x)) 。 由 于b(x)∈Tor(C) ，所以w tG(c(x))≥2d2。当a(x)̸=0时，注意到

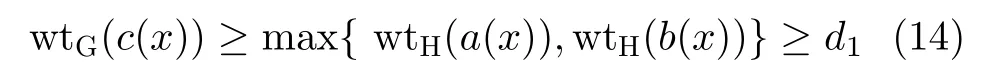
因此，w tG(c(x))≥min{d1,2d2}， 即dG≥min{d1,2d2}。特别地，因为T or(C)的 Hamming距离为d2，所以存在λ(x)∈Tor(C)使 得w tH(λ(x))=d2。 注意到uλ(x)∈C且 wtG(uλ(x))=2d2， 因此，dG≤2d2。 证毕

由引理4和引理5，利用环R上循环码可以构造如下参数的3元LCD码。

定理2 设f(x)和h(x)是 F3上首一多项式且使得f(x)h(x)|(xn-1),f*(x)=f(x)且h*(x)=h(x)。 设d1和d2分 别 是 长 度 为n的3 元 循 环 码(f(x)h(x))和(f(x))的 Hamming距离。设C=(f(x)h(x),uf(x))是环R上长度为n的循环码，则ϕ(C) 是3元[2n,2n-2 deg(f(x))-deg(h(x)),d]L CD码，其中min{d1,2d2}≤d ≤2d2。

证明 由引理3，R es(C)=(f(x)h(x))且 Tor(C)=(f(x))。 当f*(x)=f(x)且h*(x)=h(x)时，由引理4，Res(C)⊆C且Res(C)∩Res(C)⊥=Tor(C)∩Tor(C)⊥={0}。由定理1，ϕ(C) 是长度为2n的LCD码。码ϕ(C)的维数由引理5，码C的Gray距离dG满足min{d1,2d2}≤dG≤2d2。由 定 理1，码ϕ(C)的H a m m i n g 距 离d=dG。综上所述，结论成立。 证毕

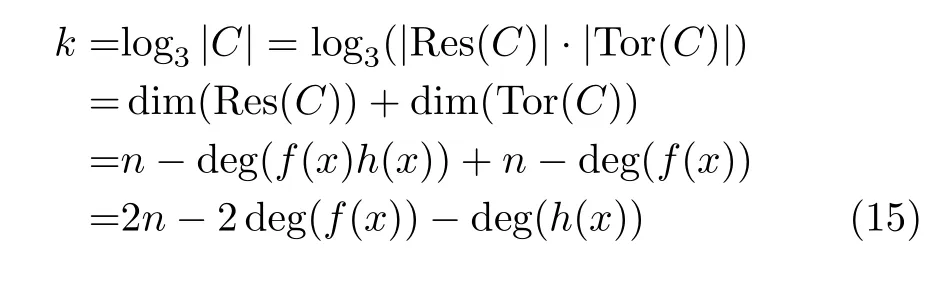
定理3 设n是一个正整数且存在j使得3j ≡-1(modn) 。设m是 使 得3m ≡-1(modn)的 最小正整数。设β是一个n次 本原单位根且M(x)是β在F3上 的极小多项式。设C=((x-1)M(x),u(x-1))是环R上长度为n的循环码，则ϕ(C) 是 3元[2n,2n-2m-2,4] L C D 码，且R es(C) 是3 元[n,n-2m-1,d ≥4]LCD码。

证明 显然， (x-1)*=x-1 。因为存在j使得3j ≡-1(modn) ，所以M*(x)=M(x)。又因为m是使得3m ≡-1(modn)的最小正整数，所以ordn(3)=2m， 即d eg(M(x))=2m。 由定理2，ϕ(C)是一个3 元 [2n,2n-2m-2]L C D 码。由 引 理3，Res(C)=((x-1)M(x)) ， 则R es(C) 是3 元[n,n-2m-1] LCD码。下面讨论ϕ(C) 和R es(C)的Hamming距离。

显 然， Tor(C)=(x-1)的H a m m i n g 距 离d2=2 。设d1是R es(C)的Hamming距离。注意到3m ≡-1(modn)， 即β-1是M(x)的 零点。进而，β-1,β0,β是(x-1)M(x)的 零点。由BCH界[37]，d1≥4。综合两方面，由定理2，ϕ(C)的Hamming距离d=4。 证毕

由定理3，可以得到如下两类具体的LCD码。

推论1设n=3m+1 ，其中m为整数。设β是一个n次本原单位根且M(x)是β在F3上的极小多项式。设C=((x-1)M(x),u(x-1)) 是 环R上长度为n的循环码，则ϕ(C) 是 3元[2·3m+2,2·3m-2m,4]LCD码，且剩余码 Res(C)=((x-1)M(x))是3元[3m+1,3m-2m,d ≥4]LCD码。

下面分析定理3构造的LCD码的性能。当[n,k,d]LCD码用于抵御侧信道攻击时，零偏移遮蔽对策是d-1阶 安全的。当[n,k,d]LCD码用于抵御错误注入攻击时，任何一个Hamming重量严格小于d的错误都可以被检测出来。因此，对固定的长度n和 维数k，构造Hamming距离尽可能大的LCD码

是环R上长度为 10 的 循环码。由推论1，ϕ(C)是3元[20,14,4]LCD码，且R es(C)是3元[10,5,4] LCD码。因为不存在3元[ 20,14,d ≥5]线 性码，ϕ(C)的Hamming距离达到了最大值，所以ϕ(C)是最优的3元LCD码。由码表[39]，长度为 10 维数为5 的3元线性码的Hamming距离的最大值为5 。 因此，R es(C)是几乎最优的3元LCD码。

例3 设β ∈F36是x6+2x5+2x3+2x+1的一个零点，则β是一个2 8次本原单位根。设

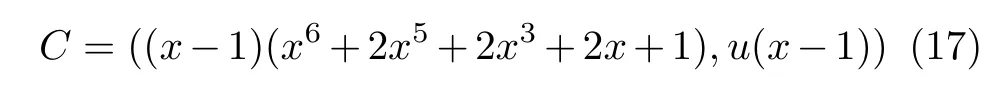
是环R上长度为 28 的 循环码。由推论1，ϕ(C)是3元[56,48,4] L C D 码，且R es(C)是3 元[2 8,2 1,4]LCD码。根据理论界，长度为 56 维数为4 8的3元线性码的Hamming距离d ≤5。由码表[39]，长度为56 维 数为4 8的3元线性码的Hamming距离的已知最大值为 4。因此，ϕ(C)是已知参数最好的3 元LCD码。同理，由码表[39]，长度为 28 维数为 21的3元线性码的Hamming距离的已知最大值为4。因此，R es(C)也是已知参数最好的3元LCD码。

定理4 设n是3m-1的 正因子且n＞3m/2+1，其中m≥2 为 正整数。设β是一个n次本原单位根且M(x)是β在F3上 的极小多项式。设C=((x-1)M(x)M*(x),u(x-1)) 是环R上长度为n的循环码，则ϕ(C)是 3元[ 2n,2n-2m-2,4] L CD码，且R es(C)是3元[n,n-2m-1,d ≥4]LCD码。

证明 设 ordn(3)=e。因为n整除3m-1，所以e整除m。当e＜m时

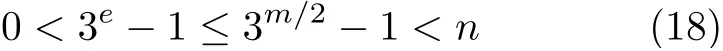
这 与n整 除3e-1 矛 盾。 因 此，deg(M(x))=deg(M*(x))=m。下面证明M(x)̸=M*(x)。假设M(x)=M*(x)， 则β-1是M(x)的零点，其等价于存在0≤j ≤m-1 使 得- 1≡3j(modn) 。 当0≤j≤m/2时 ，0＜3j+1≤3m/2+1＜n， 矛盾。当m/2+1≤j ≤m-1 时 ，- 1≡3j(modn) 与-3m-j ≡3m ≡1(modn)等 价。同理，0＜3m-j+1≤3m/2-1+1＜n， 矛盾。因此，Res(C)=((x-1)M(x)M*(x))且Tor(C)=(x-1)。 与定理3类似可证，T or(C)的Hamming距离d2=2 ，R es(C)的Hamming距离d1≥4 。由 定 理2，ϕ(C) 是3 元[2n,2n-2m-2,4]LCD码。由引理1，R es(C)是 3元[n,n-2m-1,d ≥4]LCD码。 证毕

由定理4，可以得到如下两类具体的LCD码。

推论2设n=3m-1，其中m≥2为正整数。设β是一个n次 本原单位根且M(x)是β在F3上的极小多项式。设C=((x-1)M(x),u(x-1)) 是 环R上长度为n的循环码，则ϕ(C) 是3元[2·3m-2,2·3m-2m-4,4] L C D 码，且R es(C) 是3 元[3m-1,3m-2m-2,d ≥4]LCD码。

下面分析定理4构造的LCD码的性能。基于以上分析，对于抵御侧信道攻击和错误注入攻击，对固定的长度n和 维数k，构造Hamming距离尽可能大的LCD码是一个重要的问题。当n=3m-1时，由Hamming界，长度为n、 维数为n-2m-1的3元线性码的Hamming距离d≤6。由界(2)，不存在3元[n,n-2m-1,6]线性码。因此，根据线性码的理论界，长度为n、 维数为n-2m-1的3元线性码的Hamming距离d≤5。同理，根据线性码的理论界，当n=2(3m-1)时 ，长度为n、 维数为n-2m-2的3元线性码的Hamming距离d ≤5。因此，推论2构造的两类3元LCD码的Hamming距离与理论界相差1，具有较好的参数。一方面，与线性码的理论界比较，定理4可以构造参数好的LCD码。另一方面，与码表[39]比较，定理4可以构造已知参数最好的LCD码。下面给出两个具体的例子加以说明。

例4设β∈F32是x2+2x+2的 一个零点，则β是 8次本原单位根。显然，(x2+2x+2)*=x2+x+2。设C=((x-1)(x2+2x+2)(x2+x+2),u(x-1))是环R上长度为8 的循环码。由推论2，ϕ(C)是3元[16,10,4] LCD码，且R es(C)是3元 [8,3,4] LCD码。由码表[39]，不存在3元[ 16,10,d ≥5]线性码，因此ϕ(C)是最优的3元LCD码。同理，由码表[39]，长度为8维数为3的3元线性码的Hamming距离的最大值为5。因此，R es(C)是几乎最优的3元LCD码。

例5设β ∈F33是x3+2x+1的一个零点，则β是2 6次本原单位根。显然

最后，将本文构造的3元LCD码与现有文献进行比较。文献[18]利用组合的方法构造了3元

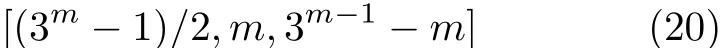
LCD码。文献[21]利用J-仿射变种码的子域子码，构造了长度满足一定约束条件的3元LCD码。文献[22]利用定义集方法构造了几类LCD码。文献[26]构造了长度n≤20的3元LCD码。文献[33]利用定义集方法构造了Hamming距离为3的最优LCD码。通过比较发现，本文构造了新参数的3元LCD码。与线性码的理论界和码表比较，本文构造的4类3元LCD码具有较好的参数。

4 结束语

造Hamming距离大于4的最优3元LCD码是进一步的研究问题。