基于部分积概率分析的高精度低功耗近似浮点乘法器设计

闫成刚 赵 轩 徐宸宇 陈 珂 葛际鹏 王成华 刘伟强

(南京航空航天大学电子信息工程学院/集成电路学院 南京 211106)

1 引言

近半个世纪以来，得益于半导体工艺的发展，集成电路的工作速度与能效一直在不断提高[1]。然而，随着半导体工艺技术的发展速度逐渐放缓[2]以及Dennard缩放比例定律趋于失效，集成电路的能耗与效率面临严峻的挑战。作为一种新兴的计算范式，近似计算为解决集成电路的高能耗问题提供了新的思路[3]，即通过牺牲适当的精度来换取相当可观的能耗收益。对于数据识别、图像处理、机器学习及无线通信等具有一定容错能力的应用，即使引入近似计算会带来一些精度下降，也能产生合理的结果[4]。例如，文献[5]提出了一种低电压、低面积、低漏电功耗、采用精度自适应近似计算单元的超低功耗二值化权重网络加速器，相较于现有技术，功耗降低约1.7倍。文献[6]提出了一种用于低功耗语音关键字识别的精度自适应的Mel频率倒谱系数(Mel Frequency Cepstrum Coefficients,MFCC)架构，可以根据输入语音背景噪声动态配置为使用具有不同硬件设置的两种计算模式，功耗最多可降低76.3%，并且将精度提高了0.8%，有效促进了近似计算在低功耗语音处理芯片中的应用。因此，近似计算有着良好的应用前景与广泛的应用范围。

相较于定点数，浮点数的动态范围更大，因此被广泛应用于高动态范围(High-Dynamic Range,HDR)图像处理及无线通信等领域。作为一种常用的浮点算术运算单元，浮点乘法器的复杂度高、硬件资源消耗大，在具有容错特性的浮点应用中使用近似浮点乘法器可以有效降低系统功耗。目前对近似浮点乘法器的研究工作主要是针对尾数乘法的近似设计。尾数乘法与定点乘法相似，可根据定点乘法器的近似思路对其进行设计。定点乘法器作为最基本的算术运算单元之一，相比于加法器等单元有着相对复杂的算法和结构，是近似电路的主要研究对象[7]。目前主流的乘法器设计包括部分积生成、部分积压缩以及最终求和部分。其中乘法器的功耗主要集中在前两部分，因此近似乘法器也主要针对这两部分进行优化设计。基于改进基-4 Booth编码器，文献[8]通过修改Booth编码设计的卡诺图来简化编码器结构，并提出近似基-4 Booth编码器以满足不同程度错误及硬件性能要求。虽然近似Booth乘法器通过降低部分积的行数能够有效提高速度，且近似Booth编码器能带来一定的面积与功耗的收益，但会导致部分积生成模块面积增加。文献[9-14]对压缩器结构进行逻辑简化，对压缩器结构优化并对其错误进行分析，提出多种近似4-2,5-2及6-2压缩器。文献[15]在提出3种新型近似4-2压缩器的同时，提出了纠错模块以取得误差性能与资源消耗的折中。但是以上近似压缩器均存在出错情况较多，输出结果受输入顺序影响的问题，仅适用于部分积中1的概率全部相同的场景，有一定的局限性。虽然定点乘法器已从部分积生成、部分积压缩方面进行了大量研究，但是关于浮点乘法器近似设计的研究还不充分。文献[16]提出了一种应用于神经网络训练的浮点对数乘法器设计，通过将尾数乘法转换为对数域的加法来实现尾数相乘，相较精确浮点乘法器面积减少10.7倍。文献[17]对浮点乘法器的尾数乘法部分的表达式进行重新整合并根据精度要求对其进行简化，提出一种可配置的近似浮点乘法器。上述两种近似浮点乘法器的硬件收益较大，但由于近似程度较大仅适用于错误容忍度较高的场景。文献[18]通过调整尾数乘法部分的部分积截断位置以及压缩树结构中近似压缩器的使用位宽来实现适用于不同精度要求的多种近似浮点乘法器设计，并指出其中综合性能最好的近似设计。但是上述设计均未考虑部分积为1的概率分布，当概率分布不同时可能会引入额外的误差。

针对现有近似浮点乘法器误差大且受输入顺序影响的问题，本文对浮点乘法器中的部分积为1的概率进行分析，并提出一种近似4-2压缩器及低位或门压缩的方法。然后，给出近似尾数乘法器的压缩结构并将其应用在近似浮点乘法器中。最后，分别对近似尾数乘法器及近似浮点乘法器进行误差、硬件功耗的评估并将其用于高动态范围图像处理。通过对比之前的近似设计，本文提出的基于部分积概率分析的近似浮点乘法器在精度相当的情况下有效降低了浮点乘法器的硬件资源消耗、功耗以及延时，具有较高的应用价值。

2 浮点乘法器

根据IEEE 754-2008标准[19]，半精度浮点数由16位表示。规格化半精度浮点数分为符号位(Sign)、指数部分(Exponent)和尾数部分(Mantissa)3部分。其中第15位为符号位，1表示为负，0表示为正；第14位-第10位为指数部分，其中偏置量为15，实际的指数为E-15；最后第9位-第0位为尾数部分，是尾数的小数部分，包括隐含位的尾数为1.M。因此，规格化浮点数N可表示为式(1)

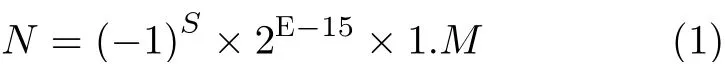
其中，1.M表示整数部分恒为1的任意小数。

浮点乘法器结构如图1所示。首先将两个操作数的符号位进行异或得到结果的符号位，然后对操作数的尾数相乘并进行规格化及舍入得到最终的尾数结果，接着将操作数的指数相加并根据舍入情况进行指数调整，最后将符号位、指数部分和尾数部分进行拼接得到最终输出结果。此外，通用浮点乘法器还应包含对无穷、非数、非规格化数等特殊情况的处理。

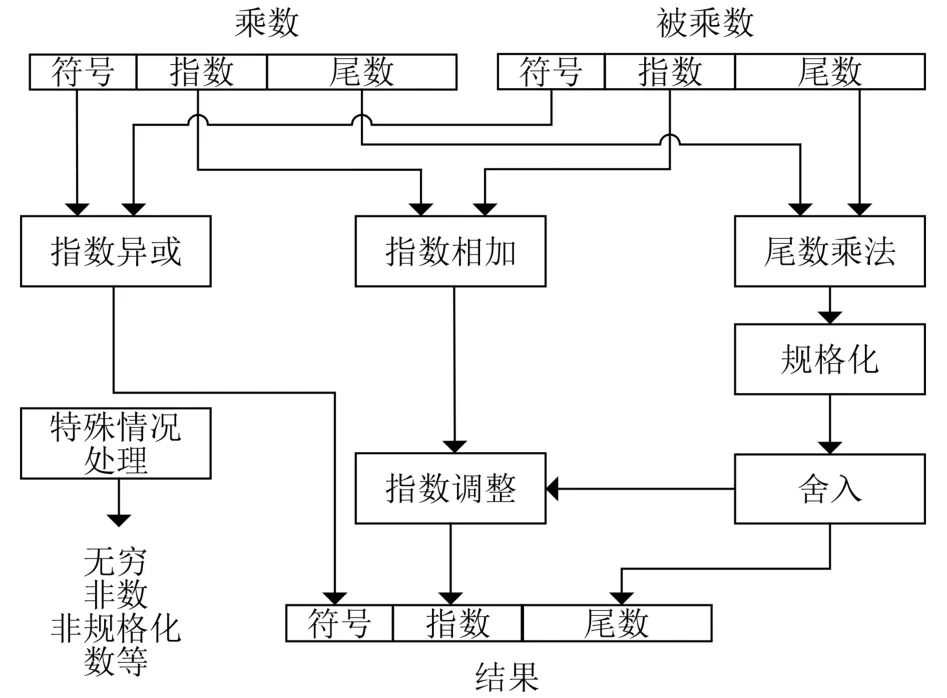
图1 浮点乘法器结构

3 基于部分积概率分析的近似浮点乘法器

浮点乘法器中包括多个模块，其中尾数乘法部分的硬件功耗占比最大。以单精度浮点乘法器为例，其24位尾数乘法的硬件功耗占总体功耗的80%以上[20]。因此，本文主要针对浮点乘法器中的尾数乘法模块进行近似设计，以获得整体的收益。在浮点乘法器中，结果的符号由两个操作数的符号位进行异或得到，尾数乘法为无符号定点乘法。以半精度浮点数为例，包括隐含位的尾数为11位，基于部分积为1的概率分析，提出了一种近似4-2压缩器及低位或门压缩的方法，实现了高能效的近似浮点乘法器。

3.1 尾数乘法的部分积概率分析

高斯分布作为普遍的数据分布规律，同时HDR图像处理及无线通信等应用中数据均为高斯分布，因此对高斯分布数据的运算规律进行分析非常重要。对高斯分布的浮点数的尾数中1的概率进行实验统计，分布如表1所示，其中A为包括隐含位的11位尾数。从表中可以看出：尾数最高位为1的概率高达0.97，与浮点数绝大多是规约数的情况相符；浮点数的尾数为无符号数，尾数随着数值增大概率逐渐降低，与原始数据分布规律一致，均为高斯分布。

表1 浮点数的尾数中1的概率

浮点数的尾数中1的分布概率不同将导致尾数乘法的部分积为1的概率分布不均匀，因此在尾数乘法中根据部分积概率分布进行优化，以引入尽可能少的错误。

3.2 一种近似4-2压缩器

通过两个全加器(Full Adder, FA)串联实现的传统精确4-2压缩器(5个输入为P4, P3, P2, P1,Cin, 3个输出为Sum, Cout, Carry)的电路结构如图2所示，其中全加器的结构如图3所示。

图2 传统精确4-2压缩器

图3 全加器

该精确4-2压缩器的关键路径延时为两级全加器，即4级异或门[21]。近似压缩器设计通常将低位进位Cin及高位进位Cout舍弃，并在此基础上修改压缩器真值表来实现更简单的逻辑功能，从而简化压缩器的结构。其中，文献[22]对压缩器的真值表进行大幅度简化并提出一种称为Ahma的近似4-2压缩器，结构如图4所示。Ahma仅需3个或非门和1个与非门，能显著降低面积、延时和功耗。Ahma存在出错情况多且错误大小及方向与输入顺序有关的不足，仅适用于容错程度高的应用或低权重位的压缩。

图4 Ahma近似4-2压缩器[22]

考虑到现有近似4-2压缩器在某些特定输入会产生错误输出，在各输入概率不相等的情况下出错的概率可能会偏高。因此可通过调整输入顺序以保证产生错误输出对应的输入概率最低[23]，但是该设计方法拓展性差，不适合大规模电路的设计。基于部分积为1概率分析，本文提出一种对输入顺序不敏感的近似4-2压缩器。该近似4-2压缩器的4个输入为P4, P3, P2, P1, 2个输出为Sum, Carry，其电路原理如图5所示。该结构包括3个异或门、3个与门及1个三输入或门，关键路径延时为1级异或门、1级与门及1级三输入或门。参照文献[24]及表2的对比情况可见，本文提出的近似4-2压缩器的归一化延时为传统精确4-2压缩器的60%，极大降低了压缩器的延时。

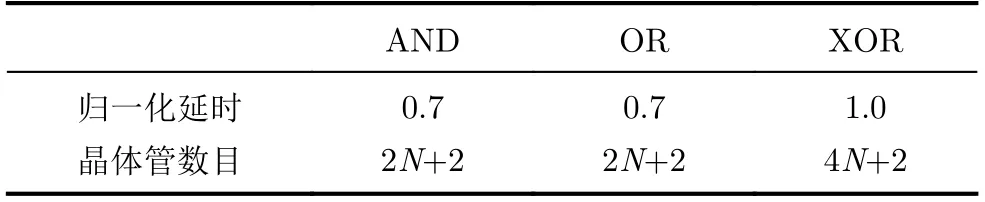
表2 门电路的延时[24]

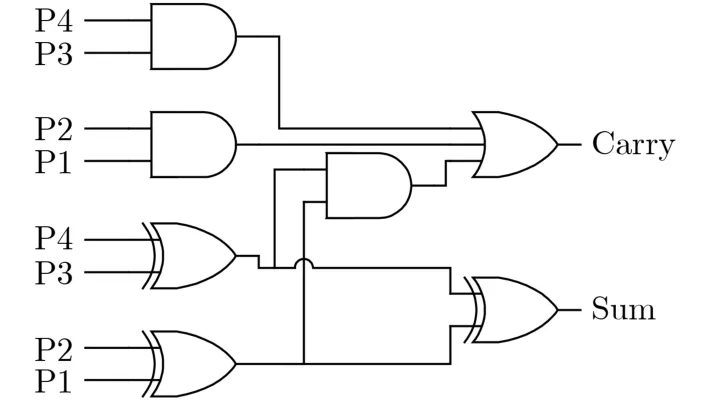
图5 提出的近似4-2压缩器

表3为本文提出的近似4-2 压缩器的真值表，可以看出仅当输入全为1时会产生结果为-2的错误，调整输入顺序不会产生额外错误，即该近似4-2压缩器对输入顺序不敏感。同时，输入全为1的情况出现概率很低，因此该近似4-2压缩器的出错概率小。该近似4-2压缩器的上述特征十分适合输入为1概率不相同且精度要求较高的场景，无需调整输入顺序以降低错误发生概率，直接应用即可。在不引入额外错误的情况下，克服现有近似4-2压缩器不适用于概率分布不均匀的场景，更利于电路的拓展及大规模电路的应用。

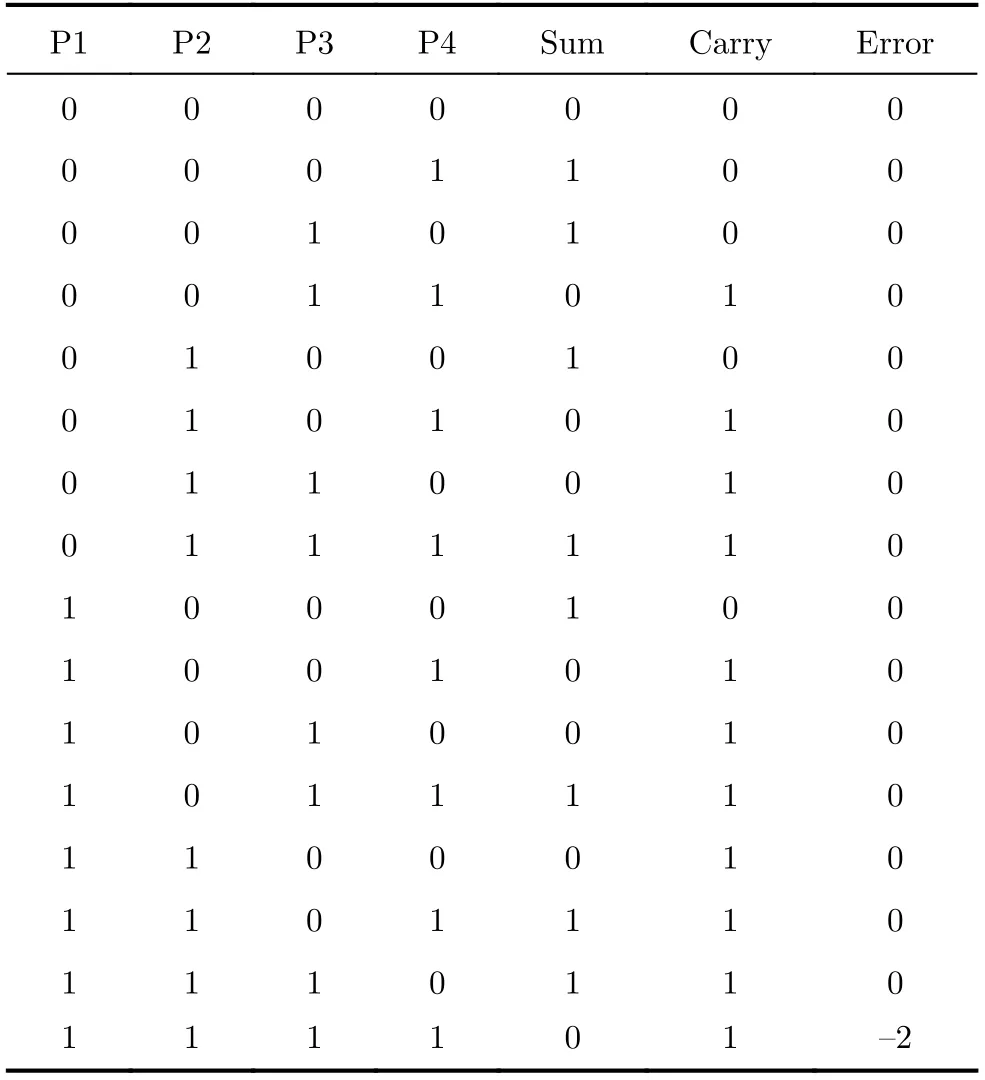
表3 近似 4-2 压缩器真值表

3.3 近似尾数乘法器

本文所提近似尾数乘法器1(Approximate Mantissa Multiplier 1, App-Man-Mul1)对低权重位进行截断并补偿，中间权重位进行近似压缩，高权重位进行精确压缩，具体截断及近似位宽可根据精度要求进行适当调整以达到精度与功耗的平衡。以图6所示的部分积阵列为例，截断低10位部分积(红色虚线框中标识的部分)并在第10位对截断引入的误差进行补偿，同时对第10位到第14位进行近似压缩，其余高位进行精确压缩。

图6 11×11 部分积阵列

或门的真值表如表4所示，该表也给出了在不同的输入情况下对应的错误距离。当或门的2个输入P1,P2全为1，输出结果Out为1，会产生-1的错误距离。当部分积中1的概率不同时，按照概率由低到高，对相同权重的部分积使用或门进行压缩，可大幅度简化压缩结构。因此部分积阵列进行第1级压缩时，对第10,11位的部分积进行如图7所示的基于概率的或门压缩。按照图7压缩时，或门压缩部分产生错误概率最大仅为5.88%，并且错误产生在较低权重位，对最终结果的影响会更小。第12位-第14位无需考虑部分积中1的概率问题使用提出的近似4-2压缩结构，高位使用精确压缩。第1级压缩后，低权重部分积为1概率变大，使用或门压缩引入错误会大幅增加。因此在第2级压缩时，第10,11位使用Ahma近似4-2压缩器，其引入错误较大但结构简单，适用于低位的压缩，其余高位压缩方式与第1级相同。第3级压缩时，在超过两个部分积的第11,12位使用Ahma近似4-2压缩器，剩余部分使用半加器，得到两行部分积。最后在最终求和部分对两行部分积相加产生最终积。

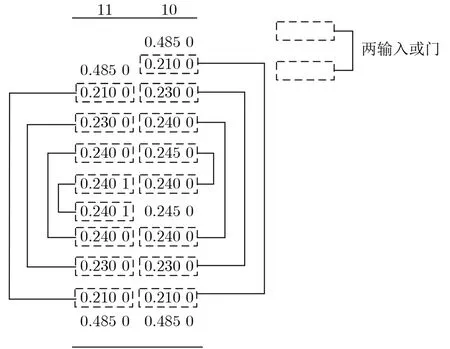
图7 基于概率或门压缩

表4 或门真值表

尾数乘法作为浮点乘法器的关键模块，将图6所示的尾数乘法近似方案应用于浮点乘法中以实现近似浮点乘法器1(Approximate Floating-point Multiplier1, App-Fp-Mul1)。实际应用场景中，可根据精度要求对尾数乘法中的截断位宽、或门压缩使用范围及近似位宽进行适当调整，从而达到精度与硬件指标的平衡。

4 分析与评估

本节通过对比App-Man-Mul1, App-Fp-Mul1和现有近似方案，从误差及硬件指标两方面对设计进行评估。

4.1 误差分析与评估

在近似电路的误差分析中，主要围绕错误距离(Error Distance, ED)对其进行分析。本节使用归一化平均错误距离(Normalize Mean Error Distance, NMED)、平均相对误差距离(Mean Relative Error Distance, MRED)以及均方误差(Mean Square Error, MSE)对近似电路的误差情况进行评估。NMED作为一个关键的评价指标，其值越小表明近似结果与精确结果的差异越小。MRED统计每组输入对应的近似结果与精确结果之间的相对偏差程度，用以更加准确地表示两者的差异。MSE则是从总体上体现误差的波动程度，其值越小说明误差波动越小。各项指标的计算公式在式(2)-式(4)中给出

尾数乘法的近似设计是误差的主要来源，分别对本文提出的App-Man-Mul1及App-Fp-Mul1进行误差评估。使用Matlab平台进行仿真，App-Man-Mul1遍历所有输入情况，App-Fp-Mul1的输入为高斯分布，误差指标如表5和表6所示。相较于通过文献[9-11]中近似压缩器实现的3种近似尾数乘法器 (App-Man-Mul(2-4))以及对应的3种近似浮点乘法器(App-Fp-Mul(2-4))，在NMED, MRED以及MSE 3项精度指标上，App-Man-Mul1降低48%,31%以及55%，App-Fp-Mul1降低58%, 58%以及81%，精度得到显著提升。

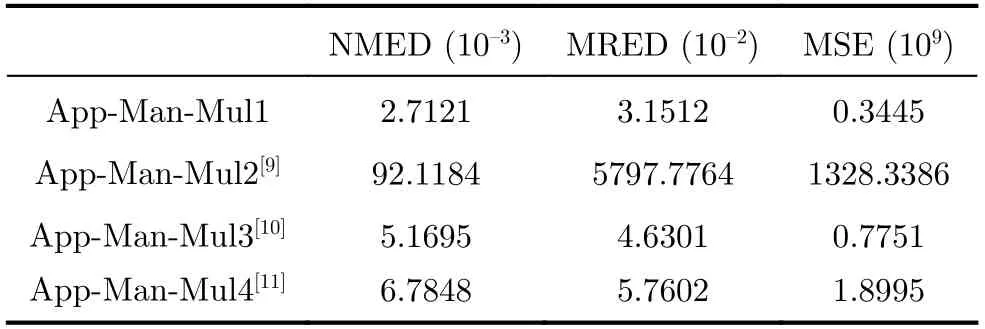
表5 近似尾数乘法器精度指标

表6 近似浮点乘法器精度指标

4.2 硬件分析与评估

使用Verilog HDL语言进行门级电路结构描述，对精确设计、本文提出的近似设计及文献[9-11]的近似设计，首先通过Vivado进行组合逻辑电路的功能验证，然后使用Synopsys公司开发的Design Complier对其在28 nm工艺下进行综合，其中工艺角为SSG，电源电压为0.72 V，环境温度为125 °C。

表7和表8汇总了精确尾数乘法(Exact Mantissa Multiplier, Ex-Man-Mul)、精确浮点乘法器(Exact Floating-point Multiplier, Ex-Fp-Mul)、各近似尾数乘法器及对应的浮点乘法器的面积(Area)、平均功耗(Power)、关键路径延时(Delay)和功耗延时积(Power-Delay Product, PDP)。功耗、面积和延时作为最常用的3个指标，仅从单一指标考虑难以得到最优的结果。引入PDP参数，从功耗延时方面综合考虑设计的整体硬件性能，以便更加合理地评估设计的优劣。

从表7可看出，App-Man-Mul1的PDP仅为Ex-Man-Mul的19%，App-Man -Mul2的72%，App-Man -Mul3的85%，App-Man-Mul4的104%。虽然提出的App-Man-Mul1在PDP指标上略高于App-Man-Mul4，但在App-Man-Mul4设计中同时使用近似4-2压缩和近似6-2压缩，两级压缩后得到最终的两行部分积，占用了较大的面积。从表8看出各浮点乘法器与相应的尾数乘法器的硬件指标规律是一致，这与针对近似浮点乘法器中的尾数乘法部分进行近似设计的思路相符。考虑到浮点乘法器中其他模块的硬件消耗基本相同，近似浮点乘法器的整体的硬件收益比例是会低于近似尾数乘法器，但App-Man-Mul1的PDP仅为Ex-Fp-Mul的42%。

表7 近似乘法器硬件指标(仿真频率500 MHz)

表8 近似浮点乘法器硬件指标(仿真频率200 MHz)

综合考虑误差指标及硬件性能，图8-图10给出了各近似浮点乘法器的PDP与NMED, MRED及MSE的关系。在3组图像中，提出的App-Fp-Mul1的3项指标均位于图像左下角，距离原点最近，即综合最优的近似浮点乘法器设计。

图8 PDP与NMED图

图9 PDP与MRED图

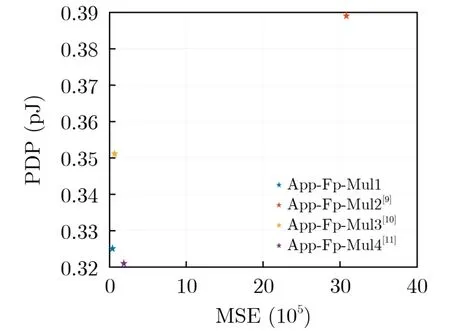
图10 PDP与MSE图

5 HDR图像处理应用

HDR图像具有更广的亮度范围，需使用动态范围较广的浮点数来存储，在进行图像处理时也需要浮点单元来进行实现。因此，将本文提出的近似浮点乘法器应用于HDR图像的图像处理上。具体操作为将两张相同图像的像素点相乘输出到一张图片上，其中的浮点乘法器分别使用精确浮点乘法器以及各近似浮点乘法器。图11(a)-图11(e)分别为使用Ex-Fp-Mul, App-Fp-Mul1, App-Fp-Mul2,App-Fp-Mul3及App-Fp-Mul4的输出，其中两个红框标注的左侧光源及苹果为重点关注部分。

通过Python的图像处理库OpenCV2计算出图像的峰值信噪比(Peak Signal to Noise Ratio,PSNR)与结构相似性(Structural Similarity Index Measure, SSIM)，指标如表9所示。在HDR图像的处理中，综合考虑视觉效果及量化指标，可能会出现明显的视觉差异以及较差的量化指标。例如，人眼能较容易区分出图11(c)-图11(e)与图11(a)，其中图11(d)的视觉效果最差。图11(d)在视觉效果最差的同时PSNR以及SSIM也较低。对比图11(a)与图11(b)，二者视觉效果几乎一致，且图11(b)的PSNR和 SSIM均为近似方案中最高的，进一步说明本文提出的App-Fp-Mul1在图像处理上有良好的应用效果。

图11 图像处理结果

表9 图像处理后的图像的量化指标

6 结束语

本文首先对高斯分布下的半精度浮点数的尾数为1及尾数乘法中部分积为1的概率进行统计分析，得出部分积为1的概率分布规律。基于概率分析提出一种近似4-2压缩器及在低位或门压缩的方法，并给出App-Man-Mul1及App-Fp-Mul1的具体设计。在硬件资源消耗相同或更少的情况下，两种设计在NMED, MRED以及MSE上较现有近似设计都有显著提升，其中App-Fp-Mul1在NMED, MRED以及MSE上至少降低58%, 58%及81%，且PDP仅为Ex-Fp-Mul的42%。在HDR图像的图像处理应用中，App-Fp-Mul1可得到高达83.1638 dB的PSNR及99.9989%的SSIM，App-Fp-Mul1可视为综合最优的近似浮点乘法器设计。但本文工作未对浮点乘法器的其他模块进行简化，仍具备一定改进空间。