改进Langmuir吸附模型建立与电吸附脱盐实验验证
许勇毅,刘 畅,王 峰,马 岚,邢浩若,杨定畅,马双忱
(1.中电华创电力技术研究有限公司,江苏 苏州 215123;2.华北电力大学 环境科学与工程学院,河北 保定 071003)
0 引 言
如今水和能源问题已经成为影响全球可持续发展的两个关键问题。水与能源关系被认为是一个重要的概念,对未来的可持续性规划中具有重要意义。为了提供淡水,多段式闪蒸(MSF),多效蒸馏(MED),反渗透(RO)和电透析(ED)通常用于从苦咸水或海水中除盐。然而,这些技术有一些局限性。如能源效率低下、水电解、膜结垢和产生二次污染。电吸附技术[1,2]是利用带电电极表面吸附水中离子及带电离子的现象,使水中物质在电极表面浓缩富集而实现高效、节能的低盐或中盐水淡化技术,其作为一种高效、节能的水处理技术,具有吸附量大、成本较低、无二次污染、无需加药的优势,在水处理领域前景广阔[3-5]。近年来,关于电吸附在理论、材料、工程应用上都有很多进展,其中理论研究是一切的基础,由最初电吸附理念的提出才有了后续各种材料(如碳纳米管和多孔碳)和工程应用(如电容去离子技术和流动电极电吸附技术)的发展。电吸附模型作为理论发展的重要步骤,其研究不可忽视。
从19世纪末,双电层模型研究就不断深化和发展。目前,大多数CDI实验和模型为恒压充电系统。然而,当系统达到其最低出水浓度时,恒压充电会导致缩短CDI系统的循环时间。这是不希望出现的现象。为了克服这个问题,Jande等[6]脱盐过程选择在恒电流下进行。动态描述了恒流条件下出水浓度随时间变化的响应模型,并对吸附过程进行了推导和验证。此外,还分析了工作电流、流速、CDI装置体积和电容对最低出水浓度的影响。Hemmatifar等[7]开发了一个新的非稳定性二维模型,用于模拟CDI系统中流动的离子吸附/解吸动态、离子的电迁移、扩散和平流之间复杂的、非线性的耦合关系。并验证和校准了这个模型。结果表明,电迁移最终变得可以忽略不计,而扩散性离子迁移降低了脱盐率。Mutha等[8]开发了一个依赖于设备特定参数(系统体积、流量、进水和出水水质)的模型,以概括任何给定需求的单元设计。结果表明,减小对流扩散系数和增加电极的长径比相比通道空间产生最高的盐截留率。通过使用垂直排列碳纳米管电极的实验原型得到验证。这种最大限度地去除盐的框架可以扩展到大量用于CDI设备间流动的多孔电极。Qu等[9]报告了在恒压(CV)和恒流(CC)操作下比较CDI电池的能量消耗的研究。并提出了两种电路模型来模拟充电阶段的能量消耗:一种是简单的电路模型,另一种是传输线电路模型。通过模型和实验得出:在同等充电和充电时间下,CC比CV更节能。模型还表明,充电时的低能耗是由于其较低的电阻耗散所致。Johan等[10]开发并提供了一个开源程序,用户只需进入基本实验条件就可以模拟电容去电离系统的性能。通过预测连续模式恒压运行下的出水浓度如何随时间、流量、施加电压和入口离子浓度等条件变化,证明了该程序的有效性。从而得出动态Langmuir模型可以作为模拟电容去电离动力学的一个有效而简单的工具。然而,要使得电吸附装置的建模和优化更容易实现,作为使研究人员更广泛地获得该技术的手段,还需要做更多的工作。
本文对其进行了总结,介绍了经典的双电层模型(Helmholtz-Perrin、GC、GCS模型),然后进一步讨论现代双电层的发展历程,但目前还没有发展出比较完美的模型。现如今电吸附模型仍在不断地完善中。为此本文给出改进改进Langmuir吸附模型,并利用实验进行了验证。
1 电吸附简介
1.1 电吸附原理
电吸附主要由吸附和脱附两部分构成,原理图如图1所示。当待处理样液通入装置中时,样液中的阴、阳离子在电场力的驱使下分别向阳极和阴极移动,最终被吸附在碳材料上,此过程为吸附过程。值得注意的是,离子所带电荷与电极所带电荷相反,会形成致密双电层EDL[11]。当碳材料吸附至饱和后,需采用倒极的方式,使离子受到相同电荷的斥力,离开碳材料进入预先通入的清水中,形成浓水排出,实现脱附[12,13]。

图1 电吸附与脱附原理示意图Fig.1 Principle of electrosorption and desorption
1.2 电吸附模型
早在19世纪由Helmholtz和Perrin两位学者提出的,用他们的名字命名[14,15]。该模型相当于一个平行板电容器,一侧板上带正电荷,另一侧带有负电荷。Helmholtz-Perrin模型对早期的双电层理论发展有推动作用,但还是存在一定的局限性。该模型没有考虑自身电荷运动问题,仅考虑了反电荷所受的静电力;也没有阐述带电粒子运动时的表面电势与固相和液相电势的差异;并且模型没有涉及到带电离子的水化问题的影响。到了20世纪期,分散层模型(Gouy-Chapman 模型)[16,17]被提出,该模型认为离固相界面的距离与反电荷成反比;距离越大,反电荷越少[18]。分散层的电位与距离固相电极表面的距离呈指数关系变化。GC模型认为热运动和静电力之间是平衡的,没有考虑到固体表面的吸附现象,也具有一定的局限性。为此,Stern在Gouy-Chapman模型进行了进一步的改进,得到了GCS模型[19,20]。该模型不再将扩散粒子看作为点电荷,而将液相电荷以OHP/IHP位置为分界线分为两部分。Stern面内的电荷分布遵循Helmholtz-Perrin模型的规律分布在Stern层外面的电荷遵循Gouy-Chapman模型的规律特点。Stern层与扩散层之间有相对滑动现象,该现象被称为电动现象,滑动面界面处于Stern层与扩散层之间。固体颗粒表面的带电能力可以用滑动面与溶液之间的电势差的大小来表示,该模型对电动现象有了个系统的解释。三种经典模型的对比见表1。

表1 三种经典界面模型对比Tab.1 Comparison of three classical interface models

2 电吸附预测模型建立
电吸附容量是判断电吸附性能的一项重要指标。电吸附装置的吸附容量越大,说明其可以吸附更多的离子,除盐效果也越好。为了提高电吸附容量,具备高比表面积、优良的导电性和化学稳定性等优点的多孔碳成为人们的研究热点,吸附材料通常选用碳材料[21],通常碳材料有:活性炭[22,23]、石墨烯[24],活性炭纤维[25],碳气凝胶[26,27]以及碳纳米管[28]。为深入探究材料及系统的电吸附脱盐性能,本文尝试建立预测电吸附容量模型。针对CDI阳极,通过将TiO2与CNTs复合作为其吸附材料,提高电吸附性能,除去脱硫废水中的氯离子。
2.1 吸附量计算
1916年,美国科学家Langmuir根据气体分子在固体表面被吸附的现象,提出了著名的Langmuir等温方程式[29]。如今,Langmuir方程也已经从气体吸附推广到了固液吸附,并应用在了多个领域。本实验建立的模型是基于经典Langmuir等温方程的基础之上,根据实验的实际情况而改进的电吸附吸附量模型。
对于经典的Langmuir方程,其假设是气体发生吸附,并且是在纯净的固体上,气体可直接与作为吸附剂的固体表面的空白点位结合,平衡式如下:
S(表面)+A(气体)⟺A-S
(4)
(5)
式中:θ为覆盖率;p为气体的压力,Pa;kad为吸附和脱附的平衡常数,等于吸附速率常数比解吸速率常数的数值,Pa-1。
将相关假设运用在固液吸附过程中:
S(表面)+A(溶液)⟺A-S
(6)
单位面积的吸附剂对吸附质的吸附速率和两个因素成正比,分别是吸附质浓度还有吸附剂表面空白吸附点位比例,公式如下所示:
ra=kaC(1-θ)
(7)
式中:ra为吸附速率,mol L-1s-1;C为吸附质浓度,mol L-1;ka为吸附速率常数,mol L-1s-1。
吸附质在吸附剂表面的解吸速率与吸附剂表面覆盖率θ成正比,因此可得
rd=kdθ
(8)
式中:rd为解吸速率,mol L-1s-1;kd为解吸速率常数,mol L-1s-1。
这一过程经过一段时间后会达到平衡,此时吸附速率与解吸速率相等,即
kaC(1-θ)=kdθ
(9)
整理得
(10)
又因为
(11)

(12)
在本实验中,为了计算更加方便,将吸附摩尔量转化为吸附质量,最终得出改进Langmuir方程:
(13)
式中:m为吸附质量,mg.g-1;mmax为饱和吸附质量,mg·g-1。
2.2 CDI脱盐实验
为了更好地说明实验与模型之间的关联性,本文分别从实验与模型两部分进行了分析讨论。实验分为两个部分:第一部分,在电压为0.4 V、0.8 V、1.2 V以及1.5 V的条件下,以NaCl溶液为样液,探究不同电压下除氯效果。第二部分,在电压为1.2 V,初始浓度为100mg/L,流速为50mL/min的条件下,对比了纯CNTs以及TiO2与CNTs的复合材料(TiO2所占比例分别为15%、30%、60%,记作:15%T/C、30%T/C、60%T/C)的除氯能力。采用循环进样的方式对200mL的NaCl溶液进行处理。
对于本实验,随溶质浓度变化,不同比例吸附材料(纯CNTs、15%T/C、30%T/C和60%T/C)对氯离子的吸附量模型;随溶质浓度变化,不同电压下吸附材料对氯离子的吸附量模型。最大电吸附容量(EC,mg/g)可通过以下等式计算:
(14)
式中:C0为NaCl溶液的初始浓度,mg/L;CE为NaCl溶液的平衡浓度,mg/L;V为NaCl溶液的总体积,L;m为电极材料总质量,g。
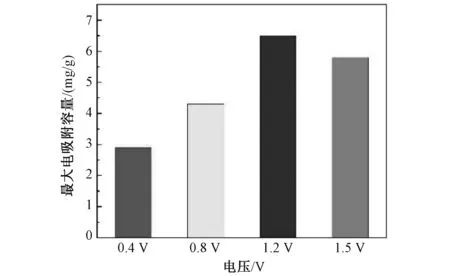
图2 不同电压下的最大吸附量Fig.2 Maximum adsorption capacity at different voltages
由公式(14)计算得到在不同的操作电压下(0.4 V、0.8 V、1.2 V以及1.5 V),60%T/C的最大吸附量分别为:2.9mg/g、4.3mg/g、6.5mg/g、5.8mg/g。在电压为1.2 V时,60%T/C复合材料具有最大的吸附容量;其次再是1.5 V的电压所对应的60%T/C复合材料的吸附容量,0.4V电压下,60%T/C复合材料拥有最低的吸附容量。通过该实验可以得出,随着电压的增加,吸附容量逐渐增大,这表明电场力的迁移作用起到主导作用,且远大于物理吸附。

图3 不同比例的TiO2/CNTs复合材料的最大吸附容量Fig.3 Maximum adsorption capacity of TiO2/CNTs composites with different ratios
由公式(14)计算得到纯CNTs、15%T/C、30%T/C和60%T/C的最大吸附量分别为:5.06mg/g、5.06mg/g、6.35mg/g、6.5mg/g。60%T/C具有最大的吸附容量,30%T/C与60%T/C的复合材料的吸附容量相差不大,但仍稍逊于60%T/C。因此,可以总结随着TiO2比例的增加,氯离子的去除效果明显上升。综上,60%T/C是最佳的复合材料比例。
2.3 CDI吸附模型
将2.2节实验所得数据带入到2.1节所得出的改进Langmuir模型中,利用Matlab软件进行拟合。最终,得到电吸附装置吸附氯离子的吸附量模型。图4为NaCl浓度从0~2g/L变化时,不同电压下60%T/C复合材料吸附容量ma。由图4中可以得到:在电压为1.2 V时,60%T/C复合材料具有最大的吸附容量;其次再是1.5 V的电压所对应的吸附容量,0.4 V电压下复合材料拥有最低的吸附容量。图5为NaCl浓度从0~2g/L变化时,不同比例的TiO2/CNTs复合材料的吸附容量m1。从图5中可以看出,60%T/C具有最大的吸附容量,30%T/C与60%T/C的复合材料的吸附容量相差不大,但仍稍逊于60%T/C;15%T/C的复合材料和纯的CNTs材料曲线重合,说明它们的吸附能力接近。结合图4和图5可以看出,改进Langmuir模型所模拟出的趋势和实验所得结论一致。
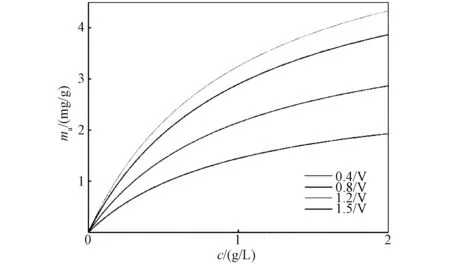
图4 不同电压下60%T/C复合材料的吸附容量模拟图Fig.4 Simulation of adsorption capacity of 60% T/C composite at different voltages

图5 不同比例的TiO2/CNTs复合材料的吸附容量模拟图Fig.5 Simulation of adsorption capacity of TiO2/CNTs composites with different ratios
3 影响因素分析
前述吸附容量模型理论推导,理论上吸附的溶液层是无限延伸的,但实际具有一定的厚度,只有在这一厚度下的离子才能够被电极板吸附。在实际运算中,实际吸附容量小于理论值,因为有吸附材料孔道、系统电阻等因素的影响。如图6所示,在d1的范围内,离子才能被电极板吸附。

图6 电荷的分布与距离的关系Fig.6 Distribution of charge versus distance
其次,TiO2/CNTs复合材料内的孔径大小肯定不是均匀一致的,并且内部孔道是曲折的。复合材料和孔道内的溶液都有一定的电阻,并且在将吸附材料涂覆在电极板上时,需要加入粘结剂,电阻会加大。电极的切面图可由图7表示。

图7 电吸附装置的剖面图Fig.7 Cross-sectional view of the electro-sorption device
3.1 孔径对复合材料吸附量的影响
电场力的作用外加离子热运动,离子会分布在距离为d的范围内,d的大小为
d=εrS/4πkC
(15)
式中:εr是相对介电常数;S为电容极板的正对面积;k则是静电力常量;C为电容。
将TiO2/CNTs复合材料看作由许多大小不一的孔道组成,则此时d相当于孔半径,只有一部分离子能进入双电层,另一部分离子因为半径比孔径大,被截留在孔道外部。所以实际情况下电吸附量与理论计算值不同。
3.2 孔隙率对复合材料吸附量的影响
若孔的深度为L,孔道半径为r,孔数量为n,孔道的表面积S可由式(16)表示:
S=2πnrL
(16)
从公式(16)中可以看出,孔道半径越小,比表面积越大,吸附的效率也更高,但当孔半径减小到一定程度,越来越少的离子能进入孔内,所以材料孔隙的大小对电吸附容量也有影响。所以,实际测出的电吸附量M0小于经验公式算出的M值。
4 讨 论
电吸附建模的最终目的是导出一个数学公式,该公式不仅能描述先前记录的数据,而且可以预测CDI在各个方面的性能,包括脱盐程度、pH波动、能耗等。这种设计模型应该能够在电极结构的输入参数(厚度、孔隙率)、电池设计和外部条件(如开关时间、外加电流和电压信号等)的广泛范围内实现[30]。同时,设计模型可以与包含能源和材料价格的成本计算模块相结合,一起进入成本优化公式,以计算精确定义应用程序的最佳CDI电池设计和操作模式。然后,可以将该最优值与其他水处理技术的各自最优值进行比较。
这一目标目前仍远远不能实现,但CDI系统在设计模型的最终开发方面已经走了相当长的一段距离,该设计模型能够预测所有可能的数据集(例如,包括/不包括膜;恒压与恒流)的性能,所有模型参数均为定值。鉴于CDI电池的许多元素尚未被包括在内,例如质子/羟基离子的影响、化学表面电荷和氧化还原功能,这是一个重大的挑战。因此,未来CDI模型的挑战是预测带电多孔介质和双电层结构中离子输运的电动力学。
随着改进的双电层结构模型的发展,双电层结构模型必须足够简单,易于集成到多孔电极传输模型中,这一点也很重要。此外,当将模型扩展到环境应用中典型的离子混合情况时,它们在数学上应该保持理想的简洁性。此外,离子可能发生酸碱平衡反应是能实现的。
5 结 论
本文建立了改进Langmuir吸附量模型电吸附脱盐吸附量预测模型,主要结论如下:
(1)通过建立不同比例吸附材料对氯离子的改进Langmuir吸附量模型,结果显示:纯CNTs、15%T/C、30%T/C和60%T/C的最大吸附量分别为:5.06mg/g、5.06mg/g、6.35mg/g、6.5mg/g。并通过实验验证60%T/C复合材料具有最大的吸附容量。
(2)通过建立不同电压下60%T/C吸附材料对氯离子的改进Langmuir吸附量模型,并通过实验验证,由计算得到在不同的操作电压下(0.4V、0.8V、1.2V以及1.5V),60%T/C的最大吸附量分别为:2.9mg/g、4.3mg/g、6.5mg/g、5.8mg/g。因此,在电压1.2V时,60%TiO2/CNTs复合材料拥有最大吸附容量;0.4V电压下60%TiO2/CNTs复合材料拥有最小吸附容量;
(3)根据改进Langmuir吸附量模型,本文对于孔径和孔隙率对吸附率的影响进行了分析。并在最后指出CDI模型仍然面临着很多改进,未来的研究将会更多偏向于预测带电多孔介质和双电层结构中离子输运的电动力学。

