基于组合赋权和TOPSIS的配电网CPS系统脆弱性评估
谷卫星,王婷婷,张 鹏,苏 宁,王 玥,汤 奕,于红丽,刘毅梅,龚钢军
(1.北京电力经济技术研究院有限公司,北京 100055;2.北京市能源电力信息安全工程技术研究中心(华北电力大学),北京 102206)
0 引 言
随着先进传感检测技术、智能控制技术、新一代信息通信技术及高效数据处理技术在配电网的推广应用[1],配电网的运行效率及智能自动化水平大幅提高,现代配电网已经逐渐衍生为一个融含通信网络、物理系统、控制与计算系统的信息物理系统[2]。与此同时,配电系统与信息系统的耦合程度也逐渐加深,新一代信息通信技术在给系统带来便利的同时,也加深了配电网信息物理系统(以下简称:配电网CPS)安全风险[3],轻则导致部分用户停电,重则导致级联故障的发生,影响到大电网的安全稳定运行[4]。因此,有效辨识配电网CPS系统的薄弱环节并对其进行量化评估已迫在眉睫。
目前,分析配电网脆弱性的方法主要聚焦于分析配电网的结构脆弱性与状态脆弱性。文献[18]提出电网脆弱性指数、供电效率值等指标来评价含集成式DG电网的结构脆弱性;文献[19]基于复杂网络模型,将节点差异性、边差异性、结构熵值作为衡量系统脆弱性的指标;文献[22]采用节点电压脆弱度、支路潮流脆弱度指标表征通信故障时主动配电网系统的状态脆弱性;文献[23]将DB攻击策略下系统节点的存活率作为系统的脆弱性评估度量值。以上文献在评估系统的脆弱性时,均局限于单一电力网络。配电网CPS系统作为典型的双侧网络复杂系统,其系统的脆弱性同时受到单侧网络与网间依存关系的影响。
因此,本文首先基于相依网络理论及配电网拓扑结构特点建立了配电网相依网络模型,为综合分析配电网CPS双侧空间的脆弱性,基于配电网实际通信业务与特殊拓扑结构特点建立了评价指标融合模型;并结合最小鉴别信息原理完成对指标主客观权重的综合度量,最后采用TOPSIS算法对节点的脆弱度进行量化排序,基于依存耦合度矩阵实现对两侧节点脆弱度的综合评估。
1 配电网CPS系统耦合网络建模
配电网CPS系统是一次配电网和信息系统(配电自动化系统及其信息通信网络)深度融合的二元耦合系统。为了表征系统信息与物理环节交互影响及耦合机理,本文采用“部分一对一相依网络”模型对系统进行耦合建模[9],具体如图1所示。由于配电网CPS系统在设备类型、数量、部署方式等方面存在较大差异[10],为简化处理,本文假设如下:
(1)物理节点。配电网一次系统中的分布式电源、配电变压器、负荷等抽象为一个电力物理节点,为突出其重要性,本文将其等效为电源节点。
(2)信息节点。在配电网实际运行过程中,需要对其实时状态信息进行采集、监视与控制,且为了保证物理节点可以动态地接受配电主站下发的控制命令,通常会在相关物理节点旁边配备相关的二次设备节点。
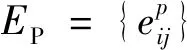
其次,通过定义依存边集合ED来表征配电网信息侧与物理侧节点之间的相互依存关系,即ED={EC-P,EP-C},EC-P表征信息节点对电力节点的依存边矩阵,EC-P(x,y)=1表示信息节点x的正常运行需要物理节点y的电力供应,否则,EC-P(x,y)=0;EP-C表征电力节点对信息节点的依存边矩阵,EP-C(y,x)=1表示物理节点y的正常运行需要信息节点x的安全控制,否则,EP-C(y,x)=0。因此,配电网信息-物理相依网络模型可以表示为G=(GP,GC,ED)。
2 考虑配电网信息-物理两侧节点脆弱性分析
配电网CPS系统作为配电网智能化生产与信息化管理的基础,影响其节点脆弱性的因素较多,就信息侧而言,不同节点的重要性不同;就物理侧而言,不同节点脆弱性相差较大。因此,为评估系统网架的脆弱性,亟需从信息、物理两个层面分析系统节点的脆弱度,建立了如图1节点脆弱性评价指标模型分析配电网CPS的脆弱性。

图1 节点脆弱性评价多指标融合模型Fig.1 Multi-index fusion model for node vulnerability evaluation
图1中节点脆弱度需综合考虑“准则层”所包含的信息侧与物理侧两方面内容,各指标代表的具体含义见下文。其分析与计算过程如下:1)计算指标层各指标点的脆弱度值;2)根据综合权重求解方法,计算出同一准则层下各指标项的权重,并利用TOPSIS算法求得准则项各个节点方案的脆弱度值,且将信息侧与物理侧各节点方案的脆弱度值进行排序;3)依据配电网信息-物理相依网络模型中两侧节点的依存耦合度矩阵,确定配电网CPS系统中节点的综合脆弱度值,完成对系统的脆弱性量化评估。
2.1 计及信息侧节点脆弱度分析
配电网CPS系统的信息通信网络,是实现配电网各类自动化与智能化业务的关键所在,信息流的可靠传输也是保证配电网安全、稳定、可靠运行的重要条件,且当信息通信网络遭受内部元件损坏或外部人为破坏的情况下,势必通过信息-物理的跨空间传播机制影响到配电网的一次运行,导致重要用户断电、孤岛电网产生等安全事故。因此,为完成对配电网CPS系统的脆弱性评估,有必要分析配电网CPS系统信息侧节点的脆弱性,为将来提供针对性的安全防护措施奠定基础。
配电网作为智能电网的神经末梢,为电力终端用户提供了各种各样的安全可靠性业务,而相应业务的成功实施必然依托于配电网信息侧节点的安全稳定运行。因此,为完成信息侧节点的脆弱度评估,本文主要基于相关配电通信业务构造信息侧节点的脆弱度指标,具体包括“遥测”、“遥信”、“遥控”、“遥视”四类业务[11],如表1所示。

表1 信息侧节点指标项详细信息分布Tab.1 Detailed information distribution of node indicators on the information side
文中表1列出了配电网信息通信业务的详细信息,据表可知配电网CPS系统相应业务根据不同的分类方法加以区分,①按照业务功能来分,包括“遥测”、“遥信”、“遥控”、“遥视”等四种电力生产与管理业务;②按照业务数据类型,可分为语音业务、数据业务及视频业务,在配电信息通信业务中主要以数据类业务为主,视频类业务为辅,极少数有语音业务;③按照通信实时性来分,包括实时性业务与非实时性业务,不同业务的通信传输时延也不太一样;④按照业务流向来分,包括上行业务(如遥测、遥信等)与下行业务(如遥控等);⑤按照通信传输的可靠性可分为高、中、低可靠性业务,主要是通过丢包率的高低来衡量,且丢包率越高,可靠性越低。
2.2 计及物理侧节点脆弱度分析
为完成对配电网CPS系统物理侧节点脆弱性的分析与评价,本节借鉴复杂网络理论提出相关评价指标并做出相关改进,以此完成对系统物理侧节点脆弱性的研究。传统意义上的复杂网络通过提出度数、介数、平均路径长度等具有统计特性的指标来反应系统结构的分布规律[12],进而实现对系统结构脆弱性的分析,能够在输电网的脆弱性评估中得到广泛应用[13]。但相比于输电网,实际配电网有其自身的一些结构特点与运行规律,主要包括:(1)配电网的拓扑结构相比于输电网更加稀疏,且多为辐射状;(2)目前大部分文献在对输电网进行脆弱性分析时,多采用某节点移除后系统的失负荷量等指标来衡量系统的脆弱性,由于配电网结构更为稀疏,若单电源的配电网系统在电源节点移除后将会导致全文崩溃,所以传统意义上的输电网脆弱性分析方法不再适用;(3)配电网中的动态元件相比于输电网较少,需用静态的角度建立节点脆弱性评价指标模型。因此,本文对相关指标进行改进,具体如下。
(1)改进节点度数。传统节点度数定位为与某节点相连的边数,用来表征其在局部网络中的重要性[14],且重要性的大小与该数值的大小程度呈正相关,在对输电网进行结构脆弱性评估时,该指标具有较好的适用性。但在网架结构更为稀疏的配电网中,传统意义上的节点度数无法反映具有相同度数节点之间的差异性。因此,需综合考虑该节点与相邻节点的度数,以反映节点之间的差异性。本文提出改进节点度数DNi为
(1)
式中:Di为节点i度数与其相邻节点度数之和N为节点总数。
(2)
式中:di为节点i的度数;Oi表示与节点i相邻节点的集合。
(2)改进节点介数。传统节点介数为网络中经过某节点的最短路径数目,用来表征其在整个网站运行控制的重要性[15],且重要性的大小与该数值的大小呈正相关,可以较好地描述节点在全局的统计特性,可以较好地适配于输电网的结构脆弱性评估。但是配电网大多数为辐射状开环运行状态,传统意义上的节点介数无法反映配电网潮流分布情况。因此,本文考虑到实际配电网潮流流动方向,根据节点传输功率的作用大小,提出新的节点介数BNi为
(3)
式中:k为节点总数;m为等效电源节点;n为负荷节点;G为电源节点集合;n为负荷节点集合;λmn为节点m、n之间最短路径数量;λmn(i)为λmn中经过节点i的数量;n为负荷节点,F为负荷节点集合。
(3)改进节点紧密度。传统节点紧密度指标可以反映某节点与其他节点连接的紧密程度[16],仅从全局的角度评价节点的重要度,却忽略了节点的局部信息。因此,考虑到节点在配电网中的全局以及局部重要性,提出新的节点紧密度CNi为
(4)
(5)

(4)节点注入功率比。为了衡量不同节点在配电网能量流传输分配过程中的重要性,本文引入节点注入功率比的概念来表示[17]。该值越大,代表该节点在配电网中传输的功率越多,一旦发生故障,对配电网的影响程度越大,导致脆弱性就越高。节点注入功率比μNi的计算公式为
(6)
式中:Pi为节点i的注入功率;Sbase为系统的基准容量。
3 基于组合赋权和TOPSIS算法的配电网CPS节点脆弱性量化评估方法
为完成对配电网CPS系统节点脆弱性的量化评估,有必要将系统的节点脆弱度进行综合排序,以便找出系统中脆弱度最高的节点。基于此,本文分别将信息侧与物理侧的节点作为一个备选方案,将表征配电网业务属性与拓扑结构的具体指标作为系统脆弱性的评判属性,从而将系统节点的脆弱性评估转化为一个多属性决策问题[18],本文采用TOPSIS算法与主客观综合赋权的方法对该问题进行解决。TOPSIS算法可以从备选方案和理想方案的距离对备选方案进行脆弱性评估并排序[19],分别可以得到信息侧和物理侧两侧节点的脆弱度排序,并基于两侧节点的依存耦合度矩阵实现对配电网CPS系统脆弱性的综合评估。
3.1 基于最小鉴别信息原理的指标综合赋权方法
本文在权重确定方面,分别采用模糊层次分析法和熵值法对指标项aj的主客观权重进行计算,并基于最小鉴别信息原理实现对指标的综合赋权。
模糊层次分析法是一种将模糊数学的概念应用于层次分析法中的主观权重决策的方法,较好地体现了各个指标之间普遍存在的模糊性与不确定性,间接地消除了一致性问题[20]。具体计算步骤为
1)通过对比同一准则层下各个指标的重要程度构建模糊互补判断矩阵,具体为
(7)
式中:bij为0.1~0.9之间的小数,表示指标项ai相比于指标项aj的重要程度,值越大代表指标项aj越重要,且满足bij+bji=1。
2)将B变换为模糊一致判断矩阵Bf=(fij)n×n元素fij计算公式为
(8)
式中:bi为矩阵B中第i行元素之和。
3)根据矩阵Bf=(fij)n×n计算各个指标的权重值。同一准则层下第i个脆弱性指标的主观权重值ωzi为
(9)
式中:α为参数,满足α≥(m-1)/2,α的大小与权重的差异度呈反比。本文取α=(m-1)/2。
熵值法是一种客观的权重赋值法,是根据各指标观测值所代表的信息量大小进行权重确定[21]。具体计算步骤为
1)构建评价数据矩阵:设有m个评价项,n项评级指标,则原始指标矩阵为
(10)
2)指标归一化处理。
(11)
3)计算第j项指标的熵值ej和冗余程度hj。
(12)
式中:k>0,ln为自然对数,常数k与参与脆弱性评价指标总数n有关,一般取值为k=1/(lnn)。
hj=1-ej
(13)
其中,第j项指标的冗余度hj越大,则指标对方案的评价作用越大。
4)计算同一准则层下第i个脆弱性指标的客观权重值ωki为
(14)
由上述模糊层次分析法和熵值法分别可以计算出主客观权重向量ωz={ωz1,ωz2,…,ωzn}T、ωk={ωk1,ωk2,…,ωkn}T,本文采用最小鉴别信息原理实现对主客观权重的融合[22],进而求得各指标项的综合权重向量ω=[ω1,ω2,…,ωm]T。具体计算步骤为
1)基于最小鉴别信息原理设定目标函数:
(15)
2)基于拉格朗日函数对目标函数进行求解。
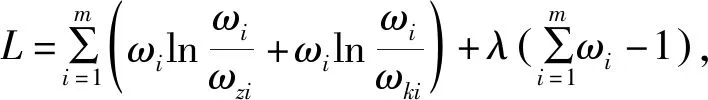
(16)
因此,可得综合权重ωi为
(17)
因此各指标项的综合权重向量为ω=[ω1,ω2,…,ωm]T。
3.2 基于组合赋权和TOPSIS算法的节点综合脆弱性计算
基于组合赋权和TOPSIS算法[23]的配电网CPS系统节点脆弱度评价流程如图2所示。具体计算过程为

图2 基于组合赋权和TOPSIS算法的节点脆弱度评价流程Fig.2 Node vulnerability evaluation process based on combined weighting and TOPSIS algorithm
1)基于配电网CPS系统业务特征及拓扑结构模型,建立节点脆弱度评价指标模型。
2)建立准则层的规范化矩阵ZV=(zij)n×m。
(18)
式中:zij为准则层Vk下第i个节点的第j项细化指标的数值(如节点度数、节点介数等),m为信息侧或物理侧的节点总数,n为准则层Vk下细化指标个数。由于不同指标之间的单位类型及数量级大小不同,为保证各个指标之间的对比更具合理性,本文对各个指标进行归一化处理得到归一化规范矩阵TV=(tij)n×m,具体归一化计算公式为式(19)、(20),确保取值为区间[α,1],本文中α取值为0.1。
效益型指标:指标值越大越好。
(19)
成本型指标:指标值越小越小。
(20)
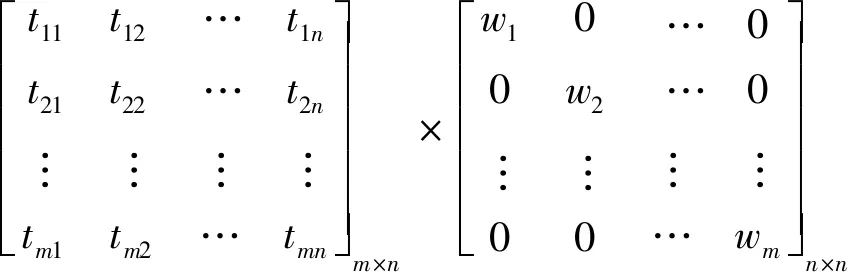
3)基于前文计算出的综合权重向量ω,计算加权规范化矩阵GV,为
GV=(gij)m×n=
4)在矩阵GV中,分别将每个指标下节点的最大值、最小值作为系统的正、负理想解,进而计算相对贴近度,具体计算过程为
设正理想解为
负理想解为
式中:L={1,2,…,m}。
(22)
(23)
从而可以得到第i个节点的第V项指标的贴近度βVi为
(24)
正理想解体现了信息侧或物理侧节点可能存在的脆弱度最大值,贴近度可以反映信息侧或物理侧节点的脆弱度与正理想解的相近程度,且贴近度值与节点脆弱度值呈正相关。因此,该方法可以分别计算信息侧与物理侧节点的脆弱度值,并且基于节点依存耦合度矩阵可以得到配电网CPS系统的节点脆弱度值。由于两侧节点之间依存强度并不是简单的0、1关系,而与实际配电网CPS系统的运行特点与业务特征有关,本文分别对依存耦合度矩阵Fc-p、Fp-c进行定义,具体为
(25)
式中:Fc-p(i,j)为信息网节点i与物理网节点j的依存耦合度值,表征了节点i对节点j的影响程度,具体含义为与该电力节点j相依的信息网节点i因为电力网节点运行而产生的实际通信业务量值hij占全网通信业务总量Htotal的比值。不同节点之间的依存耦合度值Fc-p(i,j)(i=1,2,…,m;j=1,2,…n)构成了依存耦合度矩阵Fc-p。
(26)
式中:Fp-c(i,j)为物理网节点i与信息网节点j的依存耦合度值,表征节点i对节点j的影响程度,具体含义为与该信息网节点j相依的电力网节点i因为信息网节点运行而消耗的实际功率值占全网功率总量Ptotal的比值。不同节点之间的依存耦合度值Fc-p(i,j)(i=1,2,…,n;j=1,2,…m)构成了依存耦合度矩阵Fp-c。
根据配电网CPS系统双侧节点的脆弱度值及依存耦合度矩阵,可以计算出信息物理耦合视角下,考虑依存边影响程度的配电网节点i综合脆弱度值。见式(27)和(28)。
(27)
式中:VCPS-P为信息物理耦合视角下,考虑相依边影响程度的配电网节点i脆弱度;VP(i)为仅考虑物理侧节点i脆弱度值;VC(j)为仅考虑信息侧节点j脆弱度值。
(28)
式中:VCPS-C为信息物理耦合视角下,考虑相依边影响程度的配电通信网节点i脆弱度;VC(i)为仅考虑信息侧节点i脆弱度值;VP(j)为仅考虑物理侧节点j为仅考虑物理侧节点i脆弱度值脆弱度值。
4 算例分析与验证
为验证所提评估方法的有效性,本文以IEEE14节点配电系统为物理侧拓扑结构,该配电网包括14个节点,3条馈线,系统基准容量与电压分别为100 MVA、23 kV[24];根据配电网CPS系统信息侧与物理侧节点的“部分一对一”耦合关系,建立信息拓扑结构模型,具体如图3所示。其中,物理网中编号为1的节点与上级电网相连,等效为电源节点;信息网中编号为15的节点为配电主站节点,等效为“自治节点”。
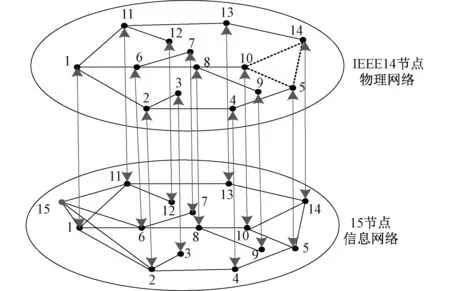
图3 配电网CPS验证算例Fig.3 Calculation example of CPS verification for distribution network
(1)信息侧节点脆弱度计算
对于配电网CPS系统信息侧节点的脆弱度,由于不同信息节点承担的业务类型与业务数量可能存在较大差异,且为满足信息侧节点的业务需求,设置各个信息节点具体业务指标值如附表1。
通过分析配电网具体业务类型,将不同业务下的各个指标aj={a1,a2,a3,a4,a5}={数据类型,节点处理时延,实时性,数据量,丢包率}的重要度进行对比,建立模糊互补矩阵B,利用FAHP求得各个指标的主观权重向量ωzj={ωz1,ωz2,ωz3,ωz4,ωz5}={0.2,0.225,0.225,0.15,0.25}。
由于各个业务的数据类型指标为定性指标,根据等级评分标准进行赋值。通过建立各个指标aj的原始矩阵,根据熵值法求得指标客观权重向量为ωkj={ωk1,ωk2,ωk3,ωk4,ωk5}={0.124 6,0.140 3,0.119 6,0.321 1,0.294 4}根据最小鉴别信息原理求得综合权重向量为ωj={ω1,ω2,ω3,ω4,ω5}={0.159 4,0.179 4,0.165 7,0.221 6,0.273 9}。
因此,基于信息侧各个细化指标的数值及权重向量,并采用本文基于组合赋权和TOPSIS算法的节点脆弱性计算方法计算各个节点的脆弱度,最后在Python3.7版本进行模拟仿真,得到信息侧节点得脆弱度值(见表2)。

表2 信息侧节点脆弱度值(取小数点后四位)Tab.2 Vulnerability value of information side node(take four digits after the decimal point)
(2)物理侧节点脆弱度计算
为计算配电网CPS系统物理侧节点的脆弱度,根据上文定义的改进节点度数、改进节点介数、改进节点紧密度、注入功率比等细化指标对IEEE14节点模型进行量化计算,其各个节点的指标量化值见表3。

表3 物理侧节点脆弱度值(取小数点后四位)Tab.3 Vulnerability value of physical side node(take four digits after the decimal point)
根据配电网CPS系统物理侧节点各个评价指标的具体含义,对比各个指标aj={a1,a2,a3,a4}={改进节点度数,改进节点介数,改进节点紧密度,注入功率比}的重要程度,建立模糊互补矩阵B,通过FAHP计算各个指标的主观权重值为ωzj={ωz1,ωz2,ωz3,ωz4}={0.2,0.233,0.3,0.267}。
通过建立各个指标aj的原始矩阵,根据熵值法求得客观指标权重向量为ωkj={ωk1,ωk2,ωk3,ωk4}={0.234 8,0.370 9,0.217 3,0.177 0}。根据最小鉴别信息原理求得综合权重向量为ωj={ω1,ω2,ω3,ω4}={0.220 4,0.298 9,0.259 6,0.221 1}。
因此,基于物理侧各个细化指标的数值及权重向量,并采用本文基于组合赋权和TOPSIS算法的节点脆弱性计算方法计算各个节点的脆弱度,最后在Python3.7版本进行模拟仿真,得到各个节点得脆弱度值(见表4)。
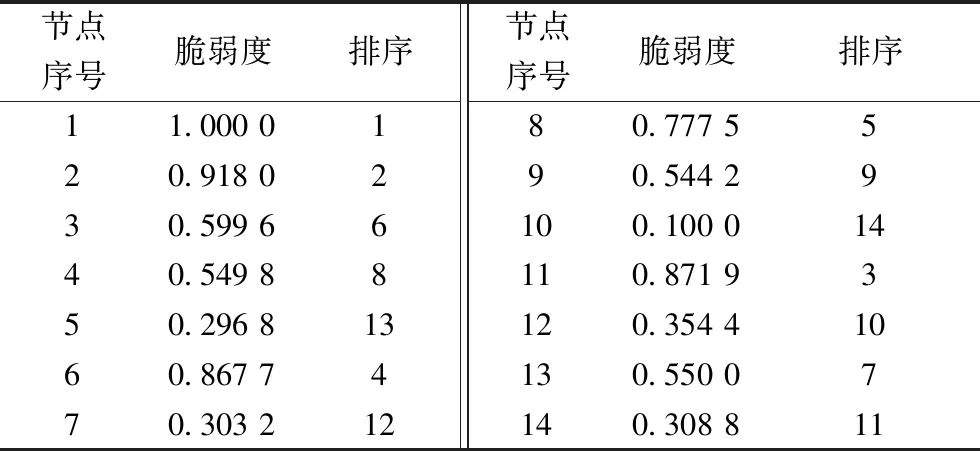
表4 物理侧节点脆弱度值(取小数点后四位)Tab.4 Vulnerability value of physical side node(take four digits after the decimal point)
(3)相依网络理论下配电网CPS系统节点脆弱度计算
配电网CPS系统是物理空间与信息空间相互影响的复杂电力系统,为综合衡量系统节点的脆弱性大小,需考虑两侧网络节点的相互依存程度,可以分别建立网间依存关系耦合度矩阵Fp-c(i,j)、Fc-p(i,j),根据本节配电网CPS系统仿真算例模型,其耦合度矩阵见附录。
根据配电网CPS系统物理网与信息网单侧节点的脆弱度值,分别将依存耦合度矩阵作为两侧网络之间的映射函数,利用式(27)、(28)得到相依网络理论下的信息物理耦合节点的综合脆弱度值,见表5、6。
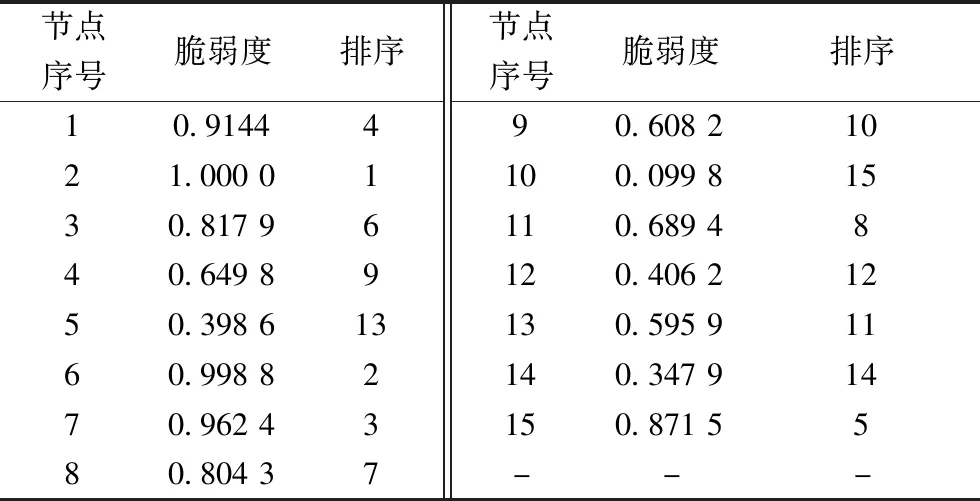
表5 考虑配电网CPS耦合特性的信息侧节点脆弱度值(取小数点后四位)Tab.5 Vulnerability value of information side nodes considering the coupling characteristics of CPS in distribution network(take four digits after the decimal point)
以信息网节点1、2为例,在单侧信息网络中,节点的脆弱度值都为0.992 3,是因为两个节点承担的业务类型相同,都包括“遥测”、“遥测”、“遥控”、“遥视”四种业务类型,而在考虑相互依存关系后,节点脆弱度变为0.914 4和1.000 0,表明在单侧网络节点脆弱度相同的情况下,耦合网络会对其脆弱度指标产生影响,脆弱度值排序结果也由并列第2位变为第4、1位;以信息网节点10为例,耦合网络对其的影响程度为0.091 0,在单侧信息网中节点的脆弱度为0.100 0,为单侧网络中节点脆弱度值的最小值,在考虑耦合网络的影响值之后,节点的脆弱度变为0.099 8,依然为最小值,表明在评价信息网节点的脆弱度值时,纵使考虑相依网络的影响,单侧网络本征脆弱度值仍起着关键作用。将单侧信息网节点脆弱度值与考虑耦合网络依存度的影响的节点脆弱度值进行对比,结果如图4所示。
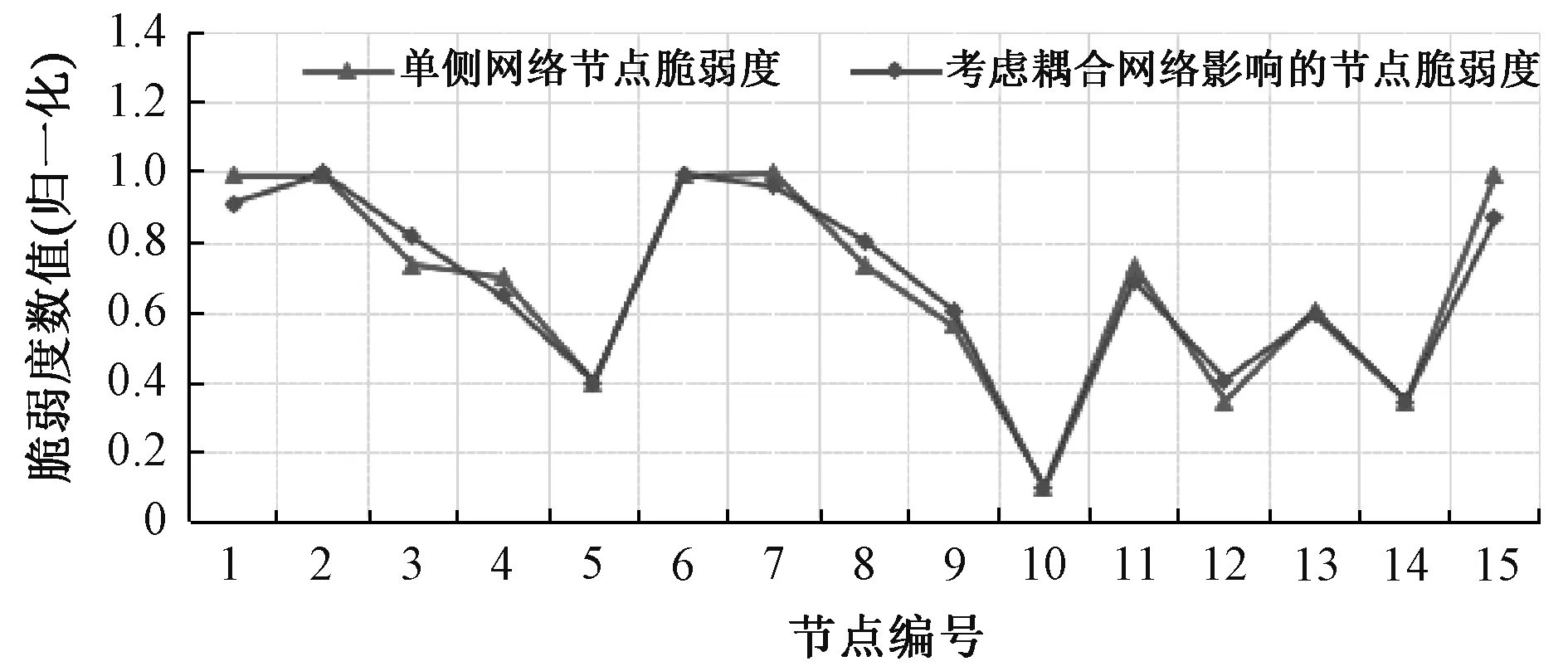
图4 信息侧节点脆弱度对比图Fig.4 Comparison chart of vulnerability of information side nodes
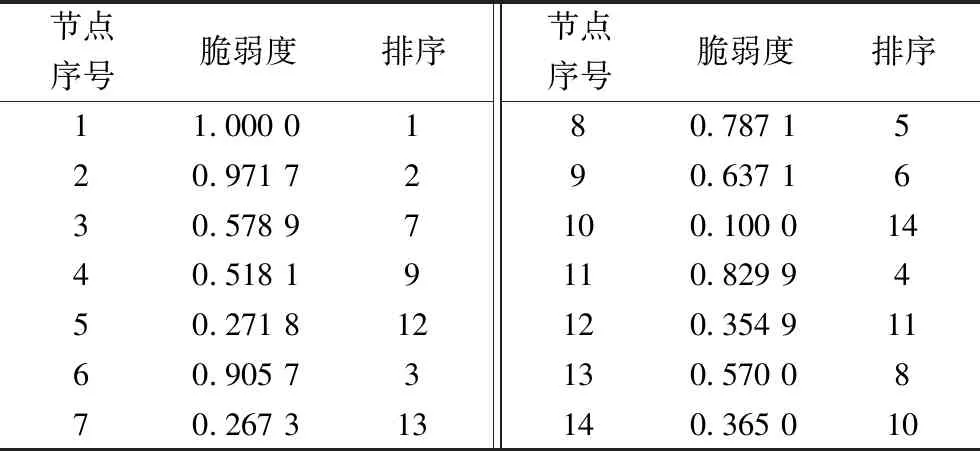
表6 考虑配电网CPS耦合特性的物理侧节点脆弱度值(取小数点后四位)Tab.6 Vulnerability value of nodes on the physical side considering the coupling characteristics of CPS in distribution network(take four digits after the decimal point)
以电力物理网节点4和13为例,仅考虑单侧网络其脆弱度值分别为0.549 8、0.550 0,因为两个节点的位置基本相同所以结果近似,耦合信息网对其影响程度分别为0.038 2、0.095 4,在考虑耦合网络的影响后,节点脆弱度变为0.518 1和0.570 0,结果差异较大,表明耦合网络会对节点的脆弱性评价产生影响,脆弱度值排序结果也由第8、7位分别变为第9、8位;就物理节点8和13而言,其信息网对其影响值分别为0.094 7、0.095 4,单侧物理网络节点脆弱度值为0.777 5、0.550 0,在依存度值差不多的情况下,考虑依存网络的影响之后脆弱度值变为0.787 1和0.570 0,表明单侧物理节点的本征脆弱度值会对CPS系统节点的脆弱度值产生影响,脆弱度值排序结果也由第5、7位变为第5、8位。将单侧物理网节点脆弱度值与考虑耦合网络依存度的影响的节点脆弱度值进行对比,结果如图5所示。
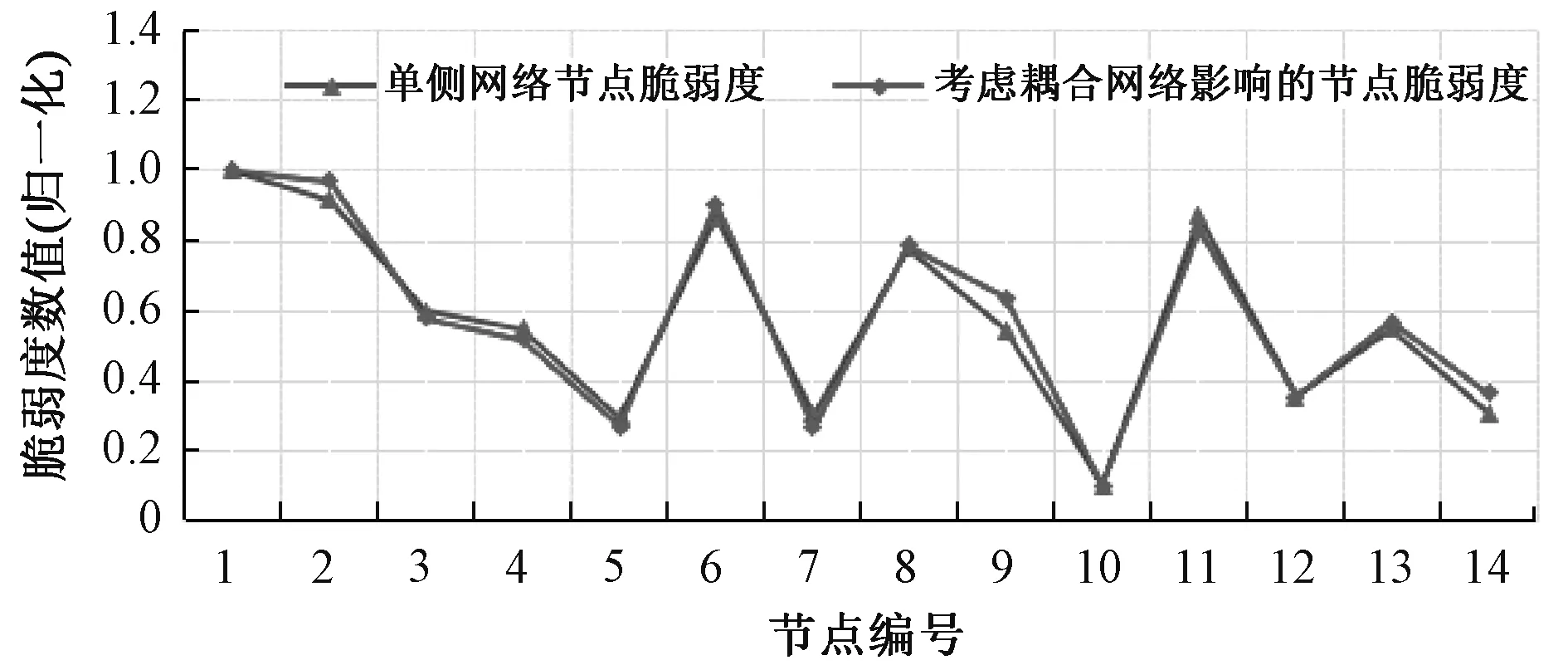
图5 物理侧节点脆弱度对比图Fig.5 Comparison of node vulnerability on the physical side
5 结 论
本文根据配电网CPS系统的特点,基于相依网络模型搭建了“部分一对一”节点相依网络模型,并提出了一种基于最小鉴别信息原理组合赋权法和TOPSIS算法的节点综合脆弱度排序的量化评估方法。在该方法下,可以对配电网CPS系统信息侧与物理侧节点进行分析,从多角度分析影响节点脆弱性的评价指标,且综合考虑了双侧节点彼此之间的影响程度。为使评估更为全面,采用模糊层次分析法与熵值法对主客观权重进行计算,并基于最小鉴别信息原理实现对主客观权重的综合度量。最后,运用TOPSIS算法对两侧节点进行了脆弱度排序,并得出各个节点的脆弱度值,基于相依网络理论,完成对信息物理耦合视角下节点脆弱度的量化评估,且通过搭建的算例模型验证了本文所提方法的有效性与合理性。
(附录请见网络版,印刷版略)

