农业技术效率对农业碳排放的影响*——基于空间溢出效应与门槛效应分析

颜光耀, 陈卫洪,2, 钱海慧

(1.贵州大学经济学院 贵阳 550000; 2.贵州省丹穴山朴门永续发展有限公司 长顺 550700)

随着温室效应的不断加剧, 由温室效应带来的气候变暖在全球范围内引发了前所未有的极端天气事件, 因此世界各国开始谋求合作共同应对随之而来的危机, 中国也提出了要在2030年前二氧化碳排放达到高峰, 力争在2060年实现碳中和的碳达峰碳中和(“双碳”)目标[1]。中国是一个农业大国, 种植业的二氧化碳排放达到全国二氧化碳排放总量的16%～17%[2], 已经成为了不可忽视的重要碳排放源。因此寻找低碳农业的实现路径, 减少农业碳排放对实现我国的“双碳”目标具有重要意义。而在众多影响农业碳排放的因素中, 农业技术已经成了促进节能减排不可忽视的重要力量[3]。2022年中央一号文件指出要研发应用减碳增汇型农业技术, 从而在发展规划层面肯定了农业技术在减少农业碳排放上起到的重要作用。从近代以来人类社会的发展史来看,技术进步会刺激生产增加能源消耗, 但同时农业技术进步能够提高能源利用效率, 降低农业碳排放强度[4], “双碳”目标约束下的减排政策也会倒逼农业技术的进步。当前中国正处于农业技术快速进步的历史时期, 各地区之间的农业技术水平差距较大, 西部地区的农业技术水平仍然有较大的进步空间。在此背景下, 为促进农业低碳绿色发展, 实现农业发展方式的转变, 就必须发挥农业技术在其中的关键性作用, 同时也是推动农业高质量发展的必然选择。

农业碳排放是指在农业生产过程中, 化肥农药的使用、能源的消耗和土地翻耕灌溉过程中直接或间接造成的温室气体(主要指二氧化碳)的排放[5]。众多学者在农业碳排放相关领域进行了大量研究,如农业碳排放的测算[6-7]和影响农业碳排放的因素[8-9]。当前有关农业技术与农业碳排放关系的研究,主要可以分为两个方面: 一是农业技术进步会显著增加农业碳排放总量, 这是由于技术进步往往会促进经济增长, 通过投入农药化肥和能源消耗等途径增加了农业碳排放[10-11]。二是农业技术进步有助于降低农业碳排放强度[4,10,12-13], 这是因为技术进步将改变不同要素之间的边际替代率, 同时提高了能源要素的利用效率, 进而影响农业碳排放强度。

农业全要素生产率(TFP)可被分解为农业技术进步(TC)、农业技术效率(TEC)、农业规模效应(SEC)和要素重置效应(FAEC)[14]。其中, 农业全要素生产率属于广义的农业技术进步; 被分解后的农业技术进步属于狭义的农业技术进步, 是指代表最先进生产技术的生产前沿面整体向外移动, 即采用新技术使得以同样的投入组合生产出更多的产出; 农业技术效率指在现有农业技术水平下, 协调各种农业资源要素, 促使现有的技术水平潜能更大程度地释放; 农业规模效应指农业生产规模的扩大带来的经济效益的提高; 要素重置效应指生产要素在市场供给方之间发生变动和重新配置[15]。现有的研究大多从农业技术进步和规模效应的角度探究其与农业碳排放的关系, 其中农业技术进步的相关研究有: 李成龙等[14]研究认为农业技术进步并不总是有利于减少农业碳排放, 其中机械型技术进步促进了农业碳排放强度的提高, 而生物型技术进步降低了农业碳排放强度。徐清华等[16]研究认为农业机械化降低了本地农业碳排放的同时, 又具有空间负向溢出效应。规模效应的研究有: 李波等[5]通过Kaya恒等式变形对农业碳排放影响因素进行分解研究, 结果表明劳动力规模对碳排放量有一定的抑制作用, 而农业经济发展则会推动农业碳排放。要素重置效应涉及各生产部门、产业组织和生产消费端的要素流动, 其对农业碳排放的影响较为复杂, 目前少有相关研究成果, 而对农业技术效率的研究也仅停留在农业技术效率与农业碳排放存在负脱钩关系[17]的研究层次上, 缺少对其影响机制进行进一步的实证分析。

综上所述, 当前对农业技术进步与农业碳排放的研究, 一方面大多数学者往往局限于广义的农业技术进步与狭义的农业技术进步对农业碳排放影响研究, 甚至在研究中不能有效地区分广义与狭义的技术进步。另一方面缺少农业技术效率和农业碳排放关系的深入研究, 使得这一研究领域长期以来处于空白状态。因此本文将以空间视角研究分析农业技术效率对农业碳排放的影响, 同时构建门槛模型以探究二者的非线性关系, 填补相关研究的空白, 为政府达到农业碳排放减排目标提供理论依据和针对性的政策建议。

1 理论分析与研究假设

本研究选取狭义农业(种植业)作为研究对象。参考李波等[5]、陈军娟等[17]和何炫蕾等[18]学者的研究, 将农业碳排放定义为在农业生产过程中产生的碳排放, 农业碳排放强度定义为每万元农业总产值引起的农业碳排放。当前对于农业碳排放影响要素研究基本认为农业碳排放具有空间溢出效应[19]。基于此, 农业碳排放强度也应当具有空间溢出效应, 且其效应为正向影响。综上所述提出如下假设:

假设1: 农业碳排放强度具有空间溢出效应, 并表现出正向效应。

农业技术效率指农业现实产出与理论最大可能产量的比率, 其数值大小反映的是生产者利用现有技术的有效程度, 取值范围介于0至1之间, 数值越大表明农业技术效率越高[20]。当前学界对于技术效率的计算大多采用随机前沿模型, 例如杨增旭等[21]利用随机前沿生产函数计算了我国小麦(Triticum aestivum)和玉米(Zea mays)化肥施用的技术效率。汪小勤等[22]运用随机前沿模型验证了农业公共投资能够促进农业技术效率提升。因此本文对比其他生产函数, 选择使用随机前沿模型计算农业技术效率。

现有的研究已经证明了农业技术效率与农业碳排放有高度相关性[17], 而农业技术的传播往往限制较低, 容易形成技术集聚。高鸣等[23]通过实证研究后发现农业技术效率不但不会随着距离的扩大而降低,甚至会通过规模效应使技术效率获得进一步提升,证明了农业技术效率存在空间自相关。张思麒等[24]研究认为“前沿型”技术进步具有正向溢出效应, “追随型”技术进步对经济发展水平相对落后的地区产生的贡献更大。基于此, 提出如下假设:

假设2: 农业技术效率具有显著的空间相关性,对邻近省份的农业碳排放具有负向空间溢出效应。

技术进步对农业碳排放的影响并非一成不变,一些学者的研究指出不同路径下技术进步对农业碳排放的影响各不相同[13]。同时技术效率的提升意味着各投入要素间的协调得到了优化, 而这种协调的优化并不等同于要素投入的减少, 甚至可能促进要素的投入。此外, 杨义武等[25]认为农业技术进步与技术效率同时具有边际效应, 边际效应的存在也使得农业技术效率对碳排放产生非线性影响。Wang[26]认为门槛模型能够有效解决变量间的非线性关系问题。因此本文采用Hansen[27]提出的面板数据门槛回归模型, 探究农业技术效率与农业碳排放强度存在的非线性相关关系, 相应的假设如下:

假设3: 农业技术效率与农业碳排放强度具有非线性相关关系, 并存在门槛效应。

2 研究方法

2.1 变量选取与度量

2.1.1 被解释变量: 农业碳排放

本文将农业碳排放设定为农业碳排放强度, 含义为每万元农业GDP所产生的碳排放量, 为避免价格因素带来的影响, 本文以2001年为基准的不变价格种植业总值表示农业GDP。参考学者李波等[5]的研究, 农业碳排放主要来源为农业生产活动中化肥、农药和农膜的生产与使用、农业机械的燃料消耗、农地翻耕和农业灌溉导致的土壤有机碳流失。据此可构建农业碳排放计算公式如下所示:

式中:C为农业碳排放总量;Ci为对应碳源的农业碳排放量;Ti为对应碳排放源的量;δi为对应碳源的碳排放系数, 其具体数值如表1所示。

表 1 各类农业碳排放源的碳排放系数及其来源Table 1 Carbon emission coefficient of each carbon source of agriculture and its reference source

因各地区农业规模存在较大差异性, 仅以农业碳排放总量衡量地区农业碳排放水平缺少说服力,而农业碳排放与农业经济发展水平密不可分, 因此本文选择将农业碳排放强度作为被解释变量。其计算公式为:

式中:i为省份,t为时间,Cit为农业碳排放总量, CIit为农业碳排放强度, GCPit为不变价格的种植业总产值。

2.1.2 解释变量: 农业技术效率

与要求技术中性、规模报酬不变的传统柯布-道格拉斯(C-D)生产函数和不变替代弹性生产函数(CES)不同, 超越对数生产函数允许各投入要素之间的替代弹性是可变的, 并能反映出投入要素的交叉效应对产出变量的影响[32]。因此本文通过构建超越对数生产函数的随机前沿模型计算各地区历年农业技术效率。借鉴白俊红等[33]和李成龙等[14]的模型构建思路, 构建具体的模型如下:

式中:i为省份;t为时间;Yit为农业总产出, 本文以不变价格的种植业总产值表示(亿元);xnit、xmit分别为第n个投入量和第m个投入量, 本文选取的投入要素为第一产业从业人员数(万人)、农作物播种总面积(hm2)、农业机械总动力(万kW)、化肥施用量(万t);T表示技术效率变化的时间趋势;α表示各参数系数;vit表示随机误差项;μit代表技术无效因素,二者互相独立并服从正态分布。基于此, 农业技术效率的计算公式为:

式中: ATEit为农业技术效率, 取值范围为0＜ATEit≤1, 数值越大表明农业技术效率越高。

2.1.3 控制变量

参照现有文献[5,8-9,11,14,16,19], 总结归纳影响农业碳排放的影响因素, 将农业经济发展水平、人力资本水平、农业受灾程度和人均耕地面积等4个变量设置为控制变量。为了更贴近农村劳动力现实情况,本文选取各省份农村地区初中及其以上学历人数与农村地区6岁以上总人数的比率作为衡量人力资本水平的指标。

2.2 数据说明及描述性统计

考虑到数据的可获得性与实际情况, 本文以港澳台地区以外, 中国31个省、直辖市和自治区2001-2020年共20年的面板数据作为分析样本, 相关统计数据来源于《中国统计年鉴》《中国农村统计年鉴》《中国人口统计年鉴》《中国人口与就业统计年鉴》和各省(直辖市、自治区)统计年鉴, 在不影响结果的前提下对极少部分缺失数据使用插值法补齐, 总结归纳各变量设定及描述性统计情况如表2所示。

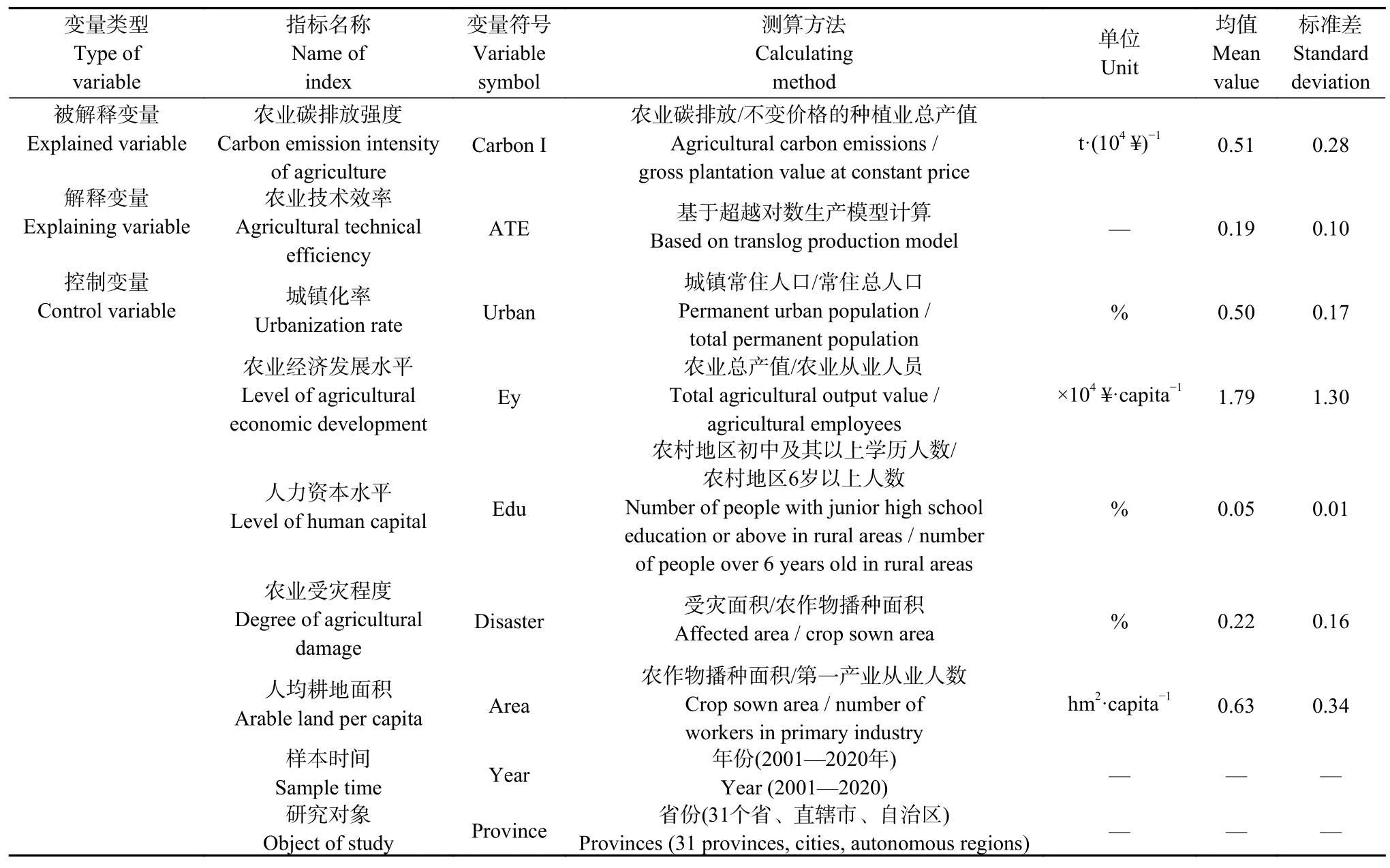
表 2 农业碳排放研究相关变量说明及描述性统计Table 2 Description and descriptive statistics of related variables of agricultural carbon emission research

2.3 模型建立

2.3.1 空间自相关检验

对变量的空间相关性分析, 首先必须明确变量是否存在空间效应, 而检验空间效应最常用的方法是计算Moran’sI指数。因此构建全局Moran’sI指数模型, 对农业碳排放强度和农业技术效率的空间自相关性进行检验。公式如下:

式中:I为全局Moran’sI指数;n为选取省份的个数,本文n=31;xi、xj为i省份和j省份的农业碳排放强度和农业技术效率;为样本平均值;wij为邻接空间权重矩阵, 当i与j不相邻时设置为0, 反之则为1。全局Moran’sI指数服从正态分布, 其取值范围为[-1, 1], 当Moran’sI指数为0时, 说明变量间不存在空间相关性; 当Moran’sI指数大于0时, 说明变量间存在空间正相关性; 当Moran’sI指数小于0时, 说明变量间存在空间负相关性; Moran’sI指数的绝对值越大, 说明其相关性越强。

2.3.2 空间面板回归模型

式中:τ、ρ、β均为系数;yi,t-1为被解释变量的一阶滞后;w′iXtδ 为解释变量的空间滞后;w′i为空间权重矩阵W的第i行; γt为时间效应;为扰动项空间权重矩阵M的第i行;ui为区域i的个体效应;εit为残差;εt为空间滞后误差项;vit为随机误差项。

为考虑不同情况下农业碳排放空间溢出效应的差异性, 本文构建3种空间权重矩阵, 其具体含义如下所示:

式中:d为地区i与j的距离, 本文将各省省会之间的距离作为衡量距离的指标。

空间面板回归模型的具体形式一般根据LM检验、LR检验、Wald检验和Hausman检验的结果来确定。其中, Hausman检验用于确定模型使用固定效应或随机效应, 本文Hausman检验的原假设为“支持模型使用随机效应”; LM检验用于确定模型是否存在空间自相关性, 其原假设为“模型不存在空间自相关”; LR检验与Wald检验用于确定模型是否使用空间误差模型(SEM)或空间滞后模型(SLM), 其原假设为“空间杜宾模型(SDM)不能简化为空间误差模型或空间滞后模型”。

根据以上检验结果, 对公式(6)进行改进补充。如果模型为空间杜宾模型, 则λ=0; 若模型为空间滞后模型, 则λ=0且δ=0; 若模型为空间误差模型, 则τ=ρ=0且δ=0。

2.3.3 门槛回归模型

效率的提升并不代表投入要素的减少, 甚至可能促进要素的投入, 此外技术效率具有边际效应, 因而农业技术效率对农业碳排放的影响可能是非线性的。综上所述, 本文参考Hansen[27]的面板回归模型,依照本文理论分析中的研究假设, 将农业碳排放强度(Carbon I)作为被解释变量, 农业技术效率(ATE)同时作为门槛变量和核心解释变量, 构建门槛回归模型, 公式如(10)所示:

式中:θ1,θ2, · ··,θn表示n个不同水平的门槛值; Control表示控制变量;D(·)为指标函数;μit为随机扰动项。

3 结果与分析

3.1 农业碳排放变化规律

依据公式(1)、(2), 按照国家统计局关于东中西部的划分, 将北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东和海南划分为东部地区, 山西、吉林、黑龙江、安徽、江西、河南、湖北和湖南为中部地区, 内蒙古、广西、重庆、四川、贵州、云南、西藏、陕西、甘肃、青海、宁夏和新疆为西部地区, 计算2001-2020年中国不同地区农业碳排放总量和农业碳排放强度, 所得农业碳排放总量和农业碳排放强度分区域趋势变化图如图1所示。

图 1 2001—2020年中国不同地区农业碳排放总量(a)和农业碳排放强度(b)Fig.1 Total amount (a) and intensity (b) of agricultural carbon emissions in different regions of China from 2001 to 2020

从图1可以看出, 2001-2020年各地区农业碳排放总量表现为上升趋势, 但自2015年以后有所降低, 而农业碳排放强度则一直保持下降趋势。分区域来看, 中部地区的农业碳排放总量高于东部与西部, 这是因为中部地区包括河南、黑龙江、吉林在内均为农业大省, 拉高了农业碳排放总量。农业碳排放强度则是东部地区低于中西部地区, 这主要是因为东部地区农业技术水平、城镇化率等显著降低农业碳排放强度的指标优于中西部地区。以2020年为例, 农业碳排放总量(万t)最高的10个省(直辖市、自治区)为河南(1237.51)、山东(961.28)、黑龙江(828.12)、安徽(683.90)、河北(681.71)、江苏(648.55)、新疆(624.42)、四川(613.10)、湖北(608.25)和湖南(589.34)。农业碳排放强度(t·万元-1)最高的10个省(直辖市、自治区)为内蒙古(0.48)、吉林(0.44)、安徽(0.34)、新疆(0.31)、宁夏(0.31)、山西(0.30)、甘肃(0.27)、上海(0.25)、青海(0.25)和黑龙江(0.25)。

图 2 2001—2020年中国不同地区农业技术效率Fig.2 Agricultural technical efficiencies in different regions of China from 2001 to 2020

结合以上数据可知, 以农作物播种总面积衡量的农业大省所产生的农业碳排放总量相对较高, 中部地区的碳排放总量较高, 西部地区的农业碳排放强度较高。中国地域广大, 幅员辽阔, 各地区的农业生产要素禀赋各不相同, 是造成这些差异的主要原因。因此各地区应当依据自己的农业发展情况, 实事求是地制定合理的碳减排目标。

3.2 农业技术效率变化规律

构建超越对数生产函数, 依据公式(3)和(4)计算历年各区域农业技术效率, 结果如图2所示。由图2结果可知, 2001-2020年各地区农业技术效率水平不断提高, 东部地区农业技术效率显著高于中西部地区, 而中部地区仅略微高于西部地区, 且二者均低于全国平均水平。分省市来看, 20年平均农业技术效率高于全国平均水平(0.186)的省市从大到小依次为: 北京(0.381)、上海(0.286)、浙江(0.280)、天津(0.238)、福建(0.231)、广东(0.224)、辽宁(0.223)、海南(0.223)、山东(0.211)、河北(0.206)和江苏(0.196); 低于全国平均水平从小到大依次为: 内蒙古(0.124)、安徽(0.129)、宁夏(0.137)、青海(0.137)、贵州(0.139)、山西(0.141)、云南(0.141)、江西(0.152)、广西(0.155)、湖北(0.155)、黑龙江(0.156)、陕西(0.157)、重庆(0.157)、甘肃(0.162)、河南(0.164)、四川(0.168)、吉林(0.169)、湖南(0.175)、西藏(0.78)和新疆(0.180)。

对比分析各地区农业技术效率差异可知, 东部沿海省市的农业技术水平远高于内陆省份。与此同时, 随着农村劳动力转移进城, 中西部地区农业生产水平却依旧维持在较低水平, 而未来中国的农业发展方式也要从过去的粗放式低效益转变为产业化、生态化、国际化和地区化。在这样的背景下, 中西部地区要积极学习借鉴东部沿海省市的发展经验,引进新型农业机械和信息化管理技术, 才能从根本上解决当前农业发展中存在的问题。考虑到北京、上海、天津第一产业产值分别位列全国各省(直辖市、自治区)倒数第2、第1和第4, 浙江省在提高农业技术效率上的经验更具有参考价值, 值得其他各省市学习。

3.3 农业碳排放与农业技术效率的空间自相关性检验结果分析

基于空间面板数据, 利用Stata 16软件参照公式(5)计算2001-2020年农业碳排放强度与农业技术效率的全局Moran’sI指数和2020年农业碳排放强度与农业技术效率的局部Moran’sI指数, 结果分别如表3和图3所示。

由表3可知, 2001-2020年农业碳排放强度与农业技术效率的全局Moran’sI指数均为正, 且通过P＜0.05显著性检验, 说明农业碳排放强度与农业技术效率存在显著空间相关性并表现出集聚的特征。从时间变化来看, 农业碳排放强度的Moran’sI值随着时间推移表现为上下波动后上升, 说明农业碳排放强度的聚集程度呈增强趋势; 农业技术效率的Moran’sI值随着时间推移表现持续升高趋势, 说明农业技术效率的聚集程度在逐渐增强。

Moran’sI散点图可形象表现地区间的空间相关性, 其含义为第1象限内的省份农业碳排放强度或农业技术效率较高, 形成了高高集聚; 第2象限内的省份自身水平较低而周边水平较高, 形成了低高聚集; 第3象限内的省份自身水平较高而周边水平较低, 形成了高低聚集; 第4象限内的省份自身水平较低的同时周边水平同样较低, 形成了低低聚集。从结果来看, 农业碳排放强度形成高高聚集的省份共有10个, 低高聚集的有5个, 高低聚集的有4个, 低低聚集的有12个, 主要以高高聚集和低低聚集为主;农业技术效率形成高高聚集的有9个, 低高聚集的有2个, 高低聚集的有2个, 低低聚集的有18个, 同样以高高聚集和低低聚集为主。

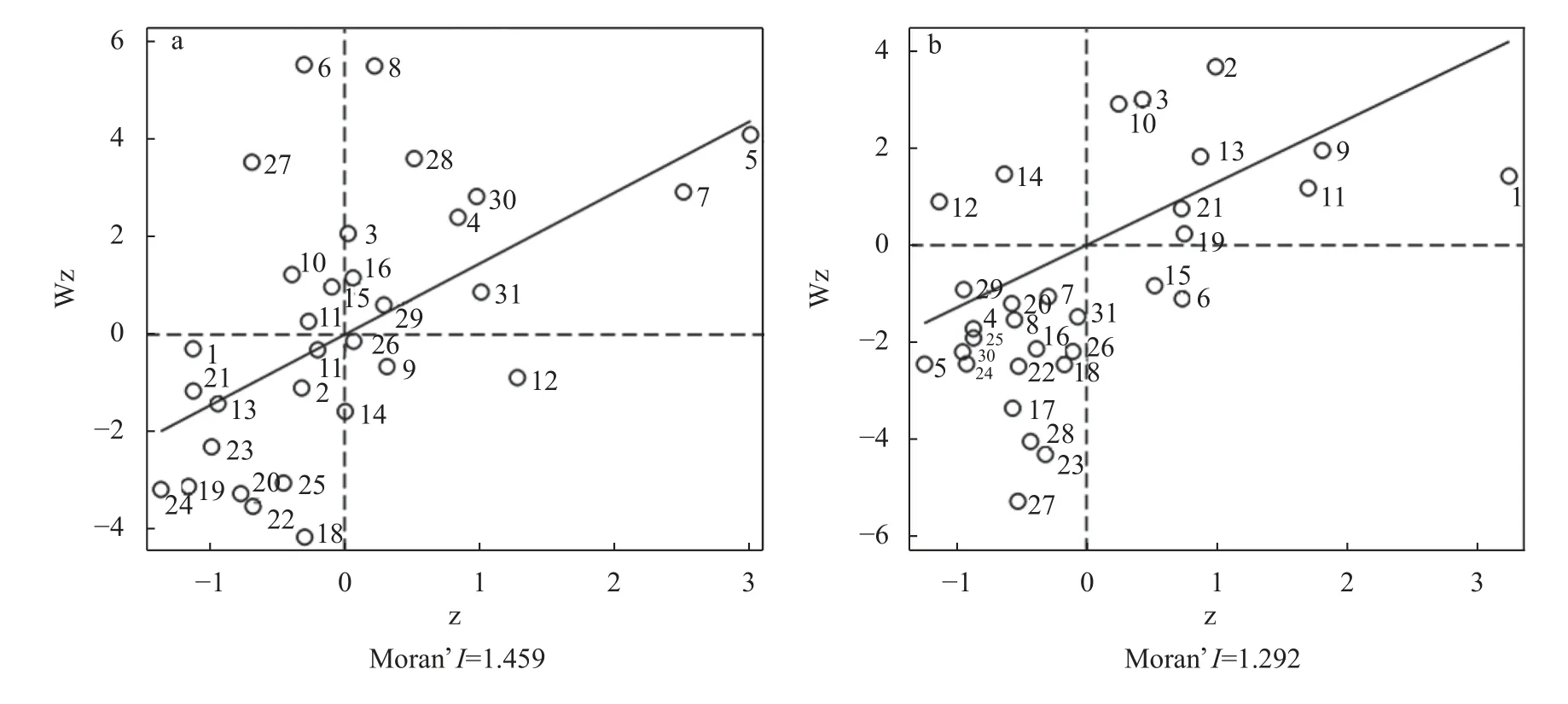
图 3 2020年农业碳排放强度(a)与农业技术效率(b) Moran’s I散点图Fig.3 Moran’s I scatter diagrams of agricultural carbon emission intensity and agricultural technical efficiency in 2020

表 3 2001—2020年农业碳排放强度和农业技术效率的全局Moran’s I指数及检验Table 3 Moran’s I indexes and test of agricultural carbon emission intensity and agricultural technical efficiency from 2001 to 2020

上述结果表明, 农业碳排放强度与农业技术效率显著存在空间相关性, 聚集类型均以高高聚集和低低聚集为主。根据上文空间面板数据模型构建的前提条件, 本文将进一步对农业技术效率对农业碳排放的空间溢出效应进行检验分析。

3.4 农业技术效率对农业碳排放强度的空间面板回归模型选择

根据空间自相关检验的结果, 农业碳排放强度与农业技术效率的全局Moran’sI指数显著且不等于0, 说明变量存在空间相关性, 可以对其进行进一步分析, 确定其所使用的空间面板回归模型。分别对3种空间权重矩阵的空间面板回归模型进行LM检验、LR检验、Wald检验和Hausman检验, 所得结果如表4所示。

由表4可知, 邻接空间矩阵、地理距离矩阵和经济距离矩阵的空间面板模型均通过LM检验拒绝原假设, 表明模型存在空间交互效应, 且空间误差模型显著水平优于空间滞后模型; LR检验与Wald检验结果均表明拒绝原假设, 应将模型设置为空间杜宾模型; Hausman检验与拟合度分析结果表明应选择个体固定效应模型。

综上所述, 根据LM检验、LR检验和Hausman检验结果, 确定3种空间权重矩阵的空间面板模型均为个体固定效应的空间杜宾模型, 构建模型公式如下所示:

式中:i为省份;t为时间;ρ为空间回归相关系数, 表示相邻地区的被解释变量对本地区被解释变量的影响;β1～β6表示本地区解释变量对本地区被解释变量的影响程度;θ1～θ6表示相邻地区解释变量对本地区被解释变量的影响程度;Wj为空间权重矩阵,j=1,2,3,分别表示邻接空间矩阵、地理距离矩阵和经济距离矩阵; Acarbon为被解释变量; ATE、Urban、Ey、Edu、Disaster、Area为解释变量, 具体意义见表2;μi为i地区的个体效应;εit为随机误差项。

3.5 农业技术效率对农业碳排放强度的空间杜宾模型回归结果分析

将3种矩阵的模型均设置为个体固定效应的空间杜宾模型, 使用Stata 16软件对其分别进行回归分析, 所得结果分别如表5、表6和表7所示。

表5、表6和表7的结果表明, 3种空间权重矩阵在个体固定效应空间杜宾模型下, 农业碳排放强度空间自回归项rho的系数为正, 且均通过了1%显著性检验, 说明农业碳排放强度具有正向的空间溢出效应, 本省农业碳排放强度的提高会促进邻省的农业碳排放强度的上升, 据此假设1得到验证。此外, 根据LeSage等[34]的研究, 若被解释变量的空间自相关rho系数显著且不为0, 则不能直接使用空间矩阵估计系数Wx的回归系数衡量解释变量对被解释变量的空间溢出效应, 应当使用偏微分法得到解释变量的无偏估计结果, 即直接效应、间接效应和总效应。

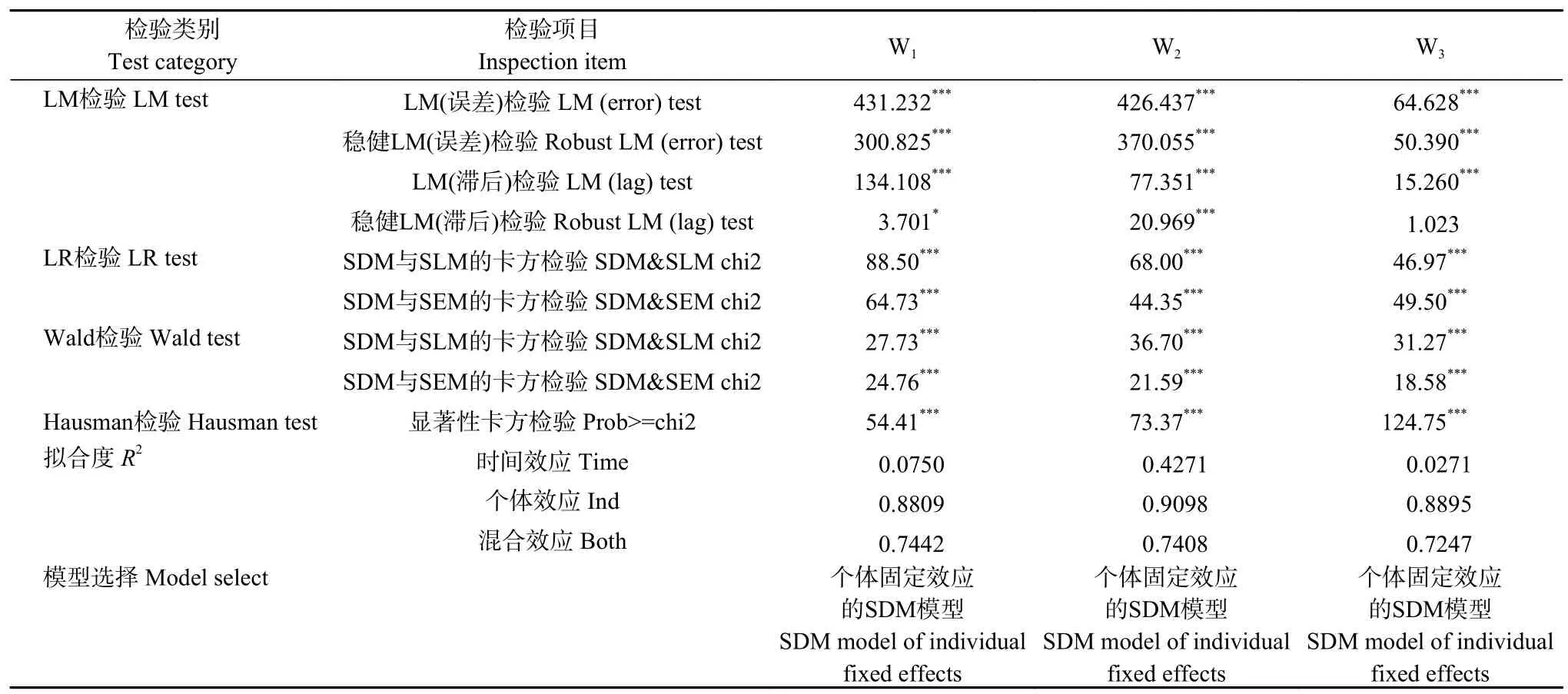
表 4 农业技术效率对农业碳排放强度空间面板回归模型的LM检验、LR检验、Wald检验和Hausman检验结果Table 4 Results of LM test, LR test, Wald test and Hausman test of the spatial panel regression model of agricultural technical efficiency to agricultural carbon emission intensity

表 5 农业技术效率对农业碳排放强度的邻接空间矩阵空间杜宾模型回归结果及效应分解Table 5 Regression results and effect decomposition of the adjacency space matrix spatial Durbin model of agricultural technical efficiency to agricultural carbon emission intensity

1)农业技术效率。农业技术效率在3个空间权重矩阵模型中, 直接效应均表现为显著正向影响, 间接效应和总效应则表现为显著负向影响。农业技术效率的提高会刺激农业要素的投入, 此时每一单位的要素投入将会带来更多的农业产出, 表现为边际效应递增。而农业碳排放也将随着农业产量的提升而增大, 因此农业技术效率的提升将促进农业碳排放。而间接效应为负, 则证明了农业技术具有“示范效应”, 邻近省份学习先进的农业技术, 可以有效降低该省的农业碳排放强度, 并且从总效应结果上看,农业技术效率的提高归根结底有利于抑制农业碳排放, 据此假设2得到验证。

2)城镇化。城镇化在3个空间权重矩阵模型中,直接效应和总效应表现为显著负向影响, 间接效应未表现出显著性。就业城镇化的含义是农村地区的人口转移至城镇就业从而实现的城镇化, 就业人口的城镇化促进了农业要素投入的集约化, 从而降低了农业碳排放强度。因此, 提高就业城镇化率, 能够降低农业碳排放强度。

3)农业经济发展水平。农业经济发展水平在3个空间权重矩阵模型中, 直接效应表现为显著负向影响, 而间接效应和总效应则表现为显著正向影响。农业经济发展水平的提升意味着要素投入减少的同时反而有更多的产出, 这意味着同等产出水平下所投入的要素量减少了, 这使得农业碳排放也降低了。然而本地区农业经济发展水平的提高并不能降低相邻地区农业碳排放强度, 这可能是因为存在“挤出”效应, 农业经济发展水平较高的地区占据了较多的“低碳资源”, 使得邻近地区在降低农业碳排放强度上不具有相对优势。总体上看, 农业经济发展水平对农业碳排放强度有促进作用。

4)人力资本水平。人力资本水平在3个空间权重矩阵模型中, 间接效应和总效应表现为显著负向影响, 直接效应则未表现出一致影响方向。总的来看, 人力资本水平的提升意味着劳动力素质的提升,农业劳动者将更善于利用先进的农业生产技术与管理手段, 促使农业生产在更低的要素投入下拥有更高的产量, 节约了能源消耗, 促进了农业碳排放强度降低。此外, 邻近地区的农业从业人员也通过学习先进技术, 使人力资本水平对邻省农业碳排放强度具有负向的空间溢出效应。因此, 人力资本水平越高, 农业碳排放强度越低。

5)农业受灾程度。农业受灾程度在3个空间权重矩阵模型中, 直接效应、间接效应和总效应均表现为正向影响。农业耕作受到破坏后, 将在短时间内投入大量要素对其进行重建, 从而大幅度提高碳排放, 因此其对农业碳排放强度的影响为正, 而农业灾害具有规模范围性, 往往连片出现, 因此表现出正向空间溢出效应。总体而言, 农业受灾程度越深, 农业碳排放强度越高。

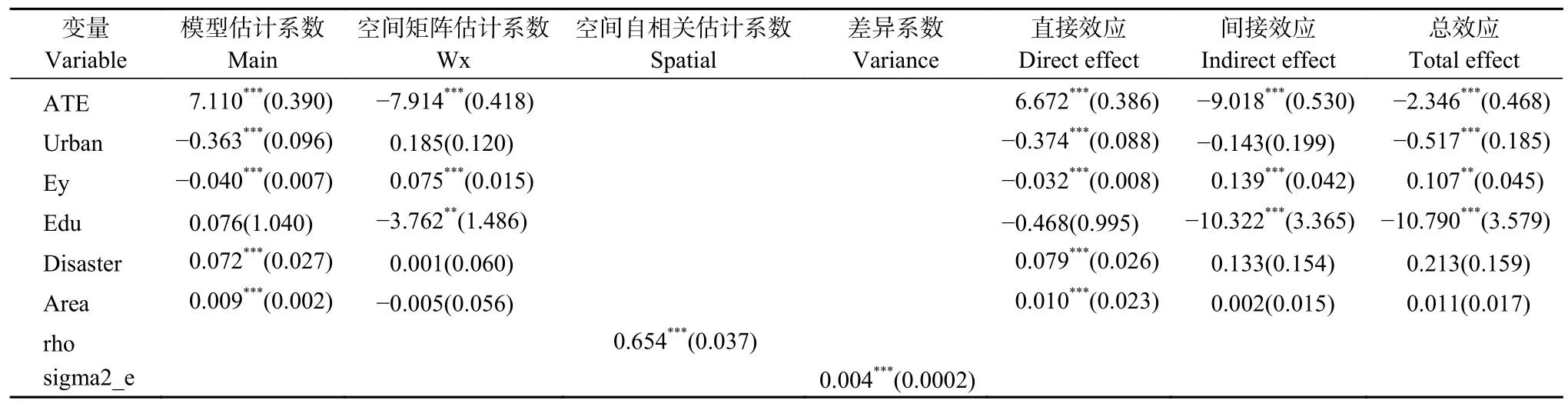
表 6 农业技术效率对农业碳排放强度的地理距离矩阵空间杜宾模型回归结果及效应分解Table 6 Geographical distance matrix spatial Durbin model regression results and effect decomposition of agricultural technical efficiency to agricultural carbon emission intensity

表 7 农业技术效率对农业碳排放强度的经济距离矩阵空间杜宾模型回归结果及效应分解Table 7 Economic distance matrix spatial Durbin model regression results and effect decomposition of agricultural technical efficiency on agricultural carbon emission intensity

6)人均耕地面积。人均耕地面积在3个空间权重矩阵模型中, 直接效应均表现为显著正向, 地理距离矩阵的间接效应与总效应表现为正向但未显著,邻接空间矩阵与经济距离矩阵的间接效应与总效应表现为显著负向。人均耕地面积的提升意味着农业耕地面积、能源消耗和农资消耗的增加, 从而促进了本地区农业碳排放强度的增加, 而本地区人均耕地面积的增加使得相邻地区的农业要素被大量转移,使得相邻地区的农业碳排放有所降低。从整体来看,人均耕地面积的增加能够降低农业碳排放强度。

3.6 农业碳排放研究中变量的多重共线性检验

为了避免变量间存在影响研究结果的严重多重共线性, 本文使用Pearson相关系数法和VIF检验对其进行多重共线性检验, 结果如表8所示。

表 8 农业碳排放研究中变量的Pearson相关系数及VIF检验结果Table 8 Pearson correlation coefficient and VIF test results of variables in the study of agricultural carbon emissions

模型中可能存在严重多重共线性的Pearson相关系数上限值为0.7[35], 而本文回归模型变量的Pearson相关系数绝对值均小于0.6。此外, 方差膨胀因子(VIF)判断是否存在多重共线性的标准为: 1)VIF的最大值小于10; 2)VIF的均值大于1。本文VIF检验结果显示, 变量中VIF最大值为2.66＜10, VIF平均值为1.81＞1, 满足不存在严重多重共线性的两个条件。综上所述, 本文各变量间不存在严重多重共线性。

3.7 农业碳排放研究中变量的单位根检验与协整检验

针对模型回归中可能出现的伪回归, 参考郭庆旺等[36]的方法, 对各变量进行单位根检验和协整检验。面板数据单位根检验根据面板数据的特征共有5种检验方法, 鉴于本文所使用的面板数据为短面板数据, 应当使用HT检验和IPS检验, 本文额外使用LLC检验意在提高检验结果的可靠性, 所得单位根检验结果如表9所示。

根据表9结果, 各变量均通过了单位根检验, 表现出变量的平稳性, 但因对部分变量进行了一阶和二阶差分处理, 而在原始模型中本文仍旧使用原序列进行回归, 因此需对面板数据模型进行协整检验,所得结果如表10所示。协整检验结果显示Pedroni检验、Kao检验和Westerlund检验均高度显著通过协整检验。综合单位根检验和协整检验结果, 说明变量存在长期均衡关系, 不存在伪回归情况。

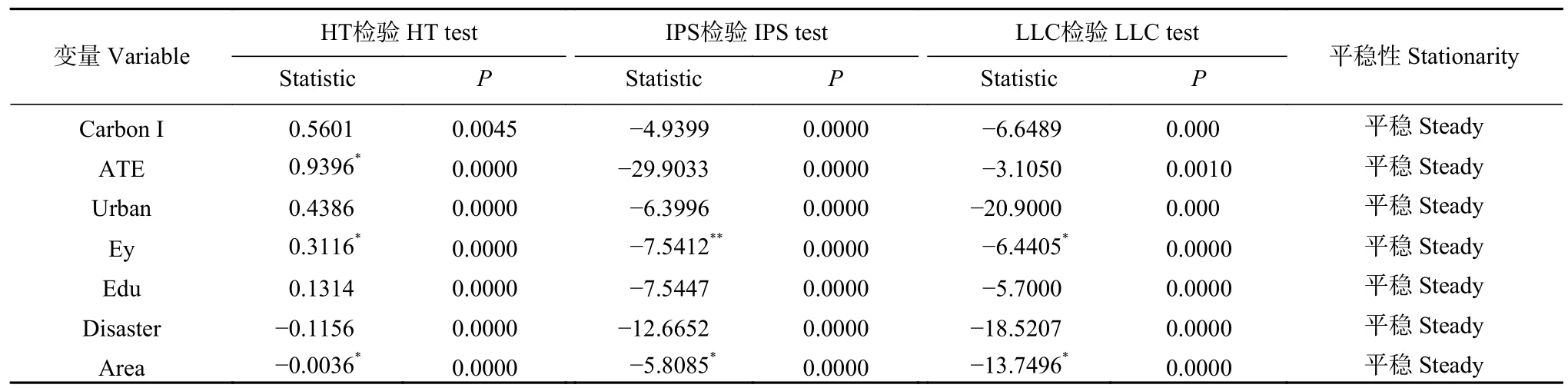
表 9 农业碳排放研究中变量的单位根检验结果Table 9 Results of unit root tests for variables in agricultural carbon emissions research

表 10 农业碳排放研究中变量的协整检验结果Table 10 Cointegration test results of the variables in the study of agricultural carbon emissions

3.8 农业技术效率对农业碳排放强度的门槛效应检验

在门槛效应回归前应对其进行Hausman检验,在固定效应和随机效应之间做出选择, 结果表明固定效应更适合本模型。因此使用固定效应模型进行门槛效应检验, 确定门槛个数和门槛效应是否存在,在stata16中输入门槛指令, 并使用Bootstrap反复抽样300次, 所得检验结果如表11所示。

表 11 农业技术效率对农业碳排放强度的门槛效应检验结果Table 11 Test results of threshold effect of agricultural technical efficiency on agricultural carbon emission intensity

门槛效应检验结果显示模型通过单一门槛和双重门槛检验, 未通过三重门槛检验, 表明农业技术效率与农业碳排放强度存在双重门槛效应。

3.9 农业技术效率对农业碳排放强度的门槛模型估计结果分析

根据门槛效应检验结果可知, 回归模型为双重门槛模型, 据此将公式(10)设置为双门槛, 并对面板数据进行门槛回归, 所得结果如表12所示。

门槛模型的回归结果表明, 当农业技术效率(ATE)低于第一门槛值0.0746时, 农业技术效率的系数估计值为0.496, 这说明农业技术效率的提升能够提高农业碳排放强度, 但此时结果并不显著; 当农业技术效率水平介于0.0746和0.2590之间时, 此时的系数估计值为-2.122, 这说明当农业技术效率越过拐点后, 其对农业碳排放强度的影响将转变为负向; 当农业技术效率提高到0.2590以上时, 系数估计值会降低到-1.538, 说明农业技术效率达到转变为边际效益递减的临界值后, 农业技术效率对农业碳排放仍然有减排作用, 但其影响力已经不如上一个门槛阶段, 据此假设3得到验证。

以门槛值作为分类标准, 将2015年31个省、直辖市和自治区(港澳台地区以外)农业技术效率进行分类, 所得结果如表13所示。分类结果显示, 技术效率较高(ATE＞0.2590)的地区均为东部沿海地区, 中国各省均跨过了第一阶段门槛区间, 进入到农业技术效率有效促进农业碳减排的发展区间。

综上所述, 农业技术效率的提升会促进农业碳排放强度的降低, 但其影响是非线性的。在不同区间内, 农业技术效率对农业碳排放的影响程度存在差异。其中, 当农业技术效率低于0.0746时, 技术效率对农业碳排放强度的影响为负向; 当高于0.0746后, 将转变为显著负向效应; 进一步提高农业技术效率并高于0.2590后, 负向效应会减弱。结合表13的分类结果, 截至2015年中国所有省份已经跨过了“拐点”, 未到达第二门槛值的省份应当继续提升农业技术效率, 发挥农业技术在低碳农业发展中的关键性作用。

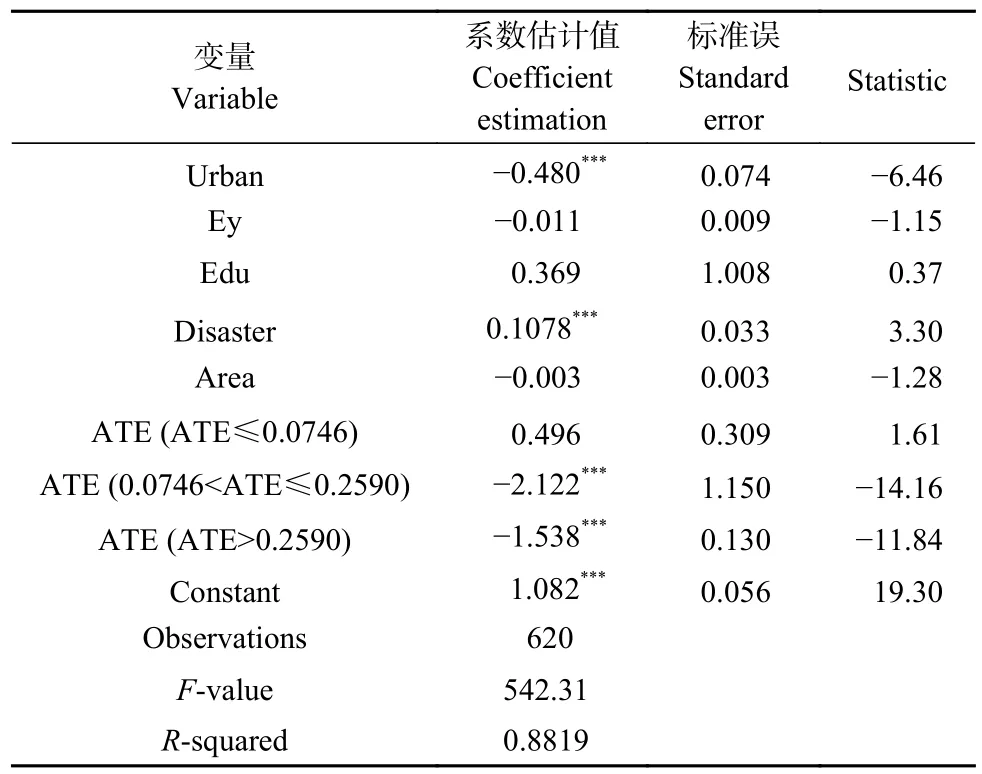
表 12 农业技术效率对农业碳排放强度的门槛模型回归估计结果Table 12 Threshold model regression estimation results of agricultural technical efficiency on agricultural carbon emission intensity

表 13 农业技术效率门槛值及省份分布(2015年)Table 13 Agricultural technical efficiency threshold and provincial distribution (2015)

4 讨论与结论

4.1 讨论

本文基于港澳台地区以外, 中国31个省、直辖市和自治区2001-2020年的面板数据, 对农业碳排放总量、农业碳排放强度和农业技术效率进行了测算, 剖析了农业碳排放强度和农业技术效率的空间相关性, 利用空间杜宾模型和门槛模型, 分别探究了农业技术效率对农业碳排放强度的空间溢出效应和农业技术效率与农业碳排放强度的非线性关系。在YANG等[4]、杨钧[11]、李成龙等[14]和徐清华等[16]学者的研究基础上, 本文从技术效率的角度出发, 进一步探究了农业技术效率与农业碳排放强度的空间效应和非线性关系。现有的研究大多将研究范围局限于广义的技术进步或狭义的技术进步, 缺少对技术效率进行深入探索, 本文将广义的技术进步分解后的技术效率作为核心, 进一步验证了技术进步对农业碳排放的空间影响机制与边际效应, 为探索实现“双碳”目标的路径提供理论基础与政策依据。

4.2 结论

本文主要结论: 1)总体上各地区农业碳排放总量和强度均表现出下降趋势, 空间分布上中部地区农业碳排放总量高于东西部地区, 东部地区农业碳排放强度低于中西部地区。农业技术效率水平则随时间逐年提高, 东部地区农业技术效率显著高于中西部地区, 而中部地区仅略微高于西部地区。2)农业技术效率与农业碳排放强度具有高度空间相关性并表现出集聚的特征, 聚集类型均以高高聚集和低低聚集为主。3)空间杜宾模型结果表明, 本省农业碳排放强度的提高会促进邻省的农业碳排放强度的上升, 具有正向空间溢出效应, 而农业技术效率对农业碳排放强度则表现为负向空间溢出, 并在总体上有利于抑制农业碳排放。此外城镇化、人力资本水平和人均耕地面积对农业碳排放强度具有负向影响,农业经济发展水平和农业受灾程度则为正向影响。4)农业技术效率与农业碳排放强度存在双门槛效应,当农业技术效率越过“拐点”(0.0746)后, 其对农业碳排放强度的影响转变为负向, 当进一步提升农业技术效率水平后, 其影响力会因边际效应递减而减弱。

对策建议: 1)各省市应依照自身农业发展实际情况, 制定符合本省省情的碳减排目标。不拘泥于农业碳排放总量的变化, 而是将农业碳排放强度作为衡量减排成效的标准。2)积极推动建立农业数据库和农作物检测系统, 应用地理信息遥感技术和计算机网络虚拟技术等数字化农业技术, 发挥农业技术的关键性作用, 提高农业技术效率, 推进新型农业技术革命, 推动传统农业迈向现代化农业。3)重视农业生产技术的传播, 将东部地区先进的农业技术手段推广到中西部地区, 促进中西部地区农业生产方式从原本的粗放型转变为产业化、生态化、集约化和低碳化。