鲁棒性幅值指数自适应谱幅值调制法
林云, 郭瑜, 刘珍
(昆明理工大学 机电工程学院,昆明 650500)
齿轮箱故障引起的振动信号通常为多源耦合信号,为提取故障特征,常采用信号处理技术将信号中包含的特征分量有效分离出来。目前常用的信号分离方法主要有同步平均[1]、自参考自适应消噪技术[2](SANC)、离散随机分离[3](DRS)和倒谱预白化[4](CPW)等,其中CPW不需要针对不同的故障情况提前设置参数即可有效降低齿轮信号等离散分量的影响,在应用中取得了较好的效果[5-7]。但值得指出的是,该技术将倒谱幅值置零来提升故障冲击成分的同时,会无差别地提升噪声成分的幅值。Moshrefzadeh等[8]近期提出的谱幅值调制(Spectral amplitude modulation, SAM)通过可变幅值指数弥补了CPW的不足,可以较灵活地适应不同的故障情况。尽管SAM技术在CPW基础上作了很好的改进,但目前SAM技术在选取幅值指数值上仍需人工判断,不适合实现对故障特征的自动提取,且当故障特征受到复杂干扰时,人工选择较难选取出较佳的幅值指数,易造成误诊。为实现在干扰环境下SAM对故障特征的自适应提取,本文提出一种鲁棒性幅值指数自适应SAM法。该方法先利用角域重采样将信号转换到角域,通过MOMEDA[9](Multipoint optimal minimum entropy deconvolution, MOMEDA)对故障弱冲击特征进行增强,再利用2阶循环平稳指标[10](ICS2)自适应选取SAM中的倒谱幅值指数,以该优化幅值指数计算倒谱信号,实现故障特征的自动提取。研究中通过行星轴承内圈故障特征提取实验验证了本文方法的有效性。
1 谱幅值调制法简介
谱幅值调制法(SAM)利用原始信号实倒谱和相位谱来重构信号,通过设置不同的实倒谱幅值的幂次来增强信号中的特定周期成分。该方法本质上相当于一个非线性滤波器[8],具有较好的鲁棒性,不需要选择优化解调频带也可以有效提取轴承故障特征。该方法是在倒谱预白化的基础上提出的。不同的是,该方法中实倒谱幅值的幂次是可变的。首先利用实倒谱和信号相位,得到修正信号,其表达式为
xm(t,p)=IFT(A(f)pejφ(f))
(1)
式中p为幅值幂次,取值范围[8]为-0.5≤p≤1.5。
A{xm(t,p)}=xm(t,p)+j*H{xm(t,p)}
(2)
SES{xm(t,p)}=|FT{|A{xm(t,p)}|2}|
(3)
式中:A[·]表示修正信号对应的解析信号;H[·]表示修正信号的希尔伯特变换;|·|表示取绝对值。通过式(3)求修正信号的平方包络谱。
此方法包含了两个主要步骤:
1) 通过设置不同范围的p值对信号产生不同的滤波效果。当1 2) 通过归一化平方包络谱降噪,提取具有较大振幅信号中的冲击特征。 假设传感器采集到的振动信号[11]为 x=h*y+e (4) 式中:h为传递函数;y为故障冲击序列;e为噪声。解卷积的目的是获得合适的滤波器对信号y进行滤波,最大程度恢复故障冲击相关成分。其原理简述如下: 首先,定义多点D-范数,即 (5) 式中目标向量t是用来定义解卷积目标冲击位置和权重的连续向量,该向量的大小与解卷积信号大小相同,冲击的位置和权重可分别通过其元素位置和大小来反映。该算法以多点D-范数最大化为目标,即 (6) 通过对滤波器组f求1阶导数的方式求式(6)的极值,同时假设(X0X0T)-1存在,最终可求得优化滤波器组f和输出结果分别为: (7) (8) 算法的详细介绍可参考文献[9],本文不再赘述。 SAM的优势在于通过调节幅值指数p可以非常灵活适应不同故障程度及类型的振动信号。但目前幅值指数p的取值需要人工根据谱幅值调制图综合各谐波的能量水平来判断,无法实现其对滚动轴承故障特征的自动优化提取。另一方面,在旋转机械故障诊断中,发展故障特征的自适应提取是实现故障诊断自动化的重要保障。 为实现SAM中幅值指数p的自适应选取,需要利用某一指标有效地反映信号中包含故障冲击成分的情况。常规的峭度指标易受信号中随机冲击噪声等因素的干扰[12];文献[13]提出的相关峭度较好克服了峭度易受随机冲击影响的缺点,但轴承故障产生的冲击在时域并非严格的周期信号而具有较强的2阶循环平稳性。因此,近年来2阶循环平稳指标(ICS2)被提出并在滚动轴承故障特征提取中取得较好效果。据此,本文选用ICS2作为幅值指数自适应的评价指标,其定义[10]为: (9) 式中:SESx(0)为高斯平稳信号;α为循环频率(预设为故障频率);MSx为信号x的均方功率;M为选取的故障特征谐波数。由于轴承存在滑移,因此该式中计算α时需要设置一个容错区间。研究表明,将该指标应用于式(1)计算所得的信号自适应获得幅值指数p可取得较好效果。 利用SAM技术可有效抑制无关周期信号的干扰,并提升故障冲击。但研究中发现,对于受时变传递路径影响的行星齿轮箱多源耦合信号,SAM并不直接适用(见本文图12),需要对信号进行前处理来增强故障冲击特征。 MOMEDA是一种较为理想的信号前处理方法,其优势主要包括两个方面:1) 以多点D-范数最大为目标进行求解可以有效降低随机冲击带来的影响;2) 采用非迭代方式求解滤波器,可以避免陷入局部最优解。总体而言,该方法通过获取周期冲击的全局最优解,可以有效增强故障冲击特征。基于上述分析,本文在对SAM进行改进的基础上,结合MOMEDA技术,提出鲁棒性幅值指数自适应谱幅值调制法。该方法的技术路线如图1所示。 图1 鲁棒性幅值指数自适应谱幅值调制法技术路线 基本步骤为: 1) 采集获得原始时域信号,通过等角度重采样得到角域信号,消除转速波动的影响。 2) 选取合适的滤波器长度L和周期点数范围,利用MOMEDA识别并提升角域信号中行星轴承内圈故障对应的微弱冲击特征。 3) 经过MOMEDA反卷积滤波后的信号作为SAM的输入信号,设定p值取值范围为[-0.5,1.5],研究中取步长为0.1,分别求修正信号。计算每个p值对应的修正信号的ICS2值,取故障特征谐波数M=3。输出其中最大的ICS2对应的p值,为优化p值。 4) 该优化p值自动输入SAM程序,得到其对应的归一化平方包络阶比谱,通过包络谱提取故障特征。 研究中用如图2所示的NGW型行星齿轮箱综合试验台验证本文方法的有效性。实验中使用RION PV-86 4527型加速度传感器(灵敏度:60.5 pC/g)及配套VM-27电荷放大器拾取振动信号;使用DH90型电涡流传感器(灵敏度:2.5 V/mm)获取转速信号。使用NI USB9234采集卡采集信号。 图2 行星齿轮箱综合试验台 传感器的具体安装位置如图3所示,其中电涡流传感器安装位置为图3中1处,加速度传感器共3个,安装位置分别为图3中2、3、4处。因位置3处的传感器采集的振动信号传递路径最短,本研究中使用该处采集的振动信号。 图3 传感器安装位置 行星轴承故障为电火花加工的人造故障,加工宽度约为1 mm,深度约为0.5 mm,用以模拟轴承局部故障,如图4所示。 图4 行星轴承内圈人造故障 行星齿轮箱1内所用行星轴承、齿轮参数分别如表1、表2所示。在输入端(对应太阳轮)转速为1 000 r/min时,以行星架为参考,利用表1和表2相关参数,由行星轮系的传动理论,计算得到的行星轴承内圈故障相关阶次如表3所示。 表1 行星轴承参数 表2 齿轮参数 表3 行星轴承内圈故障相关阶次 行星轴承内圈发生故障时,采集到的振动信号及实际转速曲线如图5所示,从图5中可以看出在该工况下,转速存在微小波动。为消除转速波动的影响,以行星架转轴为参考轴,对原始振动信号进行等角度重采样,将信号转换到角域。本文设置角域重采样率Fs=9 088点/r,为固定齿圈齿数的128倍。 图5 内圈故障行星轴承振动 等角度重采样后得到的原始角域信号如图6所示,其包络阶比谱如图7所示。 图6 角域信号 图7 内圈故障行星轴承振动的包络阶比谱 从图7中可见,太阳轮绝对旋转阶次ls(2.53×)、行星轮绝对旋转阶次lp(3.55×)和行星架旋转阶次lc(1.00×)相对突出,而行星轴承内圈故障特征阶次lbi(15.95×)完全被淹没。 直接使用MOMEDA识别并增强原始角域信号中行星轴承内圈故障冲击。计算得行星轴承故障理论周期点数为569. 8,其计算公式为 Tbi=Fs/lbi (10) 式中lbi为行星轴承内圈故障特征阶次。 为了减小与故障无关的信号干扰,应用MOMEDA技术时,周期点数范围应尽可能取小,但考虑到滚动轴承在工作过程中存在1%~2%的滑移[14],周期点数范围过小会导致故障信息利用不足。综合考虑,选取周期点数范围为(550,590),而滤波器长度L通常取在500到1 000范围内较为合适[15],本文取L=900。 图8所示为行星轴承内圈故障下振动信号经过MOMEDA冲击增强后的信号包络阶比谱。从图中可见,低阶次频段仍受到噪声干扰,难以有效获得故障特征信息,需要进一步对信号进行处理。 图8 内圈故障行星轴承振动的包络阶比谱 经过MOMEDA处理后的信号,复杂调制对故障冲击造成的影响难以被有效降低。后续经过SAM处理后的谱幅值调制图如图9所示。 图9 内圈故障行星轴承振动的谱幅值调制 图9中在1 图10 内圈故障行星轴承振动的ICS2曲线 利用ICS2优化SAM处理后得到的行星轴承内圈故障振动对应的信号平方包络阶比谱如图11所示。需要说明的是,因轴承滑移现象的存在,实际故障特征阶次与理论值存在约1.6%的偏差,但不影响故障特征提取。从图11中可见较为突出的行星轴承内圈故障特征阶次及其谐波,而无关周期信号被抑制,表明本文所提方法可以有效提取行星轴承故障信号的冲击特征。 图11 内圈故障行星轴承振动的平方包络阶比谱(p=1.3) 为说明利用MOMEDA对信号进行前处理的必要性,直接使用SAM对同一原始信号进行处理,结果如图12和图13所示。从图12中可见,当p在[-0.5,1.5] 范围变化时,齿轮啮合阶次及谐波始终占据主导地位,而行星轴承内圈故障特征不易观察到。进一步地,求特定p值时的平方包络谱。根据文献[8]中理论,在齿轮啮合信号干扰时,取p值在(-0.5,0)范围较为合适,本文取p=-0.3得到如图13所示的平方包络阶比谱,图中可见轴承故障特征被噪声淹没,难以读取有用的故障信息。结合图12和图13可知,直接通过SAM不易有效提取行星轴承故障特征。 图12 内圈故障行星轴承振动的谱幅值调制 图13 内圈故障行星轴承振动的平方包络阶比谱(p=-0.3) 本文针对SAM需要人工判断幅值指数p值,尚无法用其实现对故障特征的自动优化提取的不足,提出了鲁棒性幅值指数自适应谱幅值调制法,使用ICS2自适应地选取p值。结合MOMEDA可以有效增强故障冲击特征的优势,该方法先将MOMEDA技术用于故障振动信号的前处理,以增强故障冲击特征,再利用参数自适应SAM技术减小无关周期信号的干扰,提取故障特征。通过行星轴承内圈故障的实验,验证了本文方法的有效性。2 MOMEDA简介



3 鲁棒性幅值指数自适应谱幅值调制法


4 行星轴承内圈故障特征提取实验
4.1 实验简介





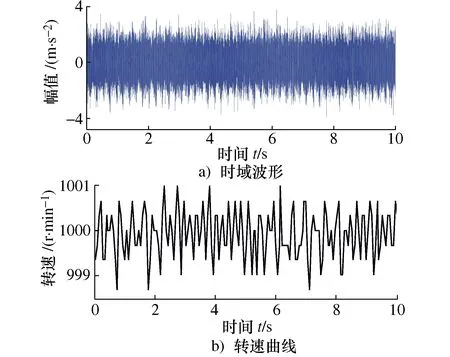
4.2 故障特征提取



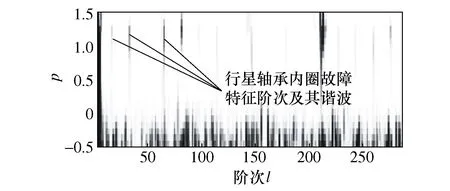


5 对比实验


6 结论

