应用ICEEMDAN和SVM的行星齿轮箱故障诊断

王浩楠, 崔宝珍, 彭智慧, 任川

(中北大学 机械工程学院,太原 030051)

行星齿轮箱具有结构紧凑、体积小、质量轻、传动比大、承载能力强、传动比高等优点,广泛应用于高速大功率以及低速大扭矩的机械传动场合[1]。由于在实际生产工作中,行星齿轮箱经常承受复杂的动态重载作用力,所以极易出现机械故障。齿轮故障是导致机械故障的主要因素,据调查显示在旋转机械故障中齿轮故障占总体的10%左右[2]。为了避免行星齿轮箱出现故障造成一些不必要的经济损失,以及出于对工作人员的生命安全考虑,国内外很多学者针对行星齿轮箱中的齿轮故障展开了深入的研究。

信号故障特征提取是故障诊断的前提。由于行星齿轮箱振动信号传输路径复杂、外界噪声干扰以及信号调制造成的多模式混淆,导致齿轮故障响应极其微弱。特别是行星齿轮箱运行时载荷的瞬时变化和齿轮故障,都会引起振动的非平稳性,更增加了故障诊断的难度[3]。

经验模态分解(Empirical mode decomposition，EMD)可以将信号分解成不同尺度的IMF分量,非常适用于非平稳信号,但由于存在模态混叠问题,分解效果不理想[4]。Torres等[5]提出了自适应噪声完备经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN),该方法通过自适应加入白噪声来放大模态之间的不相关程度,从而提取出原来不可分的两个模态。该方法能较好地解决模态混叠问题,重构信号中的噪声残余小,降低了筛选次数。Colominas等[6]提出了改进自适应噪声完备经验模式分解(Improved complete ensemble empirical mode decomposition with adaptive noise, ICEEMDAN),该方法通过改进在自适应分解中EMD分解的不足,大大减少了IMF中的残余分量,从而得到更好的重构结果,进一步改善模态混叠问题[7]。管一臣等[8]运用ICEEMDAN和频率解调对行星齿轮箱的电机电流信号进行分析,准确地提取行星齿轮箱的故障特征,实现了行星齿轮箱3种齿轮的故障诊断。姚瑞琦[9]利用ICEEMDAN的排列熵与SVM相结合,有效地改善了4种工况下的滚动轴承故障识别率。

针对行星齿轮箱复合故障难以分类的问题,本文利用ICEEMDAN和SVM对其进行故障识别。首先,将采集到的信号利用ICEEMDAN分解,得到不同尺度的IMF分量;然后,利用频域互相关剔除IMF虚假分量;最后,以优选IMF分量的多尺度模糊熵均值为特征向量,输入到SVM中进行分类得到最优的分类结果,并与传统方法进行对比,验证该方法的可行性和优越性。

1 信号特征提取方法

1.1 ICEEMDAN方法

传统的CEEMDAN的方法,在每次迭代中利用多个添加自适应噪声的原始信号或残余分量进行EMD分解得到多个IMF,并对其做平均处理得到最终的IMF。ICEEMDAN与CEEMDAN相比采用了上一步计算的残差与本次计算的多个添噪信号残差平均值的差作为本次迭代的IMF,可以进一步解决模态混叠问题,减少分解结果中的IMF虚假分量。

ICEEMDAN算法如下:

1) 在原始信号x的基础上构造N个含可控噪声的信号

x(i)=x+β0E1(w(i))i=1,2,…,N

(1)

式中：x(i)是第i个构造信号;β0是第一次分解时信号的噪声标准偏差;w(i)是第i个被添加的零均值单位方差白噪声;E1(·)是计算信号第一个IMF算子。

2) 对每一个x(i)计算局部均值并求平均,得到第一个残余分量为

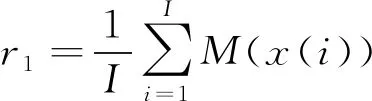
(2)

式中M1(·)为局部均值函数。

3) 计算第一个模态(k=1),原信号x减去第一次计算的残差r1，即

(3)

4) 计算第k个模态 (k≥2),将上一次计算的残差rk-1减去本次计算的残差rk,即

(4)

(5)

5) 计算第k=k+1个模态,返回第4步,直到满足迭代终止条件。

行星齿轮箱在正常工况时,一般呈现出一定的周期性。可以用低频或高频的简谐信号表示行星齿轮箱内部各构件的振动信号,用调制信号表示齿轮啮合故障点处的振动信号。假设行星齿轮箱的振动信号为:

(6)

利用CEEMDAN和ICEEMDAN分别对添加随机白噪声的X(t)进行分解,其中βk的取值范围一般为0.1～0.3,文中βk=0.2,噪声添加次数N=200[10]。

如图1所示,ICEEMDAN分解能够有效改善CEEMDAN分解产生的模态混叠和端点效应等问题,并且产生了较少的IMF无用分量。

图1 CEEMDAN与ICEEMDAN分解对比

1.2 频域互相关消除IMF虚假分量

ICEEMDAN分解过程中会不可避免地产生过分解,导致大量的低频分量出现。这些低频分量中大部分是虚假的IMF无法反映原始信号的特征信息,不仅增大了计算量而且会影响故障诊断的结果,所以剔除虚假分量是十分必要的。

由于虚假分量不能反映原始信号的特征,与原始信号的相关性差,所以可以将分解后的IMF分量与原始信号的互相关系数做为区分虚假分量的评定指标。传统的互相关分析一般在时域中进行互相关计算,并将互相关系数较小的IMF分量剔除。

在时域中,两个信号xi和yi的时域互相关系数ρxy可以描述为

(7)

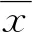
行星齿轮箱在实际运行中会产生大量噪声,由于噪声对时域信号影响严重,从而导致错误判断虚假分量。而在频域中,噪声虽然也存在于信号的各个频段,但有用信号的功率谱频率幅值远大于噪声在功率谱密度中的幅值,有用信号更加突出,进而抑制了噪声的干扰。

在频域中,用xi和yi的功率谱Gx和Gy替代xi和yi,fa是分析频率,频域互相关表示为

(8)

频域互相关与时域互相关相比,前者提取的IMF分量更真实。所以本文采用频域互相关来分析各阶IMF分量与原始信号的相关性大小,判断并剔除虚假分量[11]。

1.3 多尺度模糊熵

模糊熵是对时间序列在单一尺度上复杂性和无规则程度的度量。多尺度熵是对序列在不同尺度因子下的复杂性的度量。Costa等结合了模糊熵和多尺度熵的思想,提出了多尺度模糊熵的方法,能够在衡量时间序列在不同尺度因子下的复杂程度和维数变化时产生新信息的概率大小[12]。由于不同故障信号的不同特征频段的复杂度各不相同,因此可以用多尺度模糊熵作为信号的故障特征,区分不同类别的故障信号。

多尺度模糊熵算法如下:

1) 将IMF分量序列Xi={x1,x2,…,xN}粗粒化处理，则

(9)

式中τ=1,2,…,n为尺度因子。

2) 设置嵌入维度m,对粗粒化处理后的n个序列Yi(τ)={y1(τ),y2(τ),…,yN(τ)},构造m维向量

M(i)=[yi(τ),yi+1(τ),…,yj+m-1(τ)]-k

(10)

式中：i=1,2,…,N-m+1；k是连续m个yi(τ)的平均值。

3) 计算任意两个不同样本M(i)和M(j)之间的距离

(11)

4) 通过模糊函数,定义向量M(i)和M(j)的相似度

(12)

式中：n为模糊函数梯度；r为相似容限。

样本平均相似度函数

(13)

5) 设置维数m+1,重复步骤2)～步骤4),求φm+1(r);

6) 原始信号的模糊熵为

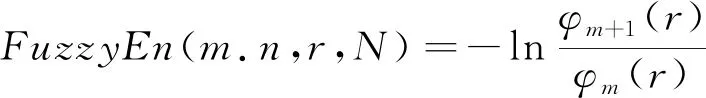
(14)

多尺度模糊熵在计算过程中,参数的选择是否合理,对计算结果有至关重要的影响。理论上讲嵌入维度m越大结果越精确,但m受数据长度的影响,一般取2或3;相似容限r决定模糊函数边界宽度,过大或过小都会导致统计结果不理想,一般取原始信号0.15倍标准差;模糊函数梯度n起权重作用,一般取2;数据长度N=10m～30m;本文中尺度因子取16[13]。

2 故障分类方法

支持向量机(Support vector machine, SVM)是一种基于统计学的一种机器学习方法。它通过结构风险最小化原则同时兼顾经验风险和置信范围,在小样本、非线性以及高维模式识别等问题中有明显的优势,能够在有限样本条件下,得到较好的分类结果[14]。

SVM是一种使用超平面作为分类函数的一种线性分类器。针对线性可分问题,应最大化超平面两边样本到超平面的距离之和,通过最大化分类间隔从而得到最优分类超平面。对于线性不可分问题,常常使用非线性映射算法将低维空间线性不可分转化为高维空间线性可分问题,在高维空间中对样本分类。但直接将特征从低维映射到高维,数据的计算量会非常庞大。在SVM中一般使用核函数来避免 “维度灾难”,核函数通过在低维空间进行计算将分类效果表现在高维上,从而避免了在高维空间的复杂计算[15]。

SVM的常用核函数包括:1) 线性核函数;2) 多项式核函数;3) 径向基核函数;4) 感知器核函数。本文使用径向基核函数来实现特征的分类。

3 ICEEMDAN-SVM故障诊断

本文使用HFXZ-I行星齿轮箱故障诊断试验平台,来验证该方法的可行性。试验平台的结构如图2所示,变频交流电动机为试验平台提供动力,磁粉离合制动器为行星齿轮箱提供负载。

图2 HFXZ-I行星齿轮箱故障诊断试验平台

设置故障工况:正常工况、太阳轮齿面磨损+行星轮两齿磨损、太阳轮齿面磨损+行星轮三齿磨损和太阳轮齿面磨损+行星轮齿面点蚀这4种工况。齿轮故障如图3所示。

图3 齿轮故障工况图

设置行星齿轮箱故障诊断试验平台。在负载电流0.3 A,变频交流电动机转动频率50 Hz条件下进行试验。在行星齿轮箱箱体输入轴和输出轴位置安装单向压电式加速度传感器如图4所示。设置传感器采样频率为10.24 kHz,通过数据采集器依次采集4种工况下的实验数据。

图4 传感器测点布置位置

3.1 信号的特征提取

选取行星架输出轴上的测点采集到的数据作为样本。并把4种工况的数据分别划分为80组样本信号,共320组数据,每组样本信号包含4 096个数据点。以行星齿轮箱正常工况为例,使用ICEEMDAN对样本信号进行分解。ICEEMDAN分解行星齿轮箱正常工况的IMF分量如图5所示。

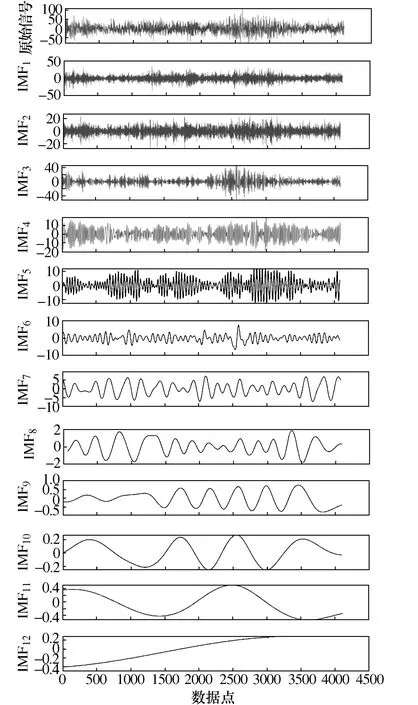
图5 行星齿轮箱正常工况ICEEMDAN分解结果

由于得到的IMF分量存在大量虚假分量,故采用频域互相关消除虚假分量。各IMF分量与原始信号的互相关系数如图6所示。根据图6选取第1、2、3、4、5、7阶互相关系数大于0.1的IMF作为特征分量。

图6 正常工况下各IMF分量的频域互相关系数

计算优选的IMF分量的多尺度模糊熵均值,尺度因子取16。每种工况80组样本信号,每组样本信号计算第1、2、3、4、5、7阶IMF分量的多尺度模糊熵均值。把4种工况总共320×6个数据,作为故障分类的特征，部分特征向量如表1所示。

表1 行星齿轮箱4种工况的部分特征向量

3.2 行星齿轮箱故障分类

将正常工况、太阳轮齿面磨损+行星轮两齿磨损、太阳轮齿面磨损+行星轮三齿磨损和太阳轮齿面磨损+行星轮齿面点蚀这4种工况的训练样本标签依次设置为1、2、3、4。在每种工况80组样本中选择60组数据共240组数据作为训练样本,每种工况剩余的20组数据共80组数据作为测试样本。由于篇幅所限,只列出每种工况下的5组信号样本的特征,如表1所示。

本文使用了由台湾大学林智仁教授等开发的LIBSVM工具箱进行SVM故障分类。SVM参数均设置为默认值:SVM参数类型s=0,核函数参数g=1/k(k为特征向量的维数6),错误惩罚因子c=1。核函数采用径向基核函数,其他参数均取默认值即可。

分别把用EMD、CEEMDAN和ICEEMDAN方法提取的特征矩阵输入到支持向量机中进行分类,并比较3种方法的分类准确率。得到的分类结果如图7～图9所示。

图7 EMD分解SVM分类预测图

图8 CEEMDAN分解SVM分类预测图

图9 ICEEMDAN分解SVM分类预测图

从图7可以看出使用EMD方法,SVM分类预测准确率为90%。其中正常工况和太阳轮齿面磨损+行星轮齿面点蚀故障工况中有8组样本错分。

从图8可以看出使用CEEMDAN方法,SVM分类预测准确率为95%。其中太阳轮齿面磨损+行星轮齿面点蚀和太阳轮齿面磨损+行星轮三齿磨损故障工况中有4组样本错分。

根据图9可知使用ICEEMDAN方法,SVM分类预测准确率达到了100%。

表2对比了3种方法的分类准确率,并计算对应方法下每种工况提取80组特征向量的耗时。通过表2可以得出使用ICEEMDAN和SVM相结合的方法可以很好地兼顾分类准确率和计算耗时,能够更准确快速地解决行星齿轮箱的复合故障分类问题,证明了该方法的可行性和优越性。

表2 3种方法分类对比

4 结束语

本文针对行星齿轮箱的复合故障准确分类问题,应用了ICEEMDAN和SVM相结合的方法实现了行星齿轮箱的故障诊断。利用ICEEMDAN方法对不同工况信号分解,改善了CEEMDAN方法造成的模态混叠和无用分量过多等问题。最后使用SVM对行星齿轮箱的4种工况进行分类,通过对比3种方法的分类准确率,证明了该方法对行星齿轮箱复合故障分类的可行性和优越性。