定-变速抽水蓄能机组调相-发电过渡过程动态特性研究

陈帝伊，刘公成，梁 潇，邓宇闻，胡匡清，许贝贝

(西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)

1 研究背景

常见的抽水蓄能电站分为采用同步电机的常规抽水蓄能电站和采用双馈异步交流电机的可变速抽水蓄能电站。截止目前，我国绝大多数投运的抽水蓄能电站均采用定速机组，对变速抽水蓄能电站的研究与应用较少[1]。相较于定速机组，可变速抽水蓄能机组运行稳定性好、效率高，功率调节性能好[2]，具有更好的调相调频能力，能够充分发挥对间歇性可再生能源的协调控制功能，有效提高可再生能源的消纳水平[3-4]，对提升电网电能质量具有重要意义[5]。

抽水蓄能机组既能运行于水轮机工况又可在水泵工况运行，具有很强的灵活性，可变速机组的工况相对于常规蓄能机组更为繁多，不同工况之间的转化类型达34种之多[6]，不同工况之间的转换也更为复杂。而调相-发电过渡过程作为抽水蓄能机组应对风光等间歇性可再生能源波动的典型过程，机组过流部件压力及系统运行稳定性都会受到影响。因此，从理论层面深入分析调相-发电过程中相关水力动态特性对抽水蓄能机组、电站以及电力系统的稳定安全运行具有重要的学科意义和工程价值。

调相(包括发电调相和抽水调相)工况在工况转换中扮演重要角色，对平衡电网无功与调节电压意义重大，是一个不可或缺的环节。国内外学者对调相转发电及其他工况转换过程进行了大量研究，Zhao等[7]分析了常规抽水蓄能机组在发电调相转发电的过程中不同切换时间及两种导叶开启方式(直线/指数)对机组动态特性的影响。姜海军等[8]考虑到全特性曲线中不稳定区域的存在可能会导致工况转换失败，根据机组水力特性对切换过程及控制流程进行优化以尽量避开不稳定运行区。付婧等[9]针对无叶区压力脉动引起的机组及厂房振动，利用傅里叶方法对调相转发电等工况转换过程中无叶区的压力特性进行分析并得到压力脉动的变化规律。Riasi等[10]采用特征法对电站流道瞬态水流动力学进行了研究并验证了溢流阀的有效性。现有文献对由调相转发电的工况转换过程的研究主要以传统的常规抽水蓄能机组为研究对象，对可变速抽水蓄能机组参与工况转换过程的研究相对较少。抽蓄机组的一管双机布置可以有效节约电站建设成本，在已建和在建的抽蓄电站中广为采用。但这种布置形式存在水力干扰现象，变速机组引入后，其与定速机组之间的调节性能差异会使机组的水力特性指标展现出不同于传统机组的动态特性。

综上，本文利用模块化建模方法，搭建出综合考虑水力、机械、电气因素耦合的定、变速抽水蓄能机组整体精细化仿真模型。基于抽水蓄能机组调相转发电运行的工况转换过程，深入探究不同机组组合形式在该过程下压力、流量等水力特性的动态变化规律。

2 一管双机定-变速抽蓄机组模型

本文利用双馈异步电机、网侧及机侧变流器的数学模型搭建出可变速抽水蓄能机组电气子系统仿真模型。同时，从系统科学的角度出发，与机组机械子系统、引水系统和控制系统的数学模型进行耦联，如图1所示[11]，依托MATLAB/Simulink平台建立考虑水、机、电耦合因素的可变速抽水蓄能机组整体仿真模型。

图1 定-变速抽水蓄能电站结构简图

2.1 引水系统建模

2.1.1 特征线法基本方程 运用特征线法将描述管道非恒定流的偏微分方程进行转化以实现数值计算。如图2所示，RP为正特征线C+，斜率为a；SP为负特征线C-，斜率为-a。

图2 特征线网络示意图

特征线方程经沿各特征线积分、整理化简后成如下形式[10]：

C+：HPi=CP-BPQPi，C-：HPi=CM+BMQPi

(1)

式中：QPi和HPi分别为t时刻管道内P点的流量和水头；CP、BP、CM、BM为运算时的中间变量，其表达式为

(2)

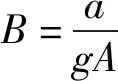
2.1.2 管道边界数学模型 特征线法计算时，管道中间网格点同时满足式(1)，各点Q和H可直接求出。管道连接处、分叉端、上下游和特定建筑物处一般只满足一个特征线方程，需补充边界条件进行求解，主要边界包括上下游水库调压井和分岔管。在整个工况转化过程中假设水库上、下游水头恒定不变，即：HP1=Hres上，HP2=Hres下。式中Hres上、Hres下为上、下游水位，HP1、HP2为管道进、出口处测压管水头。根据图3将上下游水位分别代入式(1)中的C-、C+，可分别求得管道进、出口流量QP1和QP2。

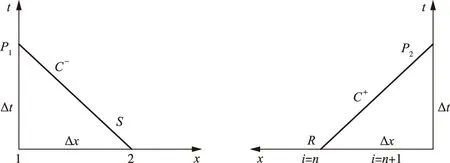
图3 上、下游边界特征线示意图

(3)

其他边界处理方式如图4所示，岔管的主管与分岔管压力相等，主管流量为分岔管流量之和；调压井流量为调压井前，后段流量之差；“1”处满足正特征线方程，“2”处满足负特征线方程，公共点处压力相等。具体方程参考文献[12]。

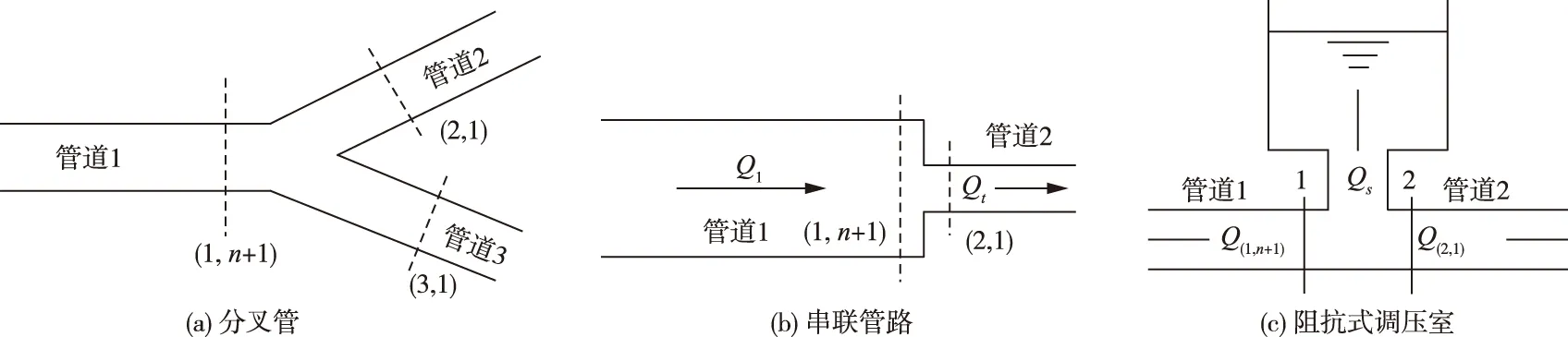
图4 引水系统边界特征线示意图

2.2 双馈电机及控制系统建模采用等幅值的原则将三相静止坐标系下动态模型转化成两相旋转d-q坐标(3s/2r)如图5所示，则两相d-q坐标下电机的数学模型为[13]。

图5 双馈电机同步旋转d-q坐标系

(1)电压方程组

(4)

式中：usd、usq、urd、urq为定转子的d、q轴电压分量；isd、isq、ird、irq为定转子的d、q轴电流分量；φsd、φsq、φrd、φrq为定转子的d、q轴磁链分量；ωs、ωr分别为同步转速角速度和电机转子角速度。

(2)磁链方程组

(5)

式中：Lm为等效转子绕组互感；Ls为等效定子绕组自感；Lr为等效转子绕组自感。

(3)转矩方程

(6)

式中np为磁极对数。

(4)运动方程[14]

(7)

式中：J为转动惯量；Tm为机械转矩；D为阻尼系数。

基于两相d-q坐标体系下双馈异步电机定子端输出有功功率Ps和无功功率Qs的计算表达式为[15]：

(8)

转子侧变流器控制系统的控制策略为外环功率控制系统(图6(a))输出的转子电流参考值输入到内环电流控制系统并将电流信号转化为转子侧电压的d、q轴分量(图6(b)(c))，进而调整定子侧有功和无功比例以改变机组功率(其中ω2、ωg分别为电机转子角频率和电网电压角频率)。

图6 转子侧变流器内、外环控制系统

网侧变流器的控制策略为电压参考值Udref与反馈电压Ud作差后经PI控制器得到电流参考值igdref，igdref与反馈电流igd作差后通过PI控制器得到输出电压并与扰动补偿项作差得到电压参考值Ugdref，结果输入到空间矢量脉宽调制(SVPWM)最终实现对网侧变流器的控制。网侧变流器的矢量控制系统如图7所示：

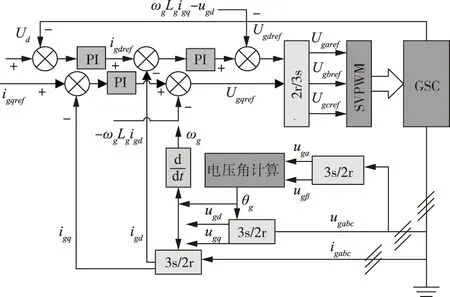
图7 网侧变流器矢量控制系统

水轮机调速器采用PI型控制调节，由PI控制器与执行机构(液压随动系统)构成，可用下述微分方程描述：

(9)

式中：Kp2、Ki2分别为PID调速器的比例和积分系数；bp为永态转差系数；Δωr为转速的相对偏差值；Δy为导叶开度的相对偏差值。

2.3 一管双机定-变速机组整体仿真模型将以上各子系统转换为MATLAB/Simulink中的S函数，经模块化组合得到一管双机定-变速机组的整体精细化仿真模型如图8所示，其中引水系统的输入为两机组的转速Wr与导叶开度y，通过特征线法输出转矩Tm，调速器的输入为机械转矩Tm与电磁转矩Te，进而控制机组的转速Wr(定速机组时为常数)和导叶开度y，下标1、2代表一管双机布置时机组编号，机组输出的电能与电力系统模块连接并入电网，替换相应定变速机组模块即可实现定速-定速、定速-变速、变速-变速三种不同布置形式的模拟。

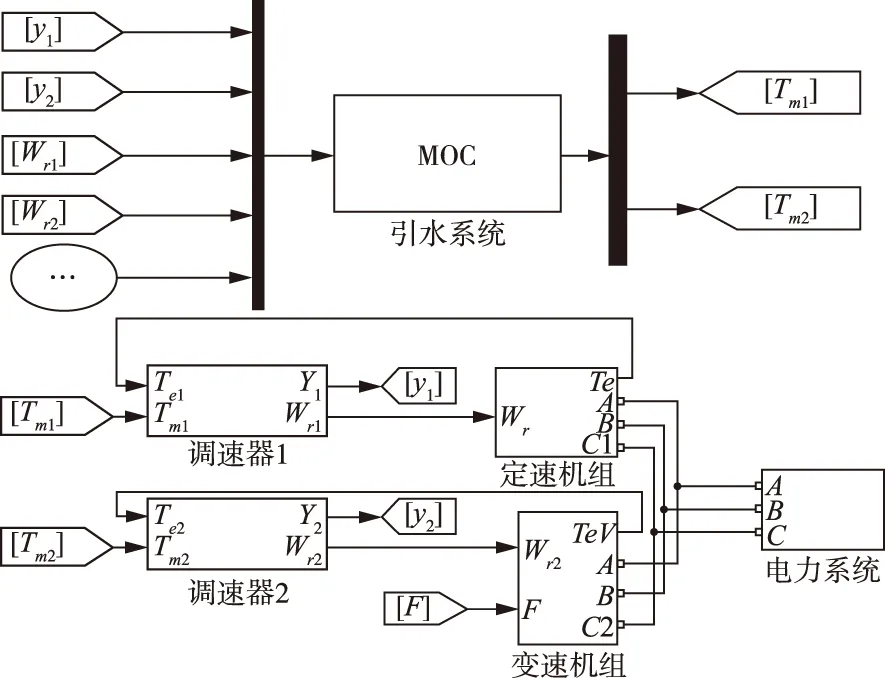
图8 定-变速布置形式下抽水蓄能机组整体精细化仿真模型

3 结果与分析

3.1 仿真工况与参数本文选取某实际抽水蓄能电站为参照，其结构简图如图9所示，表1为整体模型的各参数取值。

图9 抽水蓄能电站结构简图

表1 整体仿真模型参数取值

水泵水轮机需作为管道的边界进行计算，基于其全特性曲线，通过S函数实现引水子系统、水泵水轮机子系统在Simulink模型中的组合，同时结合发电机模型以实现水力子系统、机械子系统和电气子系统的相互耦合。图10为本文参照建模的抽水蓄能电站机组的全特性曲线，其中，N11、Q11和M11分别为单位转速、单位流量和单位力矩。

图10 水泵水轮机全特性曲线

由于水泵水轮机的全特性曲线在部分区域存在多值问题，通过式(10)中的改进Suter变换[16]对原曲线进行了处理以消除多值导致的精度问题。

(10)

式中：xs为相对流动角；Wh(x，y)和Wm(x，y)分别为无量纲流量参数和无量纲转矩参数；h、n、q、y分别为水头、转速、流量与导叶开度的相对值[17]，经过变换后的全特性曲线如图11所示。

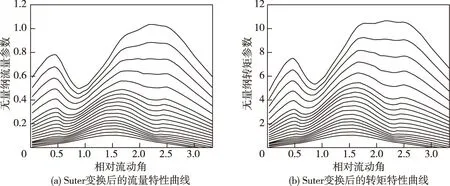
图11 改进Suter变换后的流量、转矩特性曲线

抽水蓄能机组由发电调相转发电工况切换过渡过程[18]的全流程如图12所示。

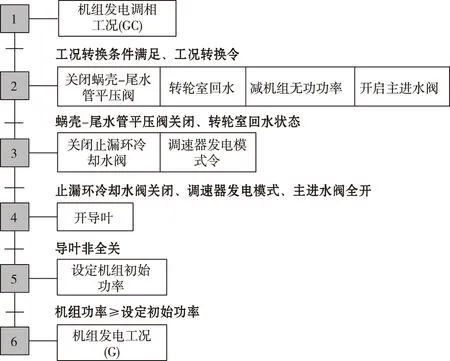
图12 调相-发电过渡过程流程

机组在调相-发电过渡过程需接入频率稳定的大电网，传统定速机组的机组转速与电网频率直接相关，并网运行时转速基本不发生变化。而变速机组由于转速与输出功率解耦，转速会在一定范围内波动。图13(a)(b)为变速-变速组合时机组的相对转速(实际转速/额定转速)，图13(c)为定速-变速组合时机组的相对转速。根据图13可以发现，转速变化更多的是受时间延迟的影响，相比于转速的变化，一管两机布置形式下的水力干扰现象导致水力特性指标存在明显的波动，因此本文主要针对机组的水力特性进行详细分析。

图13 不同机组布置形式下变速机组的转速特性

3.2 定速-定速机组动态特性定速机组1经30 s转换至带满负荷状态，机组2的开启时间分别设置为机组1开启后5、10、15、20、25 s，仿真时间设定为180 s。图14分别展示了在不同间隔时间下由调相转发电过程中两机组工作水头、蜗壳压力、尾水压力、调压井水位及流量的动态特性。

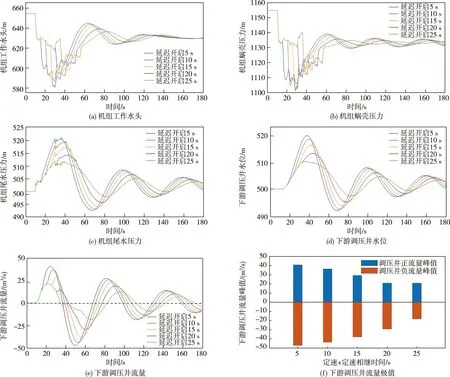
图14 定速-定速布置形式下机组水力动态特性

从图14中可看出，定速机组调相转发电过程中，机组工作水头、蜗壳压力在经历较大程度下降后波动上升并最终趋于稳定，机组尾水压力、下游调压井水位及流量具有正弦式衰减振荡的特征。在图14(a)(b)中，机组工作水头和蜗壳压力在0～40 s出现两段较为明显的下降，工作水头由655 m降至582 m，蜗壳压力由1155 m最低降至1102 m。随着两机组动作间隔时间由5 s增加到25 s，水头和压力下降的间隔时间相应延长。无论间隔时间取何值，两机组工作水头和蜗壳压力最终均稳定于630.6 m和1134.4 m，故不同动作间隔时间对水头和压力在该过渡过程的末值基本没有影响。从图14(c)(d)中可以看出，机组尾水压力在20～60 s内的第一个波峰过程中出现小范围的振荡，随着动作间隔时间由5 s增大到25 s，机组最大尾水压力由521.1 m降低到511.5 m，下游调压井水位最大值由519.8 m降低到510.2 m，故延长两机组动作间隔时间有效减轻了尾水压力和调压井水位的振荡幅度，该过渡过程结束后两者最终稳定至与下游水位相等的500 m。

表2和图14(f)定量展示了机组不同动作时间间隔下工作水头、蜗壳压力、尾水压力、调压井水位及流量的极值，可以发现延长两台机组的动作间隔时间能在一定程度上减小机组压力的变化幅值，有效减轻水压力在该过渡过程中对机组过流部件的冲击。

表2 定速-定速布置形式下机组参数极值

3.3 定速-变速机组动态特性与前述分析类似，变速机组相对定速机组动作间隔时间分别取5、10、15、20、25 s，仿真时间仍为180 s。图15分别展示了在此过程中定速-变速机组由调相转发电过程中机组工作水头、蜗壳压力、尾水压力、调压井水位及流量的动态特性。

从图15(a)(b)可以看出，定速-变速形式在工况转换过程中工作水头和蜗壳压力的下降呈现阶梯式降低，与定速-定速机组布置形式相比更为平缓。5种不同动作间隔时间下的机组工作水头最低值分别为579.1、593、596.5、603.4、607.9 m，工作水头最大值分别为644.9、642.8、639.6、636.7、635.9 m，由表3和图15(f)可以看出，工作水头、蜗壳压力的波动幅值较定速-定速机组均有所降低。不同动作间隔时间下机组尾水压力、下游调压井水位及流量的振幅相比定速-定速布置也均有减小。

表3 定速-变速布置形式下机组参数极值

图15 定速-变速布置形式下机组水力动态特性

3.4 变速-变速机组动态特性变速-变速机组布置形式下的水力特性响应整体与定速-变速布置的响应类似(见图16)，但机组工作水头和蜗壳压力在初始下降以及之后的上升过程中出现了明显的局部振荡。值得注意的是，在相继时间为5 s时，工作水头和蜗壳压力的波动峰值分别超过了其初值655 m和1155 m，该布置形式下两参数衰减振荡的起始时间在100 s左右，相比于定速-变速布置形式的起始时间有所滞后。尾水压力在20～100 s内有明显的局部小幅振荡，而定速-变速布置形式中尾水压力的局部小幅振荡仅出现在20～80 s内的波峰中，即变速-变速布置下尾水压力的局部振荡时间延长，振荡出现在第一个波峰和第一个波谷处且波峰处尤为明显。下游调压井水位及流量波动幅度较定速-变速布置也有所增大，变速-变速布置形式下的下游调压井流量正峰值并未出现在第一波峰，而是出现在95～105 s内的第二波峰处。

图16 变速-变速布置形式下机组水力动态特性

为了定量刻画出不同布置形式下相应水头、压力等波动范围的缩小程度，表5统计了三种不同布置形式的机组在不同动作间隔时间下水力特性的波动率，机组工作水头和蜗壳压力的基准值分别为其稳定值630.6 m和1134.4 m，尾水压力和下游调压井水位基准值为其稳定后的下游尾水位500 m，下游调压井流量基准值选定为300 m3/s。由表5可知，在不同的动作间隔下，除间隔5 s时的工作水头和蜗壳压力外，定速-变速的机组布置形式相较于定速-定速布置能在一定程度上减小压力、水位及流量的暂态波动幅值。不同动作间隔下，调压井水位、尾水压力、工作水头、蜗壳压力及调压井流量波动率的最大降低值分别为0.98%、0.90%、1.82%、1.00%、7.22%，最大降低率均出现在机组动作间隔时间为15 s时。较定速-变速机组和定速-定速机组而言，变速-变速机组布置形式下各指标的暂态波动幅值均有所增大，与定速-变速相比调压井水位及尾水压力波动幅值约增大1.5%，机组工作水头、蜗壳压力和调压井流量波动幅值的最大差距分别为7.22%、3.82%和11.32%。与定速-定速布置相比，调压井水位及尾水压力波动率的增长幅度小于1%，但工作水头、蜗壳压力和调压井流量波动幅值的最大偏差分别为7.60%、4.06%和4.10%。以上定量分析表明，一管双机布置形式时，变速-变速机组合形式在调相转发电的暂态过渡过程中的机组水头、压力、流量等水力特性的不稳定性相较于其他布置形式均有所增大。

表4 变速-变速布置形式下机组参数极值

表5 不同机组布置形式下水力特性的波动率 (单位： %)

续表5 不同机组布置形式下水力特性的波动率

4 结论

本文选取抽水蓄能电站由发电调相转换至发电工况的暂态过渡过程为背景，探究了机组在三种不同布置形式下相应水力指标的动态特性。具体研究内容可分为以下三部分：1)基于MATLAB/Simulink，利用特征线法和模块化建模方法搭建起一管双机三种不同布置形式(定-定、定-变、变-变)的整体精细化仿真模型；2)分别对三种不同布置形式下机组的工作水头、蜗壳压力、尾水压力、下游调压井水位及流量等水力指标的动态响应进行模拟，探究不同动作间隔时间下机组的动态特性；3)对三种机组布置形式下水力指标的动态响应极值和波动范围进行量化和对比分析；具体结论如下：

本文选用的特征线-机组模型精细化组合的方法较好的将引水系统与定-变速机组进行耦合，有效模拟了抽蓄机组在一管双机布置形式下存在的水力干扰现象。能够较好的体现出变速机组与定速机组之间的调节性能差异，引入变速机组后，系统的动态特性指标展现出不同于传统定速-定速布置的现象。

在调相转发电过程中，三种不同机组布置形式下的水力特性演变趋势总体相似，其中工作水头及蜗壳压力先下降后上升并最终趋于稳定，尾水压力、下游调压井水位及流量呈正弦式衰减振荡。延长两机组动作间隔能减小水力特性的波动幅值，但过长的间隔会影响机组响应速度，对电能质量不利。

两台机组相继动作的过程中，定速-变速布置的水力波动幅值较小，变速-变速布置的水力特性波动相较于定速-定速与定速-变速布置均有所增大。即在一定动作间隔范围内，变速-变速机组布置在该过渡过程中的水力特性波动幅度最大。因此，针对传统定速-定速布置的的调保计算结果仍可以保障定速-变速布置形式机组的安全运行，但对于变速-变速布置则需考虑机组类型对电站水力特性的影响。