科氏振动陀螺全角模式阻尼误差与补偿
樊 琦,潘覃毅,陈家伟,赵万良,成宇翔
(1.上海航天控制技术研究所,上海 201109;2.上海惯性工程技术中心,上海 201109)
科氏振动陀螺是一种利用科氏效应敏感基座相对惯性空间旋转角速率或角度的惯性传感器。根据工作模式的不同,科氏振动陀螺可分为角速率陀螺[1]和全角陀螺[2-4]。其中角速率陀螺将谐振子的一个工作模态激励至稳定的幅度,当陀螺旋转时利用另一个工作模态的位移输出或抑制该位移的反馈力表征角速率的大小。而全角陀螺同时激励谐振子两个工作模态,产生自由进动的驻波,当陀螺旋转时驻波能量在两个工作模态上重新分配,根据驻波方位角表征基座旋转的角度。相对于角速率陀螺,全角陀螺具有直接输出角度信息、大动态范围、高测量带宽及稳定的标度因数等优势,因此受到国内外科研工作者的关注。
但是高性能全角陀螺对谐振子刚度对称性、极板间距一致性、阻尼对称性及检测电路增益一致性有严格要求。英国纽卡斯特大学团队提出利用扩展卡尔曼滤波方案[5]对全角陀螺模态增益误差参数进行离线处理,降低了因极板间距误差、检测电路增益误差等因素引起的角速率漂移。美国加州大学欧文分校团队针对全角陀螺增益误差提出开环扫频法进行参数确定及补偿[6]。增益误差自校准[7]及单路复用法[8]可实时消除全角陀螺的增益误差。英国纽卡斯特大学团队针对全角陀螺刚度非对称提出利用粗调和精调模态频率调谐方案[9],将频率降低至10 mHz。南京理工大学团队提出一种利用虚拟旋转进行实时频率匹配的方案[11],将角度输出误差在全温范围从6.1 °降低至1 °。上海航天控制技术研究所团队在主轴失准条件下,对半球谐振陀螺进行了电刚度补偿[11]。目前针对全角陀螺阻尼误差的相关研究相对缺乏,阻尼误差是通过工作模态间的振动速度进行耦合,而科氏效应也是基于工作模态间的振动速度进行驻波能量的转化,因此阻尼误差很难与科氏效应进行区分。Horsley 等人针对阻尼误差提出了电学反馈补偿方案[12],对能量分布矩阵进行了差异化调整,将角度输出误差降低了30 倍。中国国防科技大学团队提出基于阻热消散法对陀螺的非对称阻尼进行了抑制[13],并应用在全角陀螺中,实验结果表明非对称阻尼降低了87%。苏州大学团队基于傅里叶拟合技术及多次迭代技术[14],对MEMS 蜘蛛网状陀螺误差参数进行辨识,经补偿后的最小速率阈值为0.05 °/s。但以上研究成果表明,目前全角陀螺阻尼误差抑制主要是通过虚拟旋转以及对阻尼误差的离线辨识,但缺乏有效的自动阻尼误差补偿方案。
本文针对全角陀螺的阻尼误差,提出在阻尼主轴坐标系中采用能量衰减法对阻尼误差的影响进行研究,确定了全角陀螺的速率死区指标,并得到了在不同外界角速率下全角陀螺的进动特性。提出全角陀螺自适应阻尼补偿方案,建立了Simulink 模型并仿真验证了方案的有效性。最终实验结果表明,采用自适应阻尼补偿法对全角陀螺阻尼误差进行抑制,将MEMS多环陀螺的速率漂移从2 °/s 降低至0.25 °/s,性能提高了8 倍。
1 能量衰减法及全角陀螺速率死区
目前,国内外大多数全角陀螺控制方案及角度误差研究都是基于D.D.Lynch 的平均法,有关公式及定义可参考文献[15],在此不再赘述。我们利用旋转矩阵对全角陀螺阻尼误差矩阵进行研究,提出利用能量衰减法确定阻尼误差对全角陀螺驻波进动的影响,并确定了阻尼误差引起的速率死区。
全角陀螺阻尼误差模型如图1 所示,其阻尼主轴所在坐标系为x1-y1,陀螺两工作模态阻尼系数分别为c1和c2,阻尼系数的不同将导致驻波能量在陀螺两个工作模态上的衰减速率不同,此坐标系下陀螺的阻尼矩阵C' 如式(1)所示。

图1 全角陀螺阻尼误差模型Fig.1 The damping error model of the WA gyro

而x-y坐标系是陀螺驱动、检测电极所在位置,由于与坐标系x1-y1之间相差角度β,因此导致陀螺两个工作模态间存在能量耦合,干扰科氏效应引起的驻波能量耦合。由于阻尼误差引起的驻波能量耦合与科氏效应引起的驻波能量耦合相位一致,因此很难将二者进行区分,加大了阻尼误差补偿的难度。
利用如式(2)所示的旋转矩阵R,用于x-y 坐标系下阻尼矩阵C及x1-y1坐标系下阻尼矩阵C' 的互相转换,坐标旋转过程如式(3)所示。

最终得到x-y 坐标系下陀螺的阻尼矩阵C为:

根据式(4),阻尼矩阵中的对角元cxx和cyy引起全角陀螺两轴振动幅值的衰减,而非对角元cxy和cyx引起全角陀螺两轴之间能量的耦合。
即使陀螺阻尼主轴所在坐标系与激励、检测电极所在坐标系不重合,采用式(2)及式(3),可以将阻尼矩阵C转换为阻尼矩阵C',即在陀螺阻尼主轴坐标系下研究陀螺驻波进动特性,这样可以不考虑两阻尼轴之间的阻尼耦合。在该坐标系下,陀螺两个工作模态的振动位移x1(t)、y1(t)分别为:

其中A为驻波的幅值,θin是驻波相对阻尼主轴的初始角度,τx和τy分别是阻尼轴x1、y1的自由衰减时间常数。
当陀螺两个工作模态的阻尼不相等时,即τx≠τy,驻波能量在x1、y1轴上的衰减速度不同,因此导致驻波方位角的漂移,如式(6)所示。
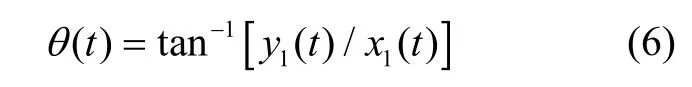
对式(6)相对于时间进行微分,可以得到驻波漂移速率:
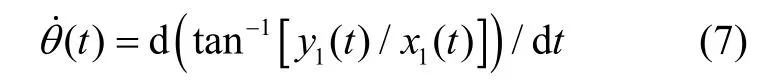
并将式(5)带入式(7)中,便可以得到驻波漂移速率关于驻波方位角θ的函数,如式(8)所示。

其中 Δ(1/)τ是陀螺两个工作模态之间的阻尼误差:
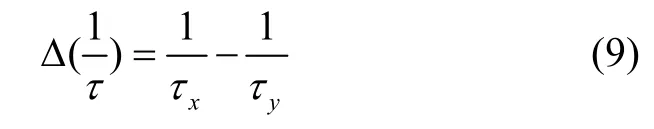
由于式(8)中,驻波的漂移速率是在阻尼主轴所在坐标系中求得,考虑阻尼主轴坐标系与陀螺激励、检测电极坐标系之间的角度β,并考虑标度因数κ的作用,根据能量衰减法得到驻波受到阻尼误差的影响在电极坐标系下的漂移速率,如式(10)所示。

根据式(10),得到全角陀螺受到阻尼误差导致的速率死区,如式(11)所示,即陀螺若想工作于全角模式下,必须突破该速率死区Ωth的限制。
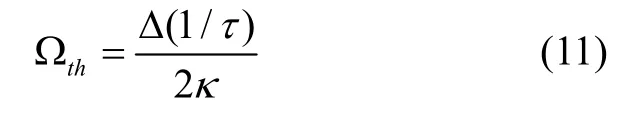
2 阻尼误差对全角陀螺驻波进动的影响
(1)Ω=0 时
为了验证阻尼误差对驻波方位角漂移的影响,令τx=1s 且τy=2s,当无外界角速率输入时,不同初始方位角驻波的漂移如图2 所示。
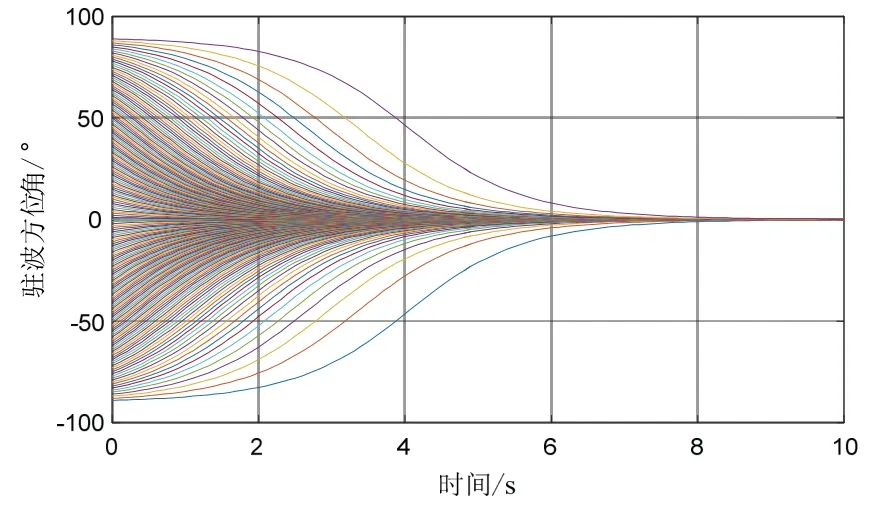
图2 陀螺驻波受阻尼误差影响产生漂移Fig.2 Gyro standing wave drift due to damping error
由图2 可以发现,由于陀螺两个工作模态存在阻尼误差,初始方位角不同的驻波最终都漂移至陀螺阻尼主轴。
为了研究不同阻尼误差大小对陀螺驻波漂移的影响,设置τx=1s,而τy比τx大10%~100%,驻波初始方位角为89 °,驻波漂移如图3 所示。

图3 陀螺驻波受不同阻尼误差影响产生漂移Fig.3 Gyro standing wave drift under different damping errors
由图3 可以发现,陀螺阻尼误差的大小影响驻波漂移的速率,且阻尼误差越大,驻波漂移至阻尼主轴所用时间越短,即驻波漂移的速度越快。
设置陀螺谐振频率为8800 Hz,陀螺的品质因数Qx=40000,Qy=30000,在陀螺阻尼主轴坐标系中,在不同方位角下驻波受阻尼误差产生的漂移如图4 所示,其中最大漂移速率发生在45 °,为6.6 °/s,该驻波最大漂移速率便是由于阻尼误差导致的速率死区Ωth。
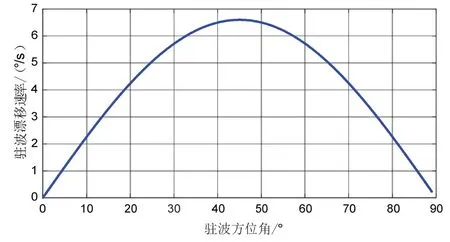
图4 陀螺驻波在不同位置处的漂移速率Fig.4 Gyro standing wave drift at different positions
因此当外界没有角速率输入时,陀螺的驻波便朝着阻尼主轴进行漂移,并停留在该轴所在方位角。
(2)0<Ω≤Ωth时
当外界角速率输入大于零而小于速率死区Ωth时,驻波虽然可以产生进动,当进动到某一方位角,且在该方位角驻波的漂移速率与外界角速率产生的驻波进动速率相等时,驻波便停留在此位置,不再进动。此时陀螺无法工作于全角模式下。
当只考虑阻尼误差对驻波进动的影响,当驻波无法进动时,驻波的进动速率为零,即=0,带入式(10)即可得到此时驻波所在方位角θlock。

设置阻尼误差引起的速率死区 0.5×Δ(1/τ)=15 °/s,角度增益为κ=0.8,阻尼主轴方位角β=0,当外界角速率Ω为1 °/s、5 °/s、10 °/s和15 °/s 时,陀螺驻波产生的进动如图5 所示。
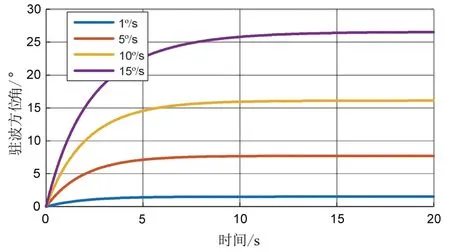
图5 陀螺驻波未突破速率死区在不同角速率下的进动Fig.5 Precession of gyro standing wave at different angular rates without breaking through rate dead zone
由图5 可知,当外界角速率输入小于陀螺速率死区时,驻波能够离开阻尼主轴产生进动,然而由于无法突破速率死区的限制,最终驻波被锁定在对应的方位角,且此时由于阻尼误差产生的驻波漂移与外界角速率相抵消。因此陀螺若想工作于全角模式下,必须突破速率死区的限制。
(3)Ω>Ωth时
当外界角速率输入大于此速率死区,且假设陀螺不受增益误差及刚度误差的影响,驻波便可以突破速率死区的限制,工作于全角模式下。然而陀螺驻波进动速率-κΩ还是受到阻尼误差周期性的干扰,只有当κΩ≫0.5×Δ(1/τ)时,驻波进动速率所受干扰才可以忽略。
外界角速率输入突破速率死区限制后,陀螺便可以直接输出驻波方位角,将陀螺的理想输出θ=κΩt代入式(10),得到:

将式(13)相对于时间进行积分,便可以得到陀螺的角度输出,如式(14)所示。

因此从式(14)可以发现,全角陀螺虽然完成了对角速率输入的积分,得到了角度输出-κtΩ,但是该角度输出受到周期性角度误差的干扰,此周期性角度误差幅值即为全角陀螺的角度分辨率θdamping:

设置外界角速率输入为Ω=40 °/s,阻尼误差导致的速率死区为18.75 °/s,角度增益κ=0.8,陀螺的角度输出在理想条件和非理想条件下如图6(a)所示,非理想条件下的角度输出误差如图6(b)所示。

图6 陀螺驻波在非理想及理想条件下的进动Fig.6 Precession of gyro standing wave under non-ideal and ideal conditions
从式(15)可以发现,阻尼误差导致的陀螺角度输出误差与角速率输入成反比关系,角速率输入越大,陀螺角度输出误差越小,如图7 所示,说明全角陀螺更擅长于检测大角速率输入。

图7 全角陀螺角度输出误差与输入角速率的关系Fig.7 Relationship between angle output error and input angular rate of WA gyro
从式(15)可以看出增大外界输入角速率的好处,因此可以在实际角速率输入Ωin上叠加已知的虚拟角速率Ωvir,使总角速率输入Ωtotal满足:

这样即便角速率Ωin<Δ(1/τ)/2κ,此时也可以进行全角工作模式,最终只需要在陀螺的最终角度输出减去虚拟角速率输入部分便可。
3 自适应阻尼补偿
速率死区是全角陀螺的一个重要性能指标,当陀螺只受到阻尼误差的干扰,其角度输出如式(17)所示。
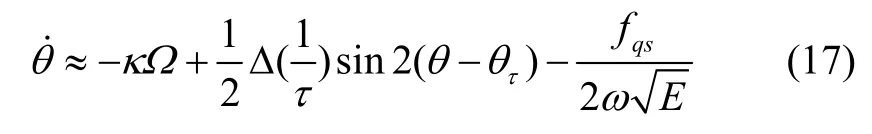
其中fqs可用于产生虚拟转速,当其满足式(18)时,便可以消除阻尼误差引起的驻波方位角的漂移。
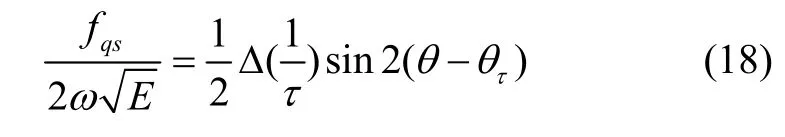
因此需要对陀螺的角度输出信号中的阻尼误差项进行自适应参数辨识,以产生所需虚拟转速fqs。针对式(17),暂时忽略虚拟转速项,其可以表达为:
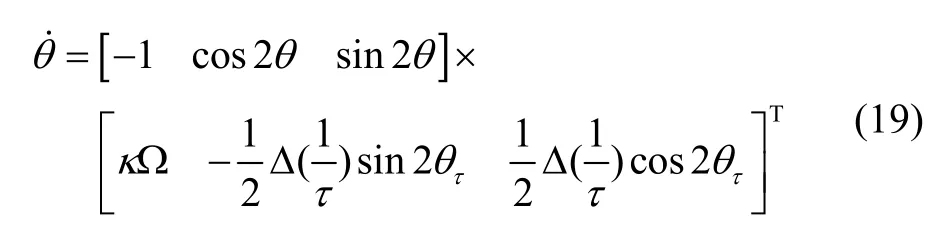
引入观察向量A和参数向量B,满足式(20):

陀螺阻尼误差自适应算法就是不断采集陀螺驻波输出角度和角速率,采用递归最小二乘法不断调整参数向量B,利用现有参数向量B计算出陀螺角度输出,并使该输出不断接近采集得到的角度输出,最终参数向量B中的参数逐渐收敛于其真值。自适应阻尼误差补偿方案如图8 所示。

图8 全角陀螺自适应阻尼误差补偿方案Fig.8 Adaptive damping error compensation for WA gyro
4 阻尼误差自适应补偿验证
首先在Simulink 中对全角陀螺阻尼误差自适应补偿算法进行仿真验证,设置外界角速率输入为50 °/s,角度增益κ=0.8,阻尼误差 Δ(1/τ)/2=15°/s,阻尼主轴方位角θτ为60 °,采样时间ts为1 ms。陀螺阻尼误差参数辨识仿真结果如图9 所示。
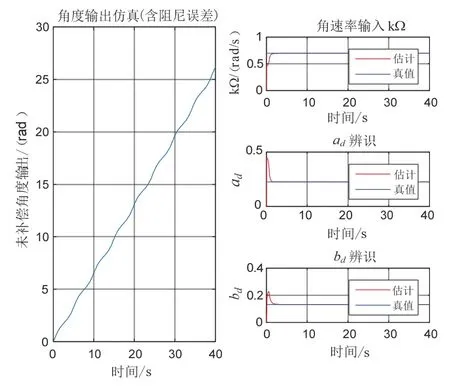
图9 全角陀螺阻尼误差参数自适应仿真结果Fig.9 Simulation results of adaptive damping error compensation for WA gyro
仿真结果表明,该陀螺阻尼自适应补偿算法能够在2 s 内完成对外界角速率输入、阻尼误差参数ad及bd的辨识。得到相关参数后,利用式(18)产生补偿虚拟旋转,抵消阻尼误差引起的角度输出误差。如图10所示仿真结果表明,利用阻尼自适应补偿能够有效降低阻尼误差导致的角度输出误差,其角度输出误差从未补偿的11.2 °降低至补偿后的0.009 °。

图10 阻尼误差补偿前后全角陀螺角度误差Fig.10 Simulation results of WA gyro angle error before and after damping error compensation
利用MEMS 多环陀螺搭建全角陀螺原理样机,如图11 所示,谐振子由40 个同心圆环组成,这些同心圆环通过分布的辐条相互连接,并最终连接到中心固体圆盘,谐振子的直径为2 mm。采用圆片级真空封装后,陀螺的品质因数约为40000。该MEMS 多环陀螺采用2θ工作模态,具有8800 Hz 的标称谐振频率。该多环陀螺具有16 个平行板电容电极,电极的间距为3 μm。进行模态间增益误差及刚度误差的抑制后,增益误差小于0.2%,频差小于0.1 Hz。由于角度误差与角速率输入成反比,在此测试更能反映阻尼误差的速率漂移值。

图11 MEMS 多环全角陀螺原理样机及测试设备Fig.11 Principle prototype and test equipment of MEMS multi-ring WA Gyro
此时陀螺驻波漂移主要受到阻尼误差的影响,利用阻尼自适应补偿法对陀螺阻尼误差进行补偿,陀螺驻波的角速率漂移如图12 所示,可见速率漂移从阻尼误差补偿前的2 °/s 降低为补偿后的0.25 °/s,性能提高了8 倍。

图12 全角陀螺阻尼误差补偿前后的速率漂移Fig.12 Test results of WA gyro rate drift before and after damping error compensation
5 结论
本文针对全角陀螺的阻尼误差,提出在阻尼主轴坐标系中采用能量衰减法对阻尼误差的影响进行研究,确定了全角陀螺的速率死区指标,进而在不同外界角速率输入情况下研究了阻尼误差对陀螺驻波进动的影响。针对阻尼误差的补偿提出了阻尼自适应补偿法,通过Simulink 理论仿真,结果表明陀螺角度输出误差从未补偿的11.2 °降低至补偿后的0.009 °;采用MEMS 多环陀螺进行实验测试,结果表明驻波速率漂移从阻尼误差补偿前的2 °/s 降低为补偿后的0.25 °/s,性能提高了8 倍,证明了阻尼误差补偿方案的有效性。

