开启生活之旅 品味数学之美

杨峰

在第6章，我们进一步学习了线段、射线、直线、角的有关性质以及直线的平行、垂直关系。我们在欣赏线段、射线、直线、角构成的许多美妙图形的同时，又学习到了从实践中得出的一些基本事实。这样，我们在看待一些生活中的问题时，学会了用数学的眼光去观察现实世界，用数学的思维去思考现实世界，用数学的语言去表达现实世界。

下面，让我们一起来开启一段数学之旅吧。

第1站，我们来到了一条河流旁边：

如图1，A、B是河l兩侧的两个村庄。现要在河l上修建一个抽水站C，使它到A、B两村庄的距离的和最小，请在图中画出点C的位置，并说明理由。

看到这个问题，我们立刻联想到了数学中的基本事实：两点之间线段最短。于是，这个问题我们就可以轻松解决：连接A、B，交直线l于点C，点C即为所求（如图2）。

第2站的问题接踵而来：

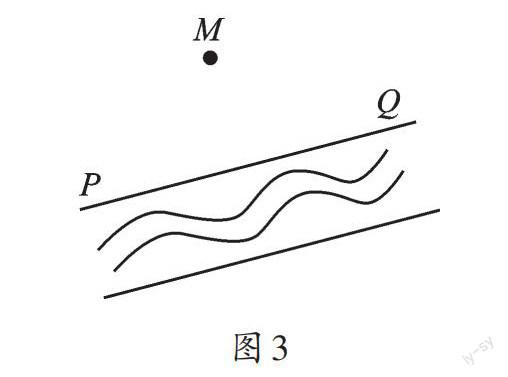
如图3，村庄M也准备在河PQ上修建一个抽水站，然后铺设输水管道，问应如何铺设管道，才能用料最省？试画出铺设管道的路线，并说明理由。

看到这个问题，你是不是又联想到了：直线外一点与直线上各点连接的所有线段中，垂线段最短。于是，这个问题可以这样解决：可过点M作MN⊥PQ，垂足为N，如图4，沿MN铺设管道，并把抽水站确定在点N处，就能用料最省。

数学之旅的第3站：

这次要请你在墙外测量两堵围墙构成的∠AOB的度数，如图5。

聪明的你，是不是联想到了对顶角相等？我们分别延长AO、BO，得到∠COD，然后通过测量∠COD的度数，可以得到∠AOB的度数。

看来，掌握一些数学的基本原理，对于解决生活中的实际问题是非常有效的。

第4站，我们放松一下，把眼光聚焦在一个台球桌上：

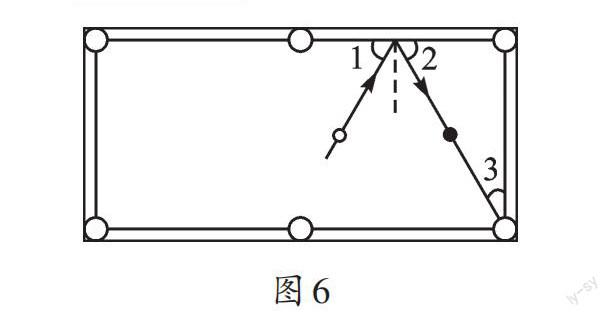
如图6，在长方形台球桌上打台球时，白球被击打后的行程路线与球桌的夹角∠1等于其反弹后的路线与球桌的夹角∠2。如果∠3=30°，为了使白球反弹后能将黑球直接撞入袋中，那么击打白球时，必须保证∠1的度数为_______________。

我们把这个问题转化到数学中来解决。根据直角三角形两锐角互余，可以求出∠2=90°-∠3=90°-30°=60°，然后就可以得出∠1=∠2=60°。看来，对角度多一点 “角感”，还能有助于我们打好桌球。

是不是信心满满？接下来我们到达数学之旅的第5站，这次遇到的问题比较棘手：

某公司员工分别住在A、B、C三个住宅区，A区有30人，B区有15人，C区有10人。三个区在一条直线上，位置如图7所示。公司打算在A、C之间只设一个班车停靠点，要使所有员工步行到停靠点的路程总和最小，那么停靠点的位置应在（ ）。

A.A区 B.B区 C.C区 D.不确定

这个问题怎么解决？因为A区的人数最多，B区的人数其次，C区的人数最少，所以班车停靠点就考虑设在A区与B区之间。我们不妨设停靠点距离A区xm处，那么可以算出员工步行到停靠点的路程之和=30x+15（100-x）+10（200+100-x）=4500+5x，由于x≥0，所以x=0时，路程和最小，那么停靠点的位置应该在A区。

看来，我们可以把现实中的线段问题结合代数运算进行有效解决。

同学们，生活中处处有数学，当我们遇到一些生活化的实际问题时，不妨把这些问题转化成数学问题，再结合我们所掌握的数学知识去尝试解决问题，往往能收获意外的惊喜。

（作者单位：江苏省无锡市东林中学）