样本估计总体在生活中的应用例析

山东省阳信县幸福中学 菅会娟

有时由于研究对象个体太多，限于人力与物力而无法做全面的调查，抑或调查时具有破坏性，我们只能抽样调查.抽样的方法包括简单随机抽样、分层抽样，以及整群抽样和系统抽样等.从总体中抽取一部分个体，得到样本，如何用样本估计总体呢？有两种途径：一是从图形的角度用样本估计总体，它需要用频率分布表列出各小组的频数与频率，抑或用频率分布直方图画出频数；二是从代数的角度用样本估计总体，即算出样本的平均数、方差和极差等，用样本的特征数估计总体的特征数.本文中运用实例说明如何在实际生活中用样本估计总体，以及具体的方法步骤和注意事项.

1 用捕捞的鱼估计鱼塘里的鱼

鱼塘里养了一定数量的鱼，如何知道这些鱼的总质量呢？我们不可能将鱼全部打捞上来称其质量，只能用样本估计总体，即捕捞部分鱼称其质量，求出鱼的平均质量，把样本中鱼的平均质量作为总体中鱼的平均质量，再乘鱼的条数，进而估计鱼的总质量.

例1久盛养殖专业户养了2 000条大肥鱼，现到了捕捞销售的时机，户主想知道这些鱼的总重量，现进行了三次取样，且记录列表如下：

鱼的条数每条鱼的平均质量/kg第一次捕捞151.6第二次捕捞152.0第三次捕捞101.8

(1)利用以上数据估计每条鱼的质量.再估计所有鱼的总重量，如果户主探知今天的鱼7.5元/kg，那么户主可收入多少钱？

(2)户主鱼塘的鱼有大型鱼与小型鱼之分，且大型鱼与小型鱼的价格不相同，分别为10元/kg和6元/kg，如果此时收入仍不低于第(1)问中的收入，那么鱼塘中大型鱼的总质量最少不能低于多少？

解析：(1)根据平均数的公式求解，每条鱼的平均质量×总条数=总质量，总收入=总质量×7.5.

每条鱼的平均质量=(15×1.6+15×2.0+10×1.8)÷40=1.8(kg)；总质量=1.8×2 000=3 600(kg)；总收入=3 600×7.5=27 000(元).

(2)列不等式求解.设户主大型鱼的最小质量为xkg，根据“此时收入仍不低于(1)中的收入”，得10x+6(3 600-x)≥27 000，解得x≥1 350.

答：鱼塘中大型鱼的总质量最少不能低于1 350 kg.

评注：本题中样本的平均数为加权平均数，因为表格中三个平均数的对应鱼的条数不同，即权重不同，所以不能用三个数的平均数作为三次捕捞的平均数.在不等式的应用里，一般设一个未知数建立不等式求解，尽量不设两个未知数，因为二元不等式的解法比较复杂，且超出学生目前所学范围.

2 用抽到的青年估计未被抽到的青年

微信是目前使用较广的一种信息交换工具，为了解人们使用微信的时长及年龄段情况，且由于这样的调查不具有重大意义，所以使用抽样调查即可，即用样本的特征数来估计总体的特征数.在调查中发现，使用微信的人群以青年人和中年人居多，且他们每天使用微信的时长大多数在一小时以上，说明微信已成现代人类生活的必备工具.

(1)根据以上信息，完成下表：

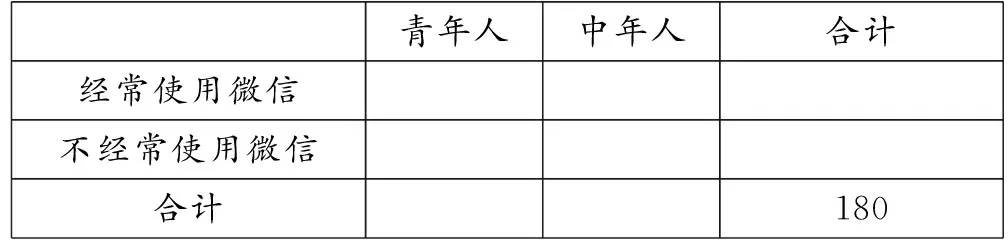
青年人中年人合计经常使用微信 不经常使用微信 合计 180

(2)拥有4 000万人口的某个省份，估计一下每天使用微信超过1小时的青年人(即年龄不过40岁)有多少？

解析：(1)根据题意逐条分析求解.

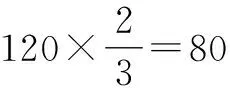
青年人中不经常使用微信的人数为135-80=55，因为经常使用微信的人数为90+30=120，所以不经常使用微信的人数为180-120=60.故中年人中不经常使用微信的人数为60-55=5，补全表格如下：

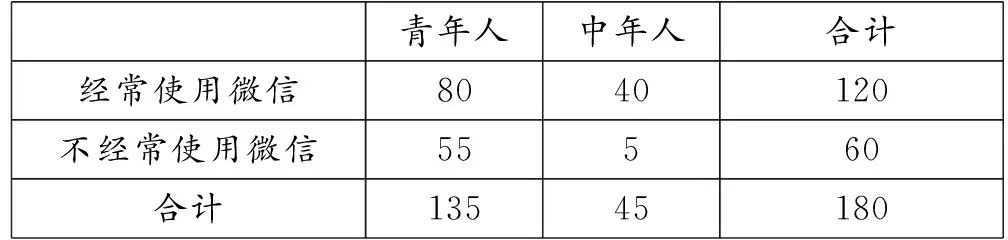
青年人中年人合计经常使用微信8040120不经常使用微信55560合计13545180

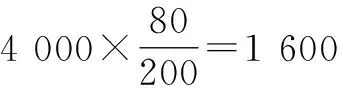
评注：本题涉及的量比较多，共有6个相关的量，解答时要先从易求的量入手，随着求出量的增多，解答会越来越容易.本题运用成比例增长的方法，用样本估计总体，即将样本中的百分率作为总体中的百分率进行估计.

3 用一周的用电量估计一月的用电量

现代家庭随着家用电器的增多，用电问题成为大家越来越关注的话题.如何在月初预测出这个月将会使用的电量呢？需要使用样本估计总体，可以通过连续几天的观察，得到几天的用电量，求出样本的平均用电量，用这个平均用电量乘本月的天数可估计出全月的用电量.

例3张经来家喜迁新居，又增加了一些新的电器，在这种状况下，一个月用多少度电呢？他在六月份的第一个周观察了电表示数，记录如下：

日期电表显示度数/(kw·h)1日1152日1183日1224日1275日1336日1367日1408日143

(1)张经来家六月份将用多少度电？

(2)张经来使用一周的用电量来估算整个一年的用电情况合适吗？

(3)如何估算张经来家整个一年的用电量更合适？

解析：(1)先求一周的总电量，除天数得每天的平均用电量，再乘以30天，得一个月的用电量.7天的总用电量=143-115=28(kw·h)，每天的平均用电量=28÷7=4(kw·h)，六月有30天，故这个家庭六月份的总用电量为4×30=120(kw·h).

(2)根据电器的季节使用情况判定.因为六月份属于夏季，用电量较大，所以用这个月的用电量估计全年的用电量不妥当.

(3)每种电器的使用情况不一样，要分别估计用电量，再估计一年的用电情况.

评注：电度表每天都有一个示数，每天的用电量应该用第二天的示数减去第一天的示数，一周的用电量应该用周一的示数减去上周一的示数.本题不仅考查了用样本估计总体，而且还考查了抽样调查的合理性，抽取的样本具有代表性和广泛性，才是合理的.

4 用树苗成活率估计成活的树苗

由于受土壤、气温、人工操作等诸多因素的影响，移栽树苗时一般不可能100%成活，都有一定的成活率，这是我们都必须承认的事实，所以园林公司要想得到成活后的一万棵树苗，那么开始移栽的树苗数量必须大于一万棵，到底多移栽多少棵呢？我们可以通过实验的方法找到成活率，用一万棵除以成活率就可以得到开始移栽的数量.

例4南方某市市政公司培育出新品种风景树苗，为考察这种风景树苗的移植成活率，调查人员进行了统计，结果如下表所示.

累积移植总数/棵1005001 0002 0005 00010 000成活率0.9100.9680.9420.9560.9470.950

这个城市实施打造人类宜居环境，需移植一批这种树苗，若这批树苗移植后要有28.5万棵成活，那么需要一次性移植多少棵树苗，较为合适？为什么？

解析：由题中表格可知，随着树苗移植数量的增加，树苗移植成活率越来越稳定.当移植总数为10 000时，成活率为0.950，于是可以估计树苗移植成活率为0.950，则该市需要购买的树苗数量约为28.5÷0.950=30(万棵).

评注：此题是用多次重复试验得到成活率，则可将频率的稳定值作为一棵树苗成活的概率，然后用成活的树苗数除以频率，得到总数，即移植树苗的数量.整个解答过程可分为两步，一是先用频率估计概率，二是再用样本概率估计总体概率.

用样本估计总体的应用还包括在摸球试验中，用摸出一种颜色球的频率，估计口袋里小球的总数量等，但是无论我们如何抽取样本，样本总是总体的一部分，样本的平均数只能反映样本的集中趋势，然而总体的集中趋势只能由总体平均数反映最准确，两个量不可能完全相同，有一定的差异，只能尽可能接近，我们得到的是一个估计值.