分级循环加卸载下砂岩损伤力学特性研究
蔡国军,孙文鹏,陈锡锐,杨森林,贾 俊,李 林
(1.成都理工大学 地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059; 2.成都理工大学 地质工程国家级实验教学示范中心,四川 成都 610059; 3.中国地质调查局西安地质调查中心/西北地质科技创新中心自然资源部黄土地质灾害重点实验室,陕西 西安 710054)
0 引 言
矿井开采,隧道开挖等实际工程中经常发生岩石的反复加卸载过程。而我国又是一个地震多发的国家,震害导致岩体开裂并引发其他次生灾害[1]。循环加卸载下岩石的力学特性及能量演化特征与常规受力条件时不同[2]。所以对于岩石循环加卸载过程中损伤力学特性的研究十分必要。
针对动态单轴下岩石力学特性的研究目前已有很多,邓华锋在砂岩单轴循环加卸载试验中提出,应将残余应变与应力-应变滞后现象纳入对影响能量参数的考虑范围[3];周家文对脆性砂岩进行了单轴循环加卸载试验与声发射试验,并基于此研究了一种循环荷载下简化计算弹性常数的方法[4];杨春和通过对盐岩变形特性的研究发现单轴循环荷载下的变形参数相比于静态单轴压缩试验更能揭示盐岩地下工程中的变形特性[5]。E.Eberhardt在脆性岩石单轴循环加卸载试验中,对岩石破坏过程中的损伤力学特性进行了研究并对微裂纹扩展的影响因素与破裂准则进行了分析[6-7]。李宏岩对低温下砂岩进行了冲击压缩试验,研究发现低温下砂岩的破坏是岩样内部微裂纹在温度与冲击荷载共同作用的结果[8]。
大多实际工程岩体都处于三向应力状态,受到轴向与径向的约束,处于有围压的环境中。单轴试验忽略了围压的影响,不能完全体现围岩体的实际受力状态,脱离了围岩地质环境。近年来,涌现了大批的学者研究高围压下岩石三轴循环加卸载的损伤力学特征与破坏过程[9-10]。苗胜军,刘泽京等在花岗岩的三轴循环加卸载试验中探究了花岗岩的能量演化特征,基于能量角度定义了新的岩石损伤变量[11]。孟庆彬,王从凯等为了探究围压对灰岩能量演化特征的影响规律,设计了不同应力路径下的循环加卸载试验并对此进行了研究与分析[12]。李子运,吴光等建立了基于能量突变的页岩强度失效判据,揭示了受压过程中页岩的能量演化特征与规律[13]。荣笛等在饱和板岩的三轴循环加卸载试验中对板岩的滞后特性与围压的关系进行了探究,发现岩样的滞后特性是由围压增加所导致[14]。赵星光等在花岗岩的循环加卸载试验中,进行了花岗岩的力学特性和变形特征相关方面研究[15-18]。然而对于低围压下岩石三轴循环加卸载的变形破坏与损伤力学特性相关方面的研究还不是很成熟,故对陕西省略阳市某滑坡表层的中风化砂岩取样,通过成都理工大学国家重点实验室的MTS815电液伺服岩石力学试验机对砂岩进行静态单轴压缩试验和三轴循环加卸载试验。研究低围压循环加卸载下砂岩的力学参数分析,强度变形特性以及损伤特征,为工程岩体的损伤力学特性研究提供理论指导。
1 砂岩循环加卸载试验条件及方案
按国际岩石力学学会建议方法[19]将砂岩样制成Φ50 mm×100 mm的标准岩样,两端并用金刚砂打磨,控制端面平整度在±0.05 mm内,以此避免加载时产生局部应力集中现象。对岩样进行声波波速测定,筛除波速异常那一部分,维持试样的均一性。
加载仪器采用MTS815Teststar程控伺服岩石力学试验机见图1,振动波形为正弦波,频率1 Hz。一组共六个岩样,取其中两个试样进行常规单轴压缩全过程试验,以确定试样的单轴抗压强度和泊松比。剩下四个试样分别进行围压为0 MPa、1 MPa、2 MPa、3 MPa的循环加卸载试验。本次试验为荷载下限保持不变,上限等级升高的三轴循环加卸载试验,每次试验共有七级荷载。从单轴抗压强度的20%开始,荷载上限增加幅值均占单轴抗压强度的10%,逐级递增到单轴抗压强度的80%,每级荷载以1 Hz的频率循环30次,若试样中途破坏则立即停止试验,若没有破坏则加载至最后一次循环后停止试验。试验加载方案见图2。

图1 MTS-815型程控伺服刚性试验机

图2 试验加载方案
2 砂岩循环加卸载试验及静态单轴压缩试验结果与强度变形特征
2.1 静态单轴压缩试验
取砂岩试样置于无侧限单轴压缩条件下,进行静态单轴压缩试验用以测定该试样所能承受的最大压应力-单轴抗压强度[20]。并在此基础上,通过测定的应力-应变曲线计算求得所能表征该试样的基本物理力学参数,即泊松比与弹性模量,为后续循环加卸载试验的参数设定提供参考。
早期施加荷载时,试样内部原有的裂隙逐渐被压密,轴向应变增加显著,而横向应变保持在很小的变化范围内。如图3、4所示,弹性变形阶段后,“转化为似连续介质”的砂岩可以被近似看作弹性体,轴向应变呈线性增加,横向应变变化范围此时依旧很小。裂隙稳定发展阶段后,便进入塑性变形阶段,曲线主要呈非线性增长,14 MPa左右时,轴向应力骤然下降后又快速上升。这是由于加载过程中,试样局部产生贯通裂隙,轴向应力快速下降,但就试样整体而言,局部裂隙并没有达到贯通,未破坏区域会阻碍局部裂隙继续发育,试样整体还是呈稳定状态,加载仍在进行,故轴向应力依旧会上升,但在宏观上表现为横向应变和体积应变的急剧增大。随着加载的进行,局部裂隙的数量增多,试样整体产生贯通裂隙,最终发生破坏。在峰后应力应变曲线中,可观察到明显的残余阶段,应力跌落后保持小范围的波动,破坏后的试样仍具有抵抗部分荷载的能力,当砂岩试样进一步破坏时,发育裂隙面间摩擦力增大,裂隙由于下跌后的应力过低很难继续完全发育贯通,故需应力进一步增大使得砂岩试样完全破坏。图4,峰后应力应变曲线迅速下降,并没有出现明显的残余应变,这是由于试样破坏时,内部发展的裂隙比较贯通,裂隙面间的摩擦较小,属于典型的脆性破坏。
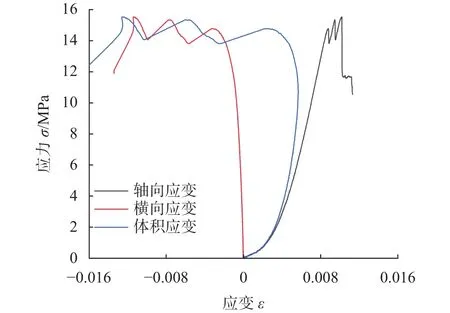
图3 试样1-1单轴应力-应变曲线

图4 试样1-2单轴应力-应变曲线
2.2 三轴循环加卸载试验
当试样进行三轴循环加卸载试验时,每施加一级动应力,都伴随着有动应变的产生。这是由岩样微观结构的缺陷(解理,裂隙等)所造成的。所以对岩样施加荷载时,不仅会产生弹性应变,也会产生塑性应变即不可逆应变。由于动应力-动应变的滞后效应,导致一些时间差,从而产生塑性滞回环曲线。加压时会使岩样中的原始缺陷裂隙闭合,而后卸荷时,原本紧贴在一起的裂隙逐渐变松,加卸载曲线呈内凹状,随着试验的进行,在轴向荷载的作用下,滞回环曲线总会向应变增大的方向转移且转移过程是不可逆的。由于本文篇幅有限,故取每级循环中第25次振动周期为研究对象。如图所示,初期轴向荷载较小时,岩样内部微观裂隙被逐渐压密,此时轴向荷载较低不利于岩样内部结构裂隙的发育,当轴向荷载增大到一定程度时,岩样内部裂隙逐渐发育,抵抗变形能力逐渐降低,轴向应变变化范围较大且快,发生剪胀,转化为剪胀状态时对应的荷载值称之为“临界荷载值”。如图5~图8所示,图5中滞回环曲线内凹现象越来越明显,说明岩样产生不可逆应变能力逐渐变强,由于施加动荷载的原因,每级荷载都会使曲线向前移动,产生推进现象。由围压0 ~3 MPa变化过程中,滞回环曲线逐渐平直,内凹现象越来越“模糊”,3 MPa时尤为明显,说明围压会限制岩样产生不可逆应变,但总体趋势仍是向前推进,塑性变形能力逐渐变强。
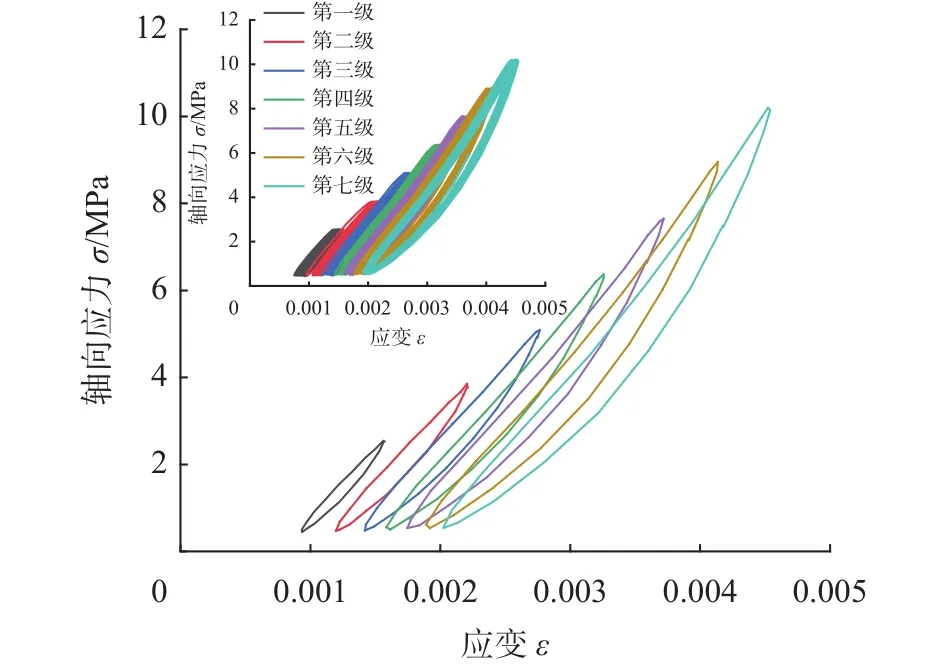
图5 围压0 MPa第25次滞回环
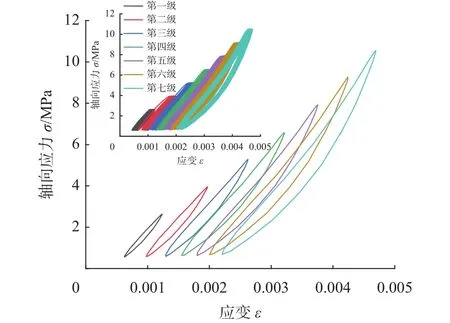
图6 围压1 MPa第25次滞回环
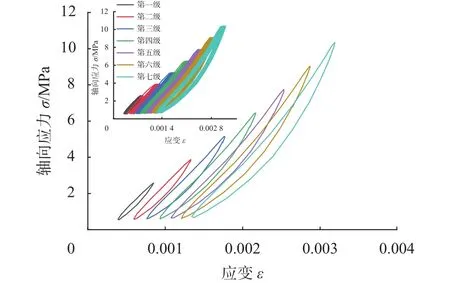
图7 围压2 MPa第25次滞回环

图8 围压3 MPa第25次滞回环
3 砂岩循环加卸载试验力学参数分析
3.1 应变参数分析
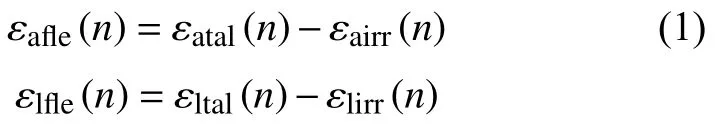
式中: εafle(n)、εlfle(n)——第n次循环时轴向axi与环向lat的弹性应变;
εatal(n)、εltal(n)——第n次循环时加载到峰值点所对应的轴向axi与环向lat总应变;
εairr(n)、εlirr(n)——第n次循环时卸载后的轴向axi与环向lat塑性应变即不可逆应变。

式中: Δεairr(n)——第n次 循环时轴向axi绝对不可逆应变;
εairr(n)、εairr(n-1)——第n次及前一次循环时卸载后的轴向axi不可逆应变。
为了探究不同围压条件下,砂岩循环加卸载试验过程中轴向总应变、不可逆应变的变化规律,取20、40、60、80、100、120、140、160、180、200 循环周次滞回环为研究对象,绘制轴向总应变及不可逆应变与循环次数的关系曲线图。如图9、10所示,随着循环周次的增加,总应变与不可逆应变曲线均呈近似线性增加。相同轴向荷载下,三轴循环加卸载时产生的总应变、不可逆应变均低于单轴循环加卸载(由于试样的差异性,围压1 MPa时试验后期岩样临近峰值强度,故应变增长较快,超过了单轴时的应变),三向应力状态下,围压的作用使岩样内部原始裂隙闭合并限制其变形发展。观察三轴循环加卸载曲线也可以看出,随着围压的增大,相同循环次数下轴向总应变与不可逆应变逐渐降低,但相同围压时轴向总应变与不可逆应变总体趋势均是增大。循环加卸载试验过程中,岩样原始裂隙不断被压密与扩张,当荷载达到“临界荷载”时,岩样开始产生新的裂隙并不断扩展,逐渐累积不可逆应变如图10所示。
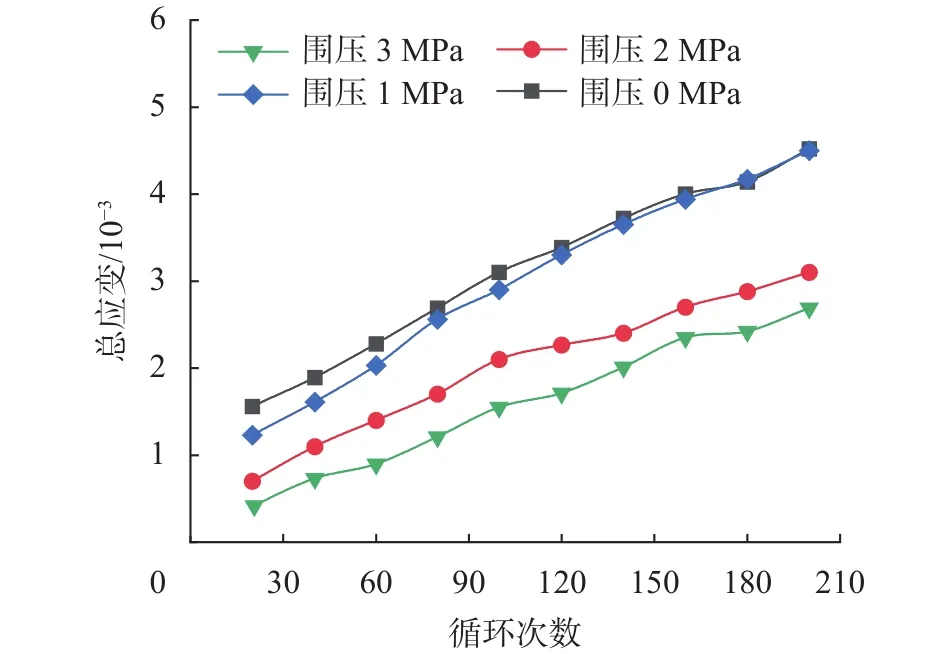
图9 总应变与循环次数关系曲线
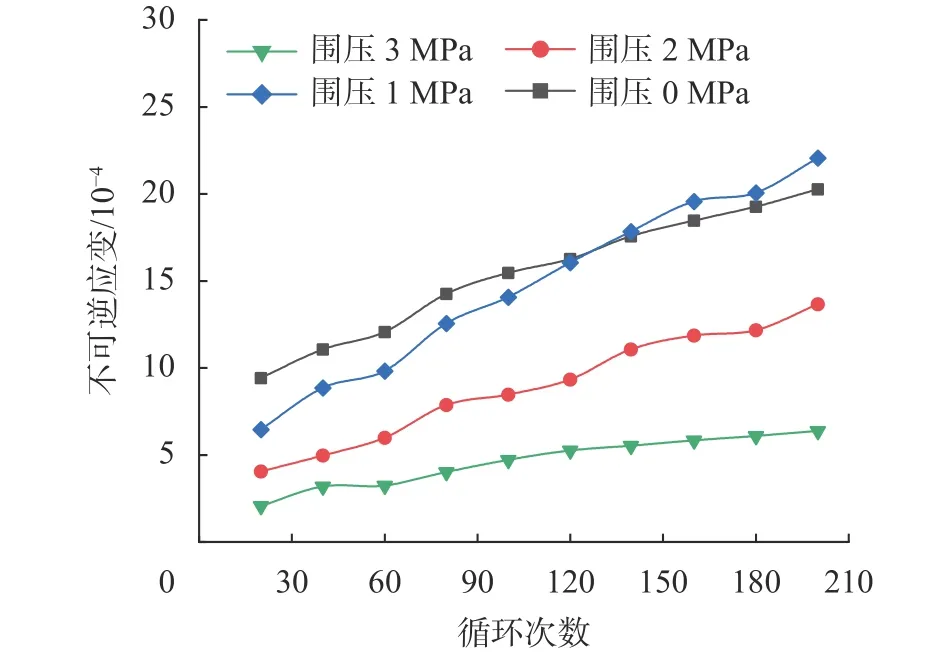
图10 不可逆应变与循环次数关系曲线
为了更直观的表征循环加卸载时不可逆应变随试验进行的变化规律,绘制绝对不可逆应变与循环次数关系曲线图。如图11所示,试验早期由于应力上限水平较低,处于压密阶段,岩样内原始缺陷裂隙被不断压密,此阶段大部分被压密的裂隙并不会在卸载时恢复,故曲线趋势不断上升。随着应力上限水平的增大,初始裂隙不断经历闭合与扩张,循环阶段变形逐渐稳定,曲线趋势略微下降并保持小范围波动。弹性变形与裂纹稳定发展阶段时,此阶段应变主要受弹性变形控制,卸载时大部分应变逐渐恢复,曲线趋势略微下降,但总体保持稳定波动。后进入裂纹不稳定破裂发展阶段,绝对不可逆应变增加趋势明显增大,裂隙逐渐贯通。
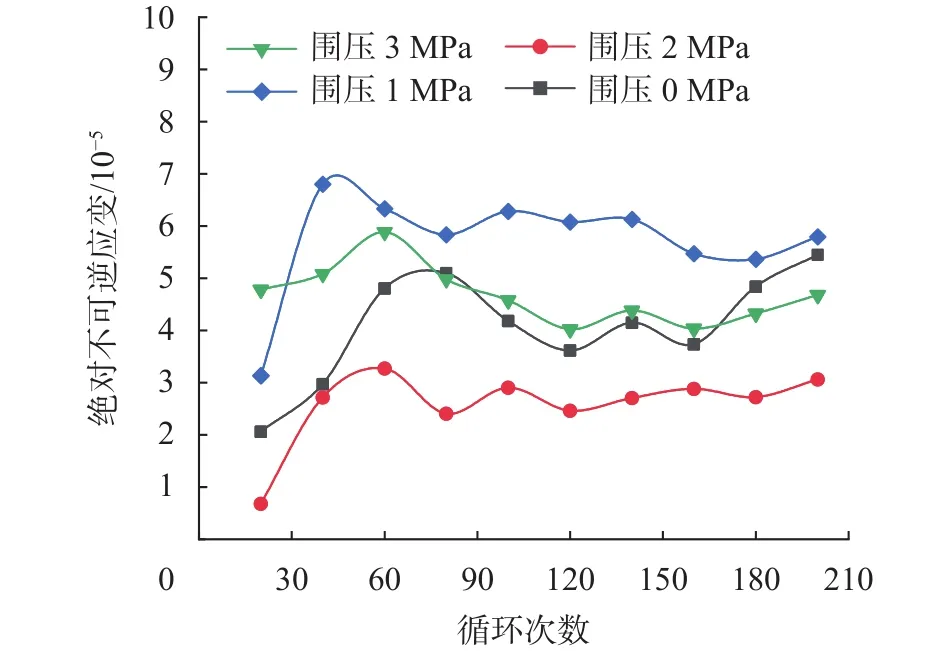
图11 绝对不可逆应变与循环次数关系曲线
3.2 动弹性模量与动泊松比分析
循环加卸载试验中动弹性模量Ed与动泊松比µd的计算公式分别为:
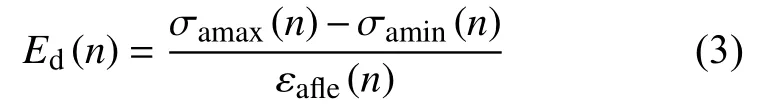
式中:Ed(n)——第n次循-环时动弹性模量;
σamax(n)、σamin(n)第n次循环时轴向axi最大、最小动应力;
εafle(n)——第n次循环时轴向axi的弹性应变。

式中: µd(n)——第n次循环时动泊松比;
εafle(n)、εlfle(n)——第n次循环时轴向axi与环向lat的弹性应变。
动弹性模量随循环次数变化呈开口向下的抛物线,如图12所示。对比不同围压条件动弹性模量可得,相同循环周次(轴向应力)水平三轴循环加卸载下动弹性模量明显大于单轴循环加卸载条件下,围压的施加会限制其发生应变,增强岩样抵抗变形的能力,刚度增大从而弹性模量提高。围压为1,2,3 MPa时曲线也可看出,随着围压的增大,同一轴向应力水平下动弹性模量逐渐变大。试验加卸载初期,岩样内部原始裂隙在较小的循环上限应力水平作用下不断闭合,此部分闭合的裂隙在卸载时并不能完全张开,岩样内部裂隙重新调整,结构硬化,增强了砂岩试样的力学性质,总体处于压密阶段,曲线趋势不断上升。弹性变形阶段及裂纹稳定发展阶段时,岩样内部原始裂隙调节完毕并逐渐发展新的裂隙,此阶段主要发生弹性应变,大部分变形卸载时都能恢复,动弹性模量保持稳定或小范围波动。随着应力上限水平不断增大临近峰值时,岩样抵抗变形能力逐渐降低,损伤累计加剧,裂隙不稳定扩展,动弹性模量逐渐降低。但由于应力上限加载到80%单轴抗压强度后停止试验,围压0,1 MPa时岩样临近180次循环后,动弹性模量逐渐下跌,而围压2,3 MPa时岩样动弹性模量还未来得及下跌,变化趋势不如其明显。
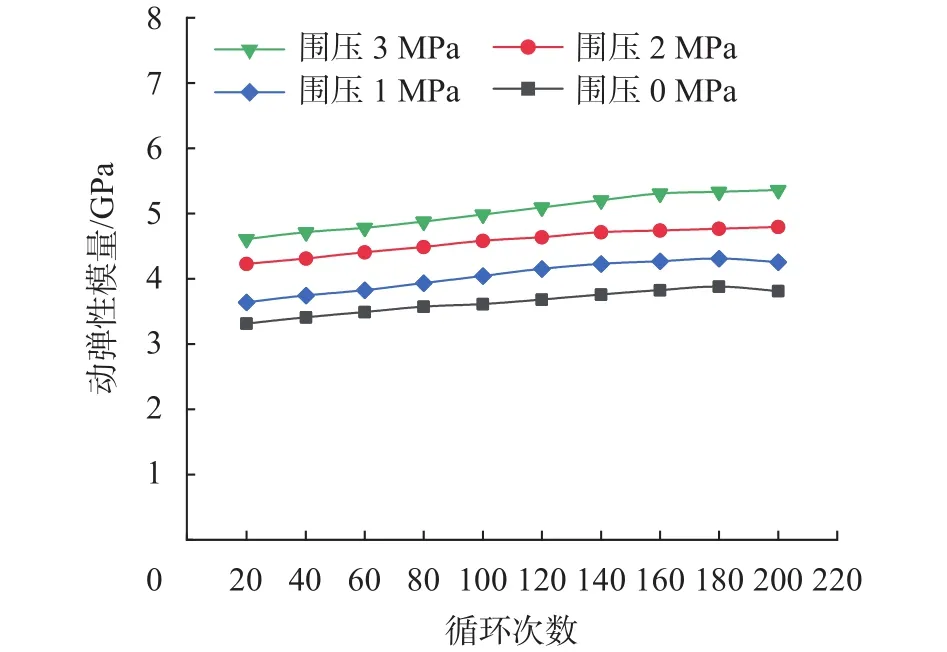
图12 动弹性模量与循环次数关系曲线
循环加卸载试验过程中,动泊松比随循环次数增加呈现出不断增大的趋势,如图13所示,试验后期砂岩试样抵抗变形能力逐渐降低,动泊松比增加幅度明显。单轴条件下砂岩试样的动泊松比明显高于同应力水平时三轴条件下的动泊松比,围压限制了砂岩试样的变形发展,且随着围压增高,动泊松比变化趋势逐渐减小。

图13 动泊松比与循环次数关系曲线
4 砂岩循环加卸载试验损伤力学特性研究
4.1 滞回环形状特性分析
由前述可知,试验加载时产生的总应变包括弹性应变和塑性应变,弹性应变在卸载时全部恢复,塑性应变得以保留。能量在岩样内部不断消耗故产生一定的损伤,积累起损伤所需的能量称之为耗散能。忽略掉残余变形以及滞后效应部分的能量,可以近似的将滞回环面积比作耗散能。通过图5~图8计算得到各循环级数滞回环面积,建立滞回环面积与循环级数相关曲线如图14所示。同一循环级数时,滞回环面积随着围压的增大而逐渐减小,即在高围压下岩样内部原始缺陷以及新鲜裂纹的扩展贯通程度都在降低,积累起损伤所需要的耗散能不断缩减,塑性应变即不可逆应变也在减少。反而相同围压时,滞回环面积随着试验进行不断增大,试样塑性变形不断累积,对应其应变及其变形所消耗的能量不断增加。但其增长速率表现不一,如前所述,试验早期岩样内部缺陷仍处于压密阶段,大部分变形在卸荷时并不会恢复,塑性变形变化较快,故曲线增长趋势较快。中期时,岩样产生以塑性变形过渡到以弹性应变为主的变化趋势,此时塑性变形仍在进行,故损伤仍在积累,滞回环面积仍在增大但增长趋势略有下降。当循环应力增大从而临近峰值强度时,岩样内部裂纹扩展加剧并逐渐贯通,滞回环面积明显增大,损伤逐渐积累。

图14 滞回环面积与循环级数关系曲线
4.2 损伤变化情况分析
循环加卸载试验过程中,岩样的损伤意味着原始缺陷裂纹的闭合与扩张,新生裂纹的发育并逐渐接触贯通的过程。根据岩石损伤的定义,计算循环加卸载损伤参数公式如下。
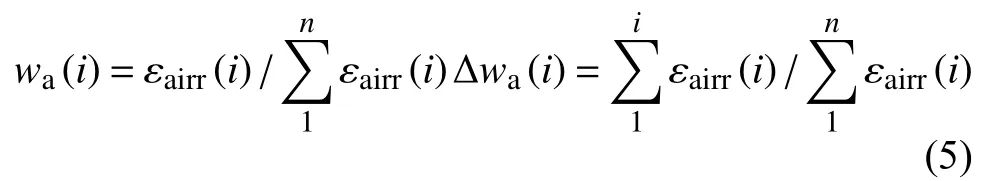
式中:wa(i)、Δwa(i)——第i次循环轴向应变的损伤参数、累计损伤参数;
εairr(i)——第i次循环轴向不可逆应变;
n——总循环加卸载次数。
不同围压下砂岩试样轴向损伤参数与循环次数关系曲线如图15、16所示,相同围压下轴向损伤参数均随着循环次数的增大呈现出增大的趋势,这也验证之前所述轴向不可逆应变随着加卸载的循环不断增大。加载初期轴向绝对损伤参数增长明显,由于初始循环荷载作用使得岩样原始缺陷裂纹不断被压密、压实,但此时并没有达到岩样的“临界荷载”故几乎没有新鲜裂纹的产生,所以岩样累计损伤较小。随着循环次数的增多,岩样绝对损伤参数增长趋势变慢,累计损伤参数仍不断积累,新鲜裂纹逐渐发育和扩张,加载后期砂岩损伤变量增长趋势陡增,损伤加剧。对砂岩试样进行循环加卸载试验时,随着围压的增大,砂岩试样抵抗变形破坏能力增强,损伤不断积累并逐渐增大。

图15 轴向绝对损伤与循环次数关系
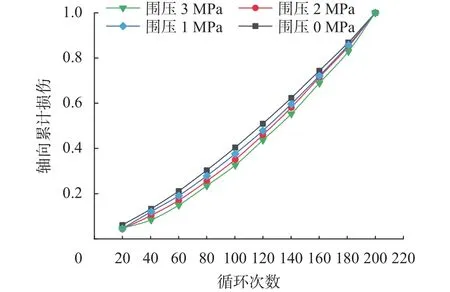
图16 轴向累计损伤与循环次数关系曲线
5 结束语
基于砂岩静态单轴压缩试验与三轴循环加卸载试验,研究了砂岩试验过程中的变形与损伤特性,得出了以下结论:
1)循环加卸载试验过程中,围压越大砂岩试样内凹现象越“模糊”,但总体趋势向前推进。
2)随着围压增大,砂岩抵抗变形破坏能力增强,动弹性模量明显增大,泊松比逐渐降低,但相同围压下,试验后期砂岩发生扩容逐渐处于应变软化状态,泊松比增幅明显。
3)滞回环面积受围压与轴向载荷影响明显,与围压变化呈负相关,与轴向载荷变化呈正相关,轴向载荷增大时,不可逆应变逐渐累积,砂岩损伤加剧。
4)就砂岩循环试验力学特性来说,早期循环荷载作用下岩样内部原始裂隙被压密、闭合,可观察到明显的弹性强度与变形特性增强现象,后过渡到以弹性变形为主的裂纹稳定扩展阶段,随着试验进行,裂纹逐渐加剧扩展并贯通,岩样逐渐失稳,损伤累计达到峰值。

