一种用于滑坡位移监测的OFDR测斜仪研发

张 峰，裴华富

(大连理工大学岩土工程研究所，辽宁 大连 116024)

0 引 言

滑坡是一种严重的全球性自然灾害，给人们的生命财产造成了巨大损失。边坡监测是滑坡灾害防治研究的重要组成部分[1-2]。根据地表位移、地下水压力、桩身位移、锚固应力、深部位移等监测对象的不同，大致可分为多种监测技术[3-5]。深部位移监测是其中必不可少的内容，可以获取边坡任意深度的水平位移，确定滑裂面和薄弱带的位置，有效判断边坡的稳定性。此外，该方法可用于监测所有滑坡和基坑坍塌变形。

测斜仪是监测边坡深部位移的主要设备。传统的测斜仪包括振弦式、伺服加速度计、应变式和电子式[6-7]。然而，这些传统的测斜仪存在稳定性差、电磁干扰大等缺点，并且大多属于点式监测，采集的数据量有限，难以满足边坡监测的要求。在过去的几十年里，分布式光纤传感（DFOS）技术得到了发展，包括光纤布拉格光栅（FBG）、光时域反射（OTDR）、布里渊光时域反射/分析（BOTDR/A）和布里渊光频域反射计/分析[8-11]。Ho[12]等应用时域反射（TDR）技术检测九峰山滑坡位移并测量其变形大小。该技术可有效监测滑坡滑动面的位置，边坡位移可以通过TDR反射波形的变化来确定。裴华富[3]等人研制了一种基于FBG的新型原位测斜仪。测斜仪的位移由光纤光栅传感器测得的应变经过有限差分法计算得到。Sun[8]等人开发了基于欧拉梁理论的BOTDR测斜仪，并将其安装在实际边坡上进行滑坡监测。然而这些技术在提高空间分辨率、监测精度、应变位移转换算法等方面仍存在一定的局限性。例如，TDR技术空间分辨率低，误差大。FBG属于准分布式技术，测点间距离较大，难以准确捕捉位移突变点处滑移面的位置。BOTDR技术虽然可以实现分布式测量，但其监测精度低于FBG技术。OFDR技术结合了分布式监测和高精度的优点，与传统的传感设备相比，具有明显的优势[13-14]，主要体现在以下几个方面：1)传感器的选择更简单，更广泛。温度和应变测量可以用普通的通信光纤进行，既便宜又简单；2)工作原理先进，空间分辨率可达1 mm，测量精度可达1 µε；3)使用的光缆为普通光缆，价格便宜，单根光纤可同时测量数千个传感点，测量精度高；4)分布式测量，传感器结构简单，测试性能稳定。

因此，本研究将OFDR技术应用于边坡监测。首先，研制了一种基于共轭梁算法的OFDR原位测斜仪。然后，通过数值模拟验证了共轭梁算法的有效性，通过对比实验验证了OFDR原位测斜仪的精度，通过模型实验验证了测斜仪的实用性。最后，对这些结果进行了讨论和分析，以验证基于共轭梁算法的OFDR原位测斜仪可以有效地用于边坡位移监测中。

1 监测方法

1.1 OFDR传感技术原理

当被测光纤置于温度场或应变场中时，光纤内部的折射率分布会在温度或应变的影响下发生变化，瑞利散射信号光的相应频率也会发生变化。通过测量瑞利散射信号光的频率可以得到对应外部温度场或应变场的变化，从而实现分布式光纤传感测量。

OFDR的基本原理如图1所示。来自光源的线性扫描连续光被耦合器分成两路，其中一路作为参考光。另一个用作检测光并发射到要测量的光纤中。当检测光在光纤中向前传播时，会连续产生瑞利散射信号。这些信号光和反射参考光通过耦合器发生拍频干涉，被光电检测器检测到。将参考光和检测光得到的瑞利散射信号分成若干个信号窗口，通过互相关运算计算每个信号窗口的光谱偏移量。谱位移与应变和温度变化的关系可用下式表示[13-14]：

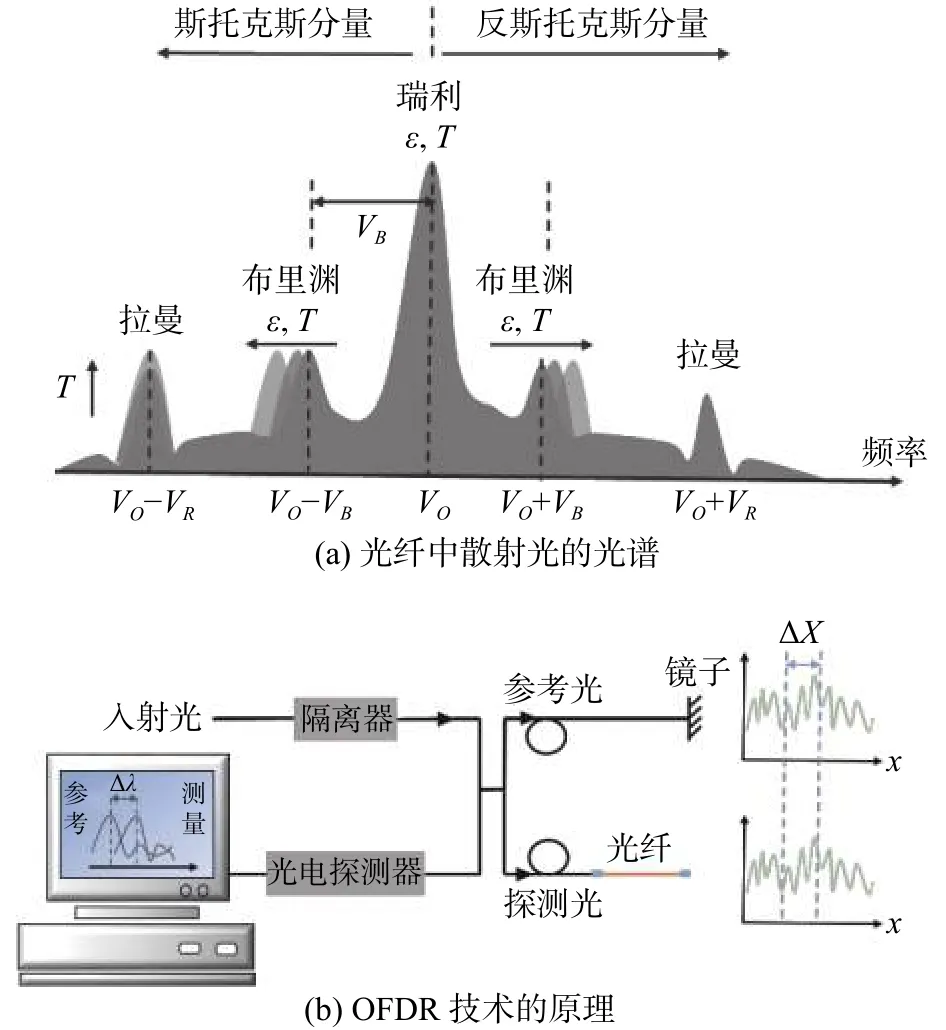
图1 OFDR技术示意图（改自文献[13]）

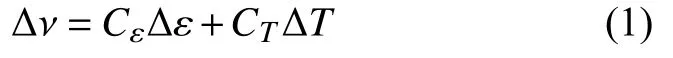
其中Cε和CT是校准常数。

1.2 OFDR测斜仪设计

基于上述OFDR技术，设计了测斜仪。将一根横截面直径为20 mm，长度为1 000 mm的PVC棒上刻出一个深度为2 mm的凹槽，将光纤预先拉直放入凹槽中，然后用环氧树脂胶进行粘贴制作测斜仪，如图2所示。

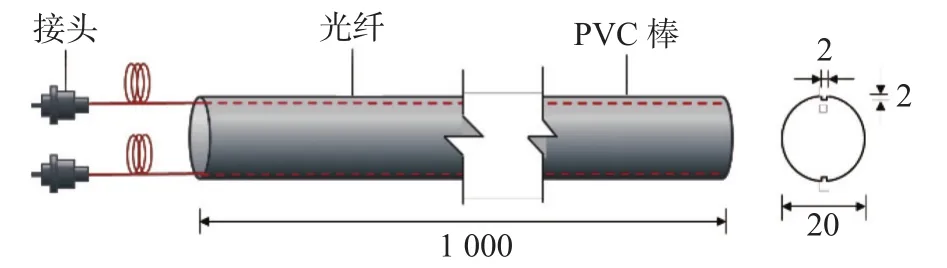
图2 OFDR原位测斜仪设计（单位：mm）

环氧树脂可以很好地将光纤和PVC棒粘合在一起，使光纤精确测量PVC棒表面的应变分布。OFDR技术可每1 mm取一个测点，获得一个应变值。对滑坡进行监测时，预先在边坡相应位置钻孔，将OFDR原位测斜仪垂直插入钻孔内，如图3(a)所示。当边坡在地震、降雨或外部荷载作用下产生滑动时，由于PVC棒具有良好的弹性，能随土体协调变形。根据PVC棒表面光纤测得的应变，结合相应算法可计算出OFDR原位测斜仪的位移，从而反映边坡的变形，判断边坡的稳定状态。

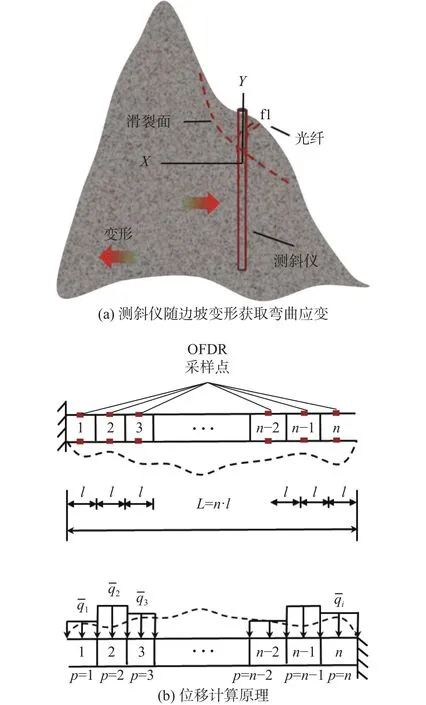
图3 位移计算示意图

1.3 位移计算方法

测斜仪垂直插入边坡中，可视为悬臂梁，下端固定，上端自由。假设测斜仪的水平位移相对于测斜仪的长度较小，即满足材料力学中的小变形假设，忽略剪切变形的影响，则测斜仪可视为小变形欧拉梁，满足曲率k与弯矩M的物理关系：

式中：E——材料的弹性模量；

I——截面的惯性矩。

在共轭梁理论中[5]，实梁的挠度和角度对应于共轭梁的弯矩和剪力。实梁的曲率在数值上等于共轭梁的荷载集度。基于该理论，可以实现悬臂梁的挠度计算。结合材料力学，可以建立如下关系：

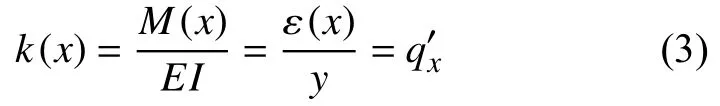
式中： ε(x)——光纤测得的测斜仪各点的应变；

y——弹性梁的半径；

假设测斜仪的长度为L，按照OFDR技术的采样间隔，L被分为n个单元，则每个分段的长度为l=L/n。各单元上下表面分别取两个应变监测点，简化模型如图3(b)所示。各截面载荷分布可表示为：

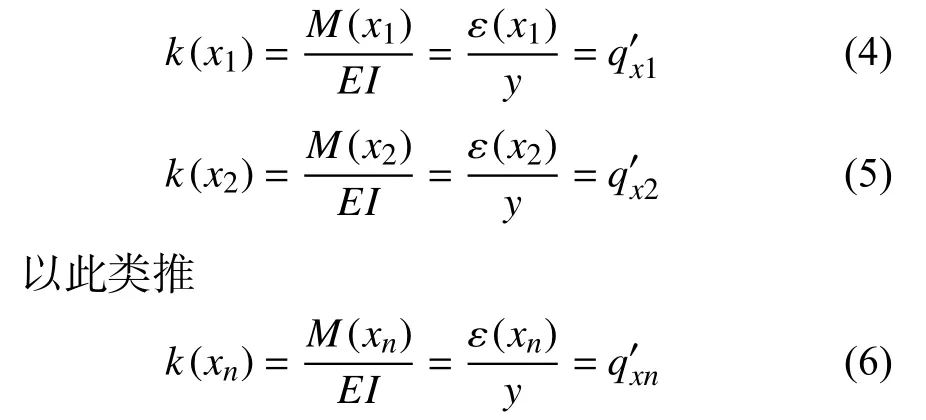
根据共轭梁的荷载分布，可以计算出共轭梁上任意一点的弯矩。

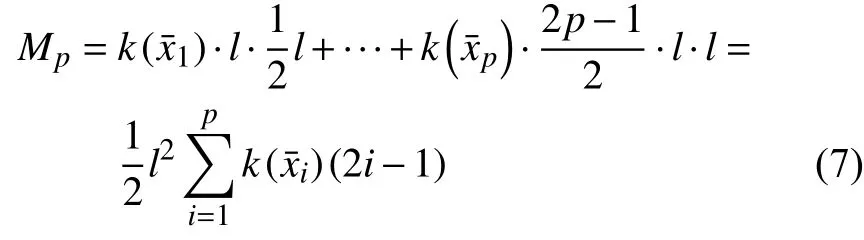
根据实梁与共轭梁的关系，可以得到实梁上任意一点的挠度。为方便计算，将式（7）转换为如下矩阵：

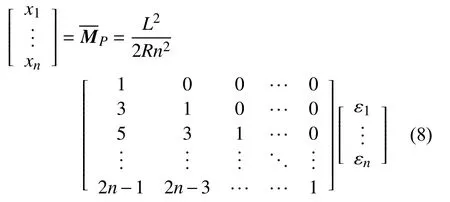
2 共轭梁算法的有限元验证

采用有限元数值模拟方法验证共轭梁法用于测斜仪中计算位移的准确性。在Abaqus中建立长度为2 m，半径分别为2 cm、3 cm和4 cm的悬臂梁模型。梁的弹性模量和泊松比分别为3 000 MPa和0.35。将梁的一端进行完全固定约束，在悬臂梁上施加不同的载荷和位移，分别模拟：1）不同半径悬臂梁在相同荷载作用下的工况，见图4(a)；2）同一半径悬臂梁在不同荷载作用下的工况，如图4(b)所示；3）对悬臂梁施加双向位移的工况，见图4(c)。

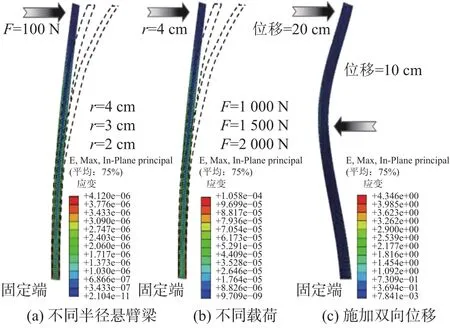
图4 不同工况下的数值模拟

通过有限元分析，获得悬臂梁表面沿长度方向的应变值，采用共轭梁法将应变值计算为位移值。计算出的位移值与Abaqus中直接输出得到的位移值进行比较。对比结果如图5、图6、图7所示。

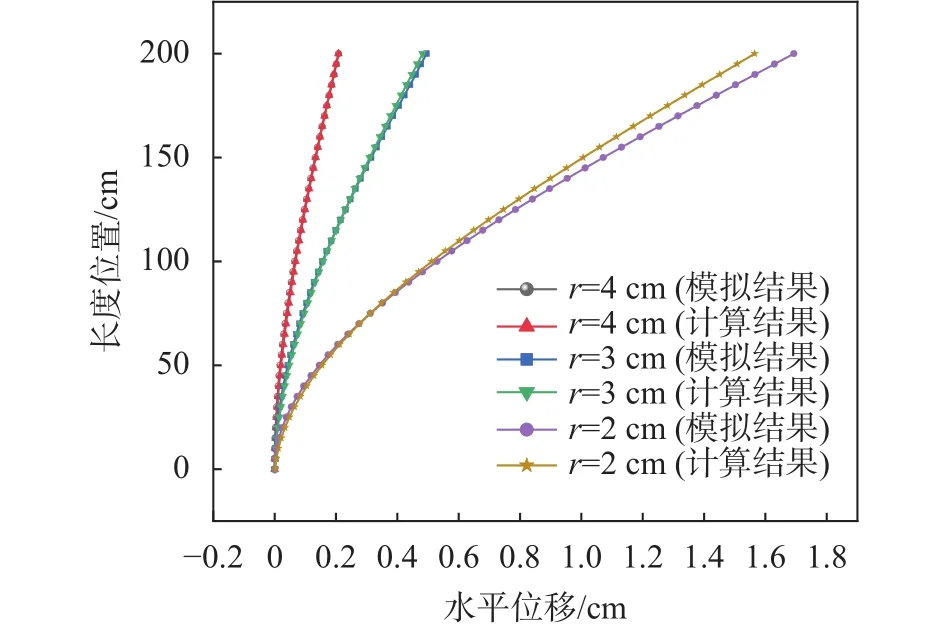
图5 相同荷载作用下不同半径悬臂梁的计算位移与模拟位移比较

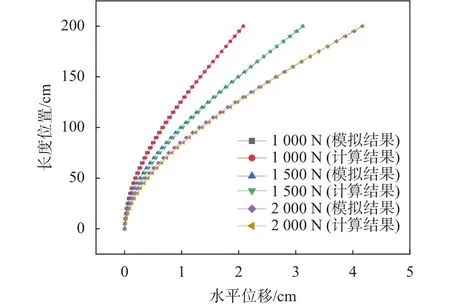
图6 不同荷载作用下同一半径悬臂梁的计算位移与模拟位移比较

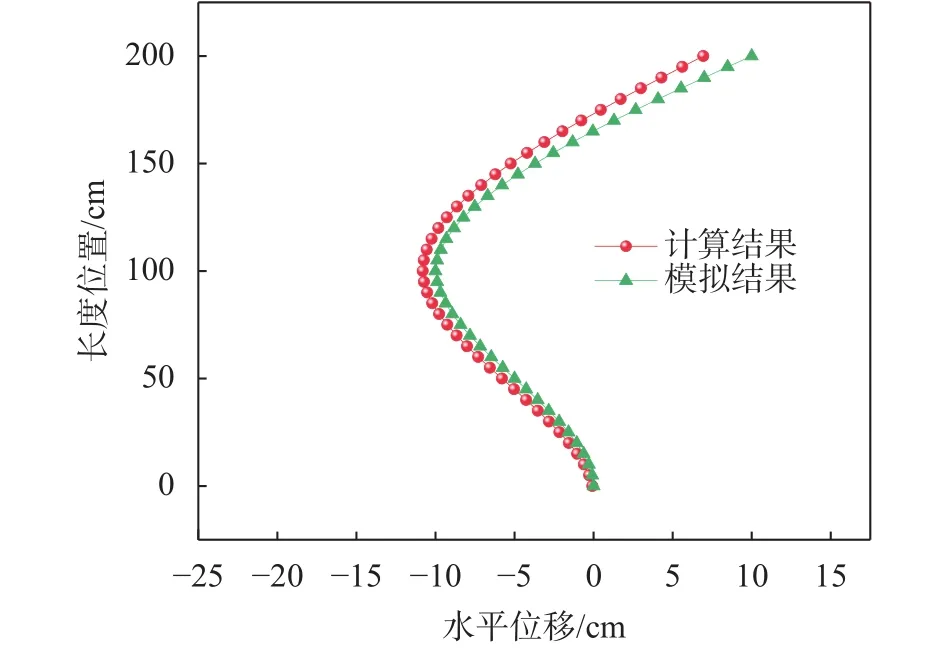
图7 双向弯曲下计算位移与模拟位移的比较

结果表明，共轭梁法计算的位移与有限元法计算的位移一致。在荷载不变、半径变化的工况下，三组最大误差分别为 0.01 mm/m、0.07 mm/m、0.64 mm/m。随着半径的减小，误差会逐渐增大，因此在该测斜仪设计制作时应对半径进行控制，但该工况的对比结果仍可说明该算法的可靠性。在半径不变、荷载变化的工况下，三组最大误差分别为0.15 mm/m、0.22 mm/m、0.29 mm/m，具有较高的精度。在施加双向弯曲位移时计算结果与模拟结果吻合较好。不同工况下模拟和计算的对比结果说明共轭梁法将应变转化为位移的准确性，并验证了可将该方法用于OFDR原位测斜仪，根据测得的应变计算测斜仪的变形。

3 校准实验

3.1 校准装置和方法

基于共轭梁法的OFDR原位测斜仪在进行边坡模型实验前，需要提前标定。标定装置如图8所示。该标定装置主要由钢架、OFDR原位测斜仪、位移螺母、夹具和位移计组成。钢架起整体支撑作用。钢架底部横梁上有一个固定夹，可以固定OFDR原位测斜仪（PVC棒）的一端，模拟固定端的边界条件。中间横梁有导向槽，用于控制OFDR原位测斜仪（PVC棒）在二维平面内的变形。右端的位移螺母可以上下移动。实验过程中，转动螺母使位移杆左右移动，从而对测斜仪的不同部位施加力和位移。用磁性底座将误差为0.01 mm的位移计固定在规定的高度，测出测斜仪的实际水平位移。不考虑温度与应变的交叉敏感性，在测试过程中，OFDR原位测斜仪长度1 m，每隔1 cm取一个点进行测量，传感杆上1 m长的光纤共有100个应变测点。通过共轭梁算法将得到的应变值转换为位移，并与百分表各点测量的实际位移值进行比较。

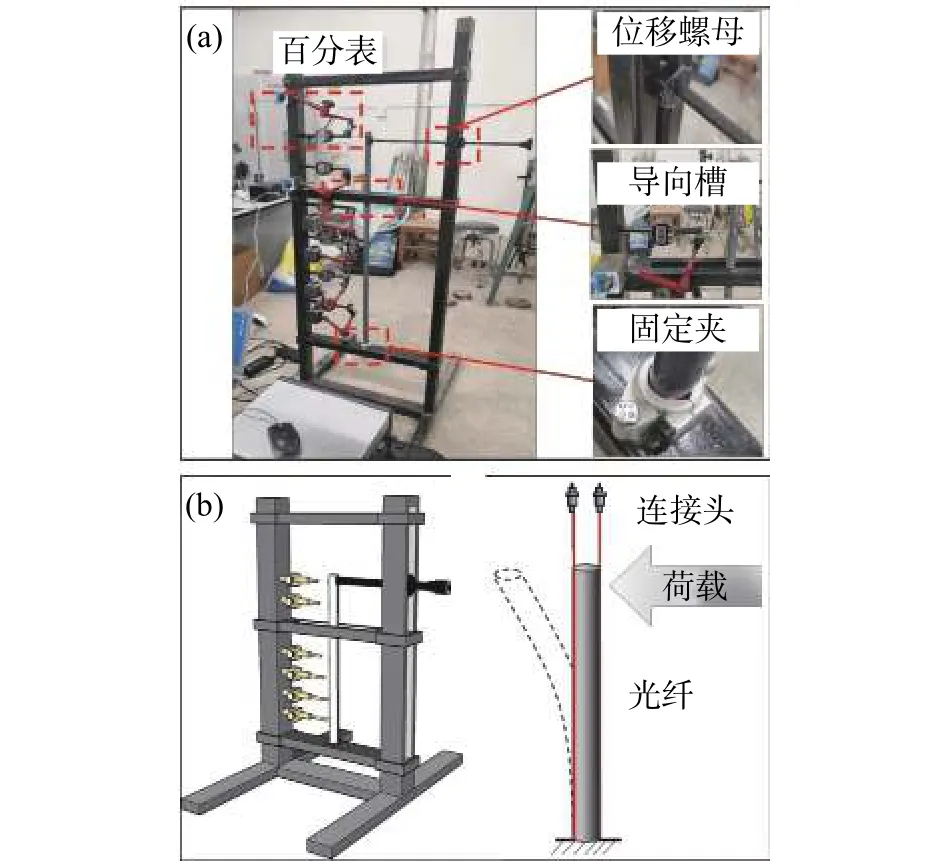
图8 标定实验

除此之外还采用了FBG原位测斜仪与OFDR原位测斜仪进行了对比，FBG测斜仪长度为1 m，每隔25 cm一个测点，共有4个测点。将FBG测斜仪测得的位移值与OFDR测斜仪测得的位移进行对比，验证OFDR测斜仪的测量精度。

3.2 标定结果

为方便测试结果的直观对比，将测量结果绘制为测点位置与水平位移的关系，如图9所示。从图9可以看出，基于共轭梁算法的OFDR原位测斜仪的测量值与百分表提供的参考值非常接近，并且相比于FBG原位测斜仪OFDR原位测斜仪测量结果更加精确。对测量的结果进行统计，采用相对误差(RE)、平均相对误差(MRE)和均方根误差(RMSE)对标定结果进行了分析，结果见表1。OFDR原位测斜仪测量结果的标准偏差为0.441 mm，相对误差为-9.66% ～ -1.18%，在允许的测量要求范围内。综上，在实验室条件下验证了所提测量技术的可行性与可靠性。这种技术在实际条件下的可用性与在实验室条件下的差别不大，但是光纤的连接、断裂、光弯曲损耗以及光纤的粘接或埋入工艺和传感棒材料等因素都会影响光纤的信噪比和测量不确定度，这将是下一步的研究重点。

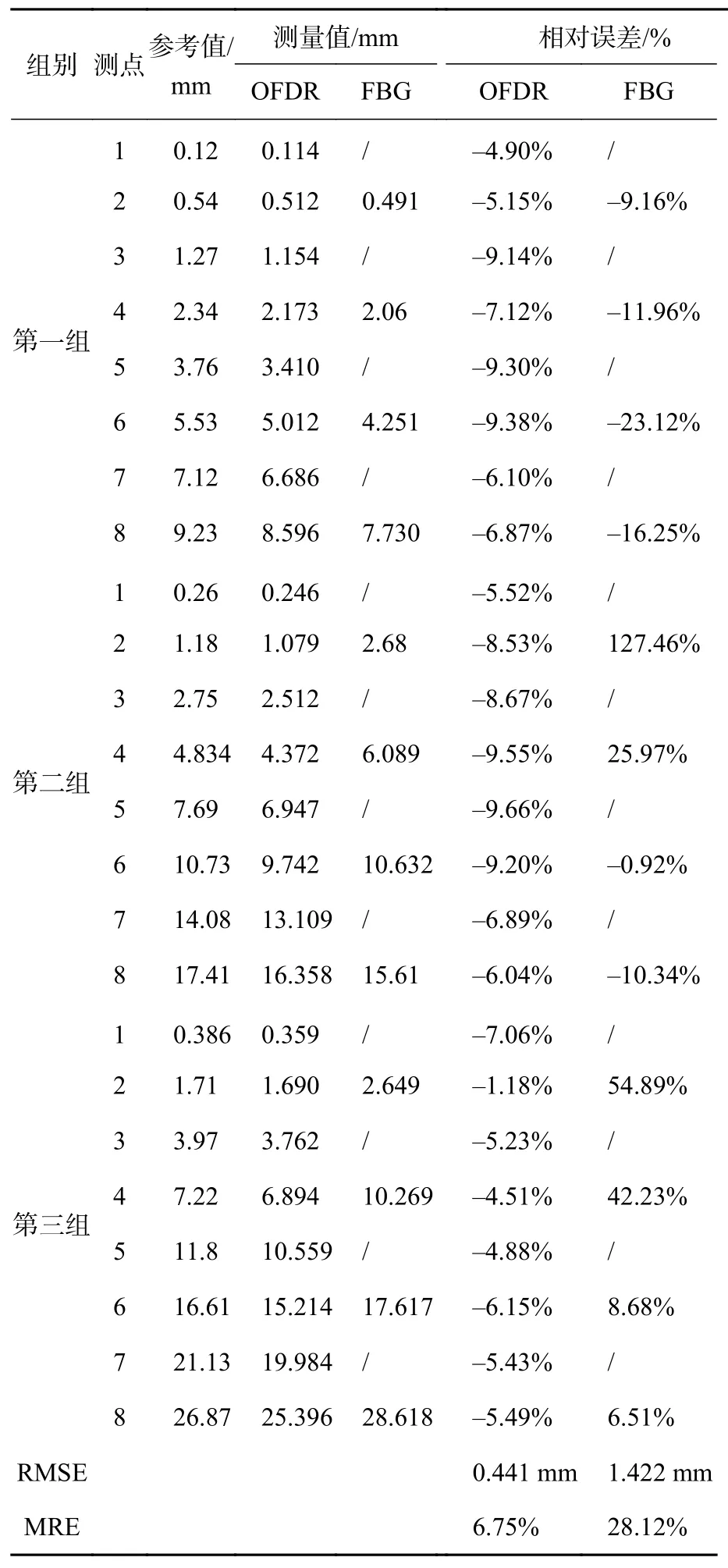
表1 实验测量结果统计

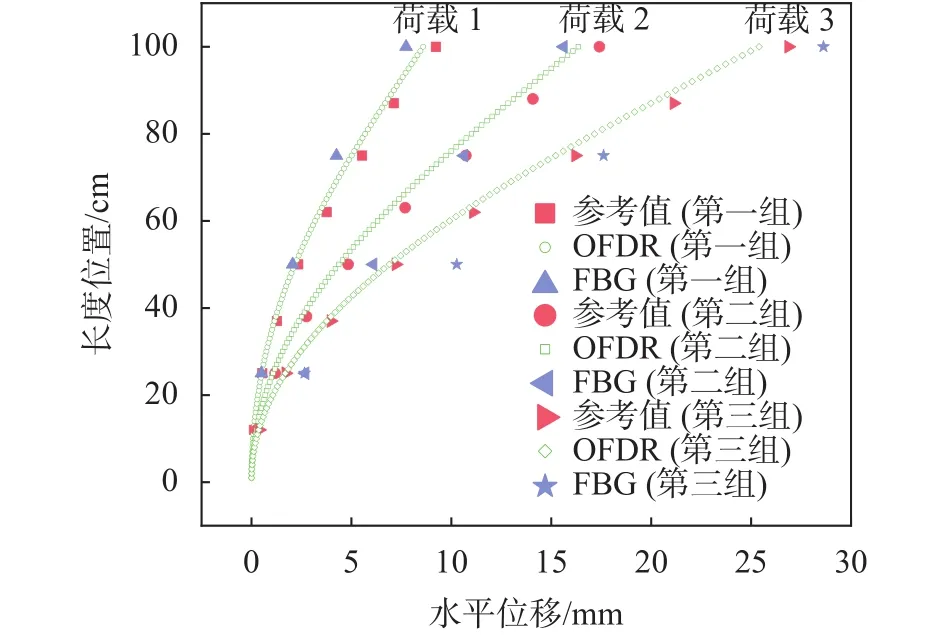
图9 位移计测得的变形与使用共轭梁算法得到的计算位移的比较

4 模型实验

为验证OFDR原位测斜仪的可靠性和实用性，进行了1g条件下的边坡模型试验。此外，还使用北京中弘泰科生产的误差0.1 mm的RT-1010测斜仪测量边坡的内部水平位移。最后，对两种测斜仪的监测结果进行了比较。

4.1 模型构建和加载过程

试验所用土样为标准砂与高岭土的混合物，按9∶1的混合比配制而成。本实验中使用的试验箱由钢制成，尺寸为长1 440 mm，宽640 mm，高800 mm，如图10所示。在填充模型边坡的过程中，采用分层压实方法。每次铺设厚度控制在5 cm，并进行压实，确保试验土具有良好的均质性。OFDR原位测斜仪和RT-1010测斜仪垂直安装在边坡的同一截面指定位置，下端固定，如图10所示。在试验过程中，为了研究OFDR原位测斜仪在边坡变形监测中的有效性，将液压千斤顶放置在宽160 mm、长600 mm的坡顶钢板上，利用液压千斤顶向坡顶逐级施加载荷。

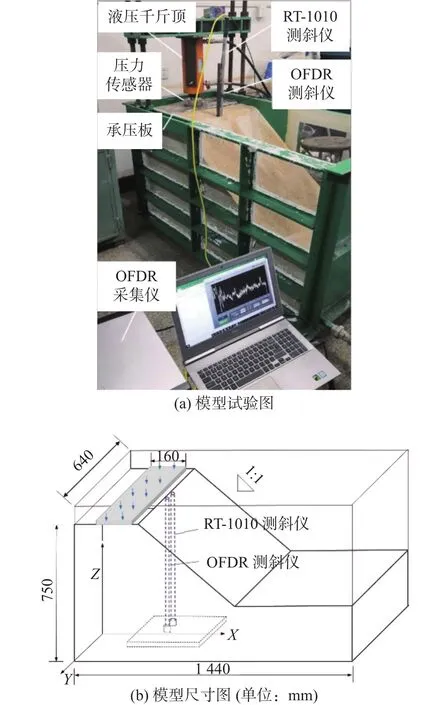
图10 边坡模型试验

4.2 实验结果

在边坡模型试验中，采用两种测斜仪对边坡内水平位移进行监测，监测结果如图11所示，两种测斜仪的测量结果具有良好的一致性。表明了OFDR原位测斜仪在边坡监测中的可靠性和实用性。随着高度的增加，位移逐渐增加。这主要是因为滑动面以下的土体相对稳定，变形较小，而滑动面以上的土体变形更明显。当产生较大变形时，OFDR原位测斜仪的测量结果与RT-1010测斜仪的测量结果会有一些偏差，主要是因为OFDR原位测斜仪的位移算法基于小变形假定，随着变形增大测量会有一定误差，但是测量精度仍能够满足工程测量要求，具有一定的工程实用性。如何解决大变形测量将是下一步的研究重点。

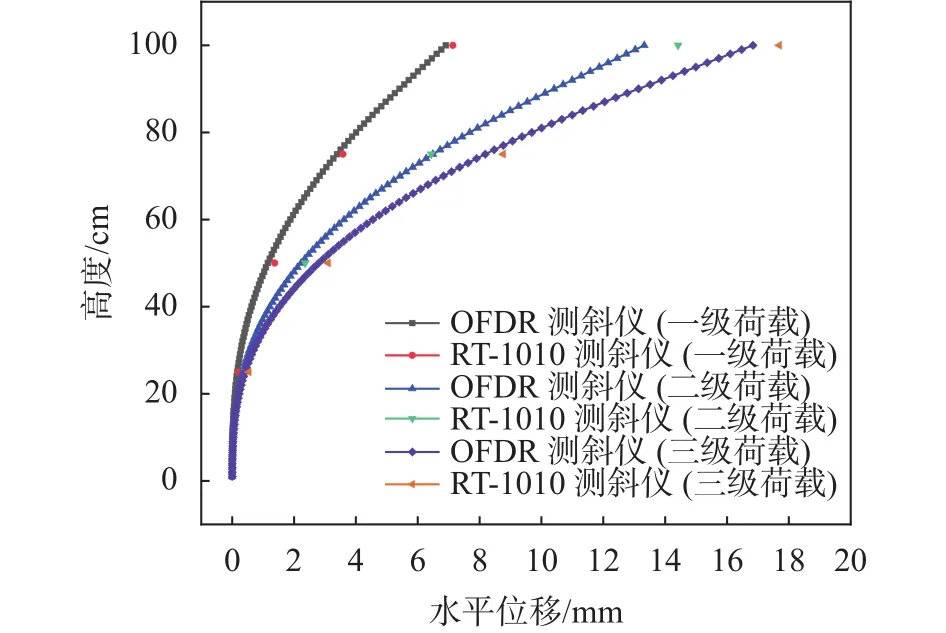
图11 两类测斜仪的测量结果

5 结束语

本文借助分布式光纤测量的技术优势，开发了一种基于OFDR技术可用于边坡深部水平位移监测的测斜仪。基于共轭梁算法推导了光纤应变与测斜仪位移的关系。通过有限元模拟，验证了共轭梁算法用于测斜仪位移计算中的有效性，并通过标定校准实验验证了OFDR原位测斜仪的有效性和精度。具体结论如下：

1）基于梁应变和挠度之间的关系，可使用分布式光纤技术测量土体内部的变形。室内实验表明，利用分布式光纤计算梁挠曲变形的方法简单，并可实现1 mm一个监测点的分布式测量。测试得到的位移与百分表测量的实际位移非常接近，该方法测量精度高，输出稳定，实验相对误差在±10%以内。

2）相比于FBG原位测斜仪，基于分布式光纤的OFDR原位测斜仪每毫米取一个测点，测点间隔更小，应变测量精度为1 µε，位移测量精度更高。同时较小的测点间隔更能准确捕捉边坡滑裂面的位置。

3）将OFDR原位测斜仪应用于边坡模型实验中，监测结果与传统测斜仪监测结果一致，说明了OFDR原位测斜仪于实际监测中具有一定的可靠性和工程实用性。