不同敷设环境下高压交流海底电缆导体温度和载流量的计算分析

李 娜，杨 昊，李 凯，李永健

（华北电力大学 机械工程系，河北 保定 071003）

0 引言

海上风电机组的投运，要求用于长距离海上输电的高压交流海缆具有安全性和稳定性。从建设成本，技术可行性等方面考虑，三芯交流海缆的应用前景更为广阔[1]。目前，已有三芯220 kV光纤复合海缆投入使用[2]。

海底电缆有铺设和埋设2种敷设方式。

铺设方式适用于远海和深海情况。该方式的特点是：可以节约成本；电缆外表面与海水直接接触。

为避免人类活动影响，在近海常用埋设方式敷设海缆。此时，海底电缆产生的热量通过海底土壤和海水传导，会造成不同敷设环境下海底电缆的温度差异，工作中海底电缆的持续发热和热量累积会使电缆升温。长时间且过高的导体温度将导致交联聚乙烯绝缘材料的失效、电缆使用寿命的降低、电缆载流量的受限。因此，关于不同敷设环境下电缆导体温度和载流量的精确计算具有重要意义。

针对电缆温度场和载流量计算，目前广泛采用的方法是基于有限元法的数值模拟方法[3,4]。此类研究的对象多为电缆沟敷设的电缆，研究主题多为电–热，热–流，电–热–流（空气）[5-8]。文献[9]使用多物理场数值分析软件准确计算了沟槽电缆的载流量；结果表明，由于沟槽内存在空气对流散热，沟槽敷设方式下的载流量相比直埋和排管敷设提高了30%和51.9%。文献[10]利用COMSOL有限元软件建立电磁–热–流耦合模型，分析了海底电缆沟内不同敷设方式对载流量的影响。文献[11]利用有限元法准确计算了海底电缆的载流量。文献[12]通过有限元仿真软件建立了电缆温度场和流场耦合仿真模型，得到了直埋敷设、排管敷设和沟槽敷设下电缆分别在3种直流拓扑结构运行时的直流载流量、温度分布和流场分布。文献[13]分析了敷设与埋设 2种情况下直流海缆的温度与载流量、海水温度的关系，提出了海水流速影响因子。在现有研究成果中，关于从整体考虑海水温度、流动及埋设深度对海底电缆温度场和载流量影响的分析较少。

本文以某近海风电项目所使用的三芯220 kV光纤复合海缆为研究对象，建立了海缆及敷设环境的二维仿真模型；利用该模型进行电磁–热–流耦合计算分析，研究铺设、埋设2种敷设方式下不同海水温度、海水流速、载流量对导体温度的影响并提出相关经验公式。

1 多物理场控制方程与耦合机理

电磁–热–流场的相互耦合机理如下：海底电缆通电后产生电磁场，导体与绝缘材料产生电磁损耗，由损耗产生的热量会改变周围的温度场；导体的线性电阻率与温度有关，温度改变会反过来影响电磁损耗和电磁场；电缆产生的热量经由土壤沙石和海水流动传递进而改变附近环境的温度；海水的密度因温度场变化而变化，进而影响海水流动。模型边界的海水通过对流传热收敛温度场。经过一定时间，电缆及其敷设环境的温度将达到稳态。

通过多物理场耦合系统，可以模拟海底电缆在不同敷设环境下的运行状态。电缆导体中的电流、导体的焦耳热与磁滞损耗、固体与流体的传热的控制方程和耦合方程如下。

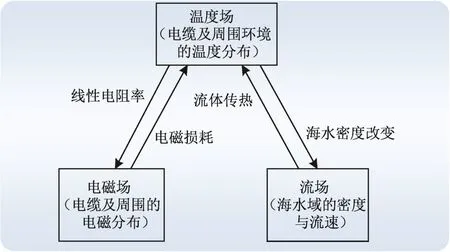
图1 电磁–热–流多场耦合机理Fig. 1 Electromagnetic-thermal-flow multi-field coupling mechanism

电磁场控制方程为：

式中：E为电场强度矢量；ω为交流角频率；A为磁矢势；H为磁场强度矢量；J为电流密度矢量；B为磁感应强度；σ为电导率；D为电位移矢量。

电磁–热耦合模块方程为：

式中：ρ为材料密度；C为材料常压下的比热容；Qe为总电磁损耗；Qrh为电阻损耗；Qml为磁滞损耗。

假设电缆中金属导体的电阻率线性变化，其计算公式为：

式中：σ为材料目前温度的电阻率；ρ0为材料在20 ℃时的电阻率；α为材料的电阻率温度系数；T为材料的温度；Tref为参考温度。

有热源的固体二维传热控制方程为：

式中：ρ2为固体材料密度；C2为流体材料常压下的比热容；k为导热系数；Q2为固体的热源。

有热源的流体二维传热控制方程为[14]：

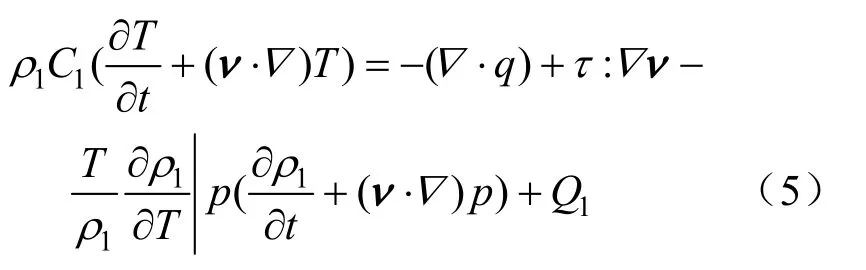
式中：C1为流体材料常压下的比热容；T为各部分的温度；q为传导热通量；τ为粘滞应力张量；Q1为流体的热源。

流场控制方程为[15]：

式中：ρ1为流体材料密度；v为速度矢量；p为压强；μ为动力粘度；I为单位矩阵。

2 海缆电磁–热–流耦合场建模

2.1 电缆模型及参数

本文研究对象为三芯220 kV光纤复合海缆，型号为HYJQF41-F127/220 kV×500。电缆结构见图2，结构参数如表1所示。

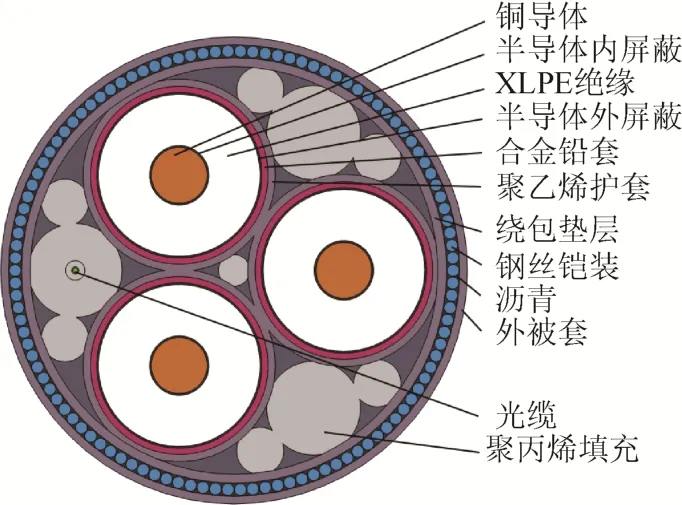
图2 三芯电缆模型Fig. 2 Three core cable model

表1 电缆结构参数Tab. 1 Cable structure parameters

计算之前需对求解区域进行网格划分。整体求解域采用三角形网格划分。由于电缆及周围的温度梯度、电磁场和流速变化较大，因此电缆区域网格较细密，远离电缆的区域网格较稀疏。最小单元大小为0.003 m，最大单元大小为0.67 m。有限元模型的网格划分如图3所示。

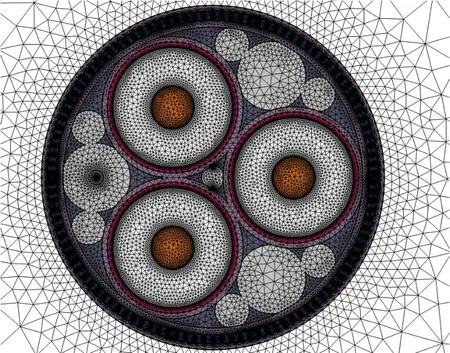
图3 模型网格划分示意图Fig. 3 Schematic diagram of model grid division

考虑距离电缆2 m以外的区域温度已不受电缆发热的影响[16]，因此，本文将求解域设置为10 m边长的正方形区域。如图4所示，海缆敷设环境分为水域和土壤域2个矩形区域：上方海水区域高 3 m，水域左侧为海水进口，右侧为出口以模拟海水流动；下方土壤区域高 7 m。铺设时，电缆在土壤表面，电缆中心距离土壤表面0.1 m；埋设时，电缆中心距离土壤表面距离d的取值范围为 0.3 m～3.9 m[17]。

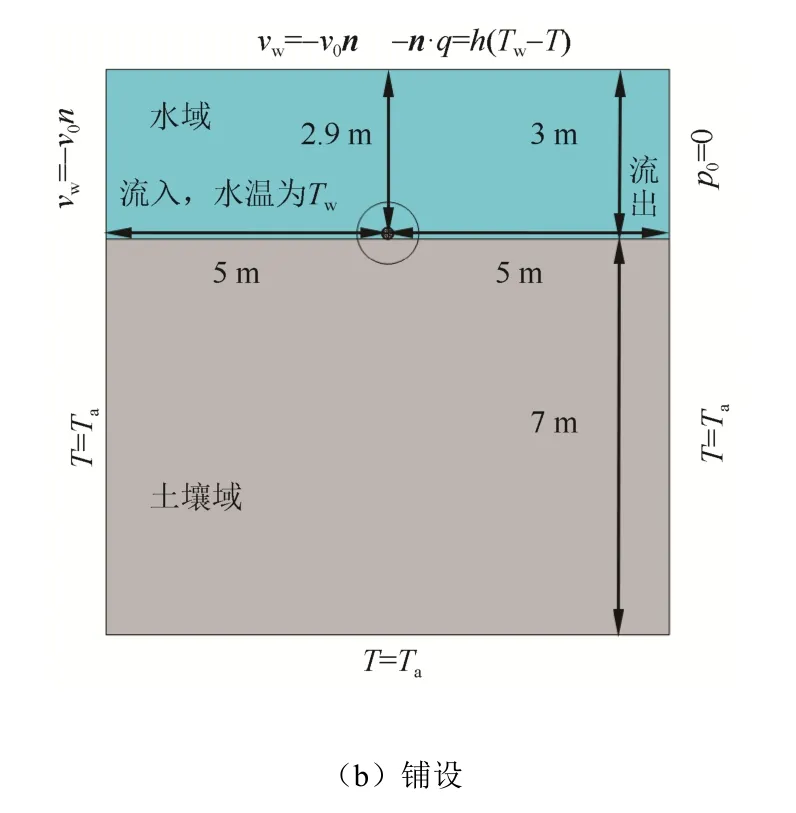
图4 海缆及敷设环境模型Fig. 4 Submarine cable and laying environment model

2.2 边界条件

设定水域上边界为对流热通量：

式中：n为单位方向向量；h为传热系数，设定为固定值6.5W/(m2·K)[18]；Tw为外部海水的温度；T为海水的温度。

设定水域左边界为水流入口，海水从左至右流入：

式中：v0为水流入口速度。

设定水域右边界为水流出口，压强

设定水域上下边界水流速度为0，即无滑移条件[19]。

设定土壤域左右下边界为固定温度值为20 ℃，土壤导热系数为1 W/(m·K)。

3 计算结果与分析

3.1 温度场、流场分布

实验设定：海水温度为20 ℃，海水的流速为0.2 m/s；给海缆加载的额定载流量为926 A；埋设时，深度为1 m。

XLPE绝缘材料最高耐受温度为90 ℃。考虑到绝缘材料与导体直接接触部分易因高温而损坏失效，因此导体温度的工作温度应尽可能控制在90 ℃以下。

电缆整体温度分布如图5所示。由图5可以看出，导体的温度最高，其余部分的温度沿着边缘方向递减。在敷设方式为铺设时，电缆外表面与流动海水接触，提升了海水散热效果，其导体温度较埋设时低。

图5 电缆温度分布图Fig. 5 Cable temperature distribution diagram

图6为环境温度分布图。从图6可以看出，在铺设时，电缆外表面温度与海水温度十分接近；埋设时，周围土壤因电缆发热而升温，距离电缆附近土壤区域温度高于环境温度。

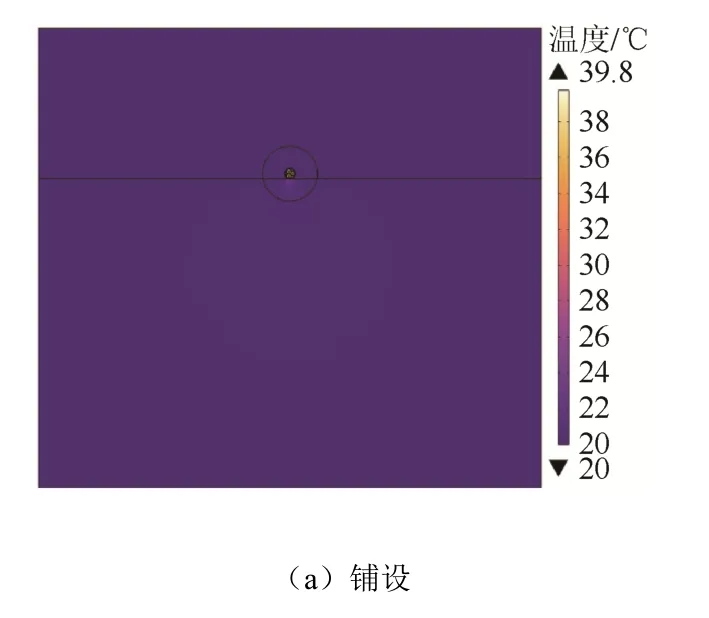
图6 环境温度分布图Fig. 6 Ambient temperature distribution diagram

图7为海水流速分布图。图7中，左侧为海水流入口，右侧为流出口。从图7可以看出，铺设时，电缆与土壤附近水流速度降低，铺设电缆右上方流速因漩涡现象增加；埋设时，电缆对于海水流速无影响。

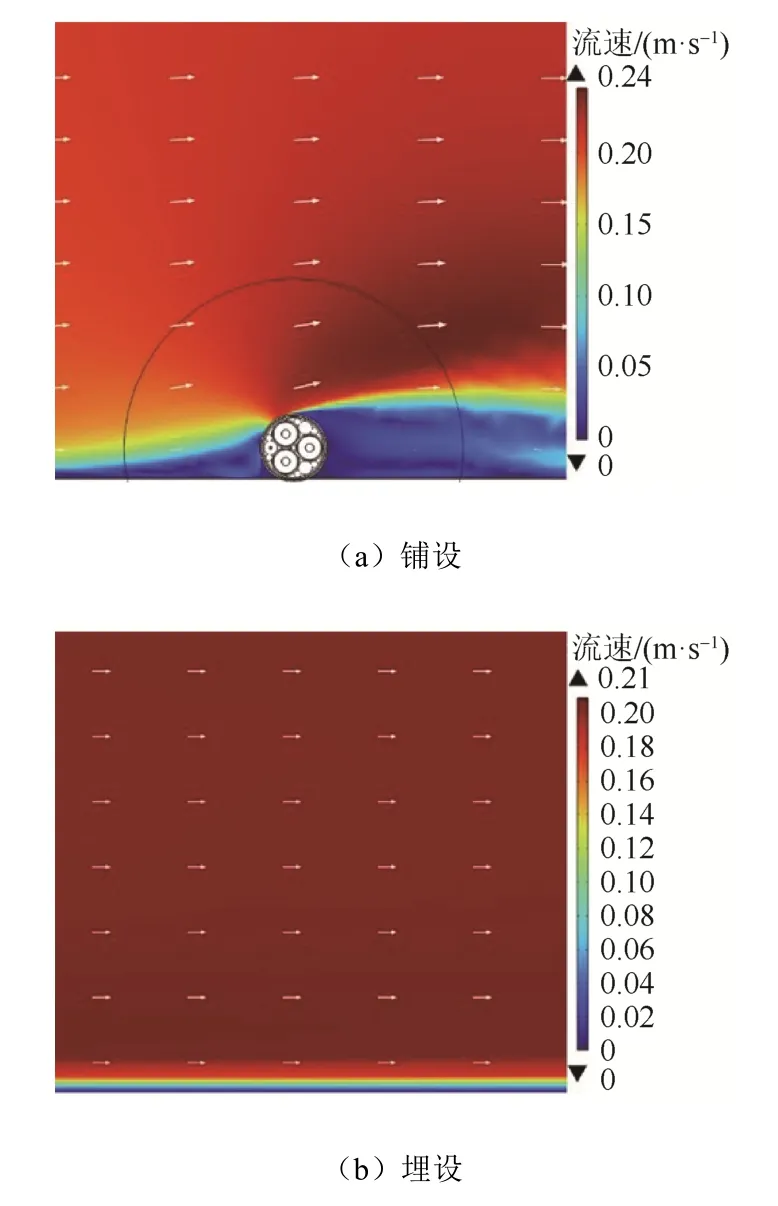
图7 海水流速分布图Fig. 7 Seawater velocity distribution

3.2 海水温度及流速对导体温度的影响

研究在铺设及埋设2种情况下，不同海水温度和流速对电缆导体温度的影响。

实验设定：海底电缆加载 926 A电流；在15 ℃～35 ℃温度区间内每隔2 ℃取一个值；在0 m/s～2 m/s流速区间内每隔0.2 m/s取一个值。

拟合得到不同海水温度及流速下，电缆导体温度分布如图8所示。当海水温度为15 ℃时，不同海水流速下导体温度如表2所示。由图8及表2可知：

图8 不同海水温度和流速下导体温度曲面Fig. 8 Conductor temperature surface under different seawater temperatures and flow velocities

表2 不同海水流速下导体温度Tab. 2 Conductor temperatures at different sea water velocities

（1）导体温度随着海水温度上升而上升。

（2）海水流动对海缆降温作用明显。当海水流速在0～0.02 m/s范围附近时，流速增大对导体温度有显著影响，散热降温作用明显增强；当流速大于0.02 m/s时，增加海水流速对导体温度的影响达到瓶颈。根据文献[20]，海水流速一般不低于0.02 m/s；所以可认为，在自然海流（流速0.1 m/s～1 m/s）[21]条件下，导体温度基本不受海水流速变化影响。

图9为铺设与埋设2种敷设方式不同海水温度下导体温度变化曲线。由图9可知：导体温度随海水温度上升而呈线性上升，且不同流速下斜率十分相近。

图9 不同海水温度下导体温度曲线Fig. 9 Conductor temperature curve under different seawater temperatures

令：铺设时，导体温度为Tcw1；埋设深度为1.1 m时，导体温度为Tcw2；海水温度为Tw。

得：铺设时，导体温度与海水温度相关系数为0.870 7；埋设深度1.1 m时，导体温度与海水温度相关系数为0.567 7。

于是，Tcw1、Tcw2与Tw的线性关系表达式如式（11）（12）：

不同埋深变化斜率如表3所示。

表3 不同埋深下a1和b1值Tab. 3 a1 andb1 values under different burial depths

分析表3数据：因铺设时电缆直接浸泡在海水中，导体温度随海水温度的增长速度比埋设时高；随着埋设深度的增加，电缆的热量需要途经更深的土壤层才能向海水传导，所以导体温度随海水温度变化的斜率a1逐渐降低。

3.3 埋设深度的影响

埋设时，海底电缆的散热效率与深度有关。图10为埋设时不同埋深下导体温度曲线。由图10可知：（1）导体温度随埋深增加而呈指数函数形式增长，斜率逐渐降低。（2）当埋深小于2 m时，导体温度增长速度较快。（3）当埋深大于2m时，导体温度增长速度较慢。这表明，海水温度变化对深层电缆导体温度的影响较小。

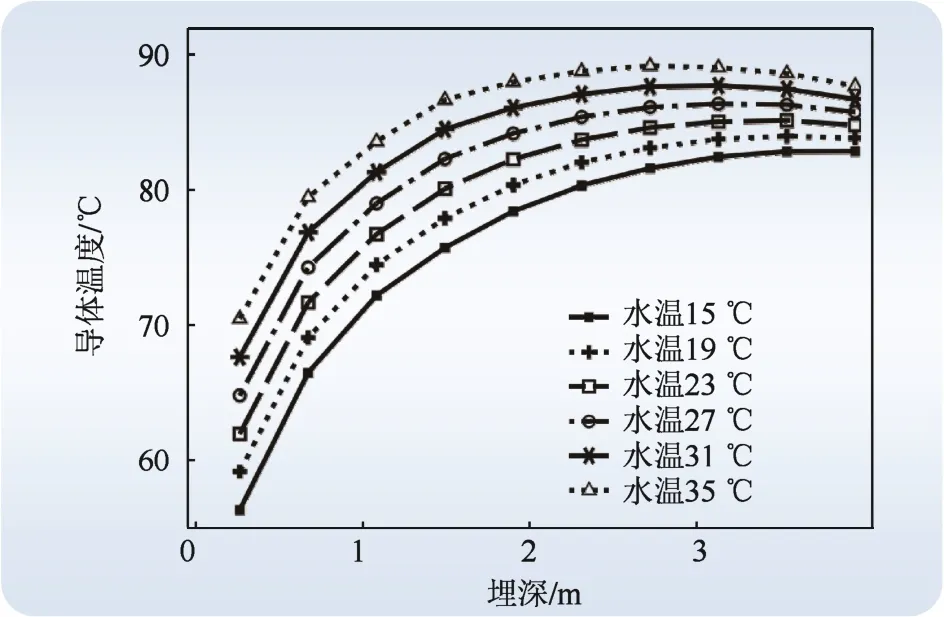
图10 不同埋深下导体温度曲线Fig. 10 Temperature curves of conductor under different burial depth

令导体温度为Tch1，埋深为d。使用龙格–库塔法对曲线拟合，得出Tch1与d的指数函数表达式，如式（13）和表4所示。

表4 不同埋深下a2、b2和c2值Tab. 4 a2,b2 andc2 values at different burial depths

由式（12）、图9和表3可知：不同埋深下海水温度与导体温度保持线性关系；相关系数a1随埋深增加而减小，截距b1随温度增加而增加。

由式（13）与图10可知，a1、b1的变化曲线符合一定规律，使用龙格–库塔法分别对a1、b1进行二次多项式拟合和指数函数拟合，分别得到a1、b1与埋深d的关系式（14）（15）。

由式（12）（14）（15）可得，在额定电流、埋设条件下，导体温度Tc1与海水温度Tw和埋设深度d的关系如式（16）所示：

3.4 载流量对导体温度的影响

在加载电流500 A～1 500 A区间内每隔100 A取一个值。不同载流量对海底电缆导体温度的影响如图11所示。

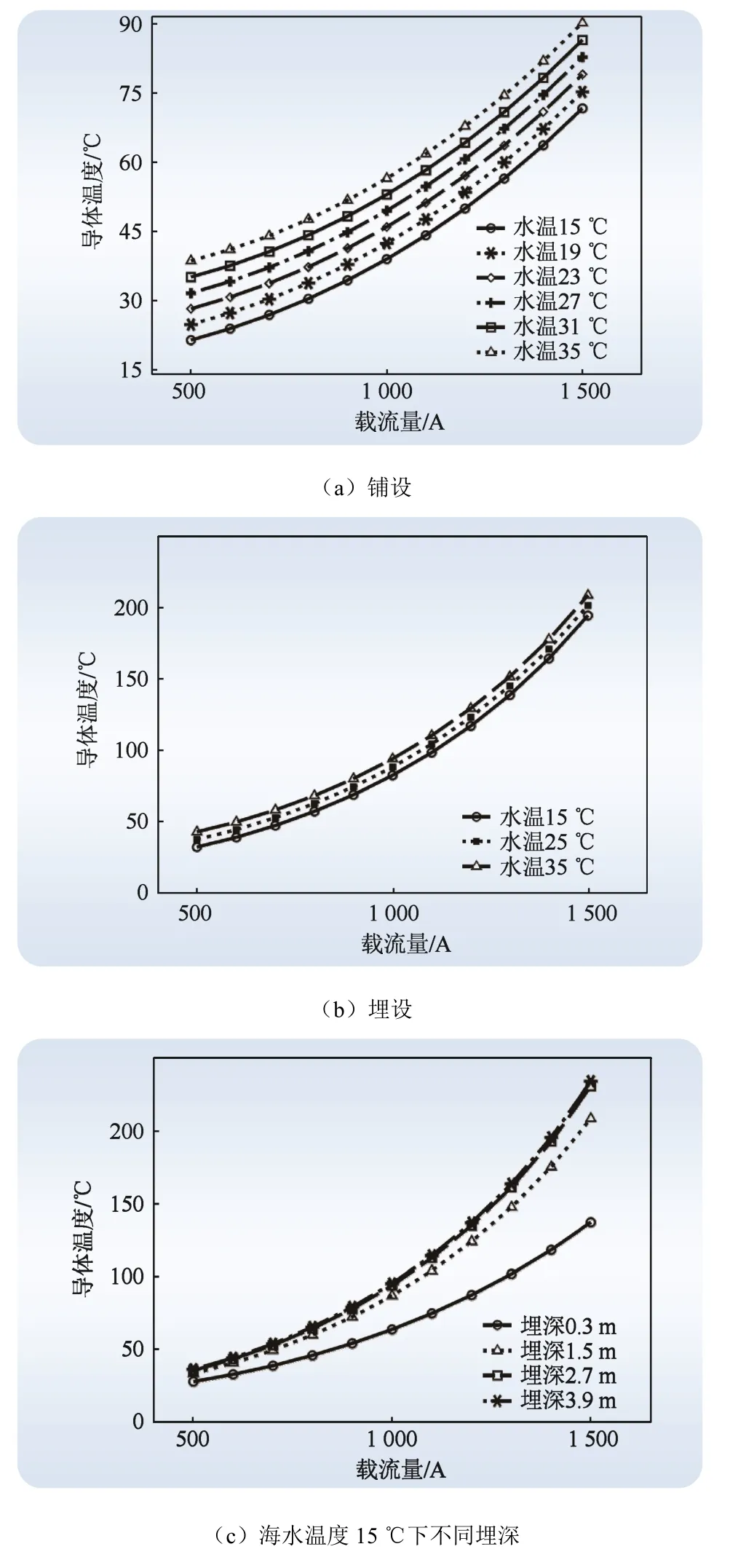
图11 不同载流量下导体温度变化曲线Fig. 11 Temperature change curves of conductor under different current carrying capacity

图11（a）（b）分别为铺设和1.1m深埋敷设时，不同载流量和海水温度下导体温度的变化曲线。由图可知：因铺设海缆与流动海水直接接触，其升温幅度远小于埋设情况；在不同载流量下，海水温度与导体温度仍保持线性关系，相关系数a1基本保持不变；导体温度随载流量增加，且载流量越大其升温速率越快。

令铺设时导体温度为Tci1，埋设深度1.1m时导体温度为Tci2，海水温度为Tw，载流量为I。经拟合得出Tci1、Tci2与I、Tw的指数函数关系，如式（17）（18）所示。

图11（c）为海水温度15 ℃时，不同载流量与埋设深度下，导体温度变化曲线。由图可知：不同埋深时，导体温度与载流量有与式（18）类似的指数函数关系；不同载流量时，导体温度与埋深的函数关系与式（13）类似；埋深越大，导体温度随载流量变化的速率越快。

当海水温度为15 ℃时，令导体温度为Tci3，载流量为I，使用龙格–库塔法对曲线拟合，可得出Tci3与I的函数表达式，如式（19）和表5所示。

表5 不同埋深下a3、b3和c3值Tab. 5 a3,b3 andc3 values at different burial depths

使用龙格–库塔法对曲线拟合，可得出b3与埋深d的指数函数表达式，如式（20）所示。

a3、c3与埋深无特定拟合曲线。不同埋深下，a3的平均值为18.281 0，c3的平均值为–8.475 1。结合式（16）（18）（19）（20），本文提出埋设时的导体温度Tc与海水温度Tw、埋深d、载流量I的经验公式如式（21）所示。式（21）适用范围：海水温度15～35 ℃，自然流速0.02～2 m/s，常见埋深0.3～3.9 m，载流量500～150 0 A。

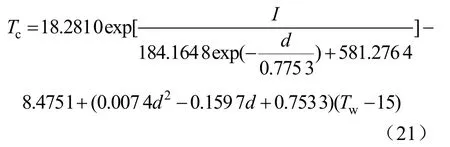
该式解析值与模型仿真值的部分误差如表6所示。由表6知，模型计算结果与经验公式计算结果的误差在5%以内。

表6 导体温度计算公式误差Tab. 6 Error of calculation formula of cable core temperature

4 交流海缆载流量预测方法

IEC 60287标准并未具体规定海水温度、流速、埋设深度与载流量的关系[22]。本文给出的式（17）（21）为铺设与埋设条件下的导体温度经验公式。当设定导体温度为90 ℃时，可分别得到计及海水流动下铺设与埋设时海缆载流量经验公式：式（22）（23）。该经验公式适用范围：海水温度15～35 ℃，自然流速0.02～2 m/s，常见埋深 0.3～3.9 m。

表7示出用4种模型计算得到的海缆载流量结果。第1种为本文建立的计及海水温度、流速、埋置深度的多物理场耦合模型；第2种为由耦合模型计算结果拟合得到的载流量经验公式；第 3种是不考虑海水流动的传统模型，其特点是模型边界温度为定值；第4种是利用IEC标准解析公式。传统模型和IEC标准并未考虑海水流速对电缆载流量的影响，其计算结果与海水流速变化无关。IEC 60287-3-1中提出典型高压电缆埋深为1 m，因此表7中埋设载流量结果均在埋深为1 m下求出。表7的结果在环境温度与海水温度均为20 ℃条件下计算得到。

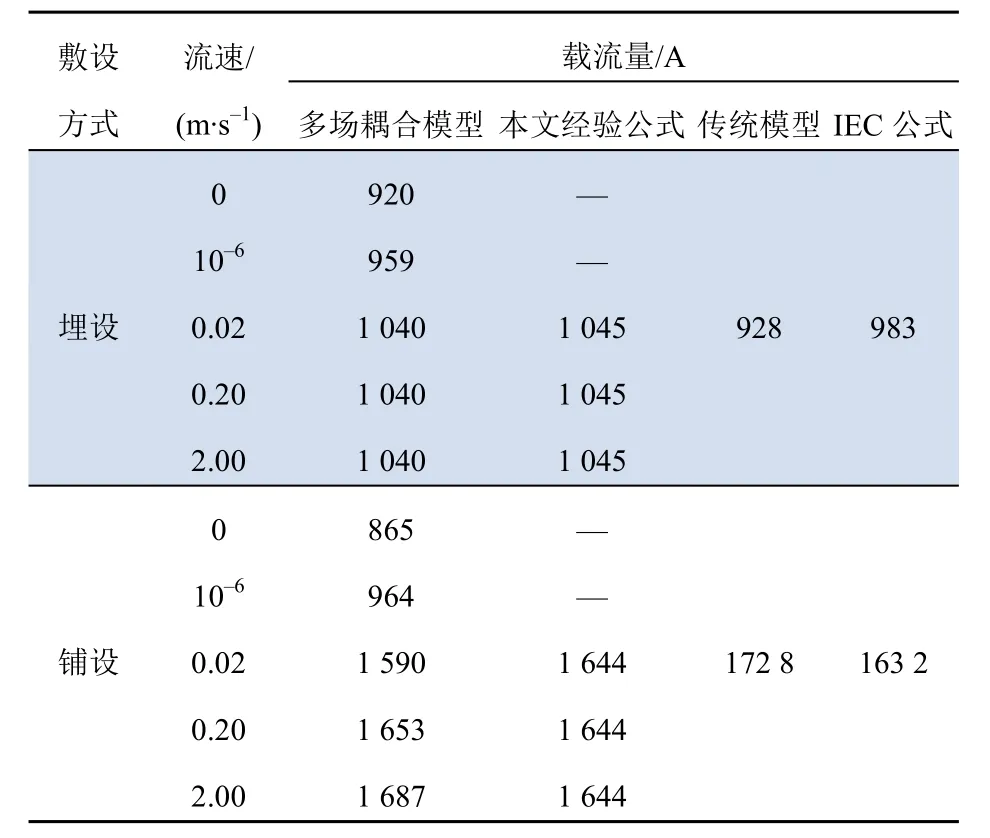
表7 4种方法载流量计算结果Tab. 7 Calculation results of current carrying capacity of four methods

表8示出了其中3种方法载流量计算结果与多场耦合模型的差异。

表8 3种方法载流量计算结果与多场耦合模型的差异Tab. 8 The difference between the calculation results of the three methods and the multi-field coupling method

结合表7、表8所示结果进行分析。

埋设时，海底电缆的热量通过土壤传导至海水和深处，海水流速对载流量的影响较小。在利用传统模型和IEC公式计算埋设电缆载流量时，默认海水流速为0 m/s（静止状态）。此时，传统模型、IEC公式预估载流量分别为920 A、928 A和983 A，多场耦合模型计算结果与另外2个模型分别相差8 A和63 A，相对误差为0.87%和6.84% ——结果十分接近。

铺设时，海底电缆的热量主要通过海水传导。此时，海水静止状态和流动状态的散热能力差别较大。对于铺设电缆，当采用传统模型与IEC标准解析公式进行计算时，通常直接将电缆表面温度值取作海水温度[23]，对应的多场耦合模型条件为自然海流流速（0.2 m/s）；此时多场耦合模型与传统模型、IEC公式预估载流量分别为1 653 A、1 728 A和1 632 A，多场耦合模型计算结果与另外2个模型分别相差75 A和21 A，相对误差为4.54%和1.27%——结果十分接近。值得注意的是，流速越接近于零，计算结果的差异越大；这说明，海水流速是计算电缆载流量时必须考虑的因素。

另外当流速大于0.02 m/s时，多场耦合模型与通过该模型得到的经验公式预估载流量的相对差异在 0.5%（埋设时）和 4%（铺设时）以内。在表6基础上，该结果进一步证明两者较好的一致性。

小结：本文多场耦合仿真模型能可靠地预测载流量；上述环境变量对导体温度的影响可信；载流量经验公式计算结果较为准确。

5 结论

本文建立了三芯交流海底电缆及敷设环境的电磁–热多场耦合二维有限元模型，研究了导体温度与海水温度、海水流速、敷设方式、埋深和载流量的关系，建立导体温度、载流量经验公式，现得出以下结论：

（1）导体温度与海水温度、海水流速、敷设方式和埋设深度有近似函数关系；环境因素对导体温度与载流量有显著影响，实际工程应用中不可忽视。

（2）通过本文模型在典型环境参数下得到的载流量，与传统模型和IEC标准计算模型的相对误差不超过7%。这表明，在不同敷设环境下，利用该模型计算海底电缆载流量结果的准确性。

（3）由模型计算结果建立的经验公式可反映导体温度与环境因素的函数关系，并能准确预估载流量。