融入社区评估的节点重要性分析

孙百兵，孙家政，何 泉，杜彦辉

1.中国人民公安大学 信息网络安全学院，北京 100038

2.中国人民公安大学 侦查学院，北京 100038

当前，世界正处在经济全球化的高速发展阶段，社会经济不断发展，随之而来也有竞争的加剧、新旧企业的更替，社会矛盾也在逐渐显现，群体性事件、团体活动不断增加[1-2]。公安机关面临的巨大维稳压力。为此，如何正确识别群体中起到关键作用的人物就显得非常具有研究意义。

随着社交网络分析研究的不断深入，各种各样的事务都可以被转化成社交网络，通过社交网络分析可以更好地了解事务的特征[3-4]。在实际生活中，将目标群体映射为社交网络，即使该网络拥有众多节点，节点间关系复杂，也可以通过节点重要性分析识别群体中起到关键作用的重要节点，把握住重要节点便可以掌控整个网络[5]。因此，如何准确、高效地对社交网络进行重要度分析有着广阔的发展前景。

目前节点重要性分析已经取得了很多研究成果。然而，现阶段的节点重要性算法很容易造成重要节点聚集的情况，这种情况也被称为“富人俱乐部”现象。造成这现象的根本原因是重要性算法的“重要节点的邻居节点也很重要”思想，该思想会造成与群体核心成员有直接关系的普通成员的影响力被抬高，而与核心成员没有直接联系但是也起到较大作用的其他成员的影响力会被相对压低，从而造成不客观的评价结果。针对此问题，本文分析目标群体网络的拓扑结构，将群体根据链路结构的疏密进行社区划分，评估社区在整个群体中的重要程度，并综合考虑节点在本社区的影响力以及其他社区的联通能力，提出了融合社区评估的节点重要性分析算法（node importance analysis integrated with community assessment，NI-CA）。

1 相关工作

关键节点是在整个网络具有较大影响的节点[6-7]，如何评价该影响力具有很多角度和方法，最经典评价指标有度中心性、特征向量中心性、介数中心性和K核分解等。近年来，国内外学者在经典算法的基础上不断完善改进，提出了很多新的评价方法。Bian等人[8]将多种评价指标与证据理论相结合，结合了多种算法的优越性，改进了算法性能。Zhang等人[9]将度值和K核值的结合作为定义节点初始权值，运用库仑定律融合度量节点在网络中的重要性。Li等人[10]结合了聚类系数与邻域内度值总和，提出聚类度的评价指标，提高了度中心性的准确度，但是也增大了计算的时间复杂度。Fei等人[11]研究认为节点的影响力与网络中其他节点有关，将目标节点的邻域与网络最短路径相结合，综合考虑每个节点与目标节点的相互关系得出影响力估值。Xu等人[12]针对目前大多重要性算法只针对静态网络的问题，提出能够面向动态网络的ALR算法，该算法将偏加权体系与Leaderrank算法相结合，提高算法在动态网络的适用性。Xu等人[13]认为节点的重要程度考虑其邻接信息熵，在加权网络用节点的强度来计算信息熵而在有向网络则综合了节点的入度和出度值。Yang等人[14]认为实际中的网络很多是在不断变化的，所以网络中各边的权重也在不断变化，提出了灰色关联和SIR传染病模型相结合的评价方法，对网络中的各个权重进行动态分配。Zhong等人[15]利用鲁棒性的思路，按照特定顺序删除网络中的节点，分析剩余网络的连通性等特征，并以此评估被删除节点的重要性。

2 基于社区评估的节点重要性算法

实际的社交群体中，具有较高影响力的人物或许具有一定的聚集性。但是在利用节点重要性算法进行理论分析时，这种聚集性被不断放大，导致具有较高影响力的节点都处于群体核心位置，而没有处于核心位置的节点影响力被过分低估，从而造成了“两极分化”的现象。由此可见传统算法在针对目标群体搜索重点人的应用上并不完善，据此，本文提出融合社区评估的节点重要性（NI-CA）算法。

2.1 社区评估

社区评估（community assessment，CA）是本文提出的衡量目标群体各社区重要程度的评价指标。本文根据社交网络的链路结构将目标群体进行社区划分，并根据各社区节点数量和平均路径长度分析其重要程度。

模块度是评价社区划分效果优良的关键指标[16]，一个好的划分结果其表现形式是：在社区内部的节点相似度较高，而在社区外部节点的相似度较低。模块度也是Louvain算法[17]的核心思想，Louvain算法是一种基于模块度高效社区划分算法，除了运算速度快、时间复杂度低，还有很高的准确度，不会遗漏小型社区。因此，本文采用Louvain算法对目标群体进行社区划分。

Louvain算法思想简单，是一个不断迭代和合并的过程，在这个过程中是否需要进行下一次是由模块度增益来确定的。网络中的模块度值计算方法如公式（1）所示：

其中，Aij代表节点i和j之间边的权重，Ki表示所有指向节点i的连边权重之和，Kj同理。δ(i,j)表示判断i与j是否为同一个社区，如果为同一个社区此值为1，否则为0。如一个节点从当前社区移动到另外一个社区时，图的结构就会发生变化，相应的模块度也会发生变化，把这种变化称为模块度增益，用ΔQ表示，计算方法如公式（2）所示：

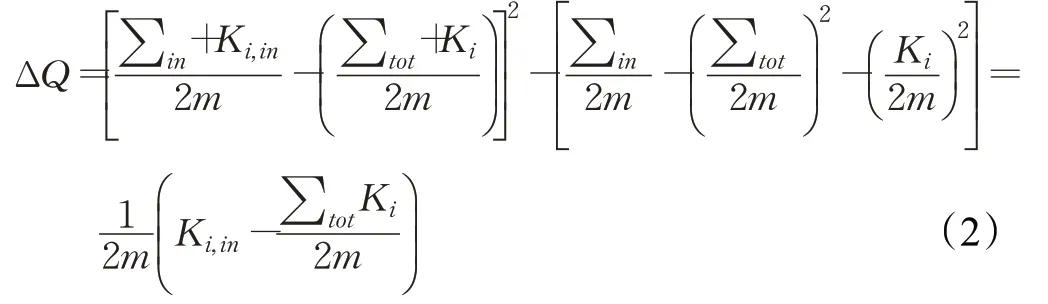
∑in表示在社区C中的所有边权值之和；C表示指点a要加入的社团；a表示将要移动的节点；Ki,in表示i点到C的所有边的权值之和；∑tot表示所有连接到社区C的边的权值之和。Louvain算法在初始的分区阶段有尽可能多的社区有节点。对每一个节点i，考虑将它加入到它的邻居节点j并计算模块度增量的变化，如果模块度增量变化大于0，则将它放到对应模块度变量变化最大的邻居节点，否则，该节点仍然保持在原来的社区，直至全网络没有可以分配的节点后停止迭代。

谭跃进等人提出了一种凝聚度的评估方式[18]，具有较高的准确性。目标群体网络的凝聚度取决于群体中各成员间的联通能力和群体规模，联通能力用网络的平均路径长度l衡量，群体规模用成员数量n衡量。对于有n个成员的目标群体网络G的凝聚度如公式（3）所示：

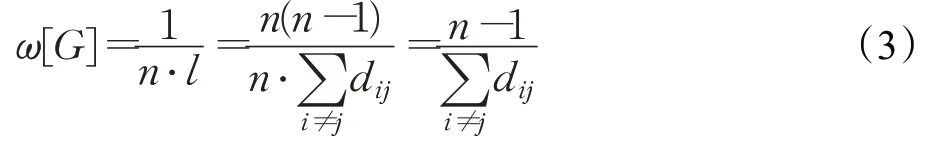
其中，节点i和节点j是目标网络的不同的两个节点，dij代表节点i和节点j之间的最短距离。当n＝1时，ω[G]=1。

本文运用Louvain算法将目标群体网络划分成t个社区，各社区分别用C1,C2,…,Ct表示。对网络社区分别进行重要性评估时，本文将需要评估的社区中的所有节点聚合为一个超节点，其他社区保持原样，C1,C2,…,Ct各社区分别聚合后形成的网络分别记为C1,C2,…,Ct，根据聚合后使得网络凝聚程度变化率评估社区重要性，在评估下一个社区时，原聚合的社区恢复成原本的拓扑结构，社区划分和聚合的过程如图1所示。

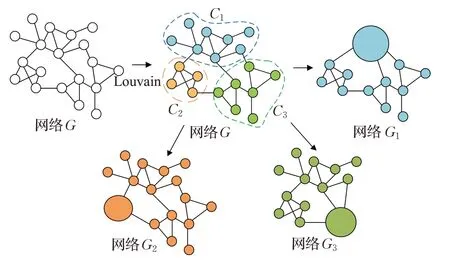
图1 社区划分和聚合Fig.1 Community segmentation and aggregation

定义1基于社区划分和凝聚度的社区评估（CA）可以进一步表示为公式（4），ω[Gi]的值表示Ci社区的重要度值。

2.2 基于社区评估的节点重要性算法

针对传统节点重要性算法的高影响力节点过度聚集的现象，本文提出的NI-CA算法在评估节点影响力时，考虑目标节点在其社区外部影响力的同时，融合该节点在其本社区的影响力。由于对目标群体网络进行社区评估，并且分析了目标节点的局域影响力，NI-CA算法可以在客观评价节点重要性的同时避免节点影响力的“两极分化”。

节点的社区内部影响力应当考虑节点在本社区的联通能力，由于介数考虑的是网络中所有最短路径的占比问题，因此介数中心性能够很好地反映点或边在整个社区中的重要性。本文引入介数中心性对节点内部的联通能力进行评价，其核心思想是认为的处于网络中间位置的节点相比于周边节点具有“更大的人际关系影响”。对于节点i的介数中心性（betweenness centrality，BC）的计算公式如公式（5）所示：

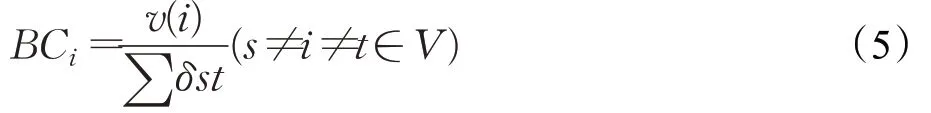
其中，v(i)表示经过节点i的最短路径个数，∑δst表示网络中是从顶点s到顶点t的最短路径数，V是网络G的节点集合。对于节点在其社区内部影响力评价，还应当考虑目标节点所在社区的整体影响力，社区评估的影响力越大，该社区领袖的影响力越大。

定义2社区成员的内部影响力（internal influence）用I表示，C1社区成员i的内部影响力如公式（6）所示，其中BCiC1表示节点i在其社区内部的介数中心性值。

在实际生活中，如果一个人在其他社区有很多朋友，他可以发挥重要的角色来接收和传播他的圈子周围的信息，因此本文在评估重要性时还要考虑该节点在其社区外部的影响力。

定义3社区成员的外部影响力（external influence）用E表示，节点i的外部影响力计算公式可以进一步表示为：

节点j是节点i的邻居节点，当节点j与节点i不属于同一社区时，aij=1；当节点j与节点i属于同一社区时，aij=0。CA(j)表示节点j所在社区的社区评估值。

定义4基于社区评估的节点重要性算法NI-CA，综合考虑目标节点在其社区外部影响力和该节点在其本社区的影响力，节点i的重要性度值可以表示为：

基于标准化欧氏距离的修正：

标准化欧氏距离公式是基于二维坐标的直线距离，可以消除在计算两因素时，其中一个因素数值过大从而压制另一因素的弊端。

2.3 NI-CA算法应用步骤

根据社交网络的拓扑结构分析成员重要度的研究，传统算法很容易得出高影响力成员“扎堆”的结果，而未处于网络核心位置的其他成员的影响力却相对被低估。以诈骗团伙为例，对于一个拥有几百甚至上千的团伙，团伙中的每个成员都有各自的分工，有指挥组、剧本组、一线电话组、二线电话组、倒卖电话卡组、洗钱组等。每个组都有该组中相对重要的成员，而根据传统节点重要性算法分析，重要成员大都集中在处于网络核心位置的指挥组，即使是指挥组中的只起到辅助作用的人员也会得出很高的影响力估值，而其他组中的起到一定作用的成员影响力被相对低估。针对这一问题，对一个已知目标人群的社交网络G=(V,E)，基于社区评估的NI-CA算法的应用步骤如下：

步骤1根据目标网络的拓扑结构，运用Louvain算法对网络进行社区划分，将群体划分为多个小群体。

步骤2对被划分后各社区进行重要性评估，分别聚合各社区节点，根据公式（3）和公式（4）计算出各社区在整个网络中的重要程度CA值。

步骤3根据目标节点所在社区的社区评估CA值和链路结构，通过公式（5）和公式（6）计算出目标节点的社区内部影响力，找出各社区的领导人。

步骤4考虑目标节点的跨社区联通性，通过公式（7）计算出目标节点的社区外部影响力。

步骤5将步骤3和步骤4的计算结果有机结合，通过公式（8）、（9）计算出目标节点的NI-CA值。

NI-CA算法流程如图2所示。

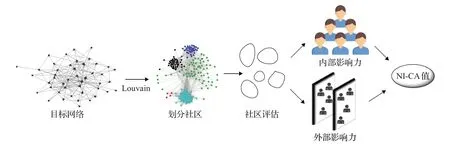
图2 NI-CA算法流程图Fig.2 Flow chart of NI-CA algorithm

社区评估（CA）的计算如算法1所示：

算法1社区重要性评估

输入：无向网络G=（V，E）

输出：各社区重要性度值CA(Ci)

1.将G中各个点初始化为一个社团，根据式（1）计算此时的模块性值；

2.for viin V

节点到其邻居节点所在的社区，根据式（1）、（2）计算模块度的变化ΔQ，若移动后致使ΔQ变化最大，则移动成功，否则保持不变；

end for

3.fori=1 to t/*t为社区个数）*/

将Ci社区分别聚合后形成的网络记为Gi；

根据式（3）、（4）计算各社区重要性评估值CA(Ci)；end for

4.return各社区评估CA值

基于社区评估的节点重要性（node importance algorithm based on community assessment，NI-CA）如算法2所示：

算法2节点重要性评估的NI-CA算法

输入：无向网络G=（V，E），各社区评估值

输出：网络中各节点重要度NI-CA值

1.统计各社区的网络拓扑结构；

2.for viin V

根据公式（5）、（6）计算目标节点在其社区内部影响力；

根据公式（7）计算目标节点与其他社区间联通能力；

根据公式（8）、（9）计算目标节点的综合重要性；

end for

3.return每个节点的重要度NI-CA值

3 实验与分析

3.1 数据描述

本文选取四个不同的链路网络进行验证实验，分别是空手道俱乐部（Karate）网络[19]、《冰与火之歌》（A Song of Ice and Fire）人物关系网络[20]、Facebook社交账号数据集[21]和中国某地区诈骗团伙（fraud ring）人物关系。其中Karate网络是最常用的复杂网络数据集之一，源自于美国一所大学空手道俱乐部的真实人物关系，在众多社交网络实验中被应用；A Song of Ice and Fire是美国著名长篇奇幻小说，其人物角色众多，关系复杂，适合作为实验数据；Facebook是目前最大的线上社交平台之一，可以代表线上交流网络进行实验；Fraud ring网络源自于已经侦破的网络诈骗犯罪案件（长兴县刘东等诈骗案与刘罗亮等诈骗案，详见裁判文书网（2020）浙0522刑初15、16号判决书），本文根据该组织的成员的职务分工构建链路网络，该案件系犯罪团伙的典型代表，案件清晰、判决明确，非常适合进行验证实验。以上四种网络的基本特征如表1所示。

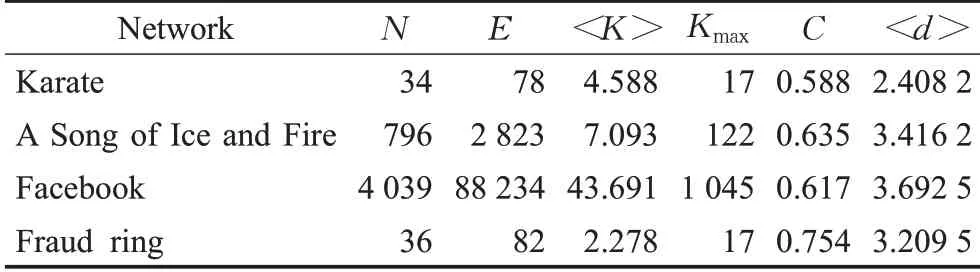
表1 网络数据基本参数Table 1 Basic parameters of network data

其中，N表示数据集中的节点数量，E代表节点间的边数，＜K＞表示数据集的度平均值，Kmax表示网络数据中节点度的最大值，C表示网络的平均聚类系数，＜d＞表示网络的平均最短路径。

3.2 实验设计及分析

本文的研究目的是根据拓扑结构，对群体网络中的成员进行重要性评价。为了验证算法的优越性，运用四个不同类型的群体网络作为实验数据，通过SI传染病模型、鲁棒性测试以及肯德尔相关系数进行验证，横向对比度指标（degree）、特征向量中心性（eigenvector）、介数中心性（betweenness）和PageRank的实验结果。Degree指标表示一个节点的邻居节点越多，节点的重要性越大；Eigenvector指标既考虑邻居节点的数量，也考虑邻居节点的重要性，是一种迭代的计算过程；Betweenness指标由经过目标节点的最短路径数目来刻画节点的重要性；PageRank算法最初用作互联网网页重要度的计算，后广泛用于节点重要性评估，它对每个节点赋予一个正实数，代表节点的重要度，经过随机游走模型，PageRank值越高，节点就越重要。

3.2.1 SI模型实验

SI传播模型[22-24]验证节点重要性准确度的最常用的方法之一，其中S表示易感染者（Susceptible），I表示已感染者（Infectious）。SI模型是将部分节点作为传染源（I状态），以β的概率不断传染与其邻近的易感染者（S状态）。

公式（10）所表达的含义为：对于网络中的状态为易感染S的节点i，如果该节点与感染状态I的节点j接触，节点i将会以β概率被传染，从而成为感染状态节点，成为新的感染源，更新状态为I(i)，而原感染状态I的节点j，状态不会再发生变化。此刻这些节点又成为新的感染源，感染网络中其他节点，直至网络中所有节点都变为I状态，传播过程结束。

由图3可以看出，当感染到达T时刻，SI模型的最终状态是网络中所有节点都感染为I类节点。因此，本文依托SI传播模型，衡量组织中具有重要角色的成员向其他成员传递其影响力的传播能力，并根据传播结果进行评价，传播越快、感染数量越多，则说明感染源节点对于其所在的网络重要程度准确性越高，即算法得出的网络重要节点排序越准确。

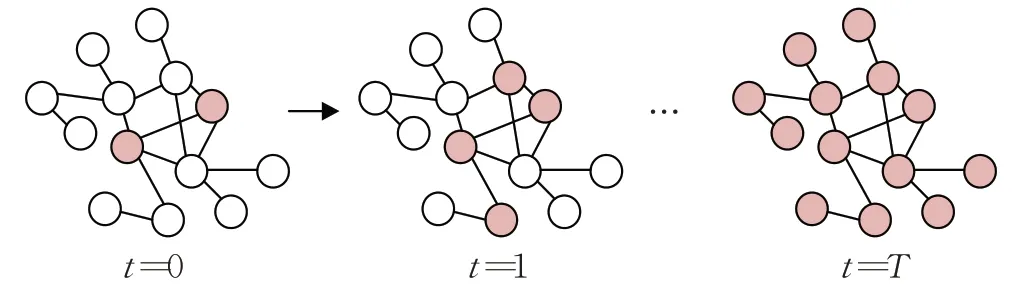
图3 SI传播过程图Fig.3 SI propagation process diagram

实验结果如图4所示，纵坐标为感染者的数量，横坐标为迭代次数。实验结果表明NI-CA算法的效果整体较好，在Karate网络和Fraud ring网络因为节点数较少，传播效果最为明显，各传播实验效果差别明显。A Song of Ice and Fire人物网络和Facebook网络节点数较多，传播结果的区分不明显，但是仍然能够看出在A Song of Ice and Fire人物网络中的传播效果最好，即在该网络中，NI-CA算法评价的重要节点具有更高的连通性，可以更快速地将信息传遍整个网络。在Facebook网络中的传播效果前期并不是最优，但是在中后期的传播速度明显提升，也就说明在Facebook网络中，NI-CA算法在计算各节点重要性时，最初评价效果并不突出，但是中后期对节点的重要性评价较为准确。传统节点重要性算法因为重要节点聚集，将这些节点作为传播源时，信息传播会大量出现重叠的情况，即花费太多时间重复将信息传播给聚集圈周围的节点。NI-CA算法通过社区评估找出不同社区的重要成员，并以此为传播源进行信息传播，由于信息源较为分散，所以传播至整个网络的速度更快，有效减少了信息传播重叠的情况。

图4 SI传播实验结果Fig.4 Experimental results of SI propagation

3.2.2 鲁棒性测试

鲁棒性指标[25-27]可以衡量某些节点在被移除后网络功能变化情况。在网络鲁棒性实验仿真中，按照节点重要度排序顺序依次移除节点。这样可以考察攻击一部分节点使之失去效果后，即移除该节点，网络整体结构和功能上的变化，用图中的最大连通分量中的节点数目与整个图中节点的总数目得到比值，作为衡量复杂网络功能鲁棒性的强弱。比值越接近1，说明整个网络中实现功能的结构体越大越完整，也说明鲁棒性越强。其计算方式如公式（11）所示：

L是表示最大联通分量，G为当前的图，θ随着被移除节点数i的增加而下跌如果该曲线下降的越快，则认为移除的节点越能使网络碎片化的程度越高。换句话说，如果依次移除通过节点重要性算法得到的节点序列可以使整个网络的碎片化程度越大，则这样的节点越重要，这个算法也就越好。

由于鲁棒性测试中，在依次移除节点时，移除到中后期的网络会非常分散，并且无法对比出各算法之间的优越性差异，所以本实验分别运用NI-CA指标、Degree指标、Eigenvector指标、Betweenness指标和PageRank的实验结果分别对四个不同的网络进行节点重要度计算，按照各种计算出的节点重要性排序依次移除各网络的节点，横向对比各算法之间的θ值。

鲁棒性实验结果如图5所示，横坐标为移除节点占比，纵坐标为最大连通分量规模占比。由于很多网络在节点移除后期剩下节点大多是单节点，为了实验效果的区分度，本实验将节点移除至最大连通分量规模占比低于0.1时结束实验。绘制曲线可以准确地得到移除节点对图的影响过程，从而间接衡量了节点重要性排序的效果。实验结果表明各算法在前期移除节点的过程中效果相差不大，但是在持续的移除过程中，各算法之间的差别逐渐显现。NI-CA算法的实验结果整体较好，但是在Karate网络中的实验效果并不突出，此外，在Facebook网络和Fraud ring网络的实验前中期效果显著，但是在实验后期效果较差。整体而言，按照NI-CA算法计算结果顺序移除节点，对目标网络的破坏性较大，移除后网络更加分散。传统节点重要性算法所形成的重要节点聚集现象，在鲁棒性测试中可以明显看出该现象的影响，当移除一个重要节点后，下一次移除的节点很可能是该节点的邻居节点，从而对网络的整体性破坏很小。NI-CA算法通过评估节点的社区内部、外部影响力，有效减少了重要节点聚集的现象，更快速地分散整个网络。

图5 鲁棒性测试结果Fig.5 Robustness test results

3.2.3 肯德尔相关系数验证

肯德尔相关系数τ[28-29]是一个用来测量两组序列相关性的统计值，在统计学领域多用于分布未知、数据类型离散的相关样本的比较，取值范围在-1到1之间，当τ为1时，表示两个随机变量拥有一致的等级相关性；当τ为-1时，表示两个随机变量拥有完全相反的等级相关性；当τ为0时，表示两个随机变量是相互独立的。由此可知，当通过算法得出的重点人排序与网络中真实的头部重点人比较时，肯德尔相关系数越大，说明和谐的节点数越多、算法效果越好。

其中，nc和nd分别表示和谐以及不和谐的个数，n为网络节点总数，公式（12）之所以用和谐与不和谐的个数差除n(n-1)÷2，是为了解决归一化问题。

本文选取Karate网络、A Song of Ice and Fire人物网络和Fraud ring网络进行肯德尔相关系数实验，通过网络结构背后的实际意义、剧情和主演列表以及中国裁判文书网对相关Fraud ring判决文书确定各网络的关键节点序列，分别运用NI-CA指标、Degree指标、Eigenvector指标、Betweenness指标和PageRank算法所计算出的重要成员进行相关性分析，横向比较各组数据的肯德尔相关系数。

四种网络的肯德尔相关系数验证结果如表2所示，实验结果显示，各算法对Karate网络节点的验证都较为准确，NI-CA算法的优越性并没有过于突出，但对于其他三个网络NI-CA算法结果相较于其他算法更为准确，即NI-CA算法对各网络头部重点人评价适用性、准确性较高。该结果表明NI-CA算法整体上准确性较高，同时适用大型网络和小型网络。

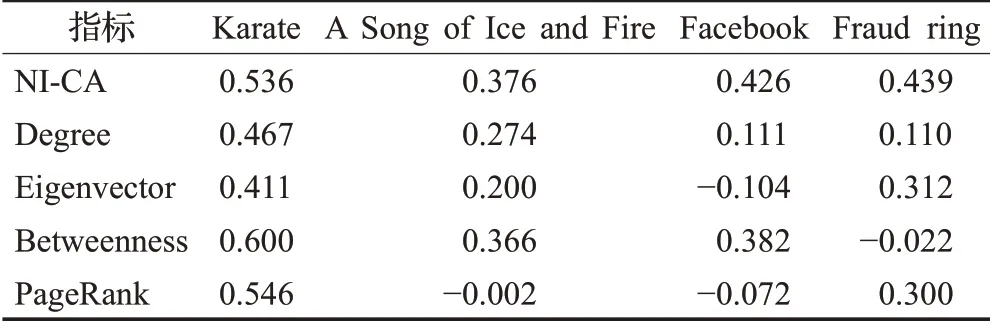
表2 肯德尔相关系数实验结果Table 2 Kendall correlation coefficient experimental results

4 总结

本文提出了基于社区评估的NI-CA算法，对划分社区后的目标人群进行社区评估分析，通过融合成员社区内部影响力和外部连通性，识别各社区的领袖人物，削弱传统节点重要性分析的“富人俱乐部”现象。于该理论，本文运用四个不同的社交网络进行验证，验证表明NI-CA算法准确性高，受网络结构特征的影响较小，所需数据维度少、普适性高，除用于目标人群关键人员挖掘，还可用于网络舆论控制等能抽象出具有此类网络拓扑特征的案件模型。

本文提出的方法还有一定的不足之处，本文在考虑节点的外部连通性上仍有改进空间。另外，在本文的研究基础上仍有需要进一步研究的事项，例如本文所使用的网络为静态网络，综合考虑网络中节点的时序特征对其重要性的影响。此外，有向网络和加权网络的重要节点挖掘，例如email交流的社交网络，考虑节点间关系的有向性和两节点之间的交流次数，也是后续工作的研究方向之一。