多目标优化特征选择研究综述

张梦婷，杜建强，罗计根，聂 斌，熊旺平，刘 明，赵书含

江西中医药大学 计算机学院，南昌 330004

近年来，许多研究者对特征选择进行了大量的研究。特征选择是指从已有的M个特征（feature）中选择N个特征(M＞N)，使得系统的特定指标最优化，是从原始特征中选择出一些最有效特征以降低数据集维度的过程，也是提高学习算法性能的一个重要手段。在机器学习[1]、图像处理[2]、数据挖掘[3]、生物信息学[4]和自然语言[5]等领域有着广泛的应用。特征选择要达到最大精度和最小特征子集两个目标，而单目标特征选择算法易融入主观偏好，从而影响特征选择的质量。因此多目标优化特征选择成为比较新且常见的方法之一，已经通过多种多目标技术和算法对特征选择进行了多项研究，亦成为众多机器学习、数据挖掘等领域的研究热点。

多目标优化（multi-objective optimization algorithms，MOA）的概念的初次出现是在1881年经济学领域，用于研究对平衡不同顾客要求的问题上。如今，多目标优化被应用在各个领域，如在工程领域[6]、工业污染[7]以及在焊接上[8]等；MOA的概念是在某个问题中在需要达到多个目标时，由于存在目标间的内在冲突，一个目标的优化可能会导致其他目标的劣化，因此很难出现唯一最优解，取而代之的是在他们中间做出协调和折衷处理，使总体的目标尽可能的达到最优。

在这个数据爆炸的时代，得到的数据来自各个领域，对凝炼特征质量的要求也越来越高。特征选择旨在去除冗余和无关特征，为达到最大精度的同时要求特征子集个数最小。为此，研究者将特征选择看作一个多目标优化问题，从最初使用基于先验的方法将多目标问题转换成单目标问题，到现在使用不同的进化算法来求解，取得了一些成果。李郅琴等人[9]对特征选择的方法进行综述，介绍了特征选择方法框架，描述了生成特征子集、评价准则两个过程，并根据特征选择和学习算法的不同结合方式对特征选择算法分类，但未涉及到多目标特征选择。Al-tashi等人[10]对多目标特征选择问题的挑战和问题进行系统的文献综述，并批判性地分析用于解决该问题的建议技术，但没有对多目标特征选择进行分类讨论。本文对多目标特征选择研究进行综述，将其方法进行分类讨论，并分析此研究当前存在的问题。

1 特征选择

特征选择（feature selection）是一个重要的数据预处理过程，常见的特征选择方法大致分为三种：过滤式（filter）[11]、嵌入式（embedding）[12]和包裹式（wrapper）[13]。过滤式是先用特征选择的过程对初始的特征进行筛选，然后用筛选后的特征进行模型的训练，并不会与学习器进行交互也不考虑特征与特征之间的关系。虽然过滤式的可扩展性好且速度快，但准确性并不高。嵌入式是将特征选择的过程与学习器的训练过程融为一体，在学习器的训练过程中，自动地进行了特征的选择，但只能在特定的模型中使用。包裹式的使用最为广泛，它的特征选择考虑到具体的学习器，是根据学习器上的误差来评价特征子集的优劣，在子集的搜索方式上使用了随机策略，考虑了特征与特征之间的关系，但是面对高维数据时计算量非常大。

特征选择是一个NP-hard[14]组合优化问题，假设一个n维数据集，可能存在2n的特征子集，仔细搜索这全部的特征子集显然是不可能的。如今，各种搜索方法已被应用于特征选择，如顺序向前选择（SFS）[15]、顺序向后选择（SBS）[15]等。然而这些方法存在局部搜索、计算量大以及嵌套效应等问题，而一些基于进化算法的元启发式搜索[16]可以提高搜索效率和解的质量，因此进化算法被广泛地应用于特征选择。

特征选择是许多分类和回归任务中常见的关键问题，特征选择有两个彼此冲突的目标：特征子集最小化和性能最大化。虽然子集个数增加会提高准确率，但子集的个数过多时可能会导致过度拟合以及泛化能力差等问题。特征选择方法倾向于使用最少数量的特征来提高算法（例如分类器）的学习性能，因此近年来使用多目标优化方法来解决特征选择的情况显著增长。与单目标优化方法相比，借助多目标优化方法在特征选择上可以更有效地探索搜索空间，并找出质量更高的特征子集。

单目标特征选择，即采用单一的指标（如模型的精度或特征子集的个数）对特征子集进行评估，这种方法常专注于某一指标而忽略另一个。在实际研究中，模型预测的精准度和特征子集的数目都是特征选择中的主要问题。因此，许多研究者试图同时解决特征选择的多个问题，并采用多目标优化的方法来解决特征选择问题，称为多目标特征选择。

2 多目标优化

基于元启发式搜索的特征选择问题可以根据目标的数量将优化问题分为两类：单目标和多目标优化。单目标优化的情况下，只有一个目标，任何两个解都可以依据单一目标来比较其好坏，最后得出无可争议的最优解。而多目标优化与传统的单目标优化相对，多目标优化问题要解决的是使给定的多个目标函数尽可能同时达到最佳，不存在唯一的全局最优解。多目标优化的解通常是一组均衡解，即一组由众多Pareto最优解[17]组成的集合，其中Pareto解又称非支配解或不受支配解，在有多个目标时，由于目标之间的冲突和无法比较的现象，在改进任何目标函数的同时，必然会削弱至少一个其他目标函数的解称为Pareto解。

2.1 多目标优化的方法

多目标优化需要同时优化两个或者两个以上的目标函数，且各目标函数之间相互冲突，不能显式地平衡它们，即一个目标的优化可能引起另一个目标的衰落，不能使每个目标函数达到最优。多目标优化的方法主要分为基于先验[18]和基于后验的方法[19]。在解决多目标的实际问题时，特征选择将被视为最大化或最小化问题。如果目标数量为n，则一个标准的多目标优化数学模型应该表示见公式（1）所示。多目标优化方法旨在获取一组非支配最优解或特征子集。

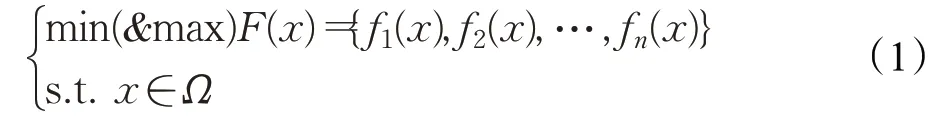
2.1.1 基于先验的方法

基于先验的方法又称传统优化算法，包括加权法[20]、约束法[21]和最小最大法[22]等方法。传统的多目标优化算法是通过分析、分解和替换将多目标问题转为单目标问题再用单目标优化技术进行求解，因而每次只能得到Pareto解集中的一个。

（1）加权法

加权法就是对多目标优化问题中的N个目标按其重要程度赋以适当的权系数，其乘积和作为新的目标函数，再求最优解。使用加权求和法求解特征选择问题，如加权求和法可以将多目标优化表示为：

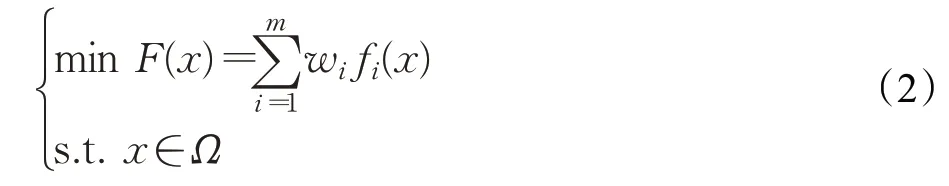
（2）约束法

在1971年约束法被提出，其原理是将某个目标函数作为优化目标，而约束其他目标函数的方法来求解多目标优化问题。多目标优化中的约束法的数学模型可表示为：

为了得到不同的Pareto最优解，εi作为上界可以取不同的值，Xf则为解的集合。

（3）最大最小法

起源于博弈论的最小最大法是为了求解多目标问题而设计的，其原理是通过最小化各个目标函数值与预设目标值之间的最大偏移量来寻求问题的最优解。其数学模型可以表示为：

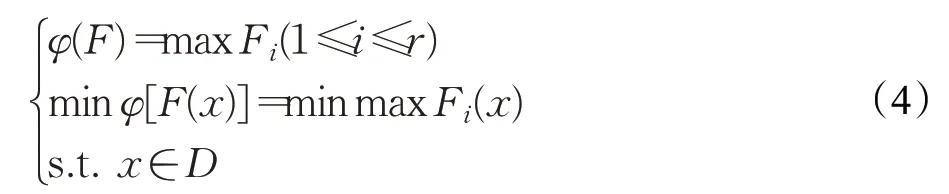
基于先验的方法的优势在于可以利用已有且成熟的单目标优化技术来求解，有计算量小、速度快、有充分理论支撑等优点，使其更适合于实际应用，但其要求决策者在不知道任何替代方案之前明确且准确地权衡不同的目标，导致该方式存在一些缺陷，如多个目标函数的单位不统一；分配的权值是否存在主观性等。

2.1.2 基于后验的方法

受自然界生物系统的启发，智能优化法已成为多目标优化领域的一个热门话题。它以其全局搜索能力而闻名，因此广泛应用于特征选择。而大多数的智能优化算法是基于后验的方法来实现的，关键点是它们在优化过程的每次迭代中操纵一组解决方案。换句话说，可以在一次运行中产生多个权衡解决方案，这使它们能够在多目标优化中显示出良好的效果。智能优化算法克服了线性加权等传统方法受权值影响的缺点，有着快速的全局搜索能力且不依赖于先验知识。

自Schaffer[23]首次将进化算法用于解决多目标优化问题后，很多研究者不断提出新的多目标进化算法，目前已有遗传算法（GA）[24]、粒子群算法（PSO）[25]、蚁群算法（ACO）[26]等一系列智能优化算法用来解决多目标优化问题。近年来，使用智能优化算法解决特征选择问题的文献显著增多。基于后验的多目标优化方法也已被应用于处理现实世界的问题，例如颜景斌等人[27]采用基于NSGA-II算法的多目标优化方法来解决SWISS整流器的性能问题；李琳等人[28]根据动态变化的外部环境调整面向服务软件的部署方案，对传统多目标蚁群算法进行改进，引入摒弃精英解策略以避免算法早熟收敛，提出一种求解面向服务软件部署优化问题的多目标蚁群算法。

基于后验的方法通过进化算法的代与代之间维持由潜在解组成的种群来实现全局搜索，从而解决多目标优化问题，是一类模拟生物进化机制而形成的全局性概率优化搜索方法。但当目标是高维时，非支配个体在种群所占的比例随着目标个数的增多而上升，部分个体变成非支配解，从而大大削弱了基于Pareto支配进行排序与选择的效果，导致进化算法搜索能力下降。

2.2 多目标优化的评价准则

多目标优化问题的评价标准不同于单目标，单目标的评价直接取决于最终解的好坏，而想要验证一个多目标优化算法的好坏往往取决于一个解集的质量。多目标优化算法主要有两个评价标准：收敛性、多样性，多样性又包括解集分布的均匀性和广泛性。多目标优化解集方案的性能评估一直也是研究的热点，最新文献表明现如今有70多种性能指标[29]，其最常用的性能指标有世代距离（GD）、最大分散度（MS）、SP、逆世代距离（IGD）、ε指标和超体积度量（HV）。其中，后三个性能指标能综合考虑两个评价标准。

（1）世代距离（generational distance，GD）

Veldhuizen和Lamont[30]在1999年提出了GD指标，它表示求出的最优边界PFknown和真正的最优边界PFture之间的间隔距离，该距离表示偏离真正边界的程度。GD的值越大，偏离真正的最远边界越远程度越高，收敛性就越差。GD的公式表示为：

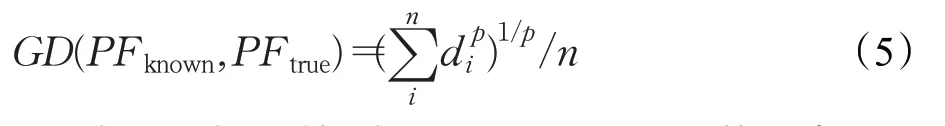
其中，p表示目标维数，当p=2时为欧几里德距离。n表示PFknown中点的个数。di表示目标空间上第i个解与PFture上相距最近的参考点之间的欧式距离。

（2）最大分散度（maximum spread，MS）

MS[31]是一个广泛使用的分布性指标，用于衡量所得PFknown对PFture的覆盖程度，它通过考虑每个目标的最大范围来衡量解决方案的范围。其中，aj和a′j表示两个不同的目标，m为目标的个数，当m=2时，非支配解集的MS值是其两个极值解的欧氏距离。它没有考虑集合的收敛性，远离帕累托前沿的解通常对MS值有很大贡献，因此很多研究者对其进行了相应的改进。MS的数学公式表示为：

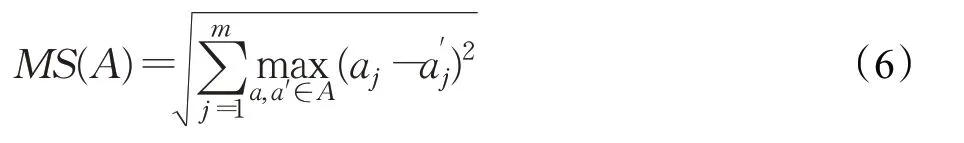
（3）SP（spacing metric）

SP是Schott[32]提出的性能指标，度量每个解到其他解的最小距离的标准差，是最受欢迎的分布性指标。SP值越小，说明解集分布的越均匀。但SP仅度量解集的均匀性，没有考虑它的广泛性。

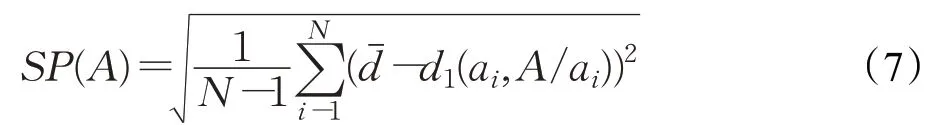
其中，A=a1,a2,…,aN，dˉ是所有d1平均值，即ai与集合A/ai的L1范数距离。

（4）逆世代距离（inverted generational distance，IGD）

逆世代距离（IGD）[33]是世代距离的逆向映射，它表示问题真正的最优边界PFture到算法所求得的非支配解集PFknown的平均距离，如图1所示，IGD计算的是图中Reference Solutions到最近的Solutions的平均距离，即Pareto近似前沿上的每个参考点到解集中最近的解的平均距离。

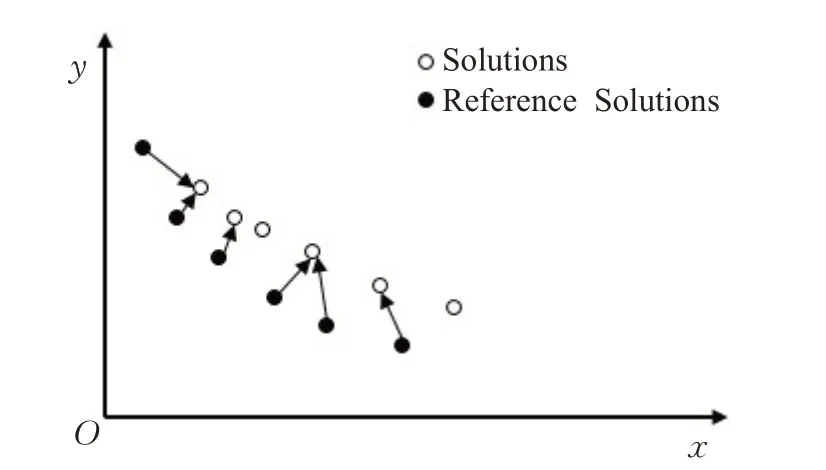
图1 IGD指标Fig.1 Inverted generational distance indicator

IGD的值越小，获得的解集越好，它不仅能反应解集的收敛性，还能反应解集的均匀性和广泛性。IGD的公式表示为：

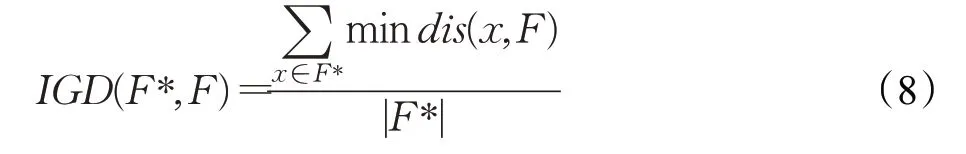
其中，F*是PFture上均匀选取一定数目的个体，F为算法求得的最优解集。mindis(x,F)表示F中的个体到个体x之间的最小欧几里德距离。

（5）ε指标

ε指标是Zitzler等人[34]在2003年提出的，考虑了解集之间的最大差异，它给出了一个因子，在考虑所有目标的情况下，一个近似集比另一个更差。形式上，设A和B为两个近似集，则ε(A,B)等于最小因子，使得对于B中的任何解，A中至少有一个解不会因考虑所有目标的因素而变差。ε指标有两个版本加法ε+指标和乘法ε×指标，数学公式表示如下。两个版本都是指标值越小越好，当ε+(A,B)≤0或ε×(A,B)≤1时意味着A弱支配B。

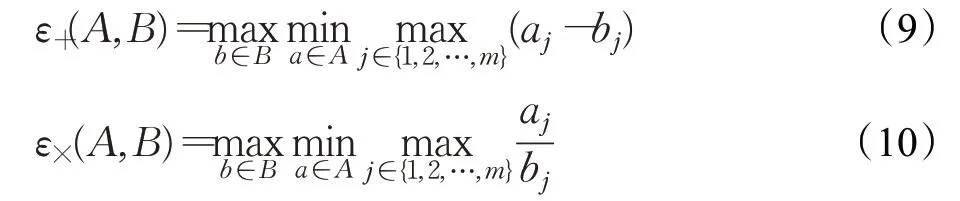
其中，m为目标的个数，a和b分别是A和B中的解，aj表示a的第j个目标。

（6）超体积度量（hypervolume，HV）

HV性能指标最早是由Zitzler等人[35]提出的，如图2所示，它表示由解集中的个体（图中Solutions）与参考点（图中的Reference Solutions）在目标空间中所围成的超立方体的体积（图中的阴影部分）。HV是当前评价多目标优化算法中可信度最高的指标，能同时衡量算法的收敛性和多样性，但受参考点的影响比较大。它的评价方式与Pareto一致，如果一个解集S优于另一个解集S1，那么解集S的HV指标也会大于解集S1的。

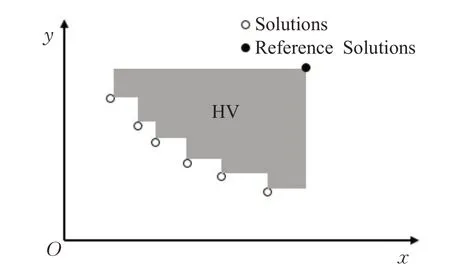
图2 HV指标Fig.2 Hypervolume indicator

3 多目标优化特征选择

多目标问题具有多个目标函数，现实世界大多数的问题本质上都是多目标问题，特征选择问题也被认为是其中之一。将特征选择作为一项多目标任务进行研究，在这种情况下，选择特征的准确性和数量的目标函数一起演变，这允许同时评估不同维度的特征集。多目标特征选择的方法可以消除在处理基于适应度的探索和利用阶段时观察到的陷阱，在特征数量和性能两个目标之间取得最佳平衡。

研究者起初使用传统的优化方式将两个目标合并成一个目标进行特征选择，如Chuang等人[36]使用加权求和法将特征数量和分类精度两个目标合并为一个目标求解；Tran等人[37]将分类精度和距离两个目标一起考虑。随后，研究者试图同时优化特征选择的两个目标，将基于进化计算的特征选择算法引入多目标优化，如Got等人[38]提出了一种使用鲸鱼优化算法（WOA）的新型混合过滤器包装的多目标特征选择方法；Wang等人[39]研究了一种基于样本缩减策略和进化算法的多目标特征选择框架，将基于粒子更新模型的改进人工蜂群算法嵌入到框架中，提出了一种快速多目标进化特征选择算法。根据特征选择的评估措施不同，将多目标特征选择分为基于过滤式的、基于包裹式的和基于混合式的三类。

3.1 基于过滤式的多目标特征选择

基于过滤式的方法是使用信息理论准则来评估一组特征的优度，通过性能度量选择特征，再使用学习器进行训练，所以基于过滤式的方法不依赖于学习器。过滤式的评价准则包括：信息度量、距离度量、依赖性度量以及一致性度量（只适用于分类）等。其中，信息度量和依赖性度量使用最为广泛。基于过滤式的多目标特征选择通常需要优化的矛盾目标为相关性、冗余和特征子集大小。下面对近些年基于过滤式的多目标特征选择的研究进行综述，过滤式中各种方法的对比见表1。

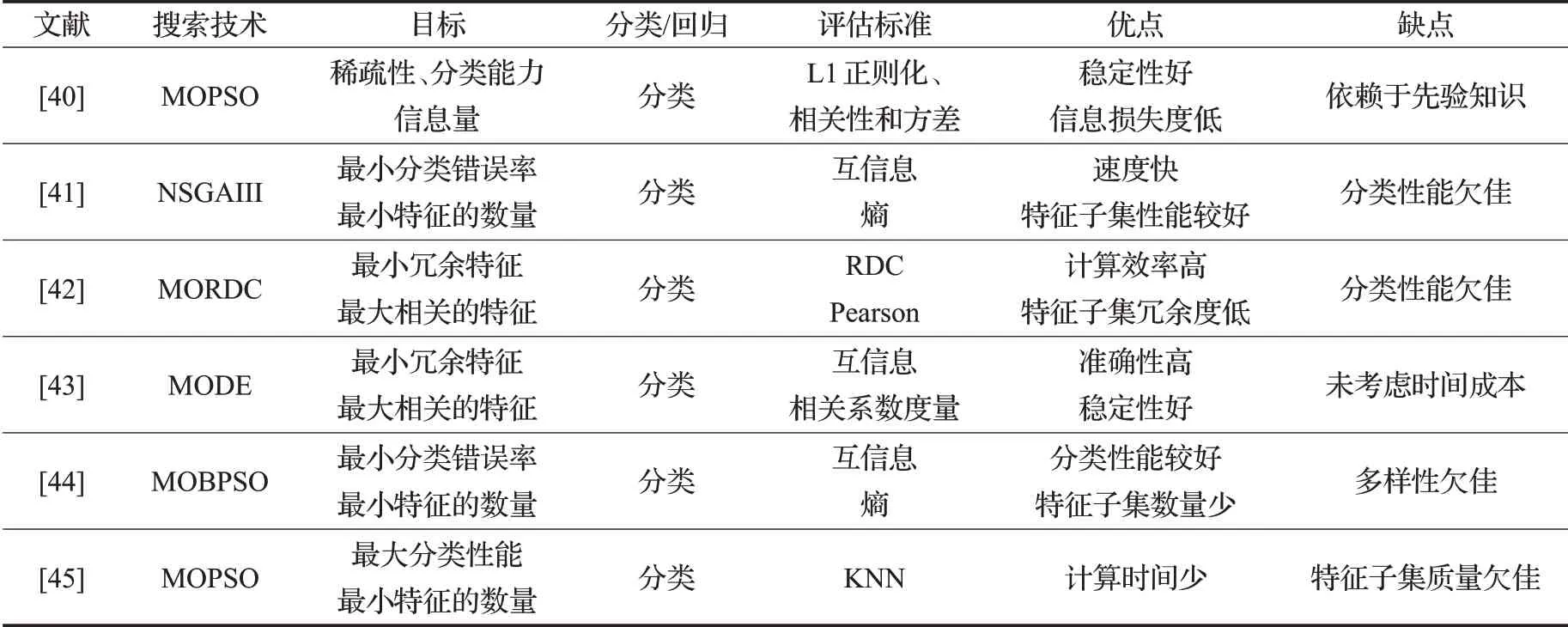
表1 基于过滤式多目标特征选择Table 1 Filter based multi-objective feature selection

文献[40]综合考虑特征子集的稀疏性、分类能力和信息量等多个目标函数，提出一种基于子集评价多目标优化的特征选择框架，使用多目标粒子群算法（MOPSO）进行特征权值向量寻优，实现基于权值向量排序的特征选择，将特征子集的信息量作为评价函数之一，使得该方法有较好的稳定性且信息损失度低；文献[41]采用互信息和基于增益比的熵作为滤波器评价指标，使用二元杜鹃优化算法与非支配排序遗传算法NSGAIII和NSGAII相结合，提出了两种不同的基于多目标滤波器的特征选择框架，来寻找具有最小错误率的更少特征，使用成对评估来衡量两个特征之间的关系，不涉及相关性和冗余的复杂计算，故速度快且特征子集性能较好，过滤器更快扩展到大型数据集但缺乏良好的分类性能。文献[42]提出了多目标相对判别准则（MORDC）的方法来平衡最小冗余特征和与目标类最大相关的特征使特征子集冗余度低，并采用多目标进化框架来搜索解决方案空间，计算效率快。文献[43]提出了一种基于精英主义的多目标差分进化特征选择算法（FAEMODE）的过滤方法，考虑了特征之间的线性和非线性依赖，以处理数据集的冗余和无关特征，这导致选择一个特征子集，该子集对数据集的良好和稳定分类具有很高的潜力且预测准确性高，但未考虑时间成本。文献[44]基于非支配排序和拥挤距离思想以及二元粒子群（BPSO）开发了两种新颖的多目标分类特征选择框架，应用互信息和熵作为两个不同的过滤器评估标准，得到一组使用较少特征的解，熵作为评价标准可以发现一组特征之间的多向相关性和冗余性，从而进一步提高分类性能且使用更少的特征，但由于更新机制失去了群的多样性。文献[45]首次对多目标粒子群算法（PSO）进行特征选择的研究，考虑了两种基于PSO的多目标特征选择算法，即NSPSOFS和CMDPSOFS。前者将非支配排序的思想引入到PSO中，以解决特征选择问题。后者将拥挤、突变和优势的思想应用于PSO，以搜索Pareto前沿解，CMDPSOFS采用不同的机制来维持领导者和群体的多样性，使计算时间更少，但在NSPSOFS中快速丢失群多样性的潜在局限性限制了其特征选择的性能，故特征子集质量欠佳。

基于过滤式的方法独立于学习算法，使用数据的统计特征进行评估。与基于包裹式方法相比计算成本更低，有效地消除无关和嘈杂的特征，但忽略了特征组合的影响。

3.2 基于包裹式的多目标特征选择

基于包裹式的多目标特征选择与基于过滤式的不同，前者会通过一些优化算法来考虑特征之间的关系，需要用学习器来评估特征子集的优劣。基于包裹式的方法中用以评价特征的学习算法是多种多样的，例如决策树、神经网络、贝叶斯分类器、近邻法以及支持向量机等。其通常优化的目标为最大化精度，同时最小化特征子集大小。目前，已经有许多研究者使用包裹式来做多目标特征选择且取得了一些成果，本文对近几年的基于包裹式的多目标特征选择文献进行综述，具体方法之间的对比见表2。

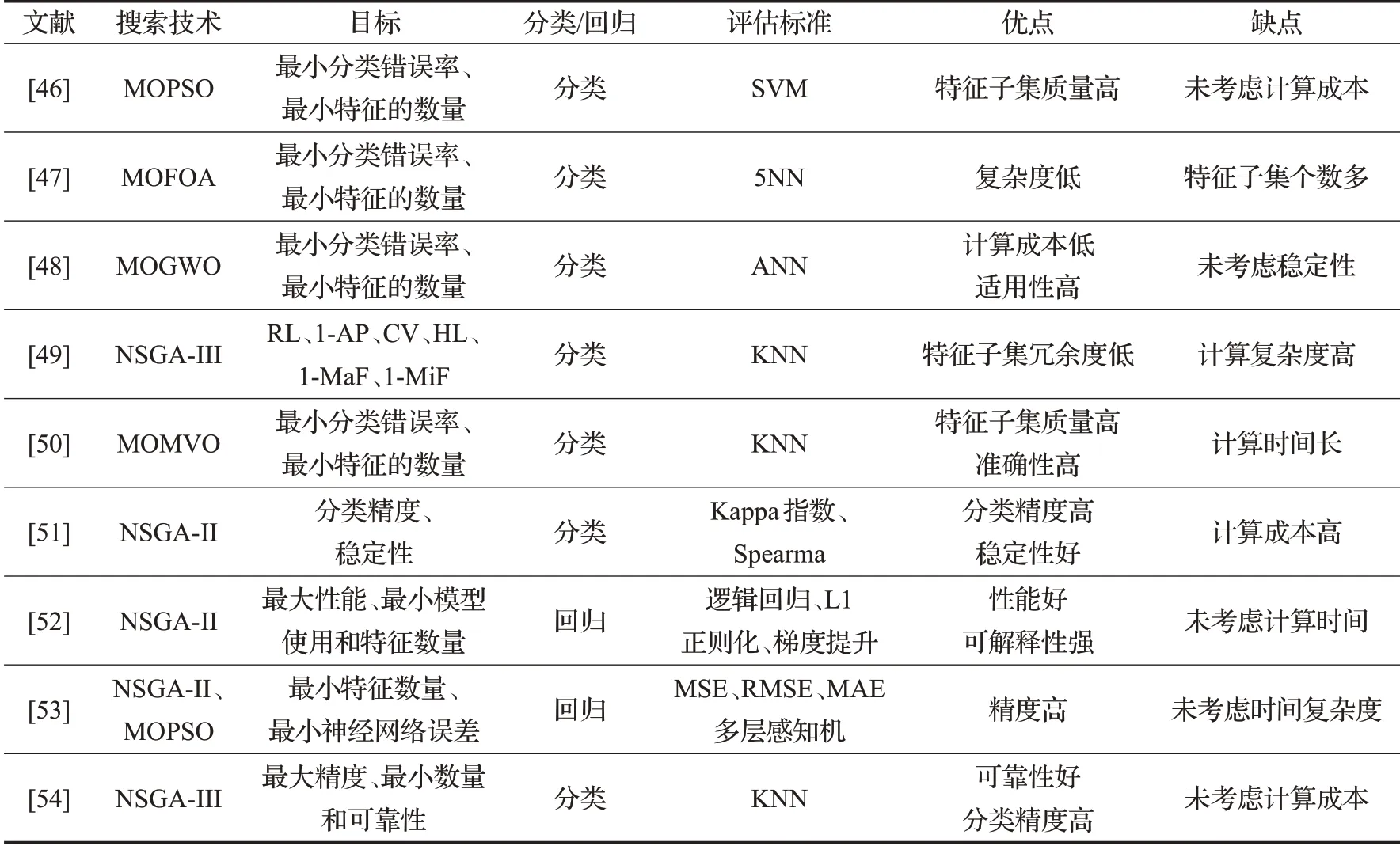
表2 基于包裹式多目标特征选择Table 2 Wrapper based multi-objective feature selection

文献[46]提出一种改进的基于拥挤、变异和支配策略的多目标粒子群特征选择（CMDPSOFS-II），引入了差分进化的变异和选择方式，解决了之前均匀变异带来的收敛速度慢的问题，更好地平衡了全局和局部搜索能力，在特征数相等时，CMDPSOFS-Ⅱ可以选出错误率更低的特征组合，特征子集的质量高，但未考虑计算成本。文献[47]提出了一种基于森林优化算法（FOA）的多目标特征选择算法，使用了存档、网格和基于区域的选择概念，通过选择较少的特征数量，在大多数情况下能够减少分类错误，使用简单的算子来产生新的解并用存档来保存非支配解，故花费更少的计算时间，与高维数据集中的其他多目标方法相比，该算法无法选择较少数量的特征。由于最初的多目标灰狼优化器（MOGWO）不能直接用于解决本质上是离散的多目标特征选择问题，文献[48]提出了基于sigmoid传递函数的MOGWO的二进制版，且通过包裹式的人工神经网络（ANN）来评估选定特征子集的分类性能，该算法参数较少，这对于大型数据集在时间消耗方面更有帮助，且适用于各类数据集，适用性高，但未考虑稳定性。文献[49]提出了一种基于多目标优化的多标签特征选择算法（MMFS），通过改进具有两个档案的NSGAIII算法来提高它的多样性和收敛性。该方法可以平衡多个目标，去除不相关和冗余特征且获得满意的分类结果，由于使用包裹式，计算成本较大。文献[50]提出了多节优化器（MVO）的二元多目标变体（MOMVO）来处理特征选择任务。该方法基于三个宇宙学概念：白洞、黑洞和虫洞。此外，针对标准MOMVO存在局部最优停滞的问题，还提出了MOMVO的一种变体，该变体在更新中纳入了个人最佳解决方案。与大多数进化的包裹式方法不同，所提出的基于MOMVO的方法将模型的准确性和维数的减少作为多目标优化问题，由于传统MOMVO的探索性和开发性优势，提高了分类精度，包裹式在选择相关子集时可以使用标签或依赖项，进而提高特征子集的质量，但计算时间长。文献[51]为了避免包裹式方法通常会遇到的过度拟合问题，提出了一种基于多目标进化算法的特征选择包裹式方法，精心设计了该方法中个体或潜在解的表示以及育种算子和目标函数，以选择小部分具有良好泛化能力的特征，两个目标函数旨在避免对群体中的每个个体应用交叉验证评估，这将需要更多的计算时间，为了分析所提出的包装方法的稳定性，还提出了一种新的特征排序。文献[52]介绍了一种用于信用评分中特征选择的多目标利润驱动框架，将预期最大利润（EMP）和特征数量似为两个适应度函数，以解决盈利能力和可理解性问题。使用遗传算法NSGA-II执行多目标优化，提出的方法比传统特征选择策略更少的特征产生更高的预期利润，但未考虑计算时间。文献[53]提出了基于NSGA-II和MOPSO的两种新方法来预测华法林剂量。与经典方法相比，多目标优化方法具有更高的准确性，且通过实验对比，使用多目标粒子群算法（MOPSO）有更高的精度和准确性，但未考虑时间复杂度。文献[54]针对分类问题中缺失数据的问题，将可靠性作为特征选择的第三个目标，提出了非支配排序遗传算法III（NSGA-III）并采用平均插补法来处理缺失数据，有很好的可靠性。NSGA-III将个体与每个参考点相关联，并有效地选择了与参考点相关性较小的个体，故有更好的性能，其与四种流行的多目标优化算法相比，在IGD和HV方面都优于其他方法，但未考虑计算成本。

基于包裹式的方法相对于过滤式的方法来说，找到的特征子集更优，但选出的特征通用性不强，且计算复杂度很高，特别是面对高维数据时需要更大的成本代价，算法的执行时间很长。

3.3 基于混合式的多目标特征选择

结合过滤式和包裹式的优点提出了混合式特征选择方法，其应用过滤式技术来减少特征空间，再使用包裹式方法进行最终的特征选择。如今，基于混合式的多目标特征选择的应用不断增多，尤其是在处理一些高维数据，同时利用过滤式的速度和包裹式的精度能有效实现高质量的特征子集。下面对基于混合式的多目标特征选择的最新文献进行综述，具体对比见表3。

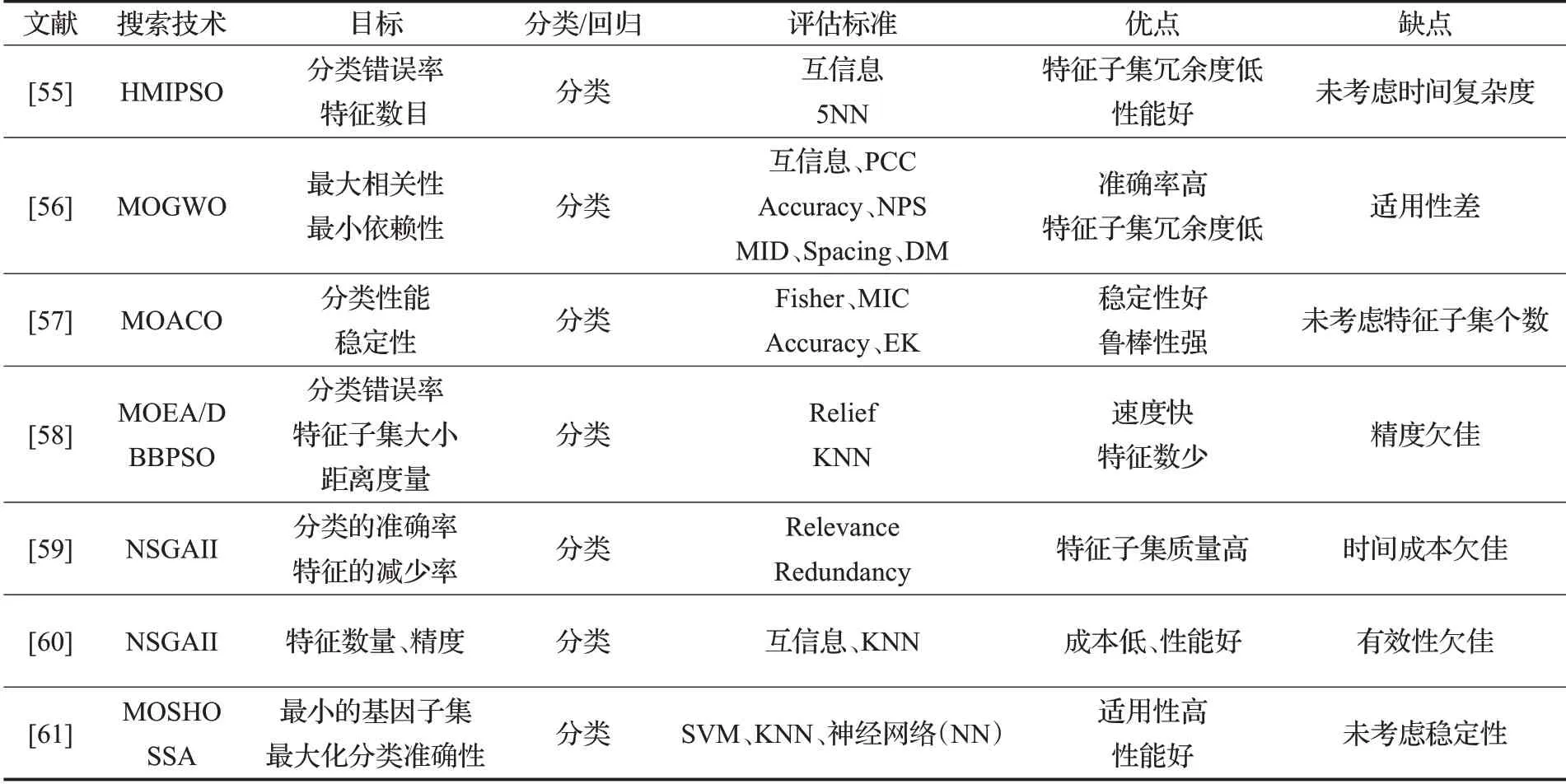
表3 基于混合式多目标特征选择Table 3 Hybrid based multi-objective feature selection

文献[55]利用自适应突变操作来扰动种群，避免粒子群算法陷入局部最优的问题，以及利用互信息来表示数据间的依赖程度，提出了混合互信息和粒子群算法的多目标特征选择的方法（HMIPSO），因此能够很好地降低特征个数以及分类错误率。结合互信息和新的集合知识提出了一种局部搜索策略，删除了不相关和冗余特征，筛选出的特征子集冗余度低，但未考虑时间复杂度问题；文献[56]结合互信息和皮尔逊相关系数两种评价准则提出一种慢性肾病预测的多目标特征选择模型。在GWO的基础上采用精英反向学习、非线性控制参数和联想记忆策略三个改进算子来提高对慢性肾病的预测准确率，考虑了最大化特征数与类别之间的相关性以及最小化特征之间的依赖性使特征子集冗余度低，但该模型不适用于其他医学临床数据。文献[57]针对进化算法特征选择稳定性问题，提出一种面向稳定特征选择的多目标蚁群优化方法。采用信息增益、卡方检验和ReliefF三种特征排序法作为多目标蚁群优化的稳定性指导信息，聚合特征的费舍尔分值和最大信息系数值启发式信息，很好地平衡了分类性能和稳定性能，且稳定性变化趋势较为稳定有着很好的鲁棒性，但该方法未考虑筛选出特征子集的个数。文献[58]对于高维数据的特征选择问题，提出一种基于两级粒子协作的特征选择多目标优化。同时考虑特征数量、分类错误率和距离度量三个目标，使用二进制粒子群优化两级粒子合作策略，有效地减少特征数量，将随机生成的普通粒子和经过ReliefF过滤的粒子组合，保持快速收敛，加快了速度，虽然实现具有竞争力的分类精度，但NSGA-COPSO在平均分类精度方面略优于MOEA/D-COPSO。文献[59]充分利用filter法和wrapper法的优点，提出了一种交互式过滤式-包裹式多目标进化算法。该方法采用引导和修复策略来选择高质量的特征子集，准确性和所选特征数量方面优于现有的现有技术，随着实例数量的增加，算法中包裹式评估时间变得更长，这导致GR-MOEA的总运行时间变长，时间成本欠佳。文献[60]提出了一种结合遗传算法和局部搜索进行特征选择的多目标混合方法。优化两个过滤式目标，即特征数量和互信息，以及一个与精度相对应的包裹式目标，以降低特征的维数并提高分类性能，平衡了全局和局部搜索获得更好的性能，将过滤式和包裹式结合，保持分类性能并降低成本，但只考虑了epsilon指标，没有使用其他质量指标，故有效性欠佳。文献[61]为了实现最小的基因子集和最大化分类准确性两个目标，提出了使用多目标斑点鬣狗优化器（MOSHO）和萨尔普群算法（SSA）进行基因选择的框架（C-HMOSHSSA），利用SSA和MOSHO的特性来促进其探索和利用能力，有较好的性能，在四个分类器上训练后，结果显示所提出的技术成功地识别了新的信息和生物相关基因集，且可以应用于特征选择其他的问题领域，适用性高，稳定性也是特征选择的一大难题，但该方法未考虑稳定性。

4 总结与展望

本文阐述了多目标优化的方法和评价准则和特征选择的本质，然后详细分析了多目标优化特征选择的方法和区别。将特征选择问题描述为多目标优化问题有助于获得一组最优特征子集，以满足决策者的各种需求。尽管各种多目标特征选择的方法被提出，但仍然存在一些问题需要深入研究。

（1）在多目标优化特征选择中，基本是使用特征子集的个数和性能两个目标。而在做特征选择时往往有多个评价指标如稳定性、复杂性等，且这些评价指标会影响最终解的选择。因此，将多个评价指标同时作为优化目标也具有一定的挑战性。

（2）当优化目标增多时，会一定程度上带来决策选择和复杂度等问题。因此，当优化目标增多时如何解决其带来的问题也有待研究。

（3）对于高维特征选择问题，Pareto最优解通常是稀疏的，大多数决策变量为零。而使用大多数现有的多目标进化算法解决此类问题是困难的。

（4）分类和回归问题是机器学习的主要问题。目前大多数多目标优化特征选择都用于分类，很少用于回归问题中，而现实问题中回归依然很重要。因此，多目标特征选择的回归问题很值得研究。

（5）从进化算法的角度来讲，目前已有遗传算法（GA）、粒子群算法（PSO）、蚁群算法（ACO）等一系列算法用来解决多目标优化问题，但用的比较多的还是遗传算法和粒子群算法。随着一些新兴的进化算法的出现，未来还有更多的算法值得挖掘并应用在多目标特征选择上。