考虑渗流影响的水热型地热田地温预测

张通，张延军，白林

(吉林大学建设工程学院，吉林 长春 130026)

0 引言

地热能清洁可再生，相对于传统能源有明显的环保优势，其平均利用系数达到0.73，若能有效开发，将在很大程度上解决我国现阶段存在的能源难题[1]. 水热型地热资源一般以热水的形式埋藏在200～3 000 m深度的地下，或直接以热泉等形式出露于地表. 准确获取地下温度场信息是安全开发地热能的关键环节. 传统地热钻井由于成本原因，获取的地温数据有限. 因此，结合模型方法对地热异常区地温分布进行预测成为研究热点. 足量的原位数据是模型预测性能的保证，相对于少量的钻孔测温数据，浅层测温法通过快速测量1～5 m深度地温数据，可以辨别数百米深度热源在浅层产生的热异常[2]，对模型表层温度边界的确定和数据的扩充具有实际帮助. 早期这项技术主要应用于已知地热区域的进一步筛选. 近年来，Coolbaugh等[3-4]利用浅层测温法在美国内华达州地热隐伏区成功探测出7处地热田. 浅层测温结果对于中低温水热型地热系统热异常范围、 分布面积和地下热水流场的圈定方面发挥很大作用[5].

受降雨、 日照等环境因素影响，直接以浅层地温数据圈定热异常范围通常会有偏差，而结合基于传热学理论的地温预测方法预测更深层地温，以此获取地热异常信息，其可信度更强. 现有研究中，主要将地温场分为传导型和传导-对流型. 万志军等[6]通过三维稳态热传导理论建立地温反演方法，预测高温岩体地热资源量； 张永亮等[7]通过建立考虑地形校正的地温场深部温度推算模型，预测矿山深部地温； 张延军等[8-9]、 张庆等[10]采用基于浅层测温数据和一维稳态热传导理论的地温预测模型，对厦门东山热田、 安庆迎江区地温场进行预测. 在地下水活动区域，渗流对地温场的影响不可忽视. 鉴于地温场中热渗耦合过程复杂，数值模拟方法常被用来解决此类问题. 陈金龙等[11]通过建立考虑地下水流动情况下的多裂隙岩体-渗流数学模型，分析水力梯度变化对涿鹿盆地内部温度场的影响规律； 吴志伟等[12]基于Lu模型，研究考虑参数非均质性的饱和-非饱和渗流场与浅部温度场的耦合问题； 张文兵等[13]引入土体有效热导率，通过构建考虑非均质传热的水热耦合模型，模拟河岸带温度场分布. 在这些研究中，渗流影响因素的选择和渗流层土体热物性参数的表征是研究关键.

本研究依托浅层地温、 岩土热物性、 地下水位等数据，建立基于一维稳态热传导的地温预测模型. 模型考虑渗流的影响，以渗流速度v、 渗流层厚度h、 地下水与流经区域的温差Δt作为影响因子，应用TOUGH2软件建立水热耦合数值模型，分析渗流对地温预测结果的影响规律，建立渗流层等效热导率λe与各影响因子的回归关系. 选择厦门后埔地热田作为模型验证场地，实地开展浅层测温试验后，对研究区20 m深度地温进行预测，以实测地温验证模型预测地温的准确性.

1 研究区概况

后埔地热田位于厦门市同安区莲花镇后埔村，属低山丘陵地貌单元，面积约0.81 km2. 区域内存在断裂F1、 断裂F2和断裂F3，如图1所示. 其中，F1和F2为后埔-东塘断裂带在区域内的主要表现，走向北西西275°～295°，倾角大于75°，向北东倾斜； F3为长乐-南澳断裂带的次生断裂，走向北北东10°～30°，倾角大于80°，向南东倾斜. 区域内侵入岩主要为燕山早期花岗闪长岩、 似斑状含黑云母花岗岩和细粒花岗岩，这些岩层受两条断裂切割，为地热资源提供良好的赋存空间，上部的第四系冲洪积层则形成热储盖层. 区域内地下热水受断裂构造控制呈脉状，分布于莲花溪北侧的一级阶地和河漫滩中，并形成地热异常，在区内没有发现温泉出露点.

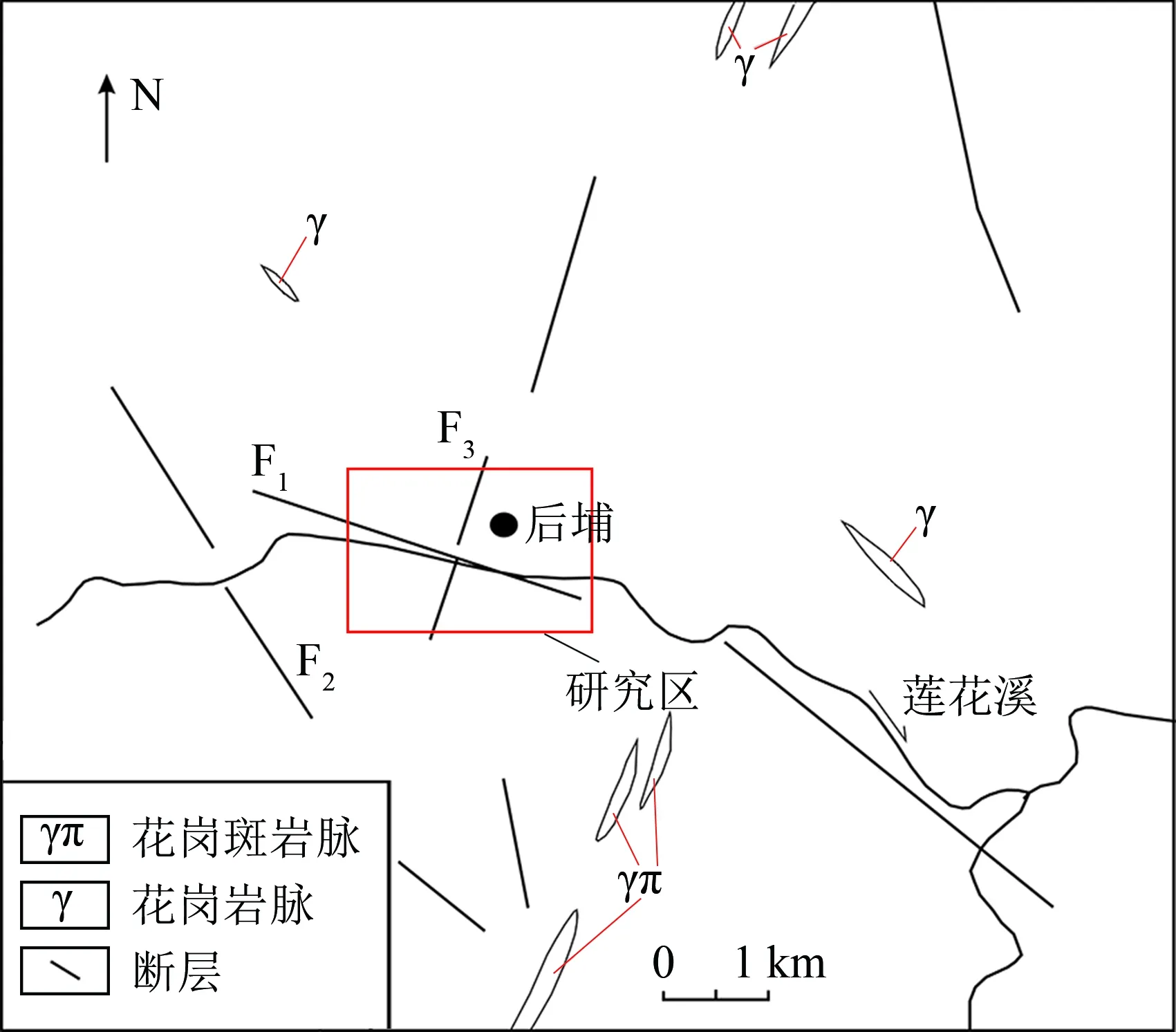
图1 研究区位置和地质略图

厦门地质工程勘察院曾对后埔地热田地下热水资源进行过调查，以获取20 m深度地温信息. 结果显示，后埔地热田为中低温水热型地热资源，地热异常区形态呈不规则长椭圆状，长轴走向近南北，包含两个地温异常中心点，其20 m深度地温分别为44.8和44.9 ℃[14].

2 地温预测模型

2.1 模型基本原理

地表1 m深度以下，24 h太阳辐射循环造成的地温变化有限，短期内可将其假设为稳态温度场. 对地球内热向浅层的传递作如下简化：

1) 不考虑热辐射和热对流，地层中只存在热传导1种导热形式；

2) 在热量传递过程中，热流密度和地层热物性参数保持不变；

3) 热量沿垂直方向传递，为一维稳态热传导.

由导热微分方程和第一类边界条件可以求解地层中的温度分布：

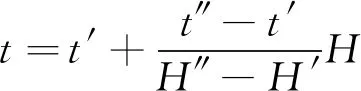
(1)

由傅里叶定律可以求得浅层热流密度：

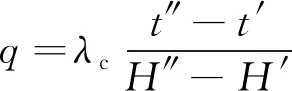
(2)

预测深度地温的计算公式为：

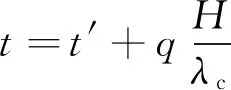
(3)

式(1) ～ (3)中：t、t′、t″分别为预测地温和两个已知地温，单位为℃；H为预测地温深度至已知地温t′深度的距离，单位为m；H′、H″为两个已知地温的深度，单位为m；q为浅层热流密度，单位为W·m-2；λc为H范围内的地层综合热导率，单位为W·(m·K)-1.

式(3)为一维稳态热传导模型的理想公式. 实际地层间传热复杂，尤其在渗流区域. 当地下水与流经区域间存在温差时，会产生热补给或热损失，在这些区域进行地温预测若不考虑渗流的影响，将会产生较大误差，因此需要对上述理想公式进行修正.

2.2 水热耦合模型

为综合分析不同渗流参数对地温预测的影响，并对预测模型进行修正，参考后埔地热田拟预测深度和地层参数，采用TOUGH2软件建立水热耦合数值模型. TOUGH2是一款多相多组分的水热耦合模拟程序，常被用来计算地热领域的水热耦合. 本研究选用其中的EOS1模块，该模块可模拟水或者具有示踪性质的水的运移.

恒温层是太阳辐射热向地表下释减与地球内热向地表传导释热达到平衡的地层层位，恒温层以下的地温分布更适宜确定热异常范围. 福建省南部恒温带的顶板埋深多在10～15 m之间[15]. 考虑20 m深度已有实测地温资料，且位于恒温层之下，因此将其作为建立数值模型和地温预测的目标深度. 模型的长、 宽、 深分别设为200、 200、 20 m，总网格数为20 800个，自上而下概化为5层. 第1层土质为粘土，温度设置为厦门市年平均气温22 ℃，模拟地表温度边界； 第2、 4层为隔水层，土质为粘土； 第3层为渗流层，土质为细砂； 第5层土质为粘土，温度设置为50 ℃，模拟固定温度边界.h为2 m时的地层参数(底板埋深、 土质、 密度ρ、 热导率λ、 比热容c、 孔隙比e和渗透系数k, 见表1)，其余工况地层物理参数与其相同，仅渗流层顶底板深度不同.

表1 模型地层参数

设置地下水在整个渗流层沿x轴方向流入流出，不发生跨层渗流，但可在渗流层内自由流动.以h、v、 Δt作为地温预测模型的渗流影响因子. 其中，h取2、 4、 6、 8 m，v取50、 100、 150、 200、 250、 300、 350、 400 m·a-1，Δt取0、 2、 4、 6、 8、 10 ℃，地下水温度不大于流经区域温度，即渗流会产生热损失. 水热耦合模型初始状态如图2所示.

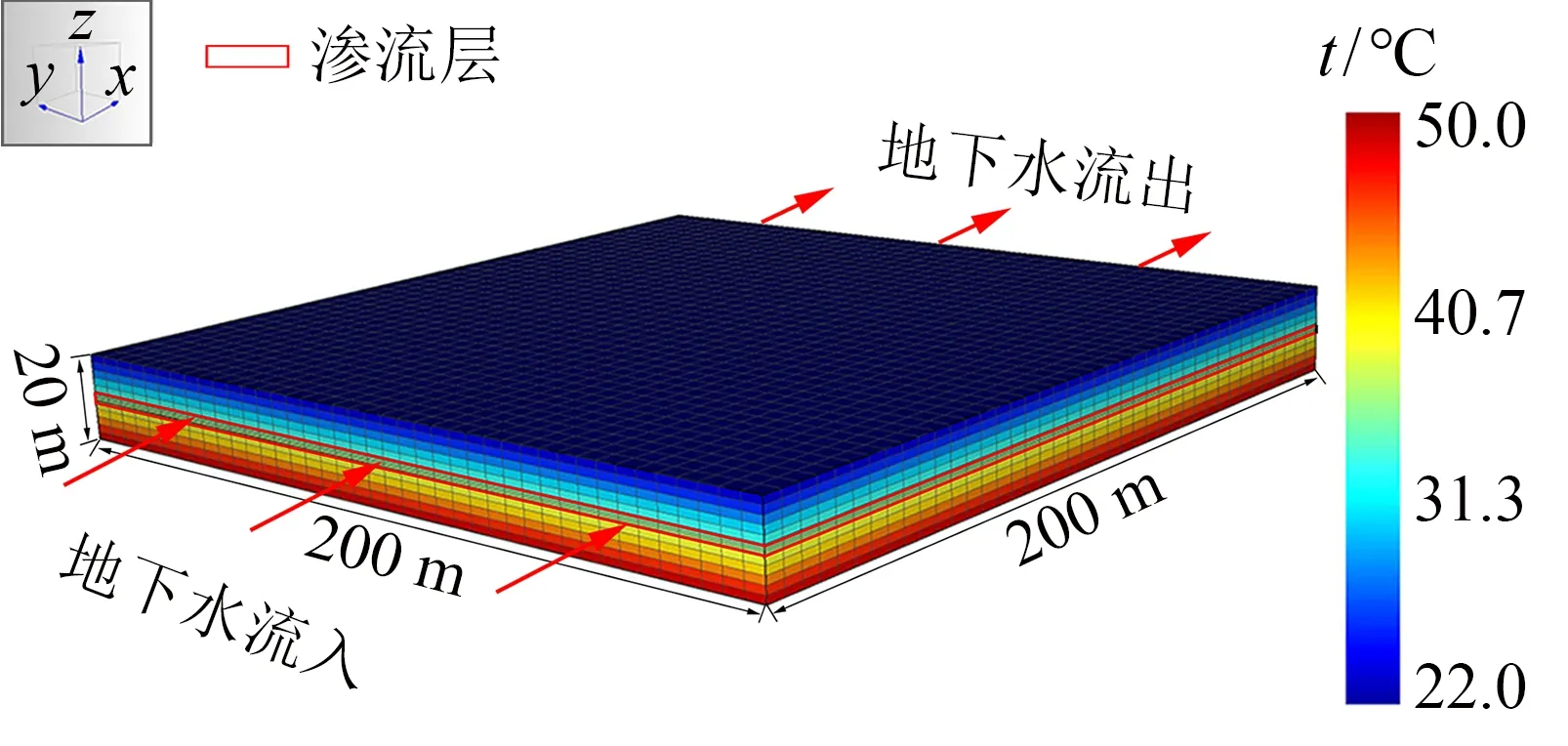
图2 水热耦合模型初始状态

2.3 模拟结果和分析

各工况模拟计算至模型达到平衡，随后根据地温预测模型原理，提取各模拟工况1和2 m深度地温计算q，并将2 m深度地温作为已知地温，结合q和λ对20 m深度地温进行预测. 根据预测结果绘制预测误差与各影响因子的关系曲线如图3.

图3 预测误差与各影响因子关系

从图3可以看出，模拟数据的预测误差与各影响因子间均具有良好的相关关系，对v、 Δt、h与预测误差进行曲线拟合，对应的相关系数分别为0.973 5、 0.999 2、 0.998 7. 当Δt为0时，地下水与流经区域不会产生热交换，此时的预测误差最小，为0.28%，说明理想情况下地温预测模型的准确性较高. 随着v、 Δt、h的增大，模型预测误差均有明显增大. 在上述模拟工况中，当v为250 m·a-1、 Δt为10 ℃、h为2 m时，模型预测误差达到最大值11.37%，可见Δt在3种影响因子中起主导作用.

渗流会导致热能沿水流方向发生横向迁移，进而影响地温分布. 为更好地分析渗流对地温预测的影响，假设热能横向迁移仅存在于渗流层，此时渗流会导致地温预测模型中的q产生变化.当渗流产生热损失时，q与无渗流时的值相比偏小； 当渗流产生热补给时，则q与无渗流时的值相比偏大.渗流层的换热形式有地下水的热传导、 地层的热传导、 地下水与地层的热交换和地下水流动造成的对流换热等.按稳态传热的概念，可用总热阻R来表征热量在热流路径上遇到的阻力，此时λe可表示为：

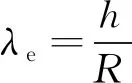
(4)

在实际计算中，λe可表示为：

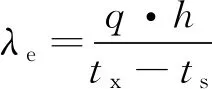
(5)

式中：ts为预测的渗流层顶板地温，单位为℃；tx为渗流层底板模拟地温，单位为℃.

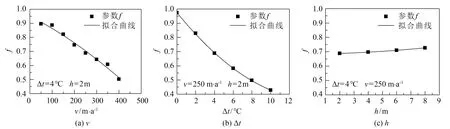
图4 参数f与各影响因子关系

f=1.244-0.001v-0.078Δt-0.009h-(5.46×10-7)v2+0.002(Δt)2+0.001h2

(6)

应用λe进行地温预测模型计算，之后再次对20 m深度地温进行预测. 预测结果表明，各模拟工况的最大预测误差减小到5.11%，证明当存在渗流影响时，使用λe的模型预测结果更为准确，此时可用fλs作为渗流层热导率参与模型计算，λc可表达为：

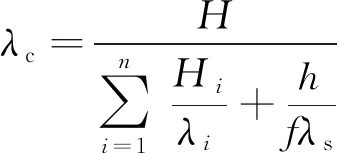
(7)

式中：n为地层数量；Hi为第i个非渗流地层厚度，单位为m；λi为第i个非渗流地层的热导率，单位为W·m-2.

3 后埔地热田地温预测

3.1 研究区浅层地温特征

采用浅层测温法在研究区布置测温点43个，点位间距为50～100 m，编号为hp01～hp43. 浅层地温调查中记录1～2 m深度地温、 热导率、 点位标高、 地下水位、 地层岩性等数据. 图5为研究区2 m深度等温线图. 研究区2 m深度温度等值线轮廓呈不规则椭圆状，长轴近似南北方向，南北方向长约600 m，东西方向宽约200 m. 2 m深度地温在24～41 ℃之间. 其中，hp06点位温度超过40 ℃，hp01、 hp07和hp09点位温度超过30 ℃，上述4个点位一起构成高温中心； hp27点位温度达到29 ℃，形成次高温中心. 浅层地温调查结果显示后浦地热田的地热异常现象明显.

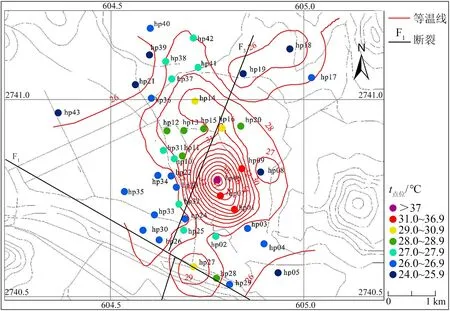
图5 研究区2 m深度等温线图

利用1和2 m深度实测地温计算研究区的q，并绘制浅层热流密度分布云图，如图6所示. 图6显示的地温异常范围与图5基本相同. 二者不同之处在于，图6显示地温异常现象最明显的区域出现在hp16点位附近，hp21点位处显示出明显的地温异常，hp27点位处的地温异常不明显. 图5和6都显示出F1断裂和F3断裂对异常地温分布的控制.

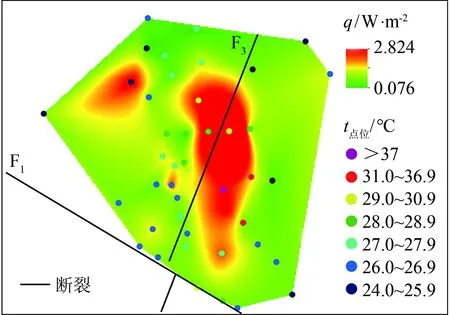
图6 研究区浅层热流密度分布云图

3.2 地温预测结果和讨论

应用地温预测模型对后埔地热田20 m深度的地温进行预测.t′取2 m深度地温实测数据；H由点位标高决定，以hp06点位标高作为基准换算；λc由地层岩性决定，2 m深度以内采用实测原位热导率数据，2 m深度以下采用室内热导率试验数据. 根据现场试验，砂层中的v约为295 m·a-1，地下水主要由莲花溪补给，水温为26 ℃.

图7为研究区20 m深度预测等温线图，预测温度在25～47 ℃之间. 其中，hp06、 hp07和hp16点位温度较高，分别为47.3、 44.5和47.6 ℃，hp06和hp16形成两个高温中心，多数高温点位均处在两个高温中心周围. 北西方向围绕hp21存在1个次高温中心，预测温度为35.9 ℃. 等温线有向北西方向扩张的趋势，显示出两条断裂对于地温分布的控制.

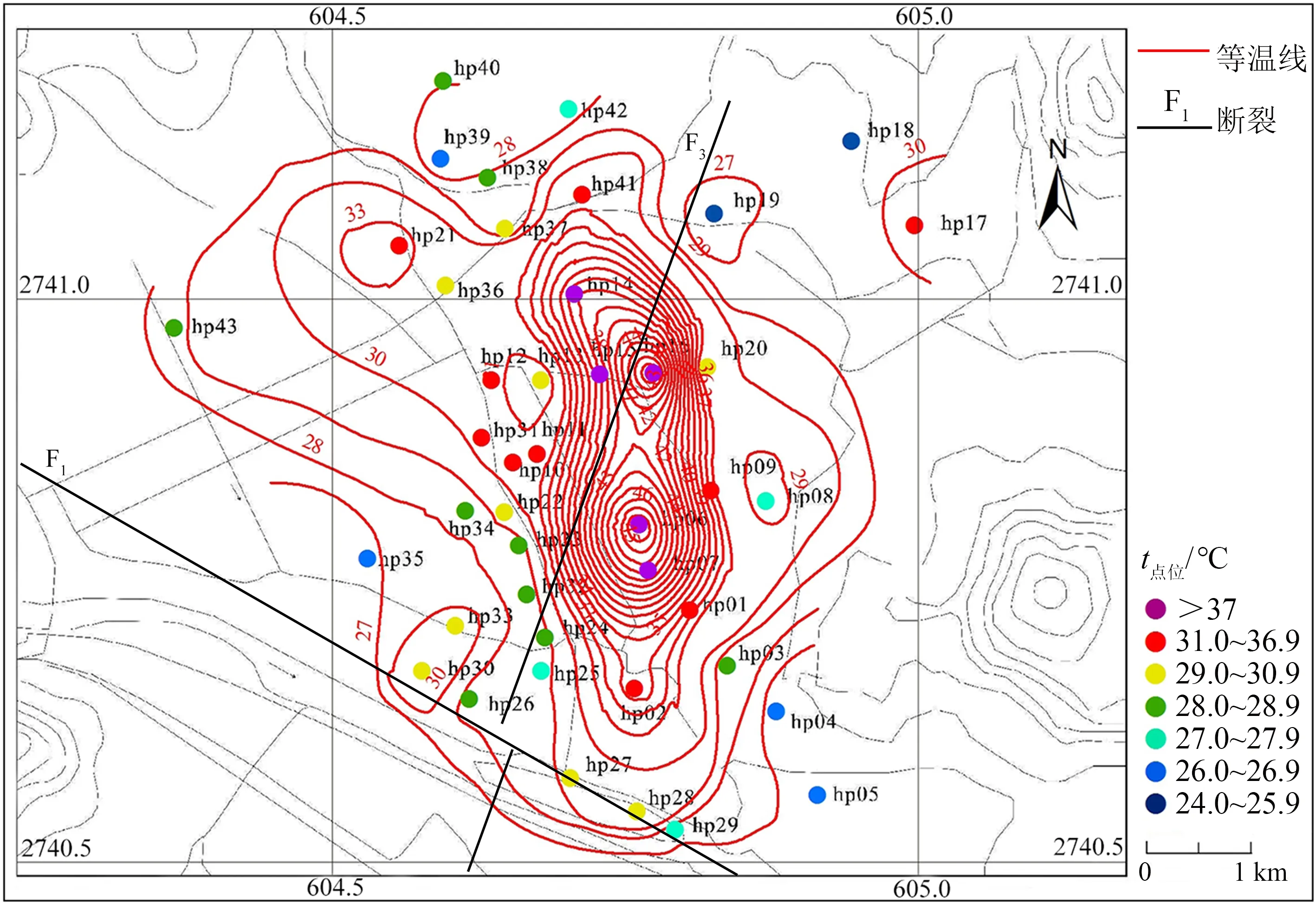
图7 研究区20 m深度预测等温线图

对比图5、 6、 7，尽管3张图描述的后埔地热田地热异常区范围大致相同，但仍有区别. 图5显示，hp06点位为高温中心，hp27点位为次高温中心，hp21点位显示不出地温异常； 图6显示，地温异常最突出的区域在hp16点位附近，hp21点位显示出较明显的地温异常，hp27点位的地温异常不明显； 图7显示hp06和hp16都属于高温中心，hp21为次高温中心，hp27地温异常不明显. 究其原因，2 m深度等温线取决于浅层实测地温，浅层热流密度取决于浅层测温的综合结果，考虑不同深度地温和地层热物性影响； 而恒温层以下的预测等温线取决于浅层测温结果和地层、 环境、 渗流等综合因素. 从原理上看，恒温层以下的预测温度考虑的因素更多，在反映地热异常方面相较于前者应更加准确.

为验证地温预测模型能力，对比典型点位20 m深度实测地温(t实测)和预测地温(t预测)数据，如表2所示. 典型点位实测和预测地温的绝对误差范围为0.2～3.3 ℃，相对误差范围为0.5%～7.8%，平均相对误差为4.2%，有渗流影响的点位平均相对误差为5.2%，两个高温中心hp06和hp16的相对误差分别为5.3%和6.2%. 有渗流影响的点位预测误差没有明显增大，说明渗流影响带来的误差已基本消除，应用λe对于降低模型预测误差是有效的. 综合来看，场地验证结果证明地温预测模型效果良好，同时证明恒温层以下的预测地温相较于2 m深度地温和浅层热流密度更能反映地热异常的实际情况.

表2 典型点位20 m深度实测和预测地温

4 结语

1) 在考虑渗流影响的地温预测模型中，渗流速度、 地下水与流经区域的温差、 渗流层厚度与预测误差呈强相关关系，温差在3种影响因子中起到主导作用，λe的应用使模型预测误差明显减小；

2) 后埔地热田地温预测结果平均相对误差为4.2%，考虑渗流影响的点位平均相对误差为5.2%，恒温层以下的预测地温相较于2 m深度地温和浅层热流密度更能反映地热异常的实际情况；

3) 后埔地热田温度异常区形态呈不规则椭圆状，长轴近似南北方向，能够体现出F1和F3两条断裂对地温分布的控制，hp06、 hp16等点位附近地热异常现象明显.