基于辛格插值模式的连续体结构拓扑优化研究*
李玉刚,杨 林
(1.贵州装备制造职业学院,贵州 贵阳 550025;2.贵州大学 机械工程学院,贵州 贵阳 550025)
0 引 言
拓扑优化是指在设计领域内寻求最佳的材料分布,从而使所得到的结构达到最佳的或规定的性能。
自1988年BENDSOE M P等人[1]发表了关于均匀化方法的开创性研究论文以来,人们在此基础上又发展了各种拓扑优化方法,例如,MLEJNEK H P等人[2]提出的变密度法、ALLAIRE G等人[3]提出的水平集法及XIE Yi-min等人[4]提出的渐进结构优化法。其中,变密度法以其数学理论严谨、物理意义明确等优点,因而得到了广泛应用[5]。
HUANG Xiao-dong[6]指出了连续体结构拓扑优化问题本质上是0/1离散变量的组合优化。因此,采用变密度法将不可避免地产生在实际工程难以制造的中间密度单元[7]。BENDSOE M P等人[8]提出了采用惩罚函数法使中间变量对对应单元材料刚度的影响变小,从而使最终优化解趋于0或1。
目前,最流行的惩罚函数模式有:SIGMUND O[9]提出的固体各向同性惩罚微结构插值模式(SIMP),和STOLPE M等人[10]提出的材料属性合理近似插值模式(rational approximation of material properties,RAMP)。但因两种模式均具有单向惩罚特性,即总是以降低单元弹性模量和单元刚度来达到惩罚目的,不利于中间密度单元的消除,且易出现最终拓扑结构边界不清晰、棋盘格等数值不稳定现象[11]。
针对传统变密度法的不足,笔者提出一种基于辛格插值模式的连续体结构拓扑优化新方法,并通过算例来验证该方法对二维及三维设计域拓扑优化的可行性,从而有效弥补传统变密度法的缺陷。
1 辛格插值模式
针对传统变密度法的单向惩罚性问题,理论上如果能构造一插值模式,其既可以提高“有用”单元弹性模量和单元刚度,又可以降低“无用”单元弹性模量和单元刚度,那么,此类具有双向促进特性的插值模式比具有单向惩罚特性的插值模式更加高效、实用。
因此,笔者制定以下更加合理的中间单元处理策略:
首先,设定一参考值(对于本研究所涉及[0,1]区间内的设计变量,参考值取0.5),该参考值用以判断中间密度单元弹性模量和单元刚度的促进方式。然后,提高密度值大于0.5的单元弹性模量和单元刚度,同时,降低密度值小于0.5的单元弹性模量和单元刚度;
然后,根据以上中间密度单元处理策略构造如下辛格插值模式:
利用辛格函数[12](即sinc函数)在[0,1]区间内具有较高斜率的单调特性(可使中间密度单元快速向实体单元进化或快速向空洞单元演化),构建如下材料属性的辛格插值模式:
(1)
式中:xi—单元密度值;xmin—最小单元密度值;α(xi)—辛格插值函数;τ—双向促进因子。
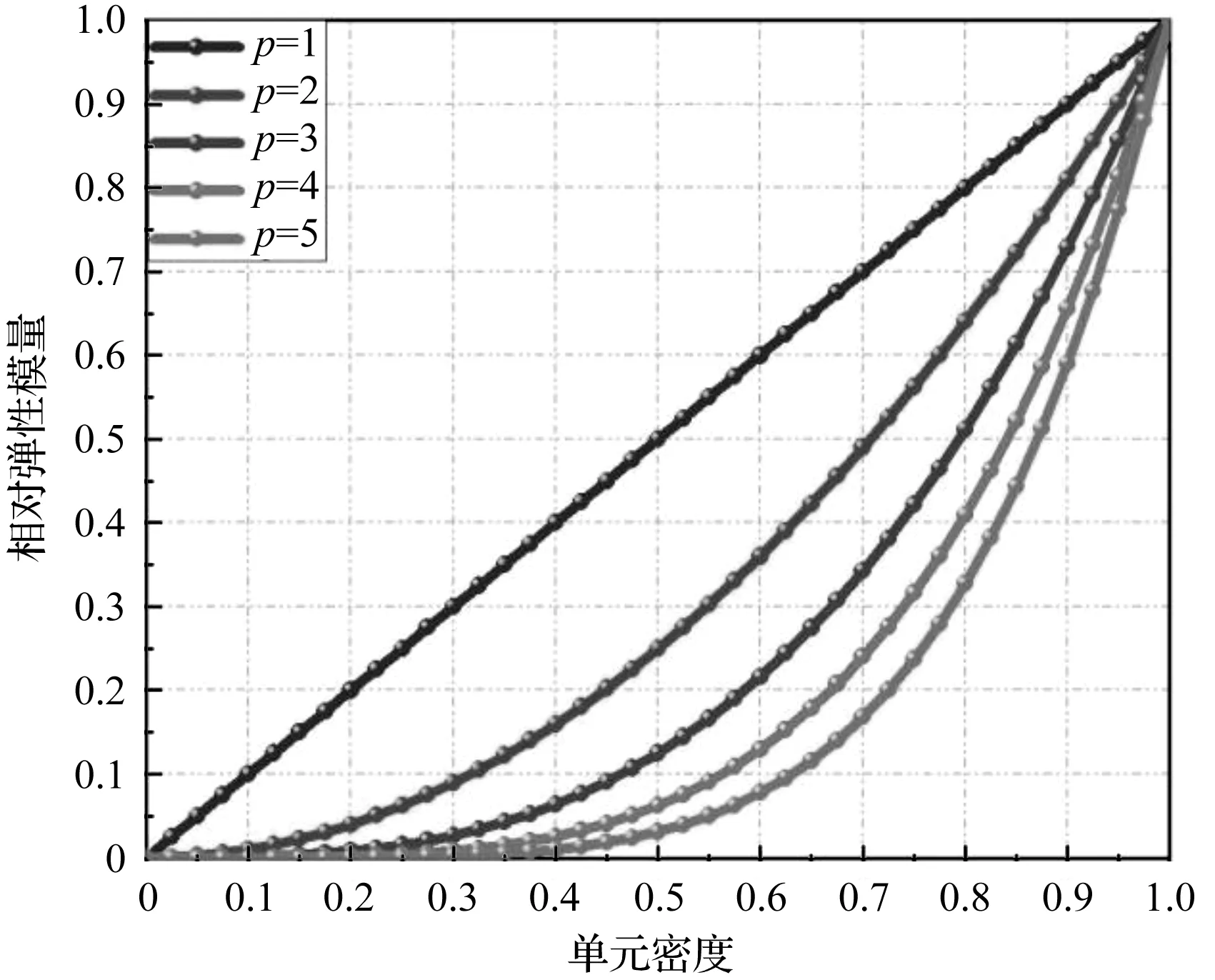
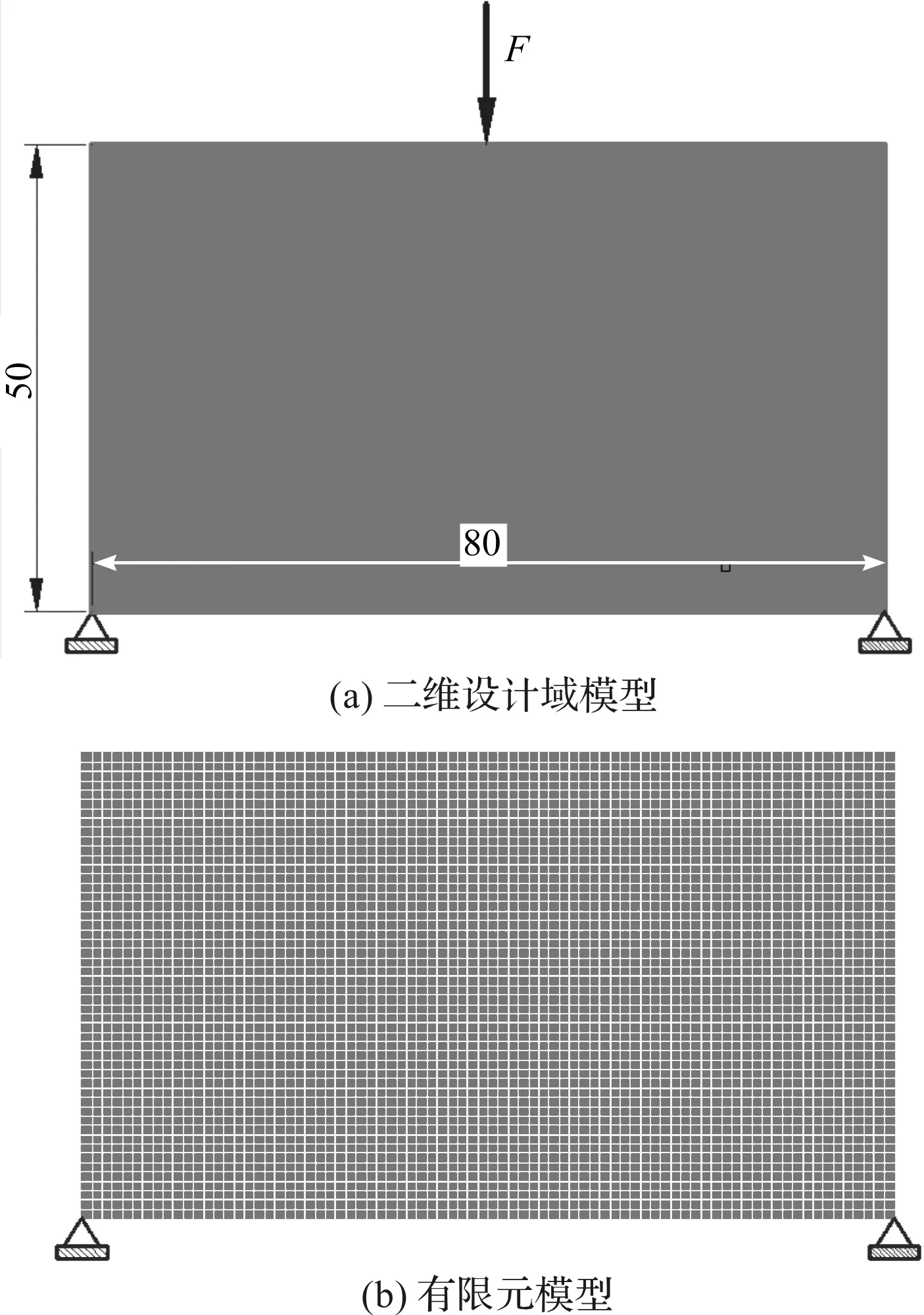
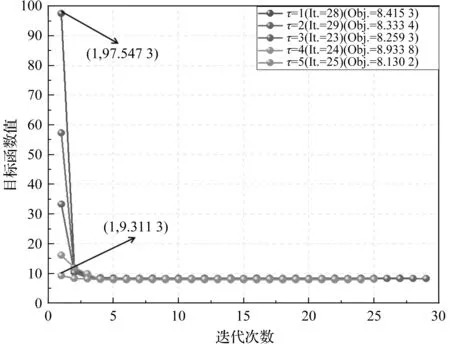
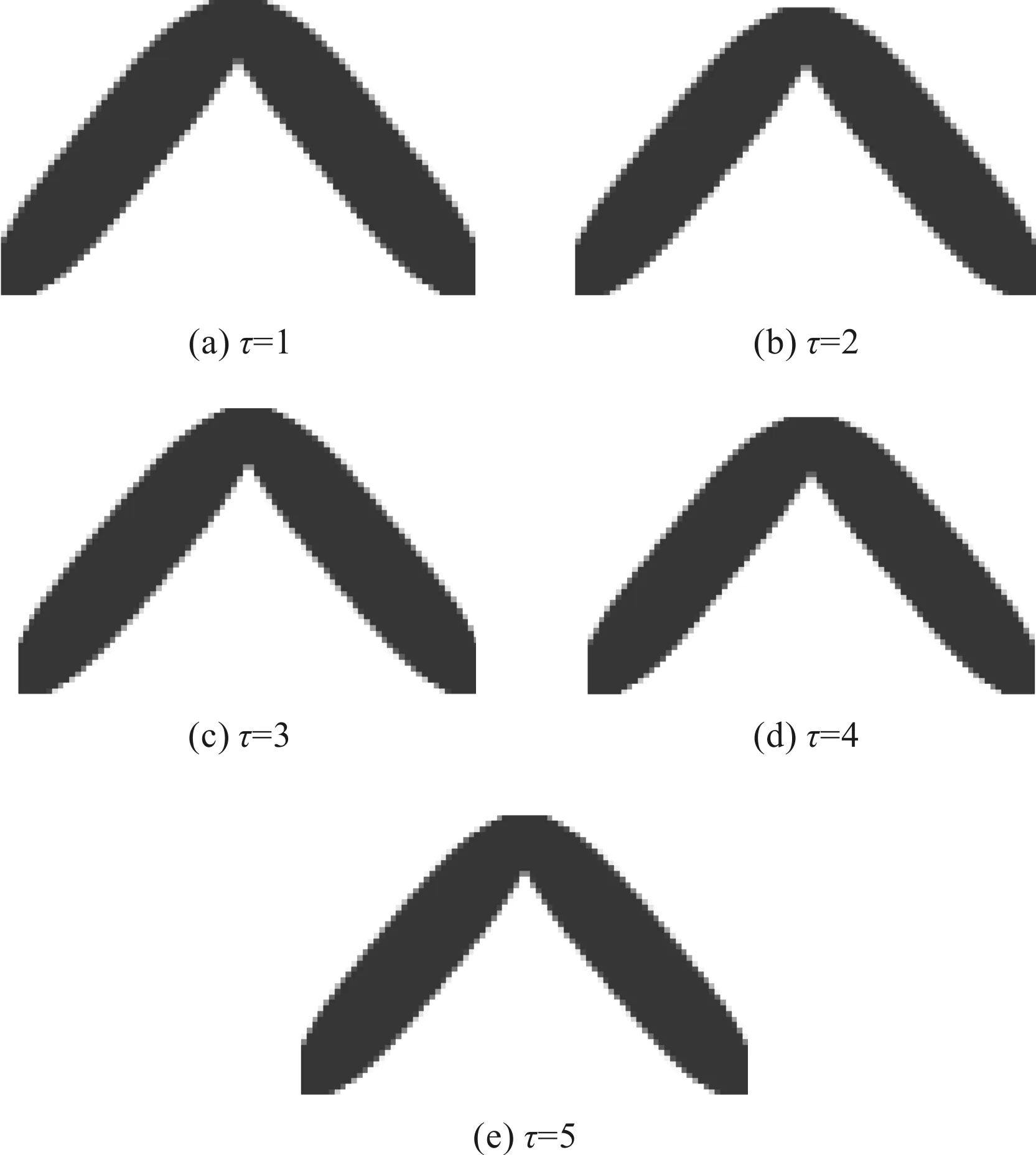
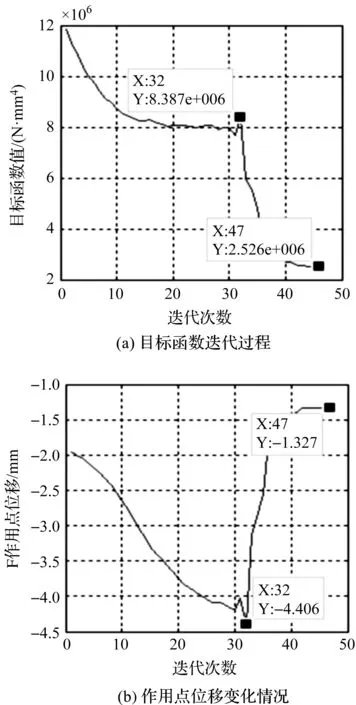
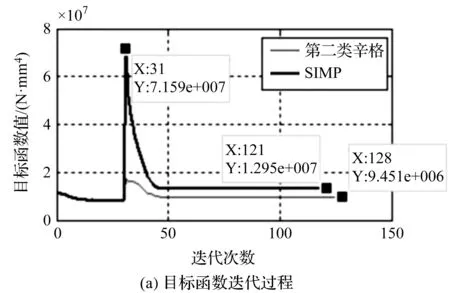
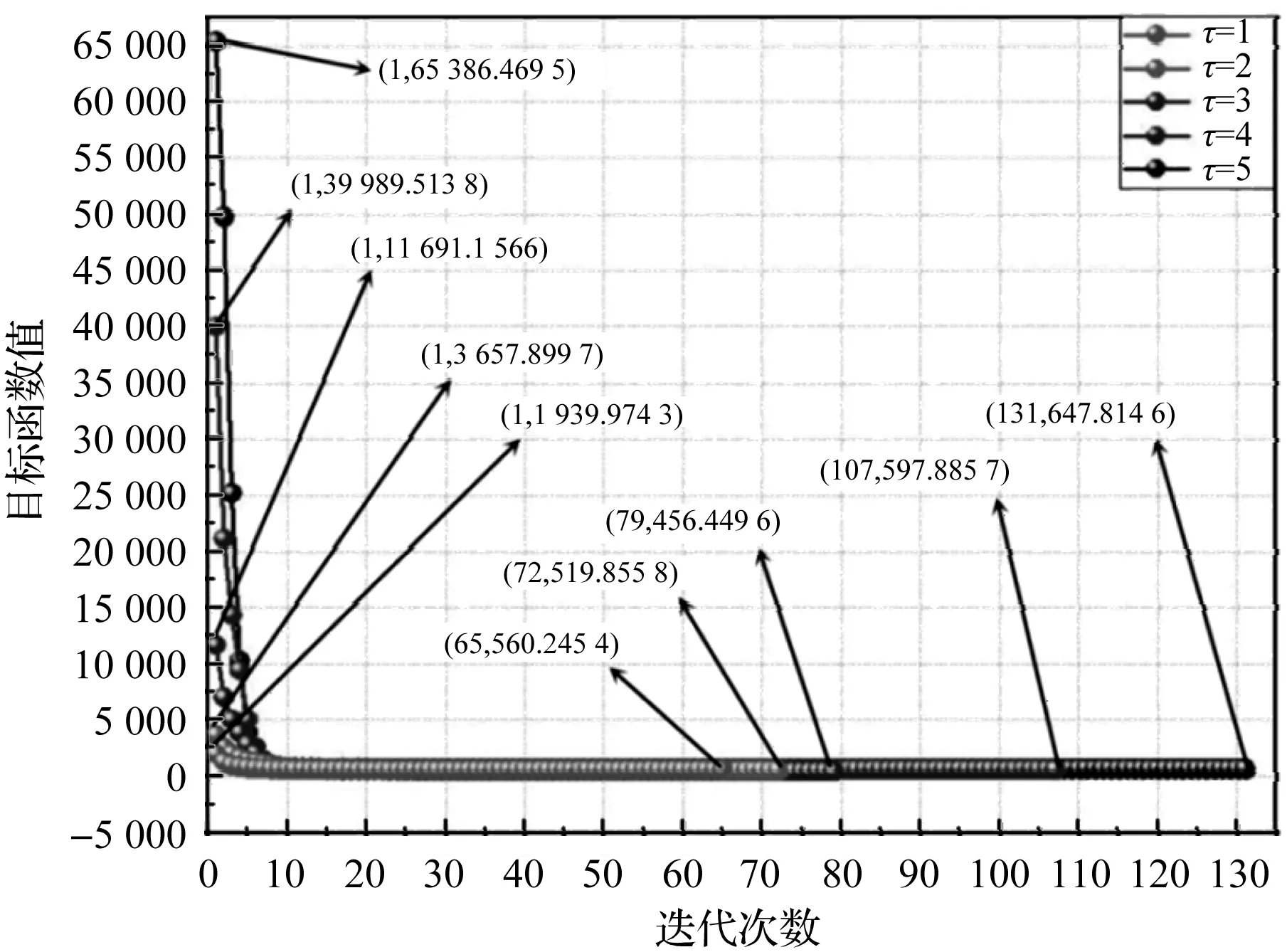
其中:τ既可促进xmin≤xi≤0.5的单元弹性模量和刚度提高,也可促进0.5 辛格插值模式双向促进效果如图1所示。 图1 辛格插值模式双向促进效果图 SIMP插值模式单向惩罚效果如图2所示。 图2 SIMP插值模式单向惩罚效果图 对比图(1,2)可知: 随着双向促进因子τ或单向惩罚因子p的增大,两种模式的惩罚或促进力度也随之增强,但SIMP插值模式的增强力度显然弱于辛格插值模式。 在基于SIMP插值模式的拓扑优化有限元分析过程中,通常利用基于单元密度设计变量的惩罚函数实现单元材料弹性模量的迭代,以达到修改单元刚度矩阵的目的。 相应地,辛格插值函数与单元刚度矩阵和弹性模量之间的关系可表示为: (2) 式中:K0—实体材料刚度;Ki—优化后单元刚度;E0—实体材料弹性模量;Ei—优化后单元弹性模量。 在拓扑优化迭代过程中,因作为设计变量的单元密度是动态变化的,相应的单元材料弹性模量或单元刚度也是动态变化的,而事实上,惩罚函数的作用仅是惩罚具有中间密度单元材料的刚度或弹性模量,所以,更合理的策略应是对上一次迭代结果中具有中间密度的单元材料的刚度或弹性模量进行惩罚,而不是总以实体材料刚度和实体材料弹性模量为标准。 因此,式(2)可优化为: (3) 相应地,在基于传统SIMP惩罚函数拓扑优化有限元分析过程中,通常采用刚度矩阵对单元密度设计变量的偏导数表示单元刚度对设计变量的敏度。 其表达式如下: (4) 但实际上,单元密度的敏度计算应满足材料本构关系,即单元密度与单元刚度和弹性模量之间应是线性关系,因此,单元刚度对单元密度设计变量的敏度应按线性关系计算,然后再利用辛格插值模式对敏度进行处理。 所以,在拓扑优化过程中,应根据单元密度值大小不断对迭代方向进行调整,这样即使不采用过滤技术,也能得到清晰边界的拓扑结构。 因此,基于辛格插值模式的敏度可表示为: (5) 以连续体结构体积约束下,总体柔度最小化为优化目标,在给定边界条件和载荷工况下,基于辛格插值模式的优化模型为: (6) 式中:f—结构总体柔度函数;ki—第i单元优化后的刚度矩阵;ui—第i单元优化后的位移向量;V—优化后结构总体积;Vi—单元体积;V*—目标优化体积;F—作用力;K—总刚度矩阵;U—总位移矩阵; 其中:取xmin=0.001 5,以避免总刚度矩阵奇异。 结合式(5),刚度可采用两种方式计算。其中,一种方式是只对敏度进行辛格插值,笔者称该方法为第一类辛格插值法,如下式所示: (7) 另一种方式是既对敏度进行辛格插值,又对刚度进行辛格插值,笔者称该方法为第二类辛格插值法,如下式所示: (8) 构造问题(6)的移动渐进算法(the method of moving asymptotes, MMA)[13,14]求解表达式为: (9) 为方便表达,此处令: (10) (11) 并令t表示迭代次数,则展开模型表达式如下: (12) 其中: (13) 结合对偶理论,将移动近似凸子问题(13)转换成易于计算求解的对偶问题,同时令λ表示对偶设计变量,则有: (14) 其中: (15) 其迭代终止条件如下: (16) 其中:取δ=0.01。 基结构尺寸为80×50,厚度为1,材料弹性模量为E=1,泊松比为0.3,划分为60×30个矩形四节点单元;固定点为左下角边界点和右下角边界点,且采用自由度全固定约束;集中载荷F=1,作用于上边界中点;求体积约束分数为0.4时的结构最优拓扑。 为简化计算,该例中所有设计参数均按无量纲处理,且不会影响优化有效性。 二维设计域模型及有限元模型如图3所示。 图3 二维设计域及有限元模型 数值不稳定现象[15]是影响连续体结构拓扑优化结果质量的关键因素之一。 在传统变密度方法拓扑优化过程中,通常采用空间敏度过滤技术以消除优化过程中存在的数值不稳定现象,但该技术易使敏度在其过滤半径内均匀化,即最终拓扑结构的拓扑边界易出现模糊现象。 不采用过滤技术时,不同τ值的拓扑结果如图4所示。 图4 不采用过滤技术时,不同τ值的拓扑结果 根据图4,不采用过滤技术时,辛格插值模式所得优化拓扑结果结构边界清晰,即未出现网格依赖性、棋盘格等现象,且τ取不同值时的拓扑结构基本相同,所以双向促进因子的取值对拓扑结果影响不大。 相应的,τ取不同值时的优化迭代过程如图5所示。 图5 τ取不同值时的优化迭代过程 从图5可以看出:随着迭代步数和τ取值的增加,目标函数值变化趋势基本相同,均呈现出快速减小的规律,且最终收敛值趋于一致; 另外,τ=1~5时的收敛速度也基本相同,且均在第4步迭代后进入稳定收敛状况。不同的是,随着τ取值的增加,初始目标函数值快速减小(τ=1时,f1=97.543 7;τ=5时,f1=9.311 3)。 接下来,在辛格插值模式优化过程中,笔者同时采用空间敏度过滤技术(本例中,过滤半径取1.2)。 同时采用敏度过滤技术时,不同τ值的拓扑结果如图6所示。 图6 同时采用敏度过滤技术时,不同τ值的拓扑结果 根据图6,在辛格插值模式优化过程中,同时采用敏度过滤技术,双向促进因子τ取不同值时,优化拓扑结果结构边缘模糊、不清晰,与不用过滤方法时所得最终优化后拓扑结构基本一致。 二维设计域尺寸为40 mm×20 mm,厚度为1 mm,材料弹性模量E=200 GPa,划分为40×20个矩形四节点单元;左边界全部采用固定约束;集中载荷F=9 000 N作用于右边界中点。 为了简化计算过程,上述设计参数按无量纲处理,求具有最小体积和最大刚度的结构最优拓扑,设初始单元密度为0.9。 该算例二维设计域模型及有限元模型如图7所示。 图7 二维设计域及有限元模型 采用第一类辛格插值法所得最终拓扑结构如图8所示。 图8 第一类辛格插值法所得最终拓扑结构 采用第二类辛格插值法所得最终拓扑结构如图9所示。 图9 第二类辛格插值法所得最终拓扑结构 采用SIMP法所得最终拓扑结构如图10所示。 图10 SIMP法所得最终拓扑结构 对比图(8~10)可知:第二类辛格插值方法所得最终拓扑结构与SIMP方法相似,而第一类辛格插值方法拓扑结构更加清晰、简洁。 第一类辛格插值法优化目标函数值、作用点位移、体积及柔度变化曲线,如图11所示。 图11 第一类辛格插值法优化目标函数值、作用点位移、体积及柔度变化曲线 由图11可知:第一类辛格插值方法优化结果体积为初始体积的0.264倍,在优化过程中,开始时不进行辛格插值计算迭代,直到目标函数值趋于稳定(相对误差小于0.000 01),得到数学上最优解,迭代步30步为转换步,之后开始采用辛格插值第一类辛格插值法优化策略,以消除中间密度单元;自30~32步之间迭代有波动,这是由于对中间密度单元进行双向调整所致,之后计算趋于稳定。 因进行双向调整,更合理地分布了材料,使得在体积相对一致的情况下,目标函数值快速下降,结构柔度值快速减小,增大了刚度,同时在相同外力作用下,作用点位移快速从-4.406 mm变化到-1.327 mm。 第二类辛格插值法和SIMP方法优化目标函数值、作用点位移、体积及柔度变化曲线,如图12所示。 图12 第二类辛格插值法和SIMP方法优化目标函数值、作用点位移、体积及柔度变化曲线 由图12可知:第二类辛格插值方法和SIMP方法优化拓扑近似,迭代收敛结果大小近似,收敛步数亦相近,但SIMP方法计算数值波动比第二类辛格插值方法大。 综上所述,与第一类辛格插值法方法优化所得目标函数值(2.526e6)相比,第二类辛格插值方法、SIMP方法所得的目标函数值(9.451e6,1.295e7)要大数倍。所以,第一类辛格插值法方法更加敏捷,可得到更小的目标函数值。 三维设计域的尺寸为60×30×10,材料弹性模量为E=1,泊松比为0.33,划分为60×30×10个立方体八节点单元;一端完全约束,且在另一端自由边缘向下施加垂直的分布载荷F;求体积约束分数为0.4时的结构最优拓扑。 为简化计算,该算例中所有设计参数均按无量纲处理,且不会影响优化的有效性。 该算例三维设计域模型及有限元模型分别如图13所示。 图13 三维设计域及有限元模型 为了证明所提方法在处理三维问题中的有效性,笔者采用基于辛格插值模式的MMA算法进行三维设计域的拓扑优化,研究双向促进因子τ取不同值时的拓扑优化结果及优化计算的迭代收敛情况。 τ取不同值时的最终拓扑结构如图14所示。 图14 τ取不同值时的最终拓扑结构 由图14可知:采用基于辛格插值模式的MMA算法进行三维设计域拓扑优化,并经isosurface函数后处理,所得拓扑结构可靠、清晰且不失真,可直接利用3D打印技术制造;且双向促进因子τ=3和τ=4时的最终结构拓扑较τ=1、τ=2及τ=5时更简洁。 相应的,τ取不同值时的优化迭代过程如图15所示。 图15 τ取不同值时的优化迭代过程 由图15可知:随着τ取值的增大,目标函数初始值不断增大,迭代次数也随之增多,但目标函数值却呈现出先减后增的趋势,且当τ=3时,可以取得最小目标函数值456.449 6;该趋势与辛格插值模式的双向促进特性相吻合。 针对传统基于变密度法的求解方法的单向惩罚特性缺陷,笔者提出了一种求解连续体结构拓扑优化问题的新方法,并结合算例验证了该方法对二维及三维设计域拓扑优化的可行性。 研究结论如下: (1)与以往采用过滤技术以消除拓扑优化过程中存在的数值不稳定现象的技术相比,在不采用过滤技术的情况下,该新方法既可消除数值不稳定现象,又可得到具有清晰边界的拓扑结构; (2)在二维设计域拓扑优化迭代过程中,与传统变密度拓扑优化求解方法相比,该新方法所得的最终结构拓扑边界更加清晰,初始目标函数值、迭代步数和最终目标函数值更小;且与第二类辛格插值法和SIMP插值法相比,第一类辛格插值法更加敏捷,可得到更小的目标函数值;在三维设计域拓扑优化迭代过程中,该新方法所得拓扑结构可靠、清晰且不失真。 在后续的研究工作中,笔者将进一步开展该新方法与3D打印技术有效结合的关键技术研究,并将其应用于工程实践。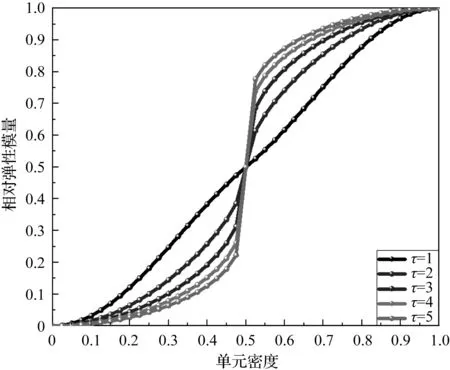
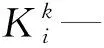
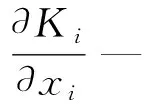
2 基于辛格插值模式的优化模型及算法
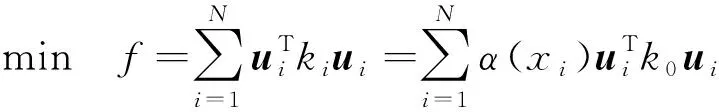
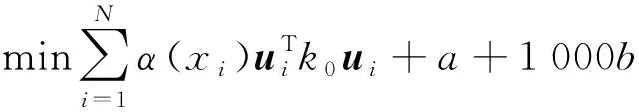
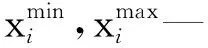
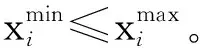
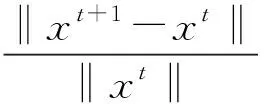
3 算 例
3.1 算例一

3.2 算例二
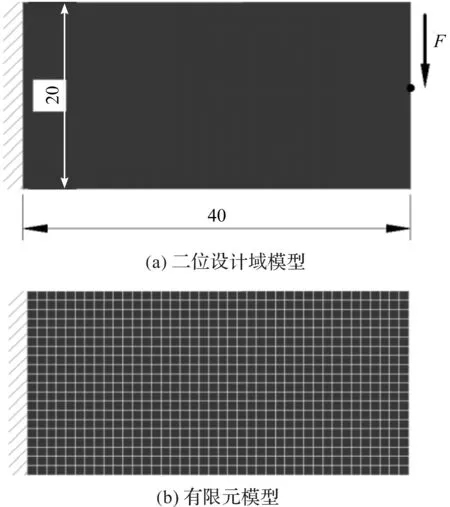



3.3 算例三
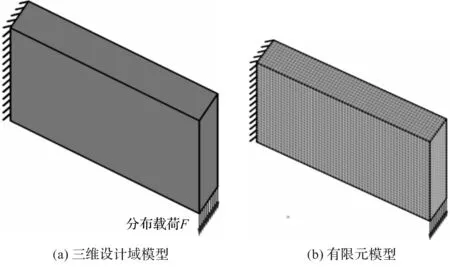

4 结束语

