采样点数对圆柱体计算尺寸评定结果的影响*

赵则祥,史鑫朝,赵新宇,席建普

(1.中原工学院 机电学院,河南 郑州 450007;2.中原工学院 计算机学院,河南 郑州 450007)

0 引 言

圆柱体尺寸除了常用的两点尺寸(点对尺寸)[1]外,为了使图样标注含义更加清晰明确,适应机械制造业向精密制造、智能制造方向发展趋势,新一代产品几何技术规范(geometrical product specifications, GPS)中,对圆柱体尺寸进行了系统的规定。

在该规范中,规定了以下尺寸:(1)局部尺寸。包括两点尺寸、球面尺寸、截面尺寸、部分尺寸;(2)全局尺寸。包括直接全局尺寸(最小二乘直径、最小外接直径、最大内切直径和最小区域直径)和间接全局尺寸;(3)计算尺寸。包括周长直径、面积直径、体积直径;(4)统计尺寸。包括最大尺寸、最小尺寸、平均尺寸、中位尺寸、极值平均尺寸、尺寸范围、尺寸的标准偏差。

有关上述尺寸的含义见文献[2]4-11。

按照上述尺寸的规定,设计人员可以根据零件功能需要,在图样上标注相适应的尺寸;检验人员可依据图样上标注的尺寸,选择相应的测量与评定方法。

根据文献[2]7-9中有关圆柱体计算尺寸的含义,计算尺寸较合适的测量与评定方法为:在柱坐标测量仪上对圆柱体要素采用圆周法进行轮廓提取,并基于其对应的评定模型进行评定。采用圆周法对圆柱体要素对轮廓进行提取时,需要设置每个圆周的采样点数。采样点数设置过多,将造成信息冗余,测量和评定时间较长,测量过程中可能引入粗大误差;采样点数设置过少,将造成信息不足,提取的轮廓不能代表圆周要素的实际面貌。

采样点数不仅对圆柱体计算尺寸的评定结果有影响,对圆度误差等圆柱体几何误差的评定结果也具有影响,一些学者对此进行了研究。

谢梦敏等人[3]采用最小区域圆法(minimum zone circle, MZC)的圆度误差评定方法,对圆度误差检测精度进行研究,得出了不同采样点数对圆度精度的影响规律。郑育军等人[4]在三坐标测量机上,对不同对象的圆进行了不同点数的均匀分布采样,采用最小二乘法(least squares circle, LSC)评定了其圆度,并对其结果进行了分析总结。文学等人[5]提出了基于粒子群算法(particle swarm optimization, PSO)及遗传算法(genetic algorithm, GA)的三测点角度优化策略,研究结果表明,采用该策略提升了回转件圆度信息的测量精度。赵前程等人[6]对圆度测量中测量点数的确定进行了研究。林志熙等人[7]对具有最少采样点的圆度误差测量进行了研究。陈隆德等人[8]对圆度误差测量中测点数的确定进行了研究。郑鹏等人[9]通过计算机模拟分析与工件实测,对圆柱度精确测量进行了研究,研究得出结论,圆柱度精确测量评定的关键是提高轴向采样频率和采样面密度。CHAN F M M等人[10]使用坐标测量机测量了圆柱体截面,研究了测量时其对采样策略的影响规律,确定了采样点数和计算结果之间的关系。GAPINSKI B等人[11]研究了测量点数和圆度偏差类型对测量结果的影响,并给出了关于测量点数的建议。MIAN S H等人[12]采用灰色关联度分析法(grey relation analysis, GRA)和优劣解距离法(technique for order preference by similarity to ideal sulution, TOPSIS),估计出了圆柱体最佳的采样点数分布方案、采样点数,并得到了其评定算法。SUMMERHAYS K D等人[13]对内圆柱面的离散采样点模型进行了优化。

上述有关采样点的问题研究,主要是基于对圆柱体的几何误差评定结果的影响展开的,其对圆柱体计算尺寸评定结果的影响是不相同的。

因此,笔者将通过用折线和弧线两种方法表征圆周轮廓,从理论和实验两方面系统研究采样点数对圆柱体计算尺寸评定结果的影响,以便计算尺寸测量时选取较合适的圆周轮廓表征方法和采样点数,为标准GB/T 38762.1—2020在机械制造业的贯彻实施提供技术支持。

1 轮廓要素提取与径向尺寸确定

1.1 轮廓要素的提取

当在圆柱度仪上采用圆周法对被测圆柱体进行轮廓提取时,在轮廓提取前,通常要对被测圆柱体进行调心和调平处理(即被测圆柱体的轴线与圆柱度仪的回转工作台的轴线间的平行度误差尽可能小,被测圆柱体的第一个圆周轮廓的最小二乘圆圆心与回转工作台的轴线间的偏心量尽可能小);

调心调平后,还需对圆柱度仪设置相关参数,如圆周轮廓的采样点数、两相邻圆周轮廓的轴向间距、圆周轮廓数、是否滤波、滤波参数等;之后,即可开始对被测圆柱体进行圆周轮廓提取。

1.2 径向尺寸的确定

圆柱度仪采用圆周法测量圆度误差、圆柱度误差和轴线直线度误差时,不需要测量各采样点到工作台回转轴线之间的距离。圆柱度仪是否配置线位移光栅尺均是准柱坐标测量仪,且得到的径向尺寸所形成的圆周(或圆柱体)轮廓对几何误差评定结果几乎没有影响。

但是针对圆柱体计算尺寸,采用圆周法提取圆周轮廓时,需要精密测得圆周轮廓采样点到工作台回转轴线间的径向尺寸。不配置线位移光栅尺的圆柱度仪无法精密测量径向尺寸,而配置线性位移光栅尺的测量仪,通过对标准柱或标准环以及相关模型圆周轮廓的测量,实现圆周轮廓采样点与工作台回转轴线间径向尺寸的精密测量。

笔者将标准柱放置在配置线性位移光栅尺的圆柱度仪的工作台上,经调心调平处理,将测头移至已知的标准柱的圆周位置处,提取此处标准柱的圆周轮廓。

此处以Talyrond 585LT圆柱度仪为例,由横臂配置线位移光栅传感器和电感传感器,测得的圆周轮廓第j采样点的准径向尺寸如下式所示:

(1)

式中:xB0j,yB0j—第j采样点的在x轴和y轴的坐标;xSij,ySij—第i圆周轮廓的第j采样点的x轴和y轴的坐标;m—被测圆柱体测量的圆周数;n—每个圆周轮廓的采样点数,采用等角度间隔采样;φj—第j采样点的采样间隔,rad。

笔者用标准柱消除径向测量所存在的系统误差Δρ[14]。

由于在圆柱度仪上提取圆柱体轮廓采用的是准柱坐标系,基于准柱坐标系和柱坐标系分别测得的标准柱圆周轮廓的最小二乘圆及其参数,如图1所示。

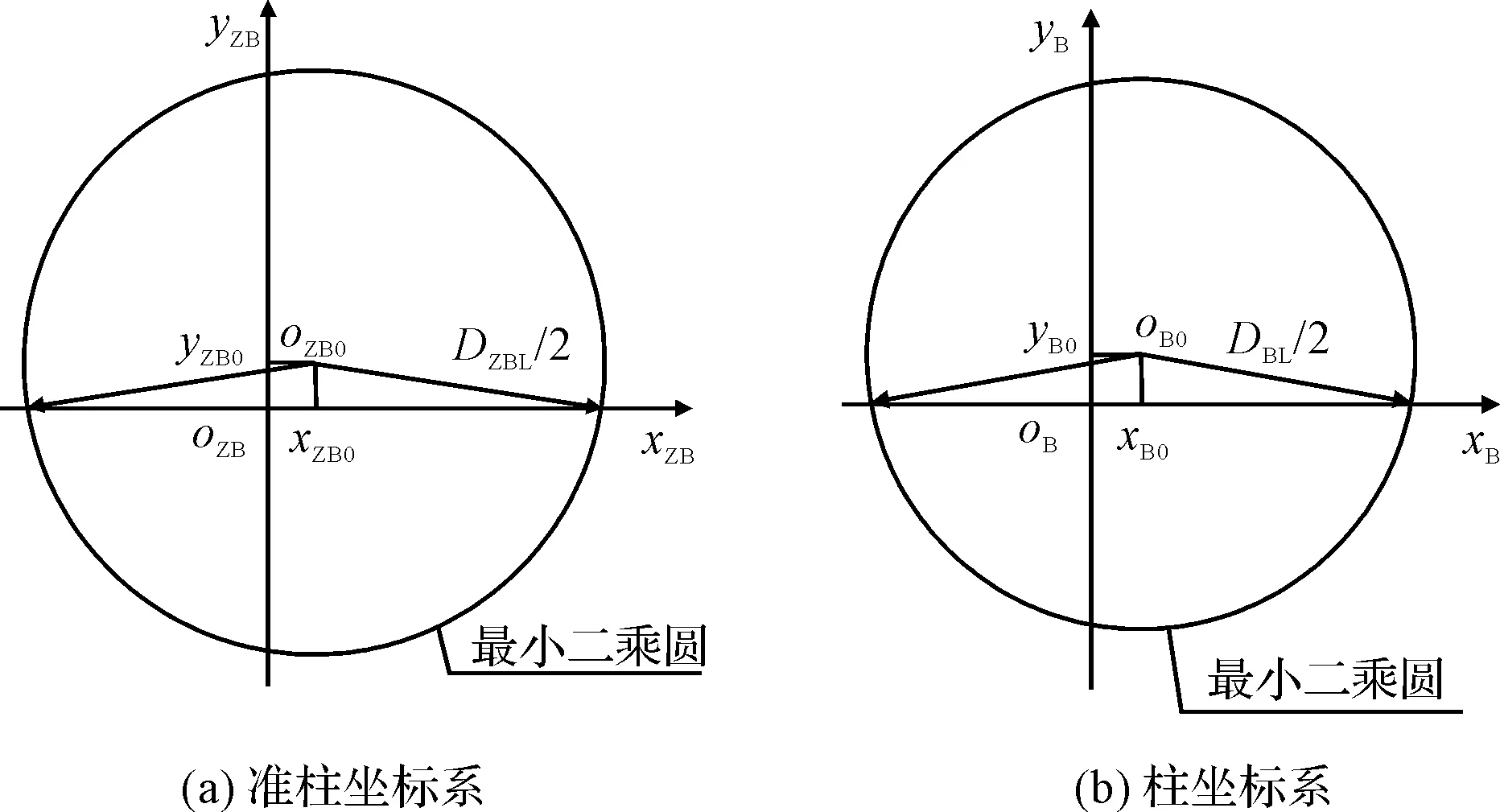
图1 最小二乘圆及其参数

由于圆周轮廓最小二乘圆圆心坐标仅与圆周轮廓各采样点的微小变动量有关,因此,图1所示两圆周轮廓的最小二乘圆的圆心坐标相同。

基于准柱坐标系提取圆周轮廓时,各采样点到工作台回转轴线的径向尺寸所存在的系统误差可表示为:

(2)

各采样点消除径向尺寸的系统误差后,可得到各采样点到工作台回转轴线的径向尺寸,即:

ρij=ρSij-Δρ,i=1～m,j=1～n

(3)

2 计算尺寸的确定

2.1 轮廓周长、面积、体积及其确定

第1至m圆周轮廓的周长、面积与体积如图2所示。

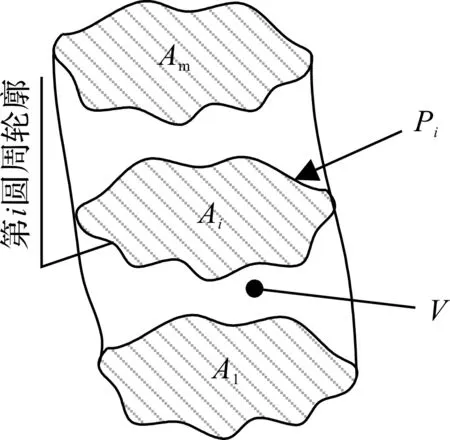
图2 周长、面积与体积图示V—第1至第m圆周轮廓间的体积;Pi—第i圆周轮廓的周长;Ai—第i圆周轮廓的面积

对于图2所示的周长,可有两种方式确定:(1)用折线(相邻点的连线)所组成的轮廓封闭线的长度,作为提取圆周轮廓的周长;(2)用弧线(两个相邻点的采样点到回转工作台轴线的径向尺寸的均值作为半径的弧)所组成的轮廓封闭线的长度,作为提取圆周轮廓的周长。

局部圆周轮廓长、面积确定方法如图3所示。

图3 局部圆周轮廓周长、面积确定方法示意图ρij,ρi(j+1)—第i圆周轮廓上第j采样点和第j+1采样点与回转台回转轴线上oi间的径向尺寸;ΔPLij—第i圆周轮廓上第j采样点和第j+1采样点间直线距离;ΔPAij—第i圆周轮廓上以ρij和ρi(j+1)的均值为半径ρaij的弧长;Δφ—两相邻采样点间的夹角;ΔALij—所示三角形的面积;ΔAAij—圆弧与两边所围的面积

已知ρij和ρi(j+1),ΔPLij和ΔALij的计算式为:

(4)

其中:

(5)

当j=n时,j+1用1代替。

ΔPAij和ΔAAij的计算式为:

(6)

其中:

ρaij=(ρi(j+1)+ρij)/2

(7)

当j=n时,j+1用1代替。

与式(4,6)相对应,第i圆周轮廓的周长和面积均有2种方式确定,如下式所示:

(8)

式中:m—被测圆柱体的圆周轮廓数。

由式(8)可得到第1～m个圆周轮廓的面积,则被测圆柱体的体积也有2种方式确定,如下式所示:

(9)

式中:Δz—两相邻圆周轮廓的轴向距离,mm。

依据圆锥台的体积计算公式,圆柱体体积的另一种计算公式如下式所示:

(10)

2.2 周长直径、面积直径、体积直径的确定

圆周轮廓的周长、面积和圆柱体体积确定后,依据其与直径的关系式,圆周轮廓的周长直径为:

(11)

式中:dPLi,dPAi—由基于直线和圆弧连接方式的圆周轮廓周长计算得到的周长直径,mm。

圆周轮廓的面积直径为:

(12)

式中:dALi,dAAi—由基于直线和圆弧连接方式的圆周轮廓面积计算得到的面积直径,mm。

被测圆柱体的体积直径为:

(13)

式中:dLV,dAV—由基于直线和圆弧连接方式的圆柱体体积计算得到的体积直径,mm;Δz—相邻两圆周轮廓的轴向间距,mm;k—两种不同体积计算方式参数,k=1,2分别表示由式(9,10)计算得到的体积;m—被测圆柱体的圆周轮廓数。

3 采样点数对评定结果的影响

3.1 对圆周和椭圆轮廓周长、面积的影响

对于圆周理想轮廓和椭圆理想轮廓,笔者均采用等角度间隔Δφ采样,其理想轮廓和替代轮廓示意图如图4所示。

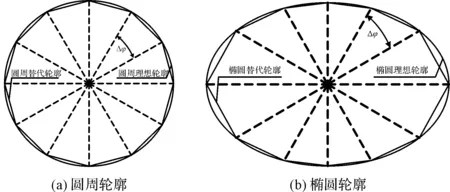
图4 理想轮廓与替代轮廓示意图

为了研究采样点数对圆周轮廓和椭圆轮廓周长、面积计算结果的影响,笔者将采样点数n设置为1 000,2 000,3 000,4 500,6 000,9 000,18 000这7种情形,在不同采样点下,按式(8)计算得到圆周和椭圆替代轮廓的周长和面积。圆周的公称直径和椭圆长轴公称轴长依据参考文献[15]公差表中的尺寸段设置,即,6 mm,10 mm,18 mm,30 mm,50 mm,80 mm,120 mm,180 mm,250 mm,315 mm,400 mm,500 mm,630 mm,800 mm,1 000 mm,1 250 mm,1 600 mm,2 000 mm,2 500 mm和3 150 mm;椭圆的短半轴长与长半轴长之比设置为0.85。

依据上述参数设置,笔者由式(8)计算替代轮廓的周长,并计算其与理想轮廓的周长的差,结果如图5所示。

图5 圆周直径(椭圆长轴长)、采样点数与周长偏差之间的关系

由式(8)再计算替代轮廓的面积,计算其与理想轮廓的面积的差,结果如图6所示。

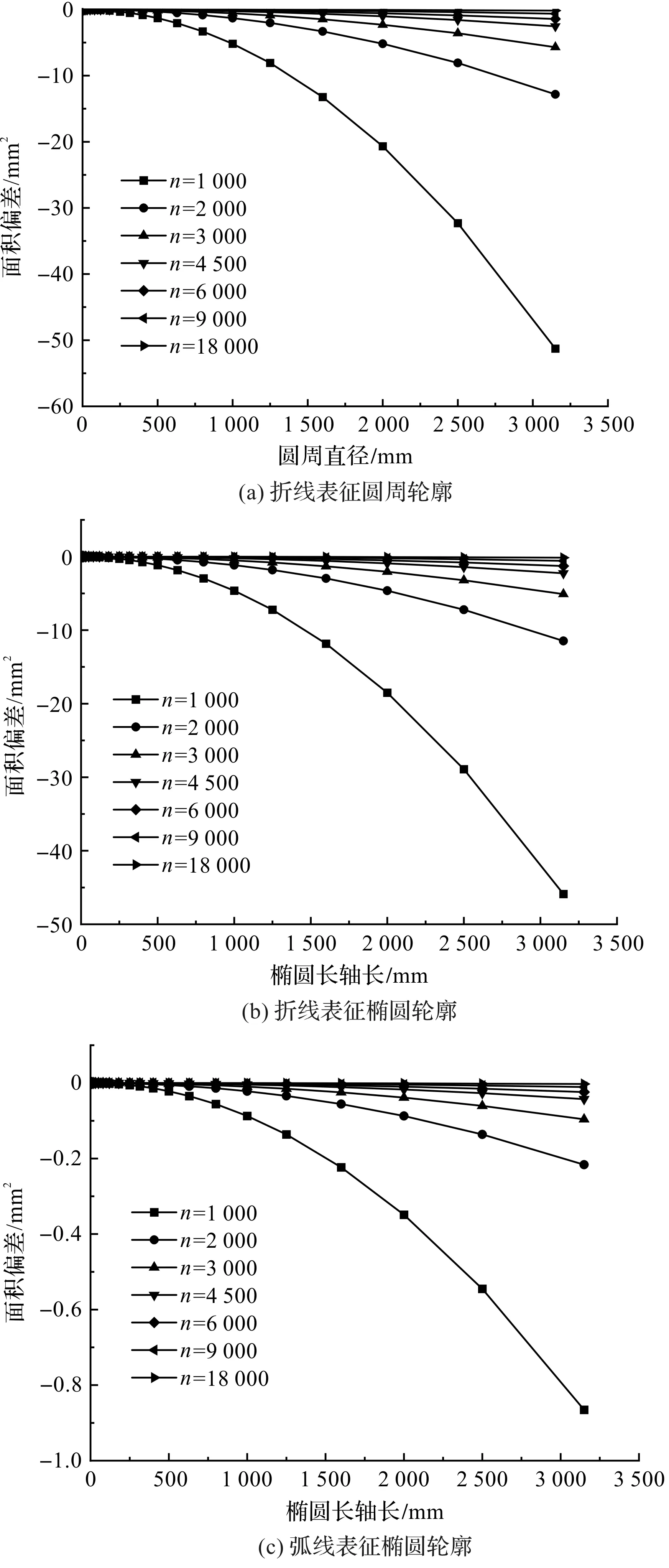
图6 圆周直径(椭圆长轴长)、采样点数与面积偏差之间的关系

由图(5，6)可以看出:在采样点数相同的情况下,公称直径越大,折线表征的圆周(或椭圆)轮廓的周长(或面积)与理想圆周(或椭圆)轮廓的周长(或面积)间的差就越大;当采用弧线表征椭圆轮廓时,弧线表征的椭圆轮廓的周长(或面积)与理想椭圆轮廓的周长(或面积)间的差的量值非常小。

同样,由图3(b)也可以看出:当两相邻采样点间的夹角Δφ较小时,用圆弧弧长ΔPAij代替椭圆弧长ΔPEij,两者相差非常小;另一方面,由Δφ和ρaij形成的圆弧面积和由Δφ与ρij、ρi(j+1)所形成的椭圆弧面积相比,其面积增加了ΔA+ij,同时也减少了面积ΔA-ij,增加和减少的面积相差较小,因此,圆弧面积与椭圆弧面积相差也比较小。

3.2 对周长直径、面积直径和体积直径的影响

由上述分析可知,当用替代轮廓表征理想轮廓时,表征轮廓与理想轮廓的周长和面积具有一定的偏差。

对于某一公称直径的圆周轮廓和椭圆半轴长的椭圆轮廓,当采样点数达到一定要求,以及替代轮廓与理想轮廓的周长和面积偏差小到其测量精度要求时,这种偏差可以忽略不计,可以用式(11～13)分别计算其周长直径、面积直径和体积直径。

由图5(a)和图6(a)所示圆周轮廓的周长和面积偏差,可得到采样点数、圆周直径与(折线表征)圆周轮廓周长直径偏差和面积直径偏差的关系,如图7所示。

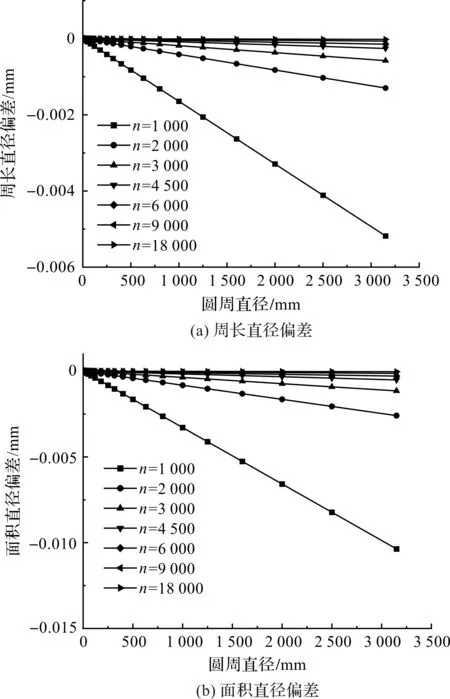
图7 圆周直径、采样点数与直径偏差之间的关系——折线表征轮廓

因图5(b,c)和图6(b,c)均是基于椭圆的,无法与直径偏差比较,但从采样点数、公称直径长(或半轴长)对其周长偏差和面积偏差的影响可知,折线表征椭圆轮廓与圆周轮廓所产生的周长和面积偏差基本上是相同的。

而用弧线表征椭圆轮廓时,由于其周长、面积偏差均较小,因此,采用弧线表征的轮廓,采样点数对其周长直径和面积直径的影响不敏感。

根据体积直径的评定模型可知,采样点数对体积直径的影响与对面积直径的影响基本相同。

4 实验与结果分析

4.1 实验

4.1.1 径向尺寸系统误差的确定

笔者使用Talyrond 585LT圆柱度仪对标准柱进行了圆周轮廓的提取,提取的圆周轮廓如图8所示。

图8 标准柱圆周轮廓及其最小二乘圆

此处采用的Talyrond 585LT圆柱度仪如图9所示。

图9 实验装置图

其中,标准柱的精密测量直径为60.897 2 mm,圆周的采样点数为18 000,圆周轮廓图的局部放大倍数为5 000。

在该次实验检测中,圆周轮廓的最小二乘圆的x和y的圆心坐标分别为0.000 1 mm和-0.000 03 mm;径向尺寸的系统误差sy=55.989 2 mm。

4.1.2 试样规格及其轮廓提取时的参数设置

笔者使用圆柱度仪对一个试样的圆柱体要素进行圆周轮廓提取,试样的规格及其轮廓提取时的参数设置如表1所示。

表1 试样规格及其轮廓提取时的设置参数

fcut—采样截止频率;upr—每周波数,undulations per revolution

依据表1中的轮廓提取参数,笔者对试样的圆柱体要素进行了轮廓提取,并由式(3)对提取的轮廓要素的径向尺寸进行消除系统误差处理。

消除系统误差,并经局部放大后的提取轮廓如图10所示。

图10 试样的提取轮廓

试样的第1、15和30圆周的轮廓如图11所示。

图11 试样的3个圆周轮廓

图(10，11)中的局部放大倍数为2 000,采样点数n=1 000。

在18 000采样点的轮廓中,每隔18个点选取1点,即可得到采样点为1 000的提取轮廓。

4.1.3 计算尺寸评定

依据式(1～13),笔者编制了计算尺寸评定程序。

为了研究采样点数对计算尺寸的影响,笔者针对采样点数为1 000,2 000,3 000,4 500,6 000,9 000和18 000的试样提取轮廓,分别进行了计算尺寸评定。对采样点数为18 000时提取的圆周轮廓分别按每隔18,9,6,4,3,2选取1点,即可得到各个采样点的提取轮廓。

该试样7种采样点数的提取轮廓的计算尺寸评定结果,如图12所示。

4.2 结果分析

由图12可以看出:用折线表征被测试样的圆周轮廓时,随着采样点数的增加,采样点数对周长直径、体积直径评定结果的影响逐渐减小,与其相比,采样点数对面积直径评定结果的影响相对较小;用弧线表征被测试样的圆周轮廓时,采样点数对周长直径、面积直径和体积直径评定结果的影响均非常小。

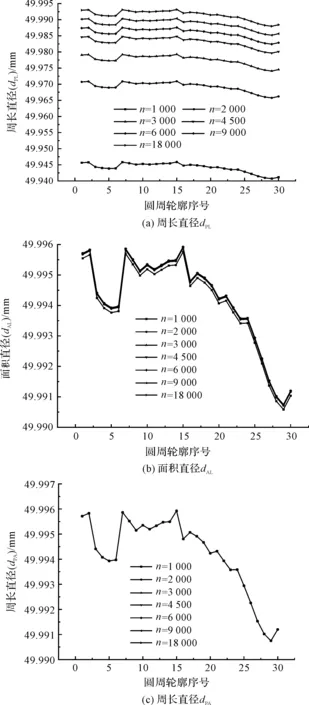
图12 7种采样点数下圆周轮廓的计算尺寸

由此可见,上述实验结果与理论分析结果比较一致。

在相同采样点情况下,为了比较不同计算公式确定的周长直径和面积直径,笔者计算出了采样点数分别为1 000,3 000,6 000,18 000时试样30个圆周轮廓的周长直径和面积直径,如图13所示。

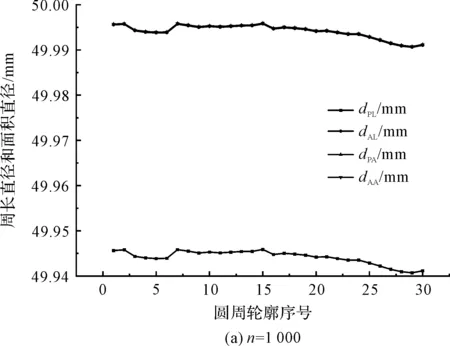
图13 试样的周长直径和面积直径

由图13可以看出:在采样点数相同的情况下,由折线表征轮廓得到的周长直径dPL值偏小(若轮廓不滤波,轮廓波动较大的情况下,周长直径也可能偏大),但由折线表征轮廓得到的面积直径dAL值和由弧线表征轮廓得到的周长直径dPA值,和面积直径dAA值间相差较小,可见采样点数对折线表征轮廓得到的周长直径dPL值影响较大。

5 结束语

针对在进行圆柱体计算尺寸评定时采样点数选取的问题,笔者提出了一种基于折线和弧线表征圆周轮廓的方法,分别建立了其周长和面积评定模型。

笔者对表征轮廓的周长、面积与其相应理论值间的差进行了理论计算,对采样点数对周长、面积和体积及其直径评定结果的影响进行了分析;用7种采样点数对圆柱体试样进行了圆周轮廓提取,基于所建立的计算尺寸评定模型,对试样的周长直径、面积直径和体积直径进行了评定;依据理论计算和实验,较系统地研究了采样点数对圆柱体计算尺寸的影响。

研究结论如下：

(1)用折线表征圆周轮廓时,采样点数对圆柱体周长直径、体积直径的评定结果影响较大,随着采样点数的增加,其对周长直径评定结果的影响逐渐减小;与其相比,采样点数对面积直径评定结果的影响相对较小;

(2)用弧线表征圆周轮廓时,采样点数对圆柱体计算尺寸评定结果的影响均非常小。

在之后的研究过程中,笔者将对圆柱体其他的几种线性尺寸进行研究,以期通过建立评定模型,研究采样点数对其评定结果的影响。