汽车起重机电液流量匹配系统非线性特性研究*

侯冠男,王 飞,杨明昆,余 聪,贾鹏硕,艾 超

(1.首钢工学院 机电工程学院,北京 100043;2.燕山大学 机械工程学院,河北 秦皇岛 066004;3.新疆工程学院 机电工程学院,新疆 乌鲁木齐 830023)

0 引 言

汽车起重机是一种装在普通汽车底盘或特制汽车底盘上的起重机[1]。

目前,汽车起重机的液压系统普遍采用传统的负载敏感(load sensitive, LS)系统。LS系统通过泵口的压力反馈,控制匹配系统需要的流量[2]。但多执行机构的LS系统执行复合运动,且处于流量抗饱和状态时,系统能耗大且多执行机构的运动协调性差[3]。

相较于LS系统,电液流量匹配系统采用流量前馈方式匹配系统流量,泵的出口压力自适应流量变化,且不用预设压力裕度,降低系统能量损失[4]。同时,电液流量匹配系统以变转速定排量泵作为动力源,具有在较宽的流量调节范围内保持高效运行的优点[5]。但由于系统存在液压泵流量非线性和非线性负载扰动等因素,使得变幅伸缩机构的控制精度不高,运动平稳性受限[6,7]。

针对流量非线性和非线性多源扰动问题,国内外专家学者开展了相关的研究[8-10],也在各自领域取得了一定的研究成果。

REN G等人[11]研究了具有内部泄漏非线性扰动的电动静液作动器的位置控制,根据稳定性和跟踪指标设计了固定增益位置控制器。该控制器在一定范围内能够补偿系统泄漏问题,保持驱动器位置控制。这对泵泄露非线性研究有一定借鉴意义。

在闭环泵控系统的非线性参数扰动方面,CHEN Ge-xin等人[12]提出了一种基于反步递推法的非线性自适应反步控制策略,通过构造系统的Lyapunov函数,获得了系统不确定参数自适应律,对系统参数扰动进行了实时在线调节,提高了该闭环泵控控制系统的精度及鲁棒性;但其研究的是整个泵控系统非线性特性及补偿控制策略。HELIAN Bo-bo等人[13]针对液压泵低转速下压力脉动非线性扰动,拟合出了液压泵流量的非线性映射,并结合了自适应鲁棒控制策略,该方法实现了较高的运动控制性能;但是其研究对象为典型的开式伺服直驱系统,研究结果对电液流量匹配系统流量非线性是否适用有待论证。张付奇等人[14]以系统稳速输出为控制目标,提出了一种基于扰动补偿的模糊自抗扰控制方法,研究了液压机械传动装置输出转速波动问题;但该研究是以整个系统为研究对象,非线性负载波动对泵的流量非线性影响无法体现。

在解决数字液压缸位置跟踪系统中不确定参数及外部扰动的问题方面,徐世杰等人[15]构造了一个Lyapunov函数及非线性控制器,实验研究表明,该控制器具有良好的鲁棒稳定性及动态特性。但是其局限于数字液压缸位置跟踪系统在外部扰动下控制性能。

上述研究均未考虑变转速电液流量匹配系统液压泵流量非线性补偿特性,不能满足汽车起重机变幅伸缩机构运动平稳性的需求。

为了改善变转速电液流量匹配系统流量控制的精度,提升变幅伸缩机构的运动平稳性,有必要对液压泵流量非线性补偿进行研究。通过实验测得液压泵压力、转速与容积效率关系的先验数据,建立映射模型,可以准确描述变转速泵在不同转速和压力下的流量非线性关系,利用映射模型对泵实时压力下的泄漏进行补偿,提高系统流量控制的精度和运动平稳性。

笔者主要研究汽车起重机变转速电液流量匹配控制系统中,液压泵流量的非线性和非线性负载扰动问题。

笔者针对液压泵泄露造成的流量非线性问题,搭建系统流量非线性数学模型,基于先验数据,构建泵的流量非线性映射模型,通过AMESim仿真软件,以汽车起重机变幅机构为研究对象,对比分析在不同转速和不同负载波动下,流量补偿前后液压泵的实际输出流量,验证所设计的流量非线性映射模型对流量非线性和非线性扰动的补偿效果。

1 电液流量匹配系统

为了降低汽车起重机传统LS系统的能量损耗,提高系统的动态响应性能,笔者提出一种基于变转速的电液流量匹配控制系统。

变转速电液流量匹配系统如图1所示。

图1 变转速电液流量匹配系统1—定量泵;2—永磁同步电机;3—溢流阀;4—减压阀;5—阀前补偿多路阀;6,7—电比例减压阀;8,9—变幅伸缩缸

系统中,控制器根据变幅手柄和伸缩手柄的开度信号,实时计算系统所需流量,并同步控制永磁同步电机转速和各联主阀的阀口开度,实现系统流量的供需匹配。

无论变幅联与伸缩联是单独动作还是复合动作,当液压泵提供流量大于工作联所需流量时,即系统处于流量不饱和状态时,工作联主阀由实际输入手柄的开度信号控制阀口开度分配流量;当液压泵提供流量小于工作联所需流量时,即系统处于流量饱和状态时,工作联主阀按抗流量饱和控制算法控制阀口开度分配流量,提升系统的操控性。

在传统的LS系统中,输入到变幅伸缩机构的流量仅由比例主阀调节,非线性影响因素少。而变转速电液流量匹配系统在阀控系统的基础上,又加上泵控系统的电机转速波动、液压泵流量非线性等因素,严重影响了系统的控制性能。

因此,笔者针对液压泵流量非线性及非线性负载扰动问题,提出一种流量非线性映射模型,改善流量控制的精度和运动平稳性。

2 非线性数学模型

2.1 永磁同步电机模型

永磁同步电机将控制器输入的电压信号转化成电机的输出转速,两者关系为:

(1)

式中:Uq—电机q轴电压,V;RS—电机绕组阻值,Ω;Lq—电机q轴电感,H;iq—电机q轴电流,A;ωm—电机输出转速,rad/s;Ke—永磁体反电动势系数,V/(rad·s-1);Te—电机扭矩,N·m;Kt—电机扭矩系数,N·m/A;TL—液压泵产生的负载扭矩,N·m;Dp—液压泵排量,m3/rad;pL—液压泵排油腔与吸油腔的压差,Pa;Jm—电机泵转动惯量,kg·m2;Bm—电机泵运动副产生的与电机输出转速ωm相关的摩擦系数。

整理式(1)得:

(2)

2.2 定量泵模型

接下来,笔者考虑泵的内、外泄漏,分析定排量液压泵流量分布特性。

定排量液压泵流量分布如图2所示。

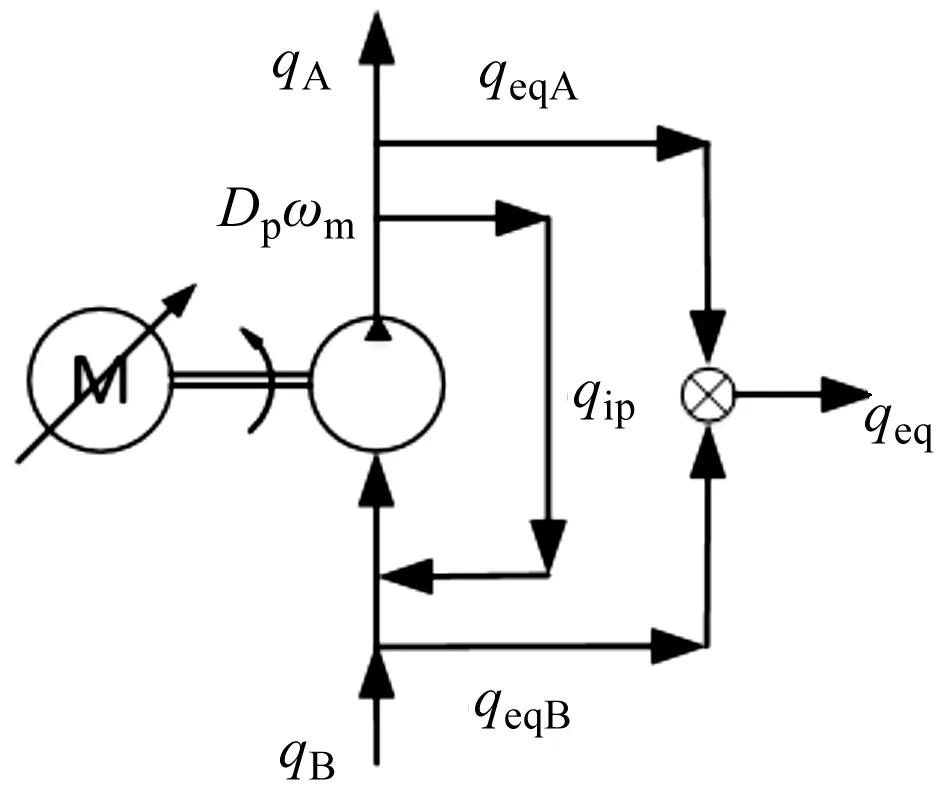
图2 定排量液压泵流量分布

定量泵输入输出的流量可表示为:

(3)

式中:qA—泵输出流量,m3/s;qB—泵吸入口流量,m3/s;Cip—泵的内泄漏系数,(m3·s-1)/Pa;Cep—泵的外泄漏系数,(m3·s-1)/Pa;pA—泵出口压力,Pa;pB—泵进口压力,近似标准大气压力,Pa。

2.3 液压缸模型

考虑液压缸内泄漏、外泄漏与油液压缩特性等因素,流入液压缸的流量为:

(4)

式中:q1—流入液压缸的流量,m3/s;A1—液压缸无杆腔有效工作面积,m2;xp—液压缸活塞杆位移,m;Ci—液压缸内泄漏系数,(m3·s-1)/Pa;p1—液压缸无杆腔压力,Pa;p2—液压缸有杆腔压力,Pa;Ce1—液压缸无杆腔外泄漏系数,(m3·s-1)/Pa;V1—液压缸无杆腔有效容积,V1=V01+A1·xp,其中:V01—液压缸无杆腔及其连接管道的初始容积,m3;βe—包含油液、液压缸缸体和连接管道的机械柔度在内的有效体积弹性模量,Pa。

流出液压缸的流量为:

(5)

式中:q2—流出液压缸的流量,m3/s;A2—液压缸有杆腔有效工作面积,m2;Ce2—液压缸有杆腔外泄漏系数,(m3·s-1)/Pa;V2—液压缸有杆腔有效容积,V2=V02+A2·xp,其中:V02—液压缸有杆腔及其连接管道的初始容积,m3。

液压缸活塞杆上的动力学平衡方程为:

(6)

式中:mt—液压缸活塞杆上总等效质量,kg;Bc—油液总粘性阻尼系数N/(m·s-1);K—负载等效弹簧刚度,N/m;Fu—系统未知的非线性负载力,N。

3 流量非线性映射模型

汽车起重机电液流量匹配系统是通过永磁同步电机和比例阀的协同控制,来实现起重机变幅伸缩机构的单独和复合动作,节能效果好。

变转速泵的输出流量容易受到泵进出口压力变化的影响,呈非线性。

笔者以汽车起重机变幅机构为研究对象,通过实验测得液压泵压力(泵进出口压力差)pA-pB、转速ωm与容积效率ηV的关系,拟合得到液压泵不同转速和不同压力下的容积效率云图,根据泵实际运行工况,经运算转换通过电机转速补偿泵的泄露流量,最终构成泵流量非线性映射模型。

液压泵压力-转速-容积效率云图如图3所示。

图3 液压泵压力-转速-容积效率云图

液压泵实际输出流量Qp可以看做两部分组成,一部分是由输入信号决定的理论流量f(Q,p),另一部分是用于补偿泄露的流量C(pA-pB,ωm,ηV),由泵流量非线性映射模型得出。

结合式(2～6),可得变转速定量泵的流量非线性模型[16-18]:

Qp=f(Q,I)+C(pA-pB,ωm,ηV)

(7)

笔者采用安装在液压泵出口的压力传感器和泵轴上的转速传感器,分别实时采集泵口压力和泵轴转速,并将采集到的压力信号和转速信号反馈至系统控制器中,控制器计算液压泵理论输出流量和实际输出流量的偏差(该偏差即为液压泵实时泄漏量),将该泄漏量转换为转速信号,通过电机转速补偿实现系统流量的精确控制。

4 系统仿真及分析

4.1 仿真模型搭建

在AMESim软件中,笔者利用HYD模块和HCD模块搭建变转速电液流量匹配控制系统仿真模型。

电液流量匹配控制系统仿真模型如图4所示。

图4 电液流量匹配控制系统仿真模型

AMESim仿真模型主要参数如表1所示。

表1 仿真参数表

4.2 流量非线性仿真

笔者对电机输出理论转速分别为1 000 r/min、1 500 r/min和2 000 r/min(流量分别为126 L/min、189 L/min和252 L/min)时,流量补偿前后液压泵的输出流量进行对比仿真分析(其中,流量补偿前的仿真模型,是将图4所示仿真模型上的泵出口压力传感器和电机转速传感器的信号断开即可)。

电机输出理论转速为1 000 r/min、1 500 r/min和2 000 r/min时,流量补偿前后液压泵压力-流量曲线分别如图(5～7)所示。

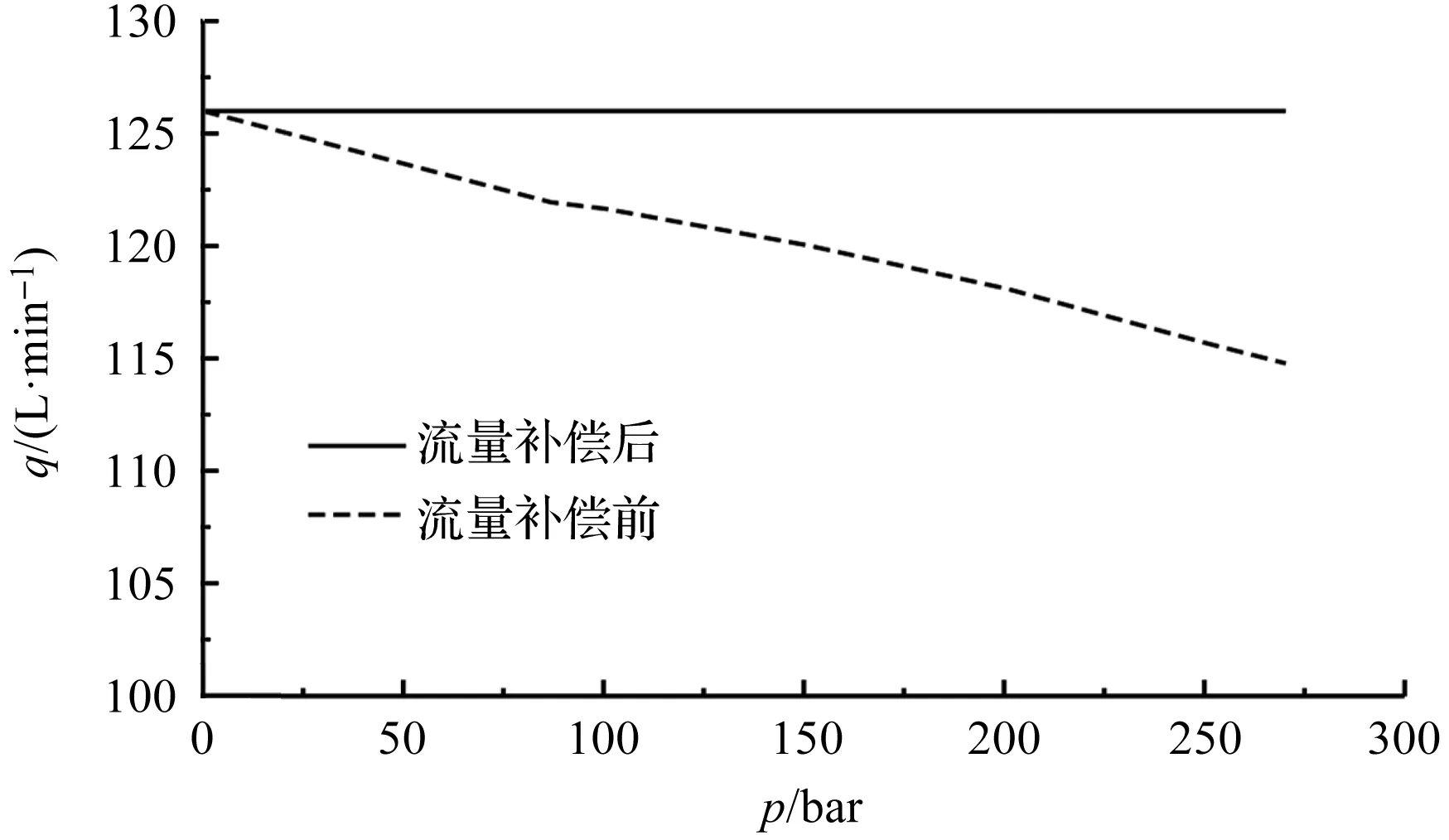
图5 理论转速1 000 r/min时补偿前后液压泵压力-流量曲线

图6 理论转速1 500 r/min时补偿前后液压泵压力-流量曲线

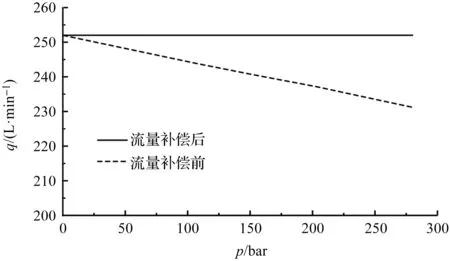
图7 理论转速2 000 r/min时补偿前后液压泵压力-流量曲线

由流量补偿前后液压泵压力-流量曲线可知:

没有加非线性补偿时,由于液压泵出口压力随变幅负载的增加而增大,液压泵的泄漏量也随之增大,导致在定转速时液压泵实际输出流量随着压力增大而减小,影响系统的运动控制性能;

加入非线性补偿后,控制器能够实时根据压力和转速信号计算液压泵的泄漏量,并根据该泄漏量对电机转速进行补偿,使得液压泵的实际输出流量匹配主阀的设定流量,不随负载压力的变化而变化,提升系统的流量控制精度。

4.3 非线性负载扰动仿真

当负载力出现波动时,带来的是液压系统油液压力的波动,压力的变化又影响液压泵的泄漏,使得液压泵输出的流量出现波动,进而带来输入到系统的流量波动,最终使得液压缸的速度出现较剧烈的波动,引起起重臂抖动的现象,影响起重臂运动的平稳性。

非线性扰动规律如图8所示。

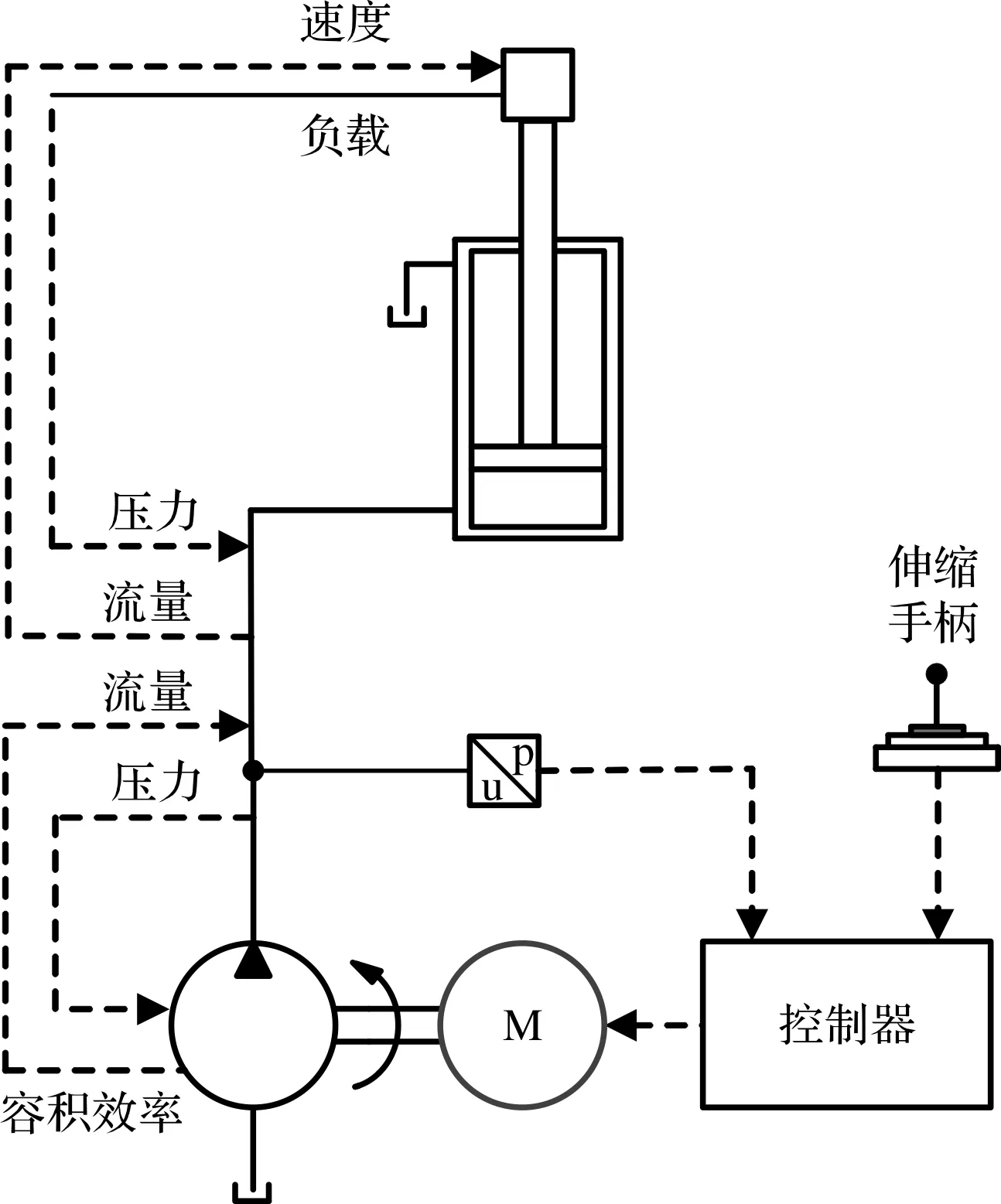
图8 非线性扰动规律

笔者根据液压泵流量非线性映射模型,实时采集系统压力的变化,计算液压泵的泄漏量,从而对电机转速进行补偿,使得输出到系统中的流量基本保持不变,液压缸的运动也不会出现剧烈的波动现象。

在流量补偿前后的仿真模型上,笔者设置电机输出理论转速为1 000 r/min,起幅初始负载300 kN,在第5 s开始负载分别产生25 kN、50 kN和75 kN这3种阶跃波动,1 s后恢复初始负载300 kN,对比仿真分析非线性负载扰动影响。

随着非线性负载力的变化,变幅缸压力也相应产生波动,波动的幅值分别大约为6.5 bar、13.1 bar和19.7 bar。

25 kN、50 kN和75 kN阶跃负载波动变幅缸压力曲线,如图9所示。

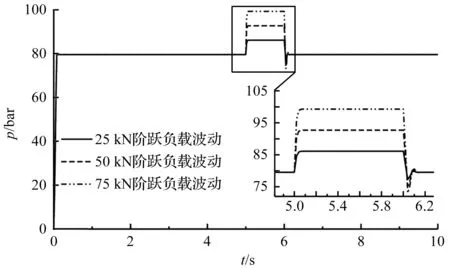
图9 不同阶跃负载波动下变幅缸压力曲线

当阶跃负载力波动分别为25 kN、50 kN和75 kN时,液压泵出口压力随之发生变化,进而影响液压泵的泄漏。根据液压泵流量非线性映射模型,电机转速随压力变化对流量进行补偿。

25 kN、50 kN和75 kN阶跃负载波动下电机转速曲线,如图10所示。

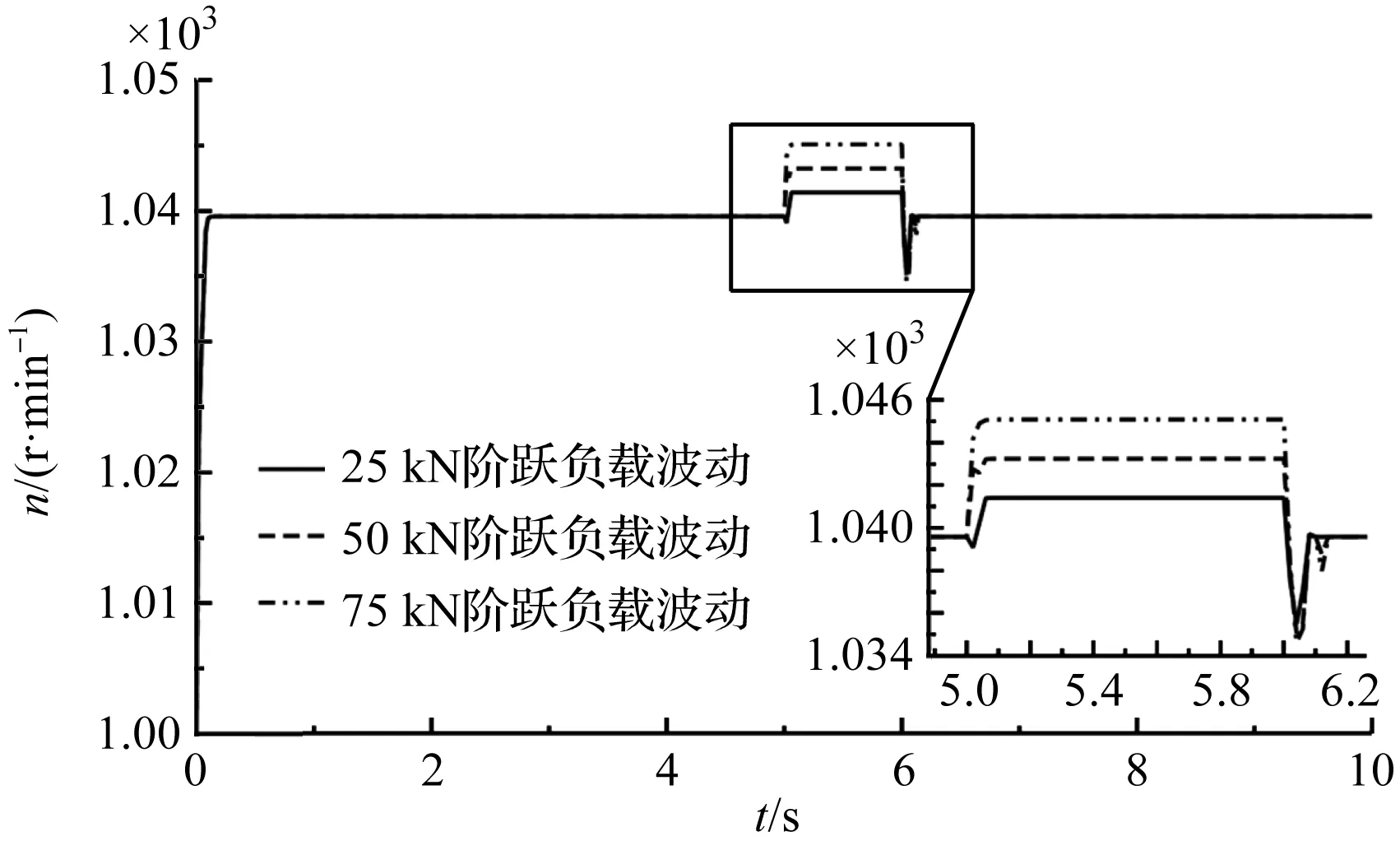
图10 不同阶跃负载波动下电机转速曲线

25 kN、50 kN和75 kN阶跃负载波动液压缸进油流量曲线分别如图(11～13)所示。

图11 25 kN阶跃负载波动下液压缸进油流量曲线

图12 50 kN阶跃负载波动下液压缸进油流量曲线

图13 75 kN阶跃负载波动下液压缸进油流量曲线

由图(11～13)可以看出:在相同输入条件下,由于流量非线性映射模型的补偿作用,泄漏补偿后的流量比泄漏补偿前的流量大3.6 L/min;

当出现25 kN阶跃负载波动时,泄漏补偿前流量波动最大幅值为6.72 L/min,泄漏补偿后流量波动最大幅值为3.22 L/min,最大波动幅值减小3.5 L/min,减小了52.1%;

当出现50 kN阶跃负载波动时,泄漏补偿前流量波动最大幅值为14.4 L/min,泄漏补偿后流量波动最大幅值为7.5 L/min,最大波动幅值减小6.9 L/min,减小了47.9%;

当出现75 kN阶跃负载波动时,泄漏补偿前流量波动最大幅值为20.9 L/min,泄漏补偿后流量波动最大幅值为11.8 L/min,最大波动幅值减小9.1 L/min,减小了43.5%。

通过对比可知:随着非线性负载扰动幅度的增大,虽然补偿效果有所减弱,但仍能起到很好的补偿效果,提升运动平稳性。

5 结束语

针对液压泵泄露造成的流量非线性问题,笔者提出了一种基于先验数据构建液压泵的流量非线性映射模型,用于研究变转速电液流量匹配控制系统液压泵流量非线性和非线性负载扰动问题。

笔者搭建了系统流量非线性数学模型,构建了泵的流量非线性映射模型,并以汽车起重机变幅机构为研究对象,对比分析了不同转速和不同负载波动下,流量补偿前后液压泵的实际输出流量,验证了流量非线性映射模型对流量非线性和非线性扰动的补偿效果。

研究结论如下:

(1)在液压泵的流量非线性映射模型的补偿作用下,系统能够实时根据压力和转速信号对电机转速进行补偿,使得液压泵的输出流量不随负载压力发生变化;

(2)采用液压泵流量非线性映射模型,当负载出现25 kN、50 kN和75 kN阶跃波动时,最大波动幅值分别减小了52.1%、47.9%和43.5%;该结果验证了液压泵的流量非线性映射模型的补偿效果。

变转速电液流量匹配控制系统存在多种非线性因素,严重影响系统的控制性能。因此,在本次研究的基础上,即在此液压泵流量非线性映射模型的基础上,笔者下一步将会对影响系统的其他非线性因素进行研究。