基于机器学习MLR模型的地下水循环井优化设计

赵思远，方 樟，周 睿，刘治国，丁小凡，马彦玲

(吉林大学新能源与环境学院，吉林 长春 130021)

随着经济的不断发展，地下水污染问题日益加剧，地下水污染修复工作成为当今环境领域的热点问题。地下水循环井(groundwater circulating well,GCW)技术自20世纪80年代开始受到广泛关注[1-2]。该技术具有修复效果好、对场地扰动小等优点[3-4]，并可以将吹脱、空气注入、气相抽提、强化生物修复和化学氧化等多种技术结合应用在井中，实现非水相液体及部分无机物的同步去除[5]。GCW运行时能够形成水平和垂直两个方向的地下水流场，穿透低渗透地层[6]，去除地下水和饱和土壤中的污染物，对于处理挥发性有机化合物(VOCs)、半挥发性有机化合物(SVOCs)、石油产品以及无机物均有良好的效果[7-8]。

GCW技术的大量研发和使用始于德国IEG公司。1980年GCW技术在欧洲首次进行了商业污染场地修复应用。20世纪90年代，该技术在欧美进行了大量的中试研究[9-10]，对地下水循环原理、GCW的性能、污染物去除机理等有了深入的认识，获得了系统设计、工艺参数等实践经验[11]。20世纪90年代后期，GCW技术已经相对成熟。目前GCW技术已有很多专利，并已市场化，且已经有很多成功的现场工程经验[3]。但目前对于GCW的研究主要集中在对污染物修复的有效性方面，而对GCW水力环流特征及结构优化设计的研究还稍显不足。

水力循环带的范围是GCW设计必不可少的考虑因素。GCW水力环流运行效果受水文地质参数、循环井结构参数和运行参数等多个因素的综合影响[12]，且在不同条件下其运行效果差异明显。GCW的运行效果往往采用影响半径(R)、捕获区范围(ZOI)等指标进行刻画[7]。目前对GCW中地下水运动特征及优化设计的研究方法主要包括室内试验、数值法和解析法。如白静等[13]通过室内试验，分析地下水初始水位、曝气量、循环井结构等参数对GCW影响半径的作用，并在二维模拟槽中进行了运行参数优化及修复试验；Elmore等[14]利用数值模拟方法预测了GCW的水力性能，分析了循环井结构参数、水文地质参数对GCW运行效果的影响，并将数值模拟的结果应用于污染场地，根据水文地质条件设置筛管位置，通过现场观测数据验证了模型预测的可行性；Philip等[15]运用解析方法预测了承压含水层中GCW运行的三维流场，分析了GCW的水力性能。

随着GCW研究的进一步深入和污染场地等数据的大量累积，可以采用机器学习(machine learning)的方法，从已有数据中学习总结，形成GCW运行效果刻画指标与各影响因素之间的函数关系，用于指导污染场地GCW的优化设计，能够在一定程度上弥补以往研究手段的局限性。机器学习是人工智能的一个分支，通过输入数据，能够自行学习，并解决具体问题[16]。利用机器学习可以通过计算机在海量数据中学习数据的规律和模式，从中挖掘出潜在的信息，广泛用于解决分类、回归、聚类等问题[17]。线性回归算法是机器学习算法的一种，是解决回归问题常用的工具，在处理大量数据和较少数据的特征时，多元线性回归(multiple linear regression，MLR)模型是寻找输出参数与输入参数之间关系最常用的模型，模型解释性强，在各领域具有广泛的适用性[18-19]。

为了确定GCW运行效果与各影响因素之间的关系，本文提出一种基于机器学习MLR模型的GCW优化设计方法。该方法首先利用有限差分法构建数值模型，并在GCW适用参数范围内，通过给定不同的数值对典型条件下GCW运行情况进行了数值模拟，从而构建数据集；然后运用MLR模型得出GCW影响半径与各影响因素表征参数之间的关系；最后以某典型试验场地为例，对循环井结构、运行参数进行了优化设计，以验证方法的有效性。

1 研究方法

本文的研究方法是：首先采用数值模拟的方法建立数值模型，构建单个GCW运行时各表征参数的数据集；然后通过机器学习线性回归算法进行训练，得出GCW各运行效果刻画指标与水文地质参数、循环井结构、运行参数之间的函数关系；最后将某试验场地的水文地质参数代入该函数关系，得出可应用于该试验场地的数学模型，从而求得GCW最优参数组合。

1. 1 地下水循环井及场地概化

典型的GCW由一个不透水的实段分隔两个筛段(抽水筛段、注水筛段)[20]。其中，抽水筛段部分从地下系统中抽取受污染的地下水，经过处理后通过同一口井的注水筛段注入含水层，从而在抽水筛段和注水筛段之间形成垂向循环流，见图1。

图1 典型的地下水循环井(GCW)运行方式示意图

1. 2 数值模型的建立

本文利用GMS软件的MODFLOW模块对GCW水力驱动下地下水流运动进行了数值模拟计算[21-22]，并在地下水流模型的基础上，利用MODPATH模块，建立GCW水力驱动下的粒子示踪模型[23-24]，分析粒子运动轨迹，刻画GCW驱动地下水环流的运行效果。在抽水筛段所在剖分单元格的4个面上各设置25个粒子作为粒子迁移的终点(见图2)，反向追踪至粒子起点，分析其在水力驱动下的运动轨迹，并通过在模型中输入不同的参数观察粒子运动轨迹，进而确定不同参数条件下GCW的运行效果变化情况。

图2 地下水循环井(GCW)粒子投放位置示意图

1. 3 地下水循环井适用条件和数据集形式

1.3.1 地下水循环井适用条件分析

GCW技术适用于饱和带为1.5～35 m、非饱和带为1.5～3 m、各向异性为3～10、渗透系数为3.0×10-4～0.30 m/d、地下水流速低(<3.0×10-4m/d)的多孔介质中，该条件下更易形成三维椭圆形流场[25-26]。

1.3.2 数据集形式

根据GCW的适用条件，通过在数值模型中给定不同的参数值并运行模型，来模拟各种条件下GCW的运行情况，并记录给定的参数及运行效果刻画指标数据，从而构建数据集。数据集包含的变量众多，本文将水文地质参数和循环井结构、运行参数作为自变量。其中，水文地质参数包括含水层厚度(M)、含水层水平渗透系数/垂向渗透系数(KH/KV)、含水层水力梯度(I)、含水层孔隙度(n)、含水层给水度(μ)；GCW结构参数包括抽注筛段总长度/含水层厚度(a/M)；GCW运行参数为抽注水量(Q)。GCW运行时周围的含水层受其影响可划分为上游捕获带、下游释放带和循环带，本次研究在充分总结了国内外已有研究成果的基础上[14]，提出了用捕集效率(Ec)、横向影响半径(RT)、纵向影响半径(RL)、捕获带上部宽度(Bt)、捕获带下部宽度(Bb)5个指标来刻画GCW的运行效果(见图3)，并将这些变量作为因变量。数据集所涵盖的介质从粉砂到粗砂，含水层厚度(M)为1～35 m不等，含水层水平渗透系数/垂直渗透系数(KH/KV)为1～15不等，抽注水量(Q)为1～300 m3/d不等，变量数值分布均匀、广泛，所涵盖的情形众多(共717套)，具有一定的代表性(见图4)。

图3 地下水循环井(GCW)运行效果刻画指标示意图

1. 4 回归模型的构建与评估

1.4.1 回归模型构建

本次回归模型的构建采用Python语言中的Scikit-learn程序包利用线性回归算法训练模型。Python语言是一种解释性、交互式、面向对象的跨平台语言，语法简洁清晰，代码开发效率高[27]，Scikit-learn是Python语言中的一个程序包，集成了各种最先进的机器学习算法，可用于解决中等规模的监督和无监督问题[28-29]。通过已有数据集训练获取各个因变量与自变量之间的关系，这属于典型的回归问题[30]。

图4 数据集各参数的分布统计

本文将数据集划分为20%的测试集和80%训练集，训练集用于模型训练，测试集用于模型评估。采用机器学习线性回归算法进行模型训练，假设线性回归模型试图学得[31]:

f(x)=wTxi

(1)

可用最小二乘法对w进行估计，损失函数J(w)为

J(w)=[f(x1)-y1]2+[f(x2)-y2]2+…+[f(xm)-ym]2

(2)

式中：x，y，w可以理解为矩阵；m为训练集数据个数。

若要求出最佳的拟合方程，则要求出使J(w)达到最小时的w，即:

w=(xTx)-1xTy

(3)

通过对数据集采用Python语言中Scikit-learn程序包的Linear regression算法进行训练，可得到表示各因变量与自变量关系的5个数学模型。

1.4.2 回归模型评估

本文采用决定系数R2对建立的线性回归模型进行评估。R2表示自变量对因变量的解释程度，R2值越接近于1，表示线性回归模型的拟合程度越好。R2的计算公式如下：

(4)

2 试验场地地下水循环井参数优化设计

本次GCW结构优化设计的试验场地为陕西省某场地。该地区属暖温带大陆性季风气候，年平均气温为13℃，多年平均降水量为701 mm，降雨主要集中在每年的7—9月份。根据地下水水位监测及抽水试验结果，该场地地下水流向大致由西北向东南，浅层地下水受季节变化而升降，场地附近地下水水力梯度为0.9‰。本次研究的目标层位为第四系孔隙潜水含水层，岩性主要为粗砂、中细砂混卵石填充，其上为粉质黏土，下部为致密的粉质黏土隔水层。该潜水含水层垂向渗透系数(KV)为6.67 m/d，含水层水平渗透系数/垂直渗透系数(KH/KV)为3，含水层孔隙度(n)为0.30，含水层给水度(μ)为0.20，含水层厚度(M)为7.5 m，抽注水量(Q)为150～300 m3/d，富水性良好。

根据上述资料，该场地水文地质参数即含水层厚度(M)、含水层水平渗透系数/垂向渗透系数(KH/KV)、含水层垂向渗透系数(KV)、含水层水力梯度(I)、含水层孔隙度(n)、含水层给水度(μ)为已知，优化设计变量为GCW运行参数即抽注水量(Q)和GCW结构参数即抽注筛段总长度/含水层厚度(a/M)，将试验场地的水文地质参数代入通过机器学习训练后的各数学模型，得到适用于该试验场地的数学模型，再根据多元函数微分学，求得各数学模型的最值点，即为针对各种GCW运行效果刻画指标的优化方案。

3 研究结果与讨论

本文利用20%测试集对机器学习训练后得到的试验场地各模型进行测试，各模型的预测结果如图5所示，利用决定系数R2对各模型的拟合程度进行评估，其评估结果见表1。

本文利用训练后的模型构建的试验场地数学模型如下：

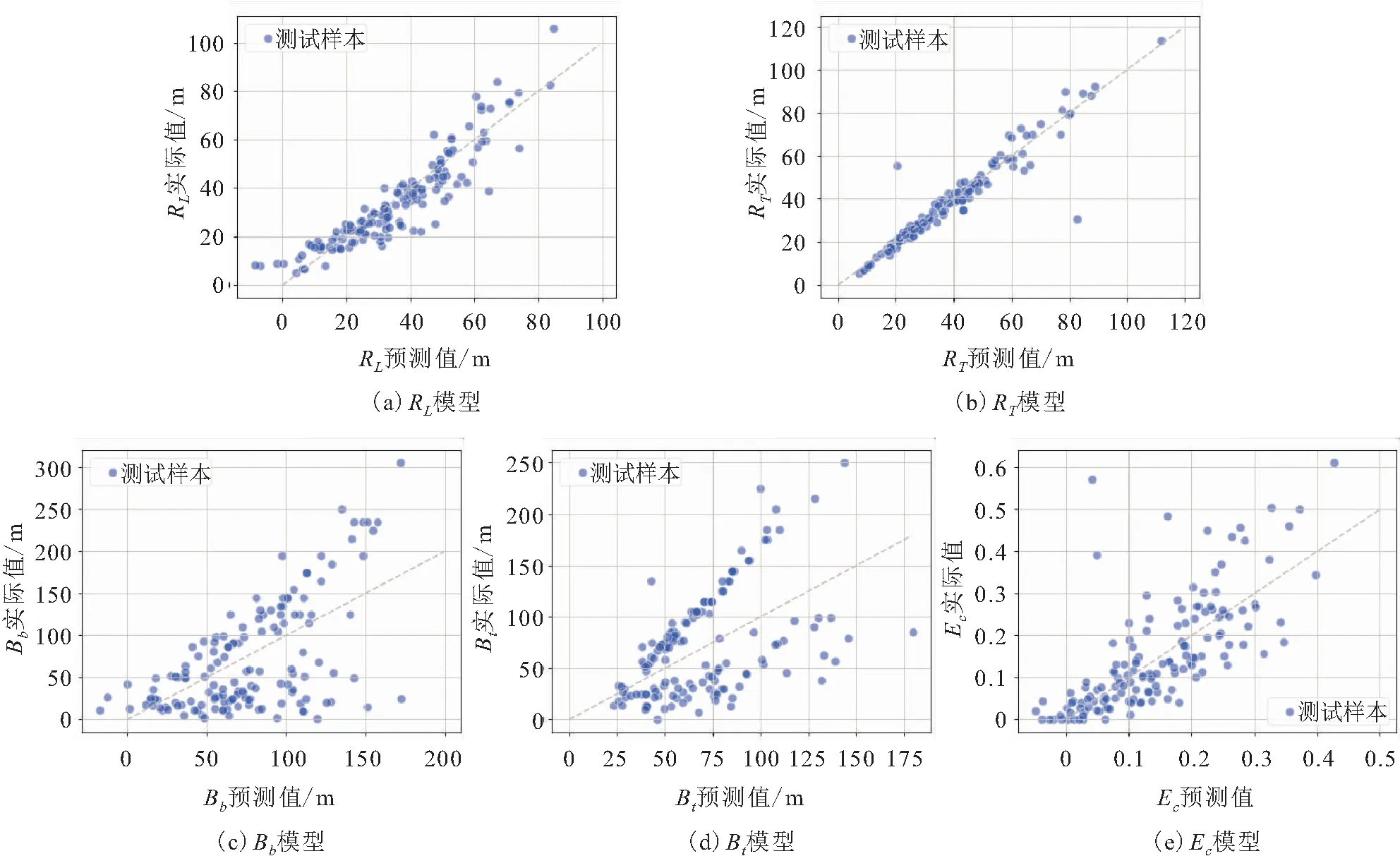
图5 试验场地各数学模型预测值与实际值对比

表1 试验场地各数学模型的评估结果

RL=0.145 5Q-3.29×10-4Q2+34.729(a/M)-26.029(a/M)2-15.732

(5)

RT=0.151Q-0.000 34Q2+36.049(a/M)-27.018 1(a/M)2-14.51

(6)

Bb=0.632Q-0.001 445Q2+68.876(a/M)-83.488(a/M)2-39.624

(7)

Bt=0.227Q-0.000 512Q2+54.067(a/M)-40.522(a/M)2-9.316

(8)

Ec=-3.6×10-4Q+8.3×10-7Q2-0.04(a/M)+0.048(a/M)2+0.36

(9)

试验场地各数学模型图像，见图6。以RL模型为例求其偏导数，其计算公式如下：

(10)

当RL对Q和a/M的一阶偏导数等于0，即Q=221.125 m3/d、a/M=0.667时模型可能取极值，又A<0、AC-B2>0，故Q=221.125 m3/d、a/M=0.667即为该模型的最优解。同理，可求得其余各模型的最优解，即为针对各种GCW运行效果刻画指标的优化方案和预期可以达到的最佳效果，见表2。对于通过机器学习线性回归算法训练获得的多个模型，图5展示出了各模型对于纵向影响半径RL、横向影响半径RT、捕获带下部宽度Bb、捕获带上部宽度Bt、捕集效率Ec的预测结果，可见RL、RT模型的散点在y=x目标线附近的分布较为密集，说明对于RL、RT两项指标模型预测的整体精度更高，其余模型的预测精度较低。此外，由表1可知，RL、RT模型的决定系数R2为0.82和0.90，相对于Bb、Bt、Ec模型R2值更接近于1，说明RL、RT模型的拟合程度、泛化能力较好，而Bb、Bt、Ec模型的拟合程度、泛化能力相对较差，其主要原因分析如下：

图6 试验场地各数学模型的图像

表2 试验场地各数学模型的最优解

(1) 因变量RL、RT与自变量之间可能存在某种程度的线性关系，线性回归算法对于拟合此类数据更加适用。

(2)RL、RT模型的复杂程度适中，未出现欠拟合和过拟合的现象，在测试集中有相对良好的表现。

(3) 通过线性回归算法训练得到的Bb、Bt、Ec模型结构较为简单，而因变量Bb、Bt、Ec与自变量之间的关系较为复杂，线性回归算法对于复杂映射关系的拟合能力有限，故出现欠拟合的情况。

(4) 由于数据集样本数量有限，不足以体现因变量与自变量之间的复杂关系；同时，通过数值模拟构建的数据集存在一定的测量误差，对于小样本数据的影响较大，导致训练得到的模型拟合精度较低，而用有限的测试集对模型进行测试，测试结果具有不稳定性。

根据以上情况，通过MLR模型训练得到的RL、RT预测模型更为可靠，根据RL、RT模型求得的最优解为Q=221.125 m3/d、a/M=0.667(见表2)，可作为试验场地优化GCW影响半径的优化设计方案。

在此次优化设计之前，根据试验场地的水文地质条件建立了地下水流模型、溶质运移模型并进行了若干次数值模拟，观察在不同井流量和筛管长度下GCW影响半径的变化情况，初步得出Q=150 m3/d、a/M=0.40的GCW设计方案，对比优化前后的参数并运行数值模型，可以发现井流量和筛管长度以及GCW影响半径发生了一定的变化(见表3)，可见经过优化后纵向影响半径RL从15.77 m提升到16.9 m，提升率为7.2%，横向影响半径RT从18.02 m提升到19.65 m，提升率为9%，优化后RL、RT指标值均大于优化前的数值，体现了基于机器学习MLR模型对试验场地GCW进行优化设计的有效性。

表3 试验场地地下水循环井(GCW)优化前后参数值的对比

4 结 论

地下水循环井(GCW)运行效果对污染场地修复至关重要。本文以数值模拟获取结果为数据集，利用机器学习多元线性回归(MLR)模型得出GCW影响半径与各参数之间的数学模型，并根据特定试验场地，初步确定了对于GCW影响半径的优化设计方案，可以为GCW的优化设计提供参考，能够在一定程度上减少GCW布设后的调试时间，并降低运行成本，具有实际意义。

本文针对陕西省某试验场地提出了一套GCW优化设计方案，该方案由试验场地数学模型得出，若改变为其他场地，其数学模型与此模型只有常数项不同，最值点相同，所以其他场地在流量可以达到优化方案的条件下，也可使用此优化方案。

将机器学习的方法运用到GCW优化设计是一种新的尝试，同时数值模拟作为一种新的获取数据的方法，与传统的场地试验不同，有着易操作、周期短、成本低等特点，可获取大量数据，可为机器学习创造大量数据集，将数值模拟与机器学习结合也展现出了一定的优势。本次研究的数据集根据现有全国各典型水文地质条件创建，对于特殊水文地质条件下的数据创建略显不足，若后期有更多的试验场地，可根据这些试验场地的水文地质条件模拟数据，并加入到数据集当中，使机器学习结果具有更高的可靠性。