探究事件相关脑电/脑磁信号中的神经表征模式：基于分类解码和表征相似性分析的方法*

陈新文 李鸿杰 丁玉珑

(华南师范大学脑认知与教育科学教育部重点实验室;华南师范大学心理学院;华南师范大学心理应用研究中心;广东省心理健康与认知科学重点实验室,广州 510631)

1 前言

得益于计算机硬件和算法的发展,越来越多行之有效的技术方法被用于神经影像数据分析。自机器学习中的分类算法(即基于分类的解码,classification-based decoding,简称解码分析)开创性地引入到功能性磁共振成像(functional magnetic resonance imaging,简称fMRI)数据分析之中,人们能够更好地识别与分类特定大脑认知加工活动对应的神经表征(Cox &Savoy,2003;Kamitani &Tong,2005;Norman et al.,2006)。除了解码分析外,一种称作表征相似性分析(representation similarity analysis,简称RSA)的方法也被广泛应用于fMRI研究中,它可以评估不同神经表征之间的相似性关系,具有跨任务、跨模态、跨群体等优点(Kriegeskorte,Mur,&Bandettini,2008)。两种新方法的引入,让研究者在大脑的空间结构上对神经表征信息的理解更加深刻。

解码分析与RSA 近年来也被逐渐用于脑电(electroencephalography,简称 EEG) 和脑磁(magnetoencephalography,简称MEG)数据分析中(Carlson et al.,2011,2013;Cichy et al.,2014,2016;Cichy,Pantazis,&Oliva,2016;Cichy,Kriegeskorte,et al.,2017;Cichy,Khosla,et al.,2017;Wardle et al.,2016;Teichmann et al.,2018;Dobs et al.,2019;Giari et al.,2020;Kong et al.,2020;Xie et al.,2020)。fMRI 由于其高空间分辨率,相应的研究更多关注的是大脑空间结构上的认知加工机制;与fMRI 不同的是,EEG/MEG 高时间分辨率的特点使得相应的研究更适合从时间进程上探索大脑的认知加工机制。将解码分析与RSA 引入EEG/MEG研究中,既可以在一定程度上克服传统EEG/MEG数据分析中存在的不足,还能够从不同的角度去解释大脑对神经表征信息的动态编码情况。

本文将从解码分析和RSA 这两种新方法与传统EEG/MEG 分析的对比展开介绍,简要阐明两种新方法的基本原理与优势;之后将对上述方法的具体实现进行阐述,并通过梳理前人采用解码分析和RSA 开展的EEG/MEG 研究,讨论两种技术在认知神经科学领域的实际应用场景;对于这两种技术在未来的EEG/MEG 研究中可能的应用方向,在文末提出了一些我们的见解。

2 原理总论

随着认知神经科学研究的不断深入,传统的EEG 和MEG 分析方法已无法满足研究人员的全部需求,人们需要寻找更加精细的方法来识别与分析大脑活动模式。EEG 和MEG 由于高时间分辨率、非侵入式等特点被广泛应用于各类大脑认知加工的研究,并形成了一套成熟的数据处理流程。现有的事件相关EEG/MEG 研究需要计算每个被试迭加平均后的事件相关电位(event-related potentials,简称ERPs)或事件相关磁场(event-related magnetic fields,简称ERMFs),并在此基础上求出不同条件之间的差异波或者地形图,之后再进行群体水平上的统计分析。根据不同时刻点的ERPs/ERMFs 特征值,可以随时间进程绘制振幅和地形图的变化情况来进行神经表征时空模式分析(Ding et al.,2014;Qu et al.,2014,2017)。但不论是迭加平均后的ERPs/ERMFs 还是经过计算得到的差异波和地形图均具有极性,为了尽可能地使潜在的效应更加明显,传统的EEG/MEG 研究要求所有被试在研究者关注的时间进程上,诱发出的ERPs/ERMFs振幅大小和方向以及地形图分布和极性等均要在不同被试之间具有较高的一致性,在一致性较差的情况下对不同被试的神经响应水平进行平均后,得到的结果可能难以做出合理的解释(图1)。

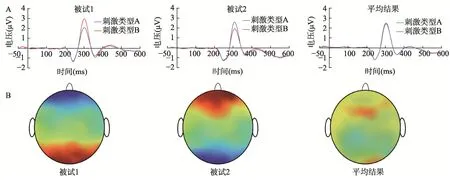
图1 传统ERP 研究示例。(A)假设在某一特定通道上对不同条件诱发的ERPs 成分进行分析,能够观测到不同的被试在不同刺激条件间均存在明显的ERPs 差异,这提示了两种刺激可能具有不同的神经表征,使得每名被试都能区分这两种刺激。由于受到个体差异的影响,不同被试在刺激条件间的ERPs 差异方向可能是不一致的,这将导致在对所有被试的数据进行组平均处理后,可能会使得研究者不能从组平均ERPs 上区分两种刺激,从而做出两种刺激具有相似神经表征的错误推论。(B)由于被试间存在着个体差异,假设对于相同的刺激条件,在某一时刻下不同的被试均能诱发出较为明显的大脑活动模式,但在不同的通道上激活水平的极性不同,可能使得不同被试的地形图映射情况差别很大,导致人们同样可能对所有被试进行组平均后得到的结果做出错误的解释。

相比于传统的EEG/MEG 分析方法,解码分析和RSA 并不需要不同被试之间的ERPs/ERMFs振幅等信息具有较高的一致性,它们更多地要求事件相关的EEG/MEG 信号在每个被试内部具有较高的一致性(即存在相对稳定的加工机制)。以不同的刺激类型为例,解码分析和RSA 的基本假设是：当大脑对特定刺激信息进行了有效编码时都会产生对应的活动模式,如图2A 所示,每个试次记录到的大脑活动模式可以投射到由所有通道(记录EEG 信号的电极、MEG 信号的磁力计和平面梯度计)共同构成的神经表征空间中(为便于展示此处将其简化为三个通道构成的三维空间),并得到其对应的响应向量(即神经表征空间中的点),该响应向量的特征坐标由各个通道包含的幅值信息转换而来(Haxby et al.,2014)。每种类型的刺激信息在神经表征空间中的分布是不同的,同一刺激条件下的大脑活动模式将被投射到神经表征空间中的某个特定区域,具体表现为相同类型的刺激信息在空间分布上更加集中,且集中于某个区域内所有的响应向量都表征了同一类信息,例如刺激类型、认知状态等(Cox &Savoy,2003;Kamitani&Tong,2005;Grootswagers et al.,2017;Hebart &Baker,2018;Carlson et al.,2019)。而当大脑未对特定刺激信息进行编码时,如图2B 所示,其对应的响应向量在神经表征空间上的分布则是随机不可分的。

当在被试内部不同刺激条件对应的神经表征之间在关注的时间进程上存在着稳定的差异(本文称之为绝对差异)时,解码分析可以在神经表征空间中按照一定的规则找到一个能将不同类型响应向量分离开的边界(即图2C 中所示的决策边界,decision boundary),使得各种刺激类型信息所对应的大脑活动模式可以最优地区分开,从而实现对个体不同的认知状态进行分离(Haxby et al.,2014;Grootswagers et al.,2017;Kriegeskorte &Diedrichsen,2019;Weaverdyck et al.,2020)。解码正确率是衡量决策边界区分绝对差异的效果的指标,如果得到的解码正确率越高,理论上该决策边界就越能够区分不同的认知状态。无论不同被试诱发出的ERPs/ERMFs 振幅大小和方向、地形图分布情况是否一致,我们都可以借助解码分析来考察每名被试区分不同刺激条件的神经表征绝对差异(由解码正确率表示);将不同被试的解码正确率进行平均和统计检验分析,以说明不同刺激条件之间确实存在着差异(图3)。

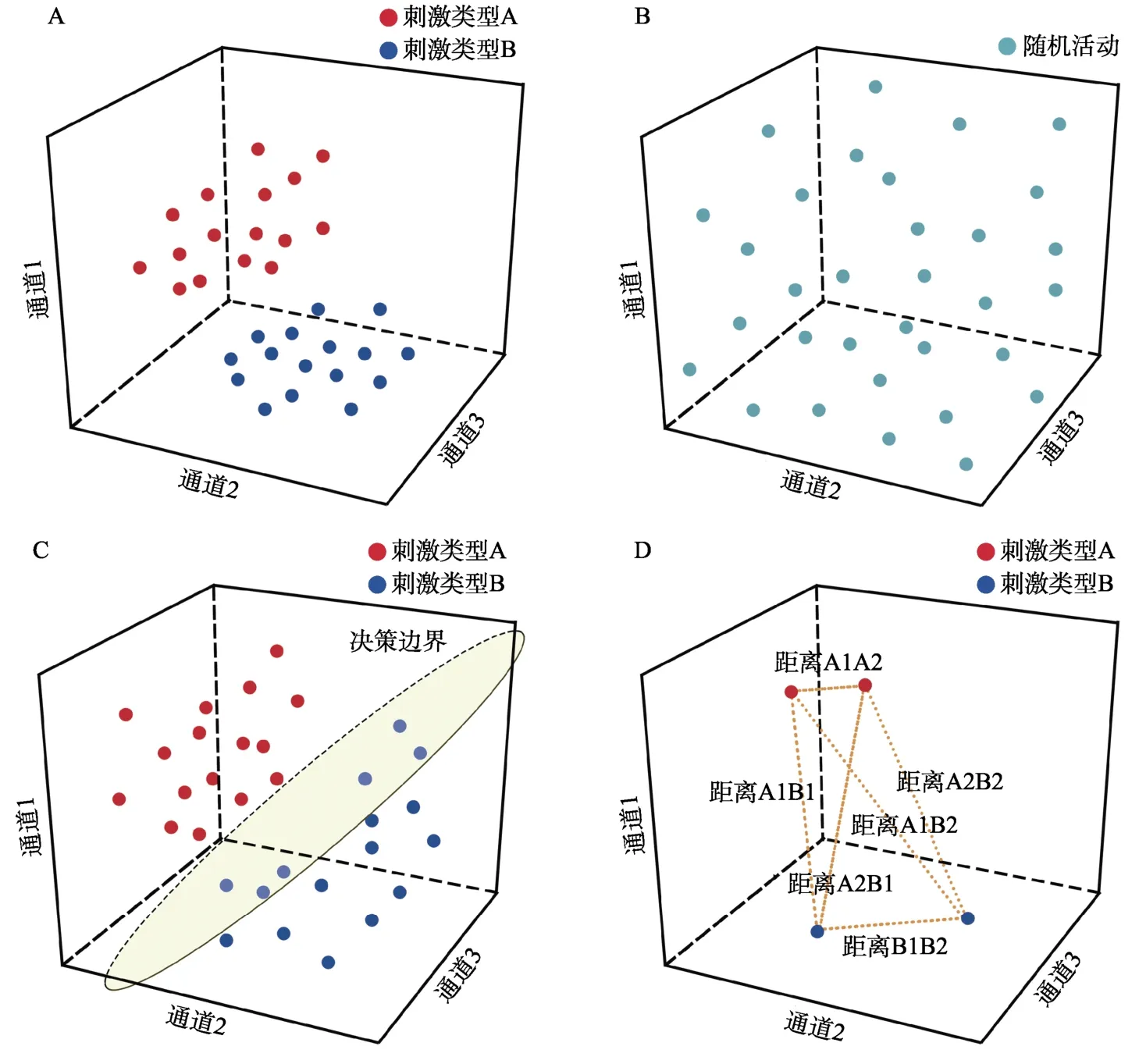
图2 以不同的刺激类型为例,(A)不同刺激信息的神经表征不同,具体在神经表征空间中会表现出同类刺激信息相聚、异类刺激信息相离的特点。(B)当大脑未对特定刺激信息进行编码的情况下,神经表征将处于随机不可分的状态。(C)解码分析可以使用决策边界对不同类型的刺激进行区分。(D)RSA 通过计算不同刺激之间的距离来说明它们之间的相似程度。

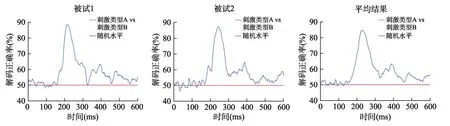
图3 以基于时域ERP 信号进行的解码分析(可以对特定时间点的单个通道或多个通道数据进行解码)为例,在每个时间点上对ERPs/ERMFs 数据进行解码,能够得到一条随着时间变化的解码正确率曲线,从而可以在时间进程上探究神经表征信息的动态编码情况。由于解码分析只关注不同的刺激条件之间是否存在着差异,而不关心这个差异的振幅极性和地形分布等具体信息,相比于图1A 的情况,此处不仅保留了每名被试对不同刺激条件的区分情况,且他们在时程上的一致性可以在平均结果中保留。

不同于解码分析寻找能够最优分离各种类型神经表征的决策边界的思路,RSA 致力于衡量不同神经表征之间的差异大小。由于同一类别的信息彼此之间的相似程度更高,在神经表征空间中表现为对应的响应向量间的距离更近,不同刺激类型的信息则由于相似程度低而表现为响应向量间的距离更远,所以RSA 可以根据每个响应向量在神经表征空间内的特征坐标来计算响应向量间的成对距离,使得不同刺激条件间神经表征的差异情况可以用对应的响应向量间距离来进行衡量(图 2D,Kriegeskorte,Mur,&Bandettini,2008;Kriegeskorte &Kievit,2013;Haxby et al.,2014;Popal et al.,2019;Weaverdyck et al.,2020)。这种根据不同脑活动量化得到的标准化差异被RSA 记录在表征差异矩阵(representational dissimilarity matrix,简称RDM)中,它反映了由不同刺激条件诱发的大脑活动模式间相似程度。当不同刺激条件的神经表征之间存在差异且这种差异稳定存在于被试内部时,此时RSA 只关心在个体水平上不同刺激诱发的脑活动是否有差异、差异程度有多大,而不关心脑活动之间的差异体现在哪些具体测量特征值上(如ERPs/ERMFs 振幅大小和方向、地形图分布情况等)。对于一组刺激而言,它们的具体测量特征值在不同被试之间可能会有很大的不同,但是当每个被试内部对这组刺激内不同刺激条件的加工存在着稳定的规律时,那么根据不同被试的EEG/MEG 活动计算得到的RDM (反映了刺激之间的绝对差异程度)有可能是相似的(如图4A 被试1、被试2 的神经RDM 所示)。此外,研究者还可以基于研究目的对不同来源和形式的数据进行量化(如图4A 分别根据行为表现和类别属性构建的行为RDM、概念RDM),并与根据EEG/MEG数据构建的逐时间点神经RDMs 进行比较,进而阐明不同类型的数据能够在哪些时程上提供一致性信息,以在不同层面反映刺激条件之间的差异(图 4B,Kriegeskorte,Mur,&Bandettini,2008;Kriegeskorte &Kievit,2013;Carlson et al.,2013;Cichy et al.,2014;Cichy,Kriegeskorte,et al.,2017;Redcay &Carlson,2015;Grootswagers et al.,2019)。

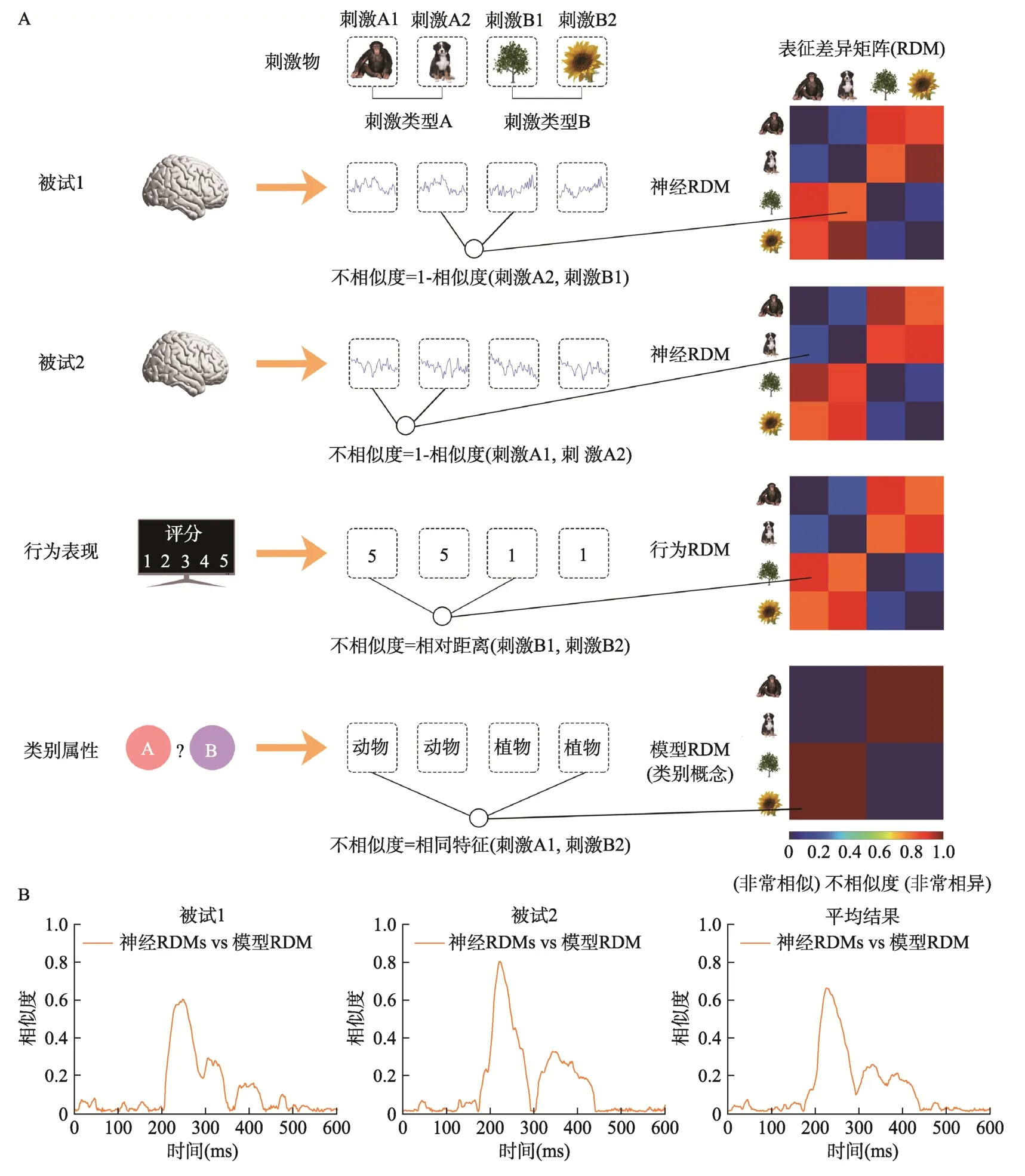
图4 RSA 方法示意图。(A)根据不同个体的神经活动、行为表现、类别属性等来对不同刺激条件之间的差异进行量化,得到的不相似度可以记录在RDM 中(此处神经RDM 的数据来源为某时间点的EEG 数据,不相似度以1-相似度(刺激M,刺激N) 来计算;行为RDM 的数据来源为行为评分,不相似度以相对距离(刺激M,刺激N)来计算;具体算法以及其它评估方式见4.2.1 节)。由于个体差异的存在,对于一组刺激以及这组刺激内不同刺激条件之间的差异,在不同被试的神经活动和行为表现上可能是不一样的;如果被试内部对不同刺激条件的加工存在稳定的规律,那么通过计算得到的RDM 在个体之间可能是类似的。(B)对于EEG/MEG 数据,可以在每个时间点上计算不同刺激条件之间的不相似度并构建对应的神经RDM,再分别与其它来源的RDM 进行比较得到相似度曲线。例如,本图显示在刺激呈现约200 ms 后出现了区分动植物类别概念的神经表征,这种分类机制在不同个体之间是一致的(尽管具体的神经表征活动模式在不同被试间可能存在较大差异)。将构建的模型RDM 与逐时间点构建的神经RDMs 进行比较,可以在一定程度上说明根据理论假设构建的模型能够在什么时程上对不同刺激类型之间的差异做出解释。

在ERPs/ERMFs 研究中,解码分析和RSA 不仅可以在时间进程上揭示个体间一致的加工机制,并且当个体间存在显著差异、但是个体内存在稳定的加工机制时,还能对具体的神经表征模式进行探索,用于识别个体的“脑指纹”。将这两种方法引入EEG/MEG 研究,可以弥补传统分析方法只关注群体水平ERPs/ERMFs 结果的不足,还能根据每个被试独有的大脑活动模式,给出个体水平上的统计分析结果,帮助人们在个体水平上理解信息编码加工的时程。

3 基于分类的解码

3.1 基本概述

解码分析起源于机器学习中的分类算法,它主要根据从样本数据中提取的特征(能够反映样本数据在某些方面的属性。ERPs/ERMFs 研究主要关注如时间-振幅、时间-通道、时间-频率-功率等特征)来训练能够区分不同类别(样本数据所属的种类,如刺激类型、认知状态等)的分类模型。在认知神经科学领域,人们可以使用与特定事件相关的 EEG/MEG 数据来训练和测试分类器(classifier),以寻找不同心智活动下的神经表征差异,从而将特定事件所对应的大脑活动信号进行区分(Pereira et al.,2009;Haxby et al.,2014;Haynes,2015;Contini et al.,2017)。以采用EEG/MEG 技术开展的一个视觉研究举例,解码分析的流程大致如图5 所示：该研究拟探究人们在识别动物刺激和植物刺激时的神经信号差异,在向被试呈现不同类型的视觉刺激并记录EEG/MEG 后(图5A),对每名被试的数据进行单独处理。首先进行数据预处理以提高解码分析的效果,再将预处理好的数据分为训练集和测试集并分别打上标签(例如试次2 和试次3 都是动物,编码为0;试次1 和试次4 都是植物,编码为1)形成训练集和测试集;然后将训练集用于训练分类器以构建分类模型(不同通道下每个试次的神经信号为预测变量,打上的标签为结果变量);最后用测试集来检验分类模型的性能,即计算模型预测标签和实际标签的差异,也就是解码正确率(图5B)。如果解码正确率高于随机水平(chance level,本研究中的随机水平为50%),说明它确实能够区分不同的大脑认知状态,因为分类器能够从训练集中学习到不同的类别与其特征之间的关系,并将这种关系推广到训练样本以外的独立数据中。对于每名被试,可以在每个时间点都分别进行上述的解码分析并得到一个解码正确率,进而绘制解码正确率随时间变化的曲线(图3);对多名被试的解码正确率曲线进行组平均分析和统计检验,能够考察不同实验条件间的神经表征差异何时达到显著,从而揭示人类大脑进行分类加工的时间进程。

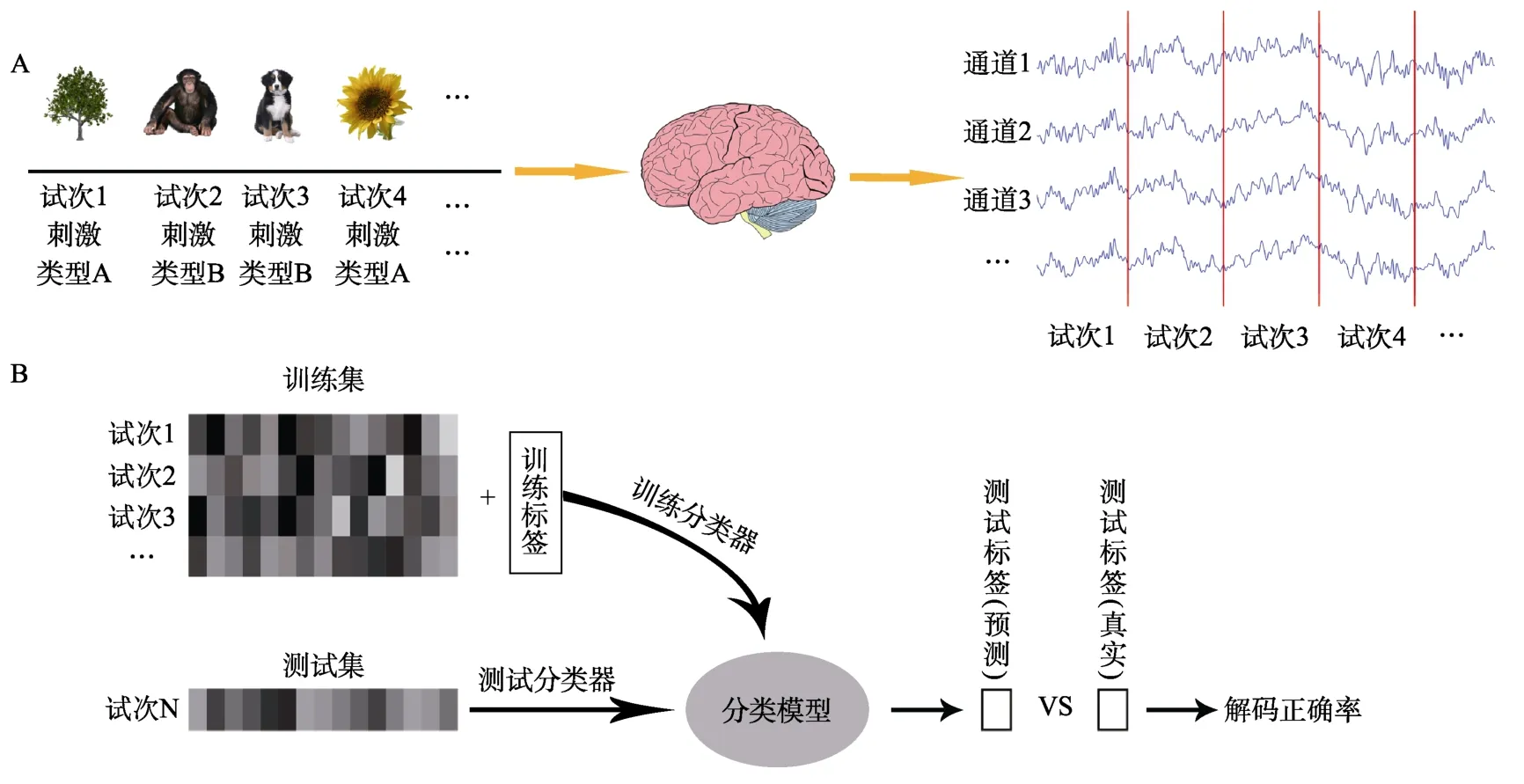
图5 解码分析流程示意图。(A)采用标准的EEG/MEG 记录方法对呈现不同类型刺激信息时被试的大脑活动信号进行采集。由于每种类型的刺激都与一种特定的大脑活动模式有关,因此可以寻找大脑与不同刺激条件之间的神经相关性。(B)解码分析的基本模型。将已有数据划分为训练集和测试集(其中色块表示用于解码分析的特征信息),使用已标记训练标签的数据来训练分类器,并使用测试集对训练好的分类器进行测试;通过计算分类模型预测的结果和真实结果之间的差异,便可以得到用于评估分类性能的解码正确率。

3.2 具体算法及实现

3.2.1 数据预处理

与传统ERPs/ERMFs 分析相似,解码分析的预处理阶段也需要使用滤波、眼动校正、伪迹排除、数据分段、重参考等方式来处理原始信号(详见Luck,2014),以尽可能地减少伪迹和噪声带来的影响。在预处理阶段,根据关注的特征类型对信号处理的操作有所不同。例如,关注特定的时域ERP 成分时需要将提取后的ERPs/ERMFs 振幅信息作为后续解码的输入,通常采用截止频率30～40 Hz 的低通数字滤波去除高频噪音(低频噪音一般是在EEG 记录时通过高通模拟滤波来去除,截止频率通常设为0.01～0.1 Hz);关注某个频段的神经震荡活动时,可以采取希尔伯特变换或小波变换的方式提取固定频段的能量信号(例如,8～13 Hz 的alpha 能量)作为后续解码的输入(Bae&Luck,2018;Xie et al.,2020)。受到通道数量、采样率、关注的特征类型等诸多因素的影响,有时为了防止输入分类器的特征数量过多而导致过拟合(over fitting)的情况发生(de Martino et al.,2008;Misaki et al.,2010;Lemm et al.,2011;Weaverdyck et al.,2020),需要对EEG/MEG 数据进行降维处理以减少数据中的冗余信息。常用的数据降维方法有主成分分析(principle component analysis)、独立成分分析(independent component analysis)和方差分析(analysis of variance)等(Pereira et al.,2009;Lemm et al.,2011;Carlson et al.,2011,2013;Charles et al.,2014;Isik et al.,2014;Sankaran et al.,2018;Dobs et al.,2019)。为了减少解码的耗时,在解码之前可以通过将时间窗内多个时间点的数据平均来对数据进行降采样(downsampling)处理,该操作会增加数据的信噪比,一定程度上能够提升解码性能,同时由于数据降到较低的采样率,使得用于训练和测试分类器的时间点数量减少,这将大幅减少信号解码的耗时,对于数据分析来说是有利的(Carlson et al.,2011,2013;Kaiser,Azzalini,&Peelen,2016;Kaiser,Oosterhof,&Peelen,2016;Giari et al.,2020)。此外,在解码分析前随机选取相同刺激条件下的部分试次进行信号平均来提高用于解码数据的信噪比,可以适当提高解码性能,并且在一定范围内,随着用于信号平均的试次数增加,其解码正确率的也会有一定的提升(Isik et al.,2014;Redcay &Carlson,2015;Grootswagers et al.,2017;Bae &Luck,2018,2019a,2019b;Collins et al.,2018)。

在预处理阶段,如果ERPs/ERMFs 在试次之间显示出较大的变异性,导致数据处于一个较大的取值范围时,则要对数据进行归一化(normalization)处理(Correia et al.,2015;Guggenmos et al.,2018;Tuckute et al.,2019;Kong et al.,2020)。归一化不仅能够避免不同数据间由于取值范围的差异所造成的影响,提高解码精度,还能适当降低训练分类器的时间成本,从而提高计算效率。常用的归一化方法有最小最大值法(min-max;Croce et al.,2018;Güven et al.,2020)和z分数法(z-score;Isik et al.,2014;Sato et al.,2018;Tuckute et al.,2019;Barchiesi et al.,2020)。

3.2.2 数据划分

在训练分类器之前,需要将预处理之后的ERPs/ERMFs 数据划分为训练集和测试集,用于训练分类器并测试其泛化性能(训练得到的分类模型对新样本数据的适应能力)。受到实际样本数量的限制,为了尽可能的对数据进行利用,提高分类器的性能,需要引入交叉验证(cross validation)的方法。最广泛使用的是k 折(k-folds)交叉验证,该过程包括了彼此相互独立的k 次迭代运算(即k次训练和测试)：首先需要将数据集等比例划分成k 个试次数相等的子集,在每次迭代过程中依次取出划分后的1 个子集作为测试集,用来对训练后的分类器性能做出评估,同时将剩下的k-1 个子集作为训练集用于训练分类器;最后将k 次迭代后得到的正确率进行平均(Pereira et al.,2009;Lemm et al.,2011;Grootswagers et al.,2017;Weaverdyck et al.,2020)。当k 折交叉验证的迭代运算次数k 等于样本量n 时,是k 折交叉验证的一种特殊形式,也称为留一法(leave-one-out)交叉验证：每次抽出一个样本作为测试集,并将剩余的n-1 个样本用来训练分类器;将该过程不断重复,直到每个样本都被作为了测试集,此时会得到n个解码正确率,它们的平均结果则作为衡量模型性能的指标。留一法对样本的利用率最高,但同时该方法会非常耗时,一般更适用于小样本的情况(Pereira et al.,2009;Lemm et al.,2011;Carlson et al.,2013;Tucciarelli et al.,2015;Grootswagers et al.,2017,2019;Robinson et al.,2019)。

应当注意的是,在一个完整的训练-测试流程中,训练和测试的数据需要保持相互独立,如果对来自相同刺激条件的某个试次同时执行训练和测试两个步骤,容易造成分类器过拟合的情况,进而对其性能造成影响(Fahrenfort et al.,2018)。另外,还需要尽量保持各个条件之间样本数量的平衡,否则有可能会导致分类器对不同类别的判别能力有着较大的差距,使得分类器进行分类时偏向样本基数大的一方就能得到较高的正确率,进而对实验结果的解释造成影响(Pereira et al.,2009;Carlson et al.,2019)。

3.2.3 模型构建

将数据进行划分后,需要把训练集输入至分类器中,使分类器从数据中按照一定规则找到决策边界,求解出相应的函数来构建分类模型。对于分类器的选择,一般选择线性分类器而不是非线性分类器,主要有以下几点考量：第一,非线性分类器虽然能够拟合更为复杂的决策边界,但这种分类性能的提高往往是以过拟合为代价的,导致其对结果的可解释性比线性分类器差(Kamitani&Tong,2005;Misaki et al.,2010;Carlson et al.,2019;Ivanova et al.,2021)。第二,线性分类器能够将其权重经过处理后投影到EEG/MEG 通道的地形图上(详见下一小节“权重投影”部分),使结果可视化,让人们能够对解码信息的来源有一个更加直观的认识(Haufe et al.,2014)。第三,线性分类器是对来自不同通道的信息进行加权和组合,与大脑神经元的工作原理很像,更符合生物学特性(Kriegeskorte,2011;Ivanova et al.,2021)。因此在认知神经科学的研究中,研究者更加倾向于使用线性分类器进行解码分析,如线性支持向量机(linear support vector machine,LSVM;Cichy et al.,2014,2016;Cichy,Pantazis,&Oliva,2016;Cichy,Kriegeskorte,et al.,2017;Cichy,Khosla,et al.,2017;Charles et al.,2014;Tucciarelli et al.,2015;Bae &Luck,2018,2019a,2019b;Dobs et al.,2019)和线性判别分析(linear discriminant analysis,LDA;Carlson et al.,2011,2013;Kaiser,Azzalini,&Peelen,2016;Kaiser,Oosterhof,&Peelen,2016;Wardle et al.,2016;Fahrenfort,Grubert,et al.,2017;Fahrenfort,van Leeuwen,et al.,2017;Alilović et al.,2019;Linde-Domingo et al.,2019;Barchiesi et al.,2020;Blom et al.,2020)。在具体研究中,单纯地追求更高的解码正确率并非是解码分析在认知神经科学中的主要目标,研究者更重视的是对认知加工过程的神经机制进行合理的阐述(Hebart &Baker,2018;Teichmann et al.,2020),所以在非必要的情况下,线性分类器是最佳的选择。

3.2.4 模型检验

在训练好分类器之后,需要用测试集数据对其进行泛化测试,以评估分类器对于特定认知加工过程的识别能力。泛化测试得到的结果一般是分类器的解码正确率;在前人的研究中,有许多方法被用于在群体水平上对分类器的解码正确率和随机水平之间的差异进行统计检验,如t检验(t-test;Carlson et al.,2011;Allefeld et al.,2016;Bode et al.,2019;Fahrenfort,Grubert,et al.,2017;Fahrenfort,van Leeuwen,et al.,2017;Fahrenfort et al.,2018;Hubbard et al.,2019;Sandhaeger et al.,2019)、贝叶斯因子(Bayes Factors;Wagenmakers,2007;Rouder et al.,2009;Dienes,2016;Grootswagers et al.,2019;Robinson et al.,2019)、Wilcoxon 符号秩检验(Wilcoxon signed-rank test;Charles et al.,2014;Correia et al.,2015;Redcay &Carlson,2015;Sankaran et al.,2018;Linde-Domingo et al.,2019)、置换检验(permutation test;Cichy et al.,2014;Isik et al.,2014;Tucciarelli et al.,2015;Pantazis et al.,2018)等方法。由于以上方法在每个时间点上都对正确率进行了检验,大量的检验会造成多重比较的问题,所以还需要对检验后的结果进行校正。常用的多重比较校正方法有FDR (false discovery rate;Benjamini &Yekutieli,2001;Correia et al.,2015;Redcay &Carlson,2015;Fahrenfort et al.,2018;Heikel et al.,2018;Pantazis et al.,2018)、基于簇的置换检验(cluster-based permutation test;Maris &Oostenveld,2007;Oosterhof et al.,2016;Fahrenfort,Grubert,et al.,2017;Fahrenfort,van Leeuwen,et al.,2017;Kia et al.,2017;Bae &Luck,2019a,2019b;Teichmann et al.,2020)以及Bonferroni校正(Bonferroni;Cichy et al.,2014;Kaiser,Oosterhof,&Peelen,2016;Guggenmos et al.,2018;Sankaran et al.,2018)。以上评估和校正方法都取得了不错的效果,但是它们同样有着各自最适合使用的场景,因此需要结合实际的研究内容来选择具体的方法(Allefeld et al.,2016;Hebart &Baker,2018;Carlson et al.,2019)。

已有的ERPs/ERMFs 研究主要是在关注的通道上(全部通道或者由部分通道组成的通道簇)利用数据空间结构特征逐时间点开展解码分析,但不同研究之间对于数据处理方法的选择并不一致(如预处理采用哪些步骤、怎样对数据进行划分、如何构建模型并对其进行统计检验等),目前还没有一套可供参考的标准化规范,因此研究者在实际分析的时候需要根据自身的数据特点进行综合考量,尽可能选择最合适的方法组合,以保持解码精度和操作步骤数量之间的平衡(Grootswagers et al.,2017;Carlson et al.,2019)。

3.3 基于解码分析的衍生方法

3.3.1 时间泛化方法

时间泛化方法(the temporal generalization method)能够对神经表征随时间变化的稳定性进行描述(Fahrenfort et al.,2018),根据关注的问题类型可具体细分为跨时域解码(cross-temporal decoding)和跨任务/状态解码(cross-task/state decoding)两种方法。其中,跨时域解码通过在特定的时间点上对分类器进行训练,并在所关注时间进程内部的所有时间点上进行泛化测试,利用时间泛化矩阵来揭示不同认知状态下的大脑活动模式是怎样随着时间变化的,使人们对大脑活动模式在时间跨度上的泛化性可以有更为直观的认识(Carlson et al.,2011,2013;Cichy et al.,2014;King &Dehaene,2014;Teichmann et al.,2018;Dobs et al.,2019)。如图6A 所示,矩阵对角线上的结果与常规逐时间点解码分析得到的结果一致,而非对角线上的结果则代表了神经表征随时间变化的情况：如果在某个时间点上训练好的分类器能够很好的对其它时间点上的数据进行预测,说明在这些时间点上大脑对信息的编码模式是类似的;反之,则说明在这些时间点上大脑对信息的编码模式发生了变化,导致该分类器的决策边界不再适用于其它时间点(Carlson et al.,2011;Grootswagers et al.,2017)。

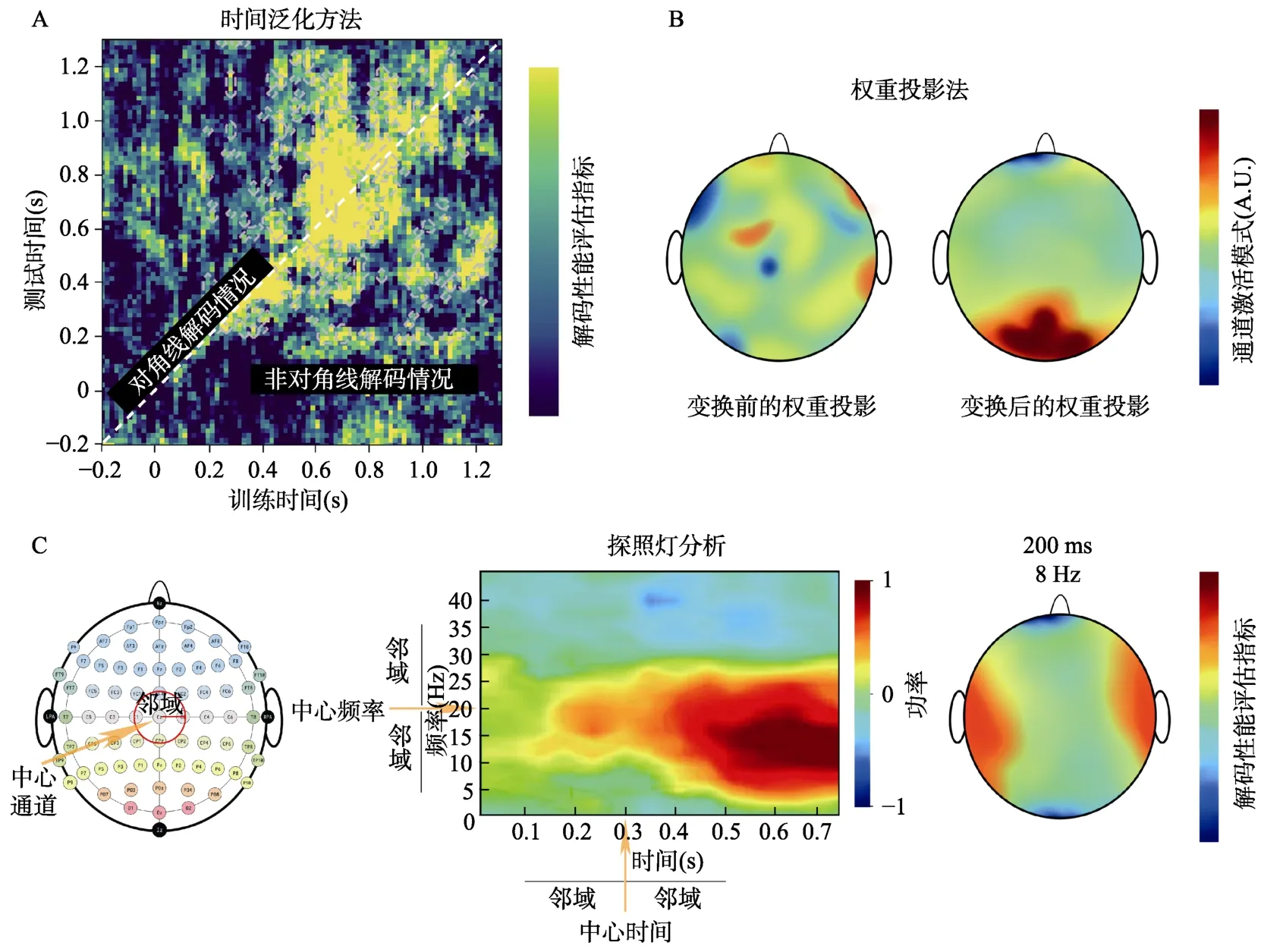
图6 基于解码分析的衍生方法示意图。(A)利用时间泛化方法能够直观地在时间跨度上对刺激呈现后相应的神经表征稳定性进行观察。其中,对角线为常规逐时间点解码分析的结果,非对角线为信息编码模式随时间变化的情况。(B)原始权重投影如左图,由于直接使用各个通道的原始权重值不利于对解码信息的来源做出合理的解释,因此需要使用Haufe 等人(2014)提供的方法对原始特征权重进行变换。如右图所示,变换后的权重投影解释性更强,体现为枕区对于区分不同条件的贡献最大。(C)采用探照灯分析能够在时间、频率、通道维度上对感兴趣的多变量效应进行研究。如左图、中图所示,当以某一时间点、频率或者通道为中心,联合该中心邻域内的其它信息共同构建分类特征,可以帮助人们从时间、功率、空间上探索特定频率下在不同时刻每个通道对分类结果的贡献情况,其结果如右图所示。

跨时域解码用于解释神经表征是如何随着时间动态变化的,跨任务/状态解码则用于揭示不同类型刺激之间的神经表征差异在不同任务状态下的泛化情况(King &Dehaene,2014;Contini et al.,2017)：使用任务A 下的ERPs/ERMFs 数据对分类器进行训练,并对任务B 的ERPs/ERMFs 数据进行泛化测试,可以揭示不同任务状态下大脑对信息编码过程中神经表征的相似性,以及这种相似性是如何随着时间变化的(Isik et al.,2014;Kaiser,Azzalini,&Peelen,2016;Kaiser,Oosterhof,&Peelen,2016;Dijkstra et al.,2018;Blom et al.,2020;Xie et al.,2020)。跨时域解码与跨任务/状态解码的分析流程基本相似,不同之处在于,用于跨时域解码的训练集和测试集是从同一个任务下不同条件的数据中采用交叉验证的方法进行划分所得;用于跨任务/状态解码的训练集和测试集则来自两个不同实验任务下的数据,两个实验任务的数据需要分别作为训练集和测试集来分别完成一次解码,且任务之间的刺激条件要彼此对应(即任务A 的条件M 要与任务B 的条件M 对应,任务A 的条件N 要与任务B 的条件N 对应)。

3.3.2 权重投影

使用考虑特征协方差的线性分类器(如支持向量机、线性判别分析)对多个通道的数据进行解码分析时,除了解码正确率外,还能获取到分类器在各个通道上用于预测的特征权重。根据不同通道的权重信息进行特定的数学变换,可以估计某一通道在分类过程中对于有效信息的贡献情况,进而定位解码信息的主要来源,这便是权重投影(weight projection)方法。

当使用权重投影的方法来说明解码信息的潜在来源时,必须只考虑用于区分不同类别条件之间差异的信号,使得权重只反映每个特征在分类过程中的重要性(Haufe et al.,2014;Fahrenfort,van Leeuwen,et al.,2017;Hebart &Baker,2018;Carlson et al.,2019)。由于来自线性分类器解码之后每个通道的权重不能可靠地被直接解释为神经活动信号的强弱(Haufe et al.,2014),我们可以使用Haufe 等人(2014)描述的一种数学方法,可以提升权重信息的可解释性(图 6B)。以线性分类器LDA 的权重变换为例,该方法将分类器的权重乘以数据协方差矩阵。由于从LDA 中获得的权值包含由协方差矩阵归一化的两个比较集之间的差异,该方法重新生成的通道权重,可以解释为神经源信息。还需注意的是,权重投影法并不适用于滑动窗口这种将多个时间点的数据直接作为输入特征来进行分类的方法(Haufe et al.,2014;Grootswagers et al.,2017;Kia et al.,2017)。

3.3.3 探照灯分析

探照灯分析(searchlight)也称为信息映射(information mapping),主要用于识别局部信息区域特征,以支持在时间、频率、通道上对关注的效应进行定位(Tucciarelli et al.,2015;Oosterhof et al.,2016;Ronconi et al.,2017;Sato et al.,2018)。探照灯分析的中心思想在于,以某一时间点、频率或者通道为中心,联合该中心邻域(neighborhoods)内的其它信息共同构建特征向量来作为用于解码分析的特征集(图6C 左、中),并用计算得到的解码正确率(在探照灯分析中亦被称作度量,measures)作为评估该中心特征对于分类的贡献指标(图6C右)。其中,邻域指的是在探照灯分析中具体使用的时间、频率以及通道半径范围,它定义了实际分析中所使用的区间间隔大小(Oosterhof et al.,2016)。

为了直观体现传统解码分析和探照灯分析的区别,下面以时域解码为例,解码分析的做法是将全部通道(或其子集)的ERPs/ERMFs 数据进行逐时间点分类,探照灯分析则是以每个时间点为中心,将它们分别与其邻域内的时间点进行整合,并对整合后全部通道(或其子集)的数据进行逐时间点分类。如利用64 通道的ERPs 数据进行逐时间点解码,解码分析在每个时间点上用于训练模型的特征数为64×1=64 个,而邻域为2 的探照灯分析还需要包含前后各2 个时间点的信息,因此在某一时间点上需要输入的特征数为64×(2+1+2)=320 个。此时,探照灯分析可以视为尽可能地减少时域上的高频噪音对数据造成的影响,在寻找效应来源的同时增加信噪比,以发掘更加精细的差异。基于ERPs/ERMFs 数据的探照灯分析具有多种形式,同理,当进行逐通道的分析时,则是将每个通道及其邻域内的通道整合为一个通道簇来作为分类器输入特征,以提高空间维度上的信噪比。由于不同的邻域之间可以相互组合,因此还可以使用时间-通道的探照灯分析,在时间、空间上对所关注的效应进行定位,直到获得每个通道在不同时刻对分类结果贡献的映射情况(Tucciarelli et al.,2015;Kaiser,Oosterhof,&Peelen,2016;Kietzmann et al.,2017;Ronconi et al.,2017;Collins et al.,2018;Robinson et al.,2019;Barchiesi et al.,2020;Giari et al.,2020;Teichmann et al.,2020)。以此类推,时间、频率、通道之间也可以进行组合,并且在EEG/MEG 研究中,还可以将时间泛化方法与探照灯分析相结合,实现时间泛化-探照灯分析(Oosterhof et al.,2016)。作为解码分析的衍生方法,利用探照灯分析同样可以描述不同刺激条件下大脑活动模式的细微变化,从而提供新颖的见解(Collins et al.,2018)。

权重投影和逐通道的解码分析/探照灯分析都可以作为对神经活动信号源进行定位的方法,它们对于结果的解释可以是相似的,比如不同神经表征的差异体现在哪些时刻的哪些脑区或者通道上。需要注意的是,这些方法基于不同的算法原理,关注的分别是线性分类器赋予各通道的权重值和解码正确率。因此,即便对于同一批数据而言,这些方法用于计算结果的信息来源并不完全相同。

解码分析能够在一定程度上对不同认知状态下的神经表征差异进行探索和预测,但是其依旧存在着些许不足。具体来说,在神经表征空间中进行解码分析时,主要依赖于分类器去寻找能够将不同大脑活动模式进行分离的最佳决策边界,从而判断不同认知状态下的大脑活动模式是否有明显差异。对于具体是何种表征信息在分类过程中起到了决定性作用、不同的表征信息又是以何种形式在大脑中进行组织的,大脑是怎样表征相同类别刺激中不同客体(例如动物类别中的“黑猩猩”和“狗”的表征)之间的共性与差异,往往难以从解码分析的结果中得知(Haxby et al.,2014;Nili et al.,2014;Popal et al.,2019;Weaverdyck et al.,2020;Freund et al.,2021)。在下一章中,我们将介绍另一种用于弥补上述不足的神经解码方法——表征相似性分析。

4 表征相似性分析

4.1 基本概述

在认知神经科学研究中,经常需要将理论模型与来自不同被试的行为数据、脑影像数据进行比较,由于数据采集方式不同、各种分析方法的测量精度不一等因素,如何跨越不同来源数据之间的差异并将它们进行关联,是许多研究者关注的问题。Kriegeskorte,Mur 和Bandettini 等人(2008)提出了一种叫做 RSA 的模式信息分析(patterninformation analysis)方法用于研究脑活动测量、行为测量和计算建模之间的定量关系。RSA 主要关注的是刺激条件与神经响应水平之间的二阶同构(second-order isomorphism)而非两者之间的一阶同构(first-order isomorphism)：一阶同构直接比较由不同刺激条件所诱发的神经响应水平,例如比较不同被试在分别看到动物刺激与植物刺激时所诱发出的ERPs/ERMFs 的极性、振幅强度、潜伏期等情况(这也体现出传统EEG/MEG 分析对被试的一致性要求更高,当不同个体之间存在较大个体差异时可能难以对结果做出解释);二阶同构则侧重考虑不同刺激类别对应的神经响应水平之间的差异,并且这种刺激属性和神经响应水平之间的关系在抽提后是稳定存在于个体内部的。具体而言,不同被试看到一组动物刺激和植物刺激时所诱发出的ERPs/ERMFs 的极性、振幅强度、潜伏期等情况可能会非常不同,但是每名被试内部均可以表现出在不同刺激类别之间的神经响应水平有较大差异,同时在相同刺激类别内部表现出相似的神经响应水平(Weaverdyck et al.,2020)。RSA 在二阶同构的基础上来表征一组刺激条件之间神经响应水平的相似程度,它更加关注不同刺激条件之间的差异而非具体的表现形式,例如EEG/MEG 的振幅、fMRI 的BOLD 响应信号、行为成绩等数据之间的性质差别非常大(即一阶同构差异很大),但是它们都能对不同的刺激条件进行区分,并且经过抽提后的RDM 可能是类似的(即二阶同构是相似的,如图 4A)。因此,RSA 在具备了足够的统计不变性的情况下为不同个体、不同来源和形式的数据提供了一个标准化的公共表征空间(Kriegeskorte &Wei,2021)。

RSA 通过计算所有可能的两个刺激(包括相同/不同类别之间)组合之间的可区分性或者相似性,来编码不同神经表征之间的相似性结构,并利用RDM 来描述一组刺激条件与其对应的神经响应水平之间的关系。在实际研究中,不同的刺激条件在神经表征空间中会存在着与之对应的响应向量,RDM 记录了所有两两成对的响应向量间距离,这些响应向量对间的距离共同定义了表征几何(representational geometry),它可以在一定程度上反映不同刺激条件的表征性质(Kriegeskorte&Kievit,2013;Kriegeskorte et al.&Diedrichsen,2019;Freund et al.,2021;Kriegeskorte &Wei,2021)。如图4A 所示,RDM 的基本类型是由相同顺序的水平和垂直刺激进行索引的方形对称矩阵,其中对角线表示的是相同刺激条件之间的比较(根据定义,对角线的数值一般为0),非对角线的数值表示的是对应行和列中两个不同刺激条件对之间的差异(该差异可以解释为在表征空间中对应的响应向量间的距离)。原则上根据不同来源数据建立的RDM 都可以用来预测每个刺激对的大脑活动模式相对相似性/差异性(图4、图7),如行为结果(Mur et al.,2013;Redcay &Carlson,2015;Cichy,Kriegeskorte,et al.,2017;Furl et al.,2017;Wang et al.,2018;Dobs et al.,2019)、计算模型(Cichy et al.,2016,Cichy,Khosla,et al.,2017;Wardle et al.,2016;Kietzmann et al.,2017;Pantazis et al.,2018;Kong et al.,2020)、刺激属性(Carlson et al.,2013;Wardle et al.,2016;Furl et al.,2017;Sankaran et al.,2018)、不同类型的神经成像数据(Cichy et al.,2014;Cichy,Pantazis,&Oliva,2016;Cichy &Pantazis,2017)、不同物种(Kriegeskorte et al.,2008;Mur et al.,2013;Cichy et al.,2014;Sandhaeger et al.,2019)等,使得将各个刺激条件之间的差异量化后直接比较不同数据模态之间的差异成为可能(Kriegeskorte,Mur,&Bandettini,2008;Kriegeskorte,2011;Kriegeskorte &Kievit,2013)。由于RDM 本身是一个复杂、高维的结构,为了在低维空间清晰地展现出RDM 包含的表征性质,通常可以采用多维尺度变换(multidimensional scaling,MDS;Torgerson,1958;Kriegeskorte et al.,2008;Carlson et al.,2013;Kietzmann et al.,2017;Pantazis et al.,2018;Sankaran et al.,2018)、t-分布随机邻域嵌入(t-distributed stochastic neighbor embedding,t-SNE;van der Maaten &Hinton,2008;Grootswagers et al.,2019)以及层次聚类(hierarchical clustering;Johnson,1967;Mur et al.,2013;Cichy et al.,2014)来对RDM 进行可视化。

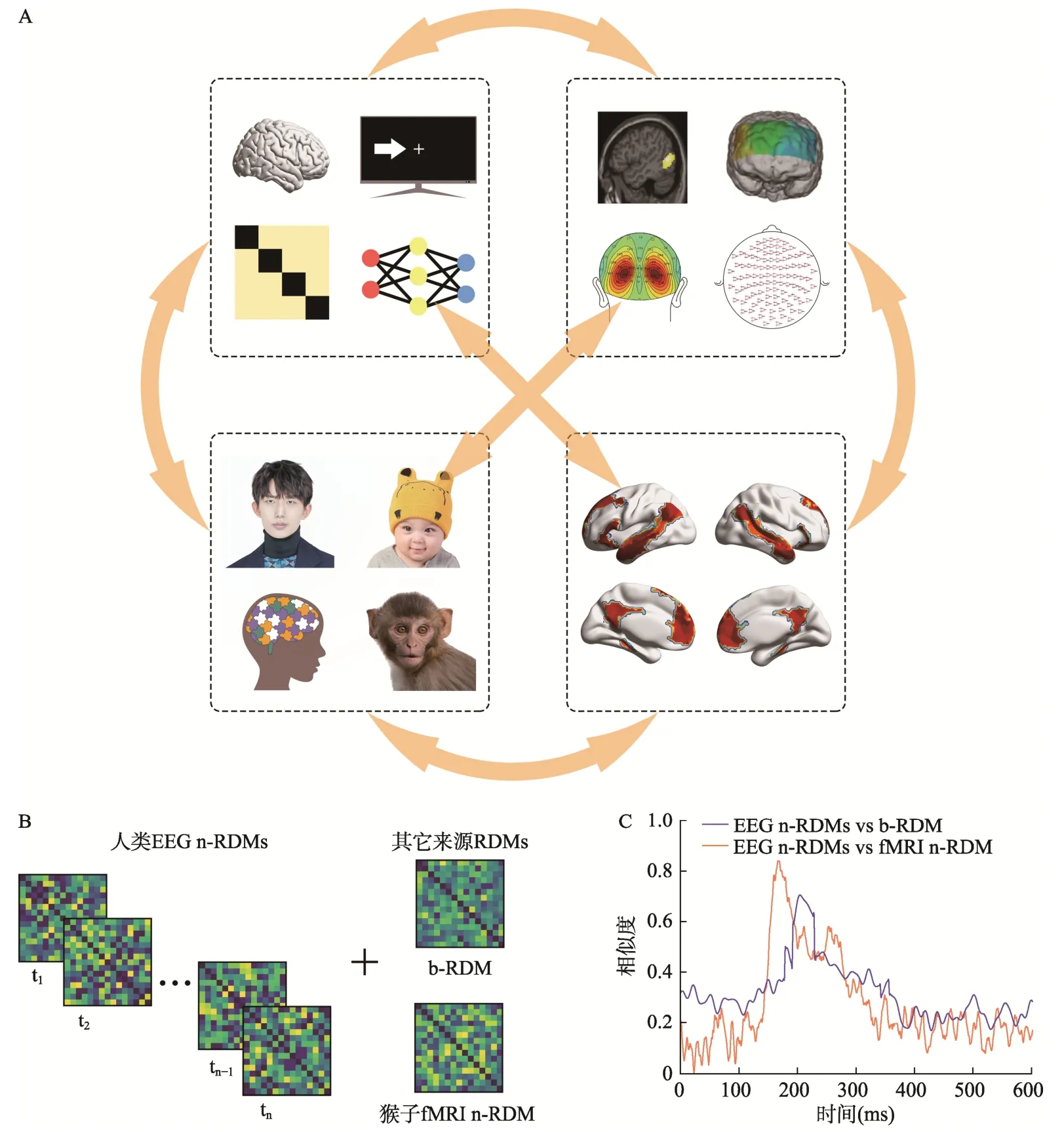
图7 (A)RDM 的来源广泛,它可以在一个公共的表征空间内桥接不同类型的数据,如,跨类别的数据(左上)：根据数据来源的不同,可以从脑活动记录、行为测量、计算建模甚至人工神经网络(artificial neural networks,ANN)中获得的数据来构建对应的神经RDM、行为RDM、模型RDM;跨模态的数据(右上)：根据神经活动记录方式(如fMRI、fNIRS、EEG 和MEG 等)的不同,可以构建不同特点的神经RDM;跨群体的数据(左下)：构建RDM 的数据可以从正常人群(年轻人、婴幼儿、老年人)、疾病人群(孤独症、阿尔兹海默症等)甚至非人类物种(小白鼠、猴子等)这些不同类别的群体中获取;跨脑区的数据(右下)：还可以根据研究者所关注的问题来构建不同脑区所对应的神经RDM。(B)将逐时间点构建的EEG/MEG n-RDMs 与其它来源的RDM 进行比较,可以根据RDM 的来源在时程上从不同的角度对刺激条件之间的神经表征相似性进行探讨。例如,将不同刺激条件下根据人类EEG 活动构建的逐时间点n-RDMs分别与根据行为表现和猴子特定脑区BOLD 响应信号构建的b-RDM、fMRI n-RDM 进行比较,能够得到(C)所示的相似度曲线,可以直观地展现神经活动与行为表现之间的一致性,以及不同物种之间对于相同刺激信息编码的一致性。

4.2 具体算法及实现

4.2.1 构建RDM

在基于RSA 的EEG/MEG 研究中,最重要的一步是构建神经RDM (简称n-RDM)。根据采集到的ERPs/ERMFs 数据,计算不同刺激(同时包含了相同与不相同类别的刺激)的神经响应信号间的相似性,我们可以得到一个n-RDM,它能够表征所有刺激诱发的大脑活动模式差异。考虑到EEG/MEG 包含了多个通道和时间点的数据,以计算单个被试的n-RDM 为例,构建n-RDM 时可以采取以下做法,这两种方法都可以得到各个时间点(或时间窗)的n-RDM,并能够用来观察分析神经表征随时间的动态变化：

(1)逐时间的n-RDM。依次在每个时间点上,将同一刺激条件下的试次进行平均,利用通道信息来计算两个刺激条件间的相似性;或者利用成对刺激条件之间的解码正确率作为该刺激组合的相似性。该做法最后会得到与时间点数量相同的n-RDMs。

(2)逐通道-时间的n-RDM。依次在每个通道上,将同一刺激条件下的试次进行平均,再通过设置时间窗的方式,使得特定时间点的数据包含了对应时间窗内的全部时间点信息(如100 ms 时的数据为以该时间点为中心、前后各20 ms 的全部时间点信息构成的时间窗),再逐时间点计算两个刺激条件间的相似性;或者依次在每个通道、每个时间点上,利用成对刺激条件之间的解码正确率作为该刺激组合的相似性。该做法最后会得到通道数×时间点数个n-RDMs。

行为数据也是常用于构建RDM 的来源之一。类似地,我们也可以根据被试的行为测量结果(正确率、反应时等)直接做两个刺激之间的算术差值(即欧几里得距离)来得到每个刺激对组合间的相似性,并得到用来度量行为任务中不同行为表现间差异的行为RDM (简称b-RDM)。

构建n-RDM 与b-RDM 时相似性度量方法有以下两种：(1)距离法(构建n-RDM 与b-RDM 时均可以采用,例如根据相关距离对多维度的行为学数据构建差异矩阵,对EEG/MEG 数据则可以使用通道或时间点信息作为相关样本来衡量不同条件间的差异;也可以根据欧几里得距离分别对一维的行为学数据、n 维的EEG/MEG 数据间测量值的差异进行衡量;Redcay &Carlson,2015;Furl et al.,2017;Kietzmann et al.,2017;Teichmann et al.,2018;Greene &Hansen,2018;Wang et al.,2018;Giari et al.,2020);(2)解码正确率法(适用于构建n-RDM;Carlson et al.,2013;Cichy et al.,2014,2016;Cichy,Pantazis,&Oliva,2016;Cichy,Khosla,et al.,2017;Redcay &Carlson,2015;Cichy &Pantazis,2017;Guggenmos et al.,2018;Sankaran et al.,2018;Dobs et al.,2019;Grootswagers et al.,2019;Kong et al.,2020;Xie et al.,2020)。无论是计算n-RDM 还是b-RDM,上述过程可以在所有被试上重复进行,并得到一个组平均水平的RDM (Kriegeskorte,Mur,&Bandettini,2008;Nili et al.,2014)。需要注意的是,在选择相似性/差异性度量方式时,要根据原始数据的特点找到一个最合适的度量方式;同时建议在构建RDM 前对矩阵内部的所有数值均被进行归一化处理,以降低数据中的噪声带来的影响(Walther et al.,2016;Guggenmos et al.,2018;Popal et al.,2019)。

除了n-RDM 与b-RDM 外,根据研究的需求有时还要建立包括计算模型和概念模型在内的模型RDM (简称m-RDM),它是研究者根据图像属性、计算建模或者概念属性创建的理论RDM,用于探索不同神经表征对应的时程、脑区、加工模式等信息。m-RDM 可以来自计算模型,包括简单计算模型和复杂计算模型。其中,简单计算模型主要由实验刺激图片的各种物理属性构成,例如图像的低通(low-pass)和高通(high-pass)滤波、色度(colour)、亮度(luminance)、客体的轮廓(silhouette)、Lab 色彩空间中的数字图像以及图像的Lab 联合直方图等,用于量化低水平视觉差异对神经异质性的贡献。而复杂计算模型中RDM 的值是通过一些算法或者函数得到的,主要用于更有理论动机的计算,来模拟某些大脑信息加工过程,如视觉加工的 V1-HMAX 模型、视网膜包络模型(retinal envelope model)等(Kriegeskorte,Mur,&Bandettini,2008;Wardle et al.,2016)。模型也可以是概念性的,概念模型主要强调了不同刺激之间基于某一特定属性的差异,例如动物、植物、人造物品等类别属性,或者有生命、无生命等语义属性(见图4A 根据动植物类别属性构建的概念模型RDM)。概念模型假设在给定的脑区和时程内只能表征特定的信息(例如区分动植物的神经活动),且可以从无关信息中抽取出来,同时不必说明该表征是如何计算得到的,所以可以基于刺激之间的假定关系来创建RDM。例如对面孔进行感知的过程中,大脑可能会对性别、年龄、熟悉性、身份、种族等不同的信息进行表征,此时对于面孔的表征是非特定于某一属性的,但是我们依旧可以使用基于假设创建出的 m-RDM 与实际的n-RDM 或者b-RDM 进行比较,将特定的表征信息给抽提出来(Kriegeskorte,Mur,&Bandettini,2008;Popal et al.,2019)。因此,假设构建的模型能够真实反映出大脑是如何表征不同刺激信息的,那么模型生成的刺激间差异性就可以与实际刺激诱发出的不同大脑活动模式相匹配。

4.2.2 比较RDM

根据研究问题构建完所需的RDM 后,下一步则是在每名被试内部对上述不同来源的n-RDM、b-RDM、m-RDM 进行定量比较,常用的比较方法主要为相关距离,如Spearman 相关、Pearson 相关或 Kendall’s tau 相关(Kriegeskorte,Mur,&Bandettini,2008;Carlson et al.,2013;Cichy et al.,2014,2016;Cichy,Pantazis,&Oliva,2016;Cichy,Kriegeskorte,et al.,2017;Cichy,Khosla,et al.,2017;Nili et al.,2014;Cichy &Pantazis,2017;Kietzmann et al.,2017;Guggenmos et al.,2018;Sankaran et al.,2018;Teichmann et al.,2018;Dobs et al.,2019;Kong et al.,2020;Xie et al.,2020)。一般情况下,除非有非常充分的理由,否则假设不同的RDM 之间存在着线性匹配关系往往是不够合理的,因为RDM 中存在的噪声受到其来源影响,所以在实际研究中更建议研究者使用等级相关距离(例如Spearman 等级相关系数和Kendall等级相关系数)的方式来量化不同RDM 之间的一致性(Kriegeskorte,Mur,&Bandettini,2008;Kriegeskorte et al.,2013;Nili et al.,2014;Popal et al.,2019)。还需注意的是,在比较不同的RDM 时,由于矩阵是按照对角线对称的,为了防止错误地增加RDM 之间的相关性,一般要排除矩阵对角线上的数值,并且只选取对角线上(或下)半部分三角形内的值进行分析(Ritchie et al.,2017;Lu &Ku,2020;Weaverdyck et al.,2020)。

对于高时间分辨率的EEG/MEG 数据,可以根据每个时间点包含的信息或者用于区分两种刺激类型之间差异的解码正确率来构建逐时间点的n-RDMs,并与其它来源的RDMs 进行比较,进而探究不同来源的RDMs 之间的相似性是如何随着时间推移而变化的(图4B、图7B、图7C),帮助人们在时间维度上更好地理解表征信息的编码加工情况(Carlson et al.,2019)。比如,将不同的概念m-RDMs 与逐时间点构建的EEG/MEG n-RDMs进行比较,可以探索大脑对于不同刺激之间某一特定属性差异的表征时程(例如,动植物分类的神经机制从何时开始;Sankaran et al.,2018;Dobs et al.,2019);将b-RDMs 与逐时间点构建的EEG/MEG n-RDMs 进行比较,可以探索特定刺激条件下行为表现与神经活动的一致性(例如,哪个时间段的ERPs/ERMFs 活动可以解释行为上的动植物识别能力;Redcay &Carlson,2015;Cichy,Kriegeskorte,et al.,2017;Dobs et al.,2019);将基于不同感兴趣区(region of interest,简称ROI)的BOLD 响应信号构建的 fMRI-n-RDMs 与逐时间点构建的EEG/MEG n-RDMs 进行比较,可以揭示某一持续神经活动的皮层来源(例如,与动植物识别有关的ERPs/ERMFs 活动来自哪个大脑皮层区域;Cichy et al.,2014,2016;Cichy,Pantazis,&Oliva,2016;Cichy &Pantazis,2017)。

4.2.3 统计推断和模型评估

检验两个RDM 之间的相关性主要采用随机化的方法：将RDM 矩阵的刺激条件标签随机化,根据随机化的结果对两个矩阵中的一个进行重新排序,得到一个新的RDM,并将其与未进行随机排序的RDM 进行比较,计算新的差异性度量。大量重复该过程(例如5000 次),将生成一个置换分布,用于模拟两个RDM 不相关的零假设;把实际相关性与生成的置换分布进行比较,找到其在该分布中的位置,并计算p值,从而比较两个RDM之间是否显著相关(Kriegeskorte,Mur,&Bandettini,2008;Kriegeskorte &Kievit,2013;Nili et al.,2014;Walther et al.,2016;Popal et al.,2019)。

进行群体水平的统计分析则是使用群体水平的相似度和相似度为0 的水平之间的差异进行显著性检验,如果涉及到逐时间点的相似度检验,同样需要对检验结果进行校正(具体的检验方法及校正方法可参照3.2.4 节)。除了在统计水平上检验RSA 的结果是否显著,还需要根据数据的噪声水平计算每个时间点上相应的噪声上限(noise ceiling,具体计算方法请参考Nili et al.,2014),并将其定义为真实模型可能获得的最高相关性,以评估模型的好坏以及实验的局限性(Wardle et al.,2016;Grootswagers et al.,2017;Kietzmann et al.,2017;Pantazis et al.,2018;Sankaran et al.,2018;Teichmann et al.,2018;Greene &Hansen,2018;Dobs et al.,2019;Kong et al.,2020)。

4.3 基于RSA 的衍生方法

时间泛化方法中跨时域解码的思路同样可以推广到基于EEG/MEG 数据的RSA 方法中以进行跨时域比较,具体做法有如下两种：

(1)跨时域RSA。同样根据4.2.1 小节的计算方式直接使用EEG/MEG 数据计算不同条件在任意两个时间点ti和tj上的神经表征相似性,进行逐点比较后得到跨时域RSA 泛化矩阵;或者使用EEG/MEG 数据构建逐时间点的n-RDM 后,将任意两个时间点ti和tj对应的n-RDM 直接比较得到跨时域RSA 泛化矩阵(Lu &Ku,2020;Lu,2020)。该做法类似于跨时域解码,可以对不同条件之间的模式差异进行比较。

(2)动态RSA。假设一共有Ntime个时间点,根据4.2.1 小节的计算方式对任意两个时间点ti和tj的EEG/MEG 数据进行计算并得到跨时域RDMtij;通过对不同的时间点成对计算,最终将得到Ntime×Ntime个跨时域RDMs,再逐个与其它来源的RDMs进行比较,会得到跨时域动态比较后的RSA 泛化矩阵,进而说明不同来源RDMs 之间的相似性在时域上的泛化情况(Cichy et al.,2014;Lu,2020)。

5 应用场景

在认知神经科学的研究中,利用解码分析和RSA 方法,能够使人们对神经表征的模式与特点有更深入的理解。本章节将结合已有的EEG/MEG研究,对解码分析和RSA 的应用场景进行简单的介绍。

5.1 解析不同的认知加工过程

得益于解码分析的高敏感性,研究者能够对感知觉(Wardle et al.,2016;Ronconi et al.,2017;Collins et al.,2018)、注意(Kaiser,Oosterhof,&Peelen,2016;Fahrenfort,Grubert,et al.,2017;Alilović et al.,2019)、语义(Correia et al.,2015;Heikel et al.,2018)、记忆(Bae &Luck,2018,2019a;Linde-Domingo et al.,2019)等内容进行解析,探究不同刺激条件和认知状态下的神经表征差异。例如,在Bae 和Luck (2018)一项关于空间注意和工作记忆的研究中,成功地从ERPs 响应和alpha振荡活动中解码出了低级视皮层对16 个刺激朝向与16 个刺激位置组合的加工,获得了传统分析方法难以得到的精细结果。这也反应了解码分析的部分场景：由于个体差异的存在,如皮层褶皱的差异会导致不同被试对于同一刺激表现的头皮ERPs 活动模式不一样,但是不同刺激诱发产生的ERPs 活动模式在个体内稳定,因此与早期视皮层相关的活动成分可以用解码分析进行区分。解码分析可以帮助我们对不同的大脑活动模式进行提取和学习,并对结果进行预测,从而对不同认知状态下的神经表征进行解析。

此外,由于RSA 的特点之一便是能够对不同时程、不同模态之间的数据进行计算和比较,借助RSA 我们可以对大脑的认知活动有更为深刻的认识。例如,在一项面孔的MEG 研究中,Dobs 等人(2019)将逐时间点构建的n-RDMs 与根据不同概念(性别、年龄、身份、熟悉度)提出来的m-RDMs进行比较,探索了不同时程的n-RDMs 与不同的m-RDMs 之间的相似性,为不同面孔信息的加工顺序提供了新的证据(Dobs et al.,2019)。在一项视知觉研究中,Greene 和Hansen (2018)提取了经过预先训练的深度卷积神经网络(deep convolutional neural network,简称DCNN)中,不同层次的网络对于每张刺激图片的激活情况,并创建了与每层网络相对应的RDM;同时在每个时间点上根据人类被试特定通道的EEG 数据创建了n-RDM。研究者通过比较DCNN 每层网络的RDM 与人类被试的n-RDM,发现在相同的视觉场景分类任务中,DCNN 的各个层次的网络与人类视觉系统处理各个层级之间存在着对应关系,如浅层的DCNN 最能预测0～200 ms 的早期ERPs 活动,而深层的DCNN 最能预测225 ms 左右相对晚期的ERPs 活动,这也为深入理解计算机模型与人类视觉系统之间的关联提供了一个新的角度(Greene &Hansen,2018)。作为一种原理简单、学习成本低的分析方法,RSA 也为我们更深入地理解大脑认知加工过程提供了助力。

5.2 提供神经活动的时间动态特征

EEG/MEG 的优势之一是可以对神经活动进行实时测量,因此结合时间泛化方法能够探究信息加工的动态表征过程。Dijkstra (2018)和 Xie(2020)等研究者利用时间泛化方法对视知觉与视觉想象的共享神经机制进行了探索。研究者使用知觉任务下的信号进行训练来测试想象任务下的信号,以及使用想象任务下的信息训练来测试知觉任务下的信号,发现在特定时间、频率上,知觉和想象之间确实存在着共享神经表征的情况(Dijkstra et al.,2018;Xie et al.,2020)。Blom 等人(2020) 利用时间泛化方法对视觉的预期机制进行了研究,实验人员发现预期机制能够在外界视觉信息实际到达之前,预先激活通常由感官输入信息驱动的神经表征,表明大脑可以对外界信息在接收过程中造成的神经传递延迟进行补偿,使得刺激特异性神经表征和现实事件在时间上尽可能保持同步。该研究通过巧妙的实验设计和时间泛化方法,有力地阐明了特定的神经表征是怎样随着时间的推移而发生改变的。凭借EEG/MEG 高时间分辨率的特点,能够为研究提供神经活动的时序特征,进而为大脑在对信息编码加工过程中的变化情况给出一定的参照依据(Blom et al.,2020)。

基于时间泛化方法跨时域解码的思路,RSA在此基础上也可以采用跨时域比较的方法来探究神经表征加工的动态过程。Cichy 等人(2014)在一项探索人脑对视觉客体加工的时空表征研究中,在相同的刺激条件下采集了MEG 信号和fMRI 信号,首先根据MEG 信号计算了不同刺激对的时间泛化矩阵,利用时间泛化矩阵上每对时间点组合的解码正确率构建了MEG n-RDMs,再分别基于初级视皮层(V1)和下颞叶皮层(interotemporal cortex,简称IT)的体素激活值构建了不同ROI 的fMRI n-RDMs,并将不同时刻的MEG n-RDMs 与不同脑区的fMRI n-RDMs 进行比较,发现在～100 ms和～200-1000 ms 的MEG n-RDMs 与fMRI 的V1 n-RDM 显著相关,在～250 ms 至～500 ms 的MEG n-RDMs 与fMRI 的IT n-RDM 显著相关,这提示视觉系统的不同区域在视觉信息加工的不同阶段提供了瞬时或者持久的神经活动。研究者利用RSA 将高时间分辨率的MEG 信号与高空间分辨率的fMRI 信号结合起来,揭示了不同测量方法下共同的神经表征,对特定神经活动的持续时间和皮层来源进行了识别,在时间和空间上为人类视觉客体加工过程提供了一个完整的分辨视图(Cichy et al.,2014)。将解码分析及其衍生方法和RSA 引入对时间进程更加关注的EEG/MEG 研究之中,前景十分广阔。

5.3 定位神经表征的空间起源

追踪神经表征的时空特征一直是认知神经科学研究中的热点。经典的EEG/MEG 研究中,常用的空间定位方法有利用算法进行源重建(Michel et al.,2004;Sato et al.,2004)或者结合高空间分辨率的fMRI 进行联合记录(Huster et al.,2012;Scrivener,2021),这些方法在实际研究中都取得了不错的成效。随着解码分析的不断普及,一些用于追踪解码信息来源的方法(如逐通道的解码分析/探照灯分析、权重投影)也逐渐兴起,使研究者在EEG/MEG 研究中定位认知活动的空间起源有了更多的选择。利用逐通道的探照灯分析技术,Giari 等人(2020)利用MEG 对文字和图片的神经表征空间特性进行了研究,发现当表达的概念信息相似时,文字和图片的表征涉及到了不同的脑区。在Fahrenfort 和van Leeuwen 等人(2017)一项关于知觉整合的研究中,实验人员对分类器的特征权重进行变换并将重构得到的激活模式映射到地形图上,发现视皮层的知觉整合效应在枕区附近最强烈。许多研究也表明,EEG/MEG 信号中都包含了能够解码认知状态的空间信息,因此解码分析是可以利用不同水平上的空间编码信息来定位神经活动的空间起源(Cichy et al.,2016;Cichy,Pantazis,&Oliva,2016;Cichy,Khosla,et al.,2017;Cichy &Pantazis,2017),并且使用解码分析技术得到的权重值和正确率具有统计学意义,它也为EEG/MEG信号的空间起源定位提供了一些新的视角。

由于RSA 可以将EEG/MEG 数据与其它来源的数据进行联结,因此RSA 也为EEG/MEG 研究提供了追踪神经表征空间特征的方法。Cichy 等人(2014)使用RSA 对视觉客体识别过程中人类大脑皮层的时空动力学进行了研究,研究人员假设对于不同时间、空间分辨率的MEG 和fMRI 数据来说,相同的刺激应具有同样的神经起源,因此会具有相似的神经表征。基于上述假设,研究者构造了基于每个时间点的MEG n-RDMs 和基于不同ROI 的fMRI n-RDMs,并将其分别比较,以寻找客体识别过程中MEG 信号的皮层来源,在毫秒级和毫米级水平上揭示了人脑视觉客体识别过程中的神经动力学(Cichy et al.,2014;Cichy,Pantazis,&Oliva,2016;Cichy &Pantazis,2017)。

6 小结与展望

相比于传统的EEG/MEG 分析方法,解码分析和RSA 能够帮助研究者根据个体独有的大脑活动模式来理解信息编码加工的时程,在保留个体差异的同时对不同个体共有的一致性规律进行抽提,这种特点可以应用于很多涉及复杂场景的实验研究中,为复杂刺激环境中的认知加工机制研究提供了一个新颖有意义的途径。重要的是,解码分析和 RSA 的出现并不是为了替代传统的EEG/MEG 分析方法,而是对已有的方法进行补充,从多角度对不同心智活动下的神经表征差异进行探讨。

尽管解码分析和RSA 两种分析技术在fMRI研究中已经相当的成熟,甚至解码分析都已经在脑机接口(brain computer interface,BCI)领域中得到了广泛的应用,但是直到最近几年才在 EEG/MEG 领域用于研究认知加工活动。值得一提的是,从现有的成果来看,虽然起步时间相对较晚,但在利用EEG/MEG 开展的各类认知神经科学研究中解码分析和RSA 都有着不俗的表现,并且随着研究者们的不断推动以及两种技术在EEG/MEG研究中日益普及,目前也有许多非常成熟的开源工具箱供研究者们使用：在MATLAB 环境下,有CoSMoMVPA (Oosterhof et al.,2016)、the Decision Decoding Toolbox (Bode et al.,2019)、the Amsterdam Decoding &Modeling Toolbox (Fahrenfort et al.,2018)和MVPA-Light (Treder,2020)等;在Python环境下,有 the PyMVPA toolbox (Hanke et al.,2009)、MNE-Python (Gramfort et al.,2013)、NeuroRA (Lu &Ku,2020)和PyCTRSA (Lu,2020)等;其中CoSMoMVPA 和NeuroRA 具有丰富的模块同时支持对EEG/MEG 与fMRI 开展基于分类的解码和RSA 分析。这些工具箱功能强大,能够在不同的开发环境下实现EEG/MEG 的各种解码分析和RSA 方法,使用者可以根据自己的需求和编程习惯灵活选择。

不可否认,作为EEG/MEG 领域的新兴方法,解码分析和RSA 在实际使用的过程中也存在一定的局限性,例如,解码分析和RSA 很大程度上是数据驱动的计算建模方法,缺乏足够的理论假设约束,要获得稳定可靠的结果对数据质量的要求非常高;两种方法的计算量都远大于传统的EEG/MEG 分析方法,要求较高的计算机硬件和更多的运算时间;RSA 需要足够的条件数来获取信服的相关性结果,因此并非所有的实验设计都适合该方法;基于相关方法的RSA 在不同的模型上进行统计检验还有一定的限制,容易受到异常值带来的影响,并且相关分析自身的缺陷对于RSA 的影响也是无法避免的(Popal et al.,2019);解码分析需要大量的试次用于分类器的训练,以学习不同条件之间细微的差别;与传统的EEG/MEG 分析方法类似,随着解码过程中用于统计的通道数增多,也可能会导致更容易得到显著的结果,从而难区分显著的究竟是信号还是噪音;在解码分析的各个阶段,对数据进行哪些处理、选择什么分类器和参数、怎样对得到的结果进行检验和校正,不同的研究者往往会根据自己的经验和实验目的进行具体方法的选择,有时甚至通过反复筛选来得到最优的效果,即便文中已经对不同的方法进行了介绍,但是目前还无法提供一套可供不同研究重复参考的标准,因此解码分析不仅对使用者的先验知识提出了较高的要求,还有一定的可能导致得到的结果在可重复性和可靠性上无法令人信服。

解码分析和RSA 作为目前EEG/MEG 领域分析方法中的后起之秀,为我们理解大脑的认知加工过程提供了一些新的方法与思路。虽然在目前的EEG/MEG 研究中这两种技术还处于起步阶段,但是随着方法学的不断发展,它们仍然有着巨大的潜力与广阔的应用场景。我们认为在今后的研究中,以下方向是值得探究的：

第一个方向是可供不同研究重复参考的分析流程。目前已有的研究中,研究者们更多的是依赖于主观经验来使用解码分析和RSA,而不像传统的EEG/MEG 分析,按照一套标准的操作规范来处理数据。以解码分析为例,数据预处理、归一化、降维、分类器选择、交叉验证、性能评估等都提供了许多种行之有效的操作,对于同一批实验数据而言有非常多的处理方法组合。这可能会导致研究人员受到主观经验偏好的影响,在数据分析过程中选择了不恰当的处理方法,使得最终得到的结果解释性不强。在未来的研究中,针对不同数据的特点以及各类方法最适宜的使用场景,制定一套完善、可供重复参考的数据分析流程,这对于解码分析和RSA 的普及是有好处的。

第二个方向是不同分析方法之间的结合。目前已经有研究者将解码分析得到的解码正确率来代替进行RSA 时使用到的度量指标,以在不同的时间点上构建基于解码正确率的RDM。考虑到在EEG/MEG 研究中,解码分析还存在着许多衍生方法,怎样把这些方法与RSA 有机结合起来,实现跨时域、跨任务/状态对不同时间、条件下的神经表征模式相似程度进行比较,这些都是在未来的研究中值得去进一步思考的。此外,本文涉及的解码分析所使用的模型是一种后向解码模型(backward decoding model,BDM),它与RSA 并不关注EEG/MEG 信号是如何从大脑中生成的,更多地是为了区分不同条件下脑活动之间的神经表征差异(用解码正确率和不相似度来衡量)。近年来在 EEG/MEG 领域还发展了一些诸如群感受野(population receptive field,pRF;Dumoulin &Wandell,2008;Wandell &Winawer,2015)、时间响应函数(temporal response function,TRF;Crosse et al.,2016)、反向编码模型(inverted encoding model,IEM;Sprague et al.,2015)等新方法,它们基于强理论假设,通过不同的建模方法从数据生成的角度来对神经元的响应特性进行模拟,以此来解释不同信号之间的异同(不同的模型对应不同信号的来源,用模型的异同来解释信号来源的异同)。不同类型的方法有着各自的长处与短板,如何将这些方法有机的结合起来以实现更好的分析效果,也是值得探索的方向。