地铁线路坡度对道岔纵向力学特性的影响*

阮 莹 李 平 曾志平 田春雨

(1.广州地铁设计研究院股份有限公司，510010，广州； 2.中南大学土木工程学院，410075，长沙∥第一作者，高级工程师)

GB 50157—2013《地铁设计规范》对正线坡度及道岔的允许铺设坡度要求为：正线的最大坡度宜采用30‰，困难地段可采用35‰；道岔宜设在不大于5‰的坡道上，困难地段可设在不大于10‰的坡道上。然而，在TB 10098—2017《铁路线路设计规范》中，对道岔的铺设坡度规定并没有这么严格：咽喉区外的个别道岔和渡线的铺设坡度不应大于限制坡度。由于地质条件的限制，城市轨道交通中大坡度线路越来越多，部分联络线上的道岔不得不设置在坡度超过10‰甚至坡度更大的坡道上[1-2]。铺设坡度对道岔结构安全性的影响得到了相关专业研究人员的普遍关注。文献[3]研究了坡度对铁路道岔扣件系统性能的影响，提出了减少钢轨磨损和弹条损坏的建议。文献[4]通过建立车-道岔-坡道空间耦合模型，研究了设在坡道上列车-道岔系统的动态响应。文献[5-6]研究了不同工况下坡度对长大坡道桥上无缝道岔受力与变形的影响，研究结果表明：坡度的增大对桥上无缝道岔的受力与变形都是不利的；当坡度增大至20‰时，桥上无缝道岔的纵向力与位移并未超出相关规范要求。

道岔结构形式复杂，在温度变化以及列车制动荷载作用下，道岔钢轨容易产生较大的结构变形和内力。当道岔铺设在大坡度地段时，列车制动荷载增大，结构受力更为不利。为了获得道岔在大坡道上的适应性，本文建立了地铁9号道岔有限元模型，研究不同工况下坡度对道岔结构的纵向位移与受力的影响，分析地铁大坡度线路道岔的结构安全性、纵向力学分布与演变规律。

1 研究内容与计算模型

1.1 研究内容

本文以某地铁线路实际拆解改造工程为例，基于有限元法对地铁9号道岔的纵向力学特性进行研究。首先，对比两种列车荷载模拟方式(均布荷载和集中荷载)，并研究列车荷载的最不利加载位置；在此基础上，分析在列车制动荷载、温度荷载及荷载组合作用下，坡度对道岔纵向位移与受力的影响规律；最后，检算最不利工况下道岔的结构强度和位移，评估列车通过时，大坡度道岔的结构安全性。

1.2 计算模型及其参数

9号单开道岔全长为29.569 m，前长为13.839 m，后长为15.730 m，导曲线半径为200.718 m；基本轨采用60 kg/m钢轨，尖轨为60AT可弯式尖轨，按实际截面采用梁单元模拟；道床和轨枕采用实体单元模拟；全面考虑扣件的三向刚度，扣件横向和垂向刚度采用线性弹簧模拟，扣件纵向阻力使用非线性弹簧模拟[7]；尖轨跟端与导轨、固定辙岔与相连钢轨之间的钢轨接头使用非线性弹簧模拟[8]；辙跟设置间隔铁，使用非线性单元模拟。有限元模型示意图如图1所示。地铁9号道岔结构的计算参数如表1所示。钢轨坐标以列车逆向过岔的方向为正，道岔始端(岔前基本轨端轨缝中心处)坐标为0，道岔终端(辙叉跟端轨缝中心处)坐标为29.569 m。

图1 道岔有限元模型示意图Fig.1 Diagram of turnout finite element model

1.3 列车荷载

该线路采用6节编组的地铁B型车，列车总长为118.6 m，总质量为336 t，车辆定距为12.6 m，固定轴距为2.3 m，轴数为4，轴重为14 t。列车制动力大小受黏着力限制，车轮与钢轨间的黏着力为制动力上限，黏着系数按照UIC(国际铁路联盟)标准取为0.25[7]。

由于车辆振动，作用在钢轨上的动荷载Pd要大于静荷载P0。在模拟列车制动时，引入速度系数α和偏载系数β模拟动荷载对钢轨的作用，Pd可以表示为：

Pd=(1+α+β)P0

(1)

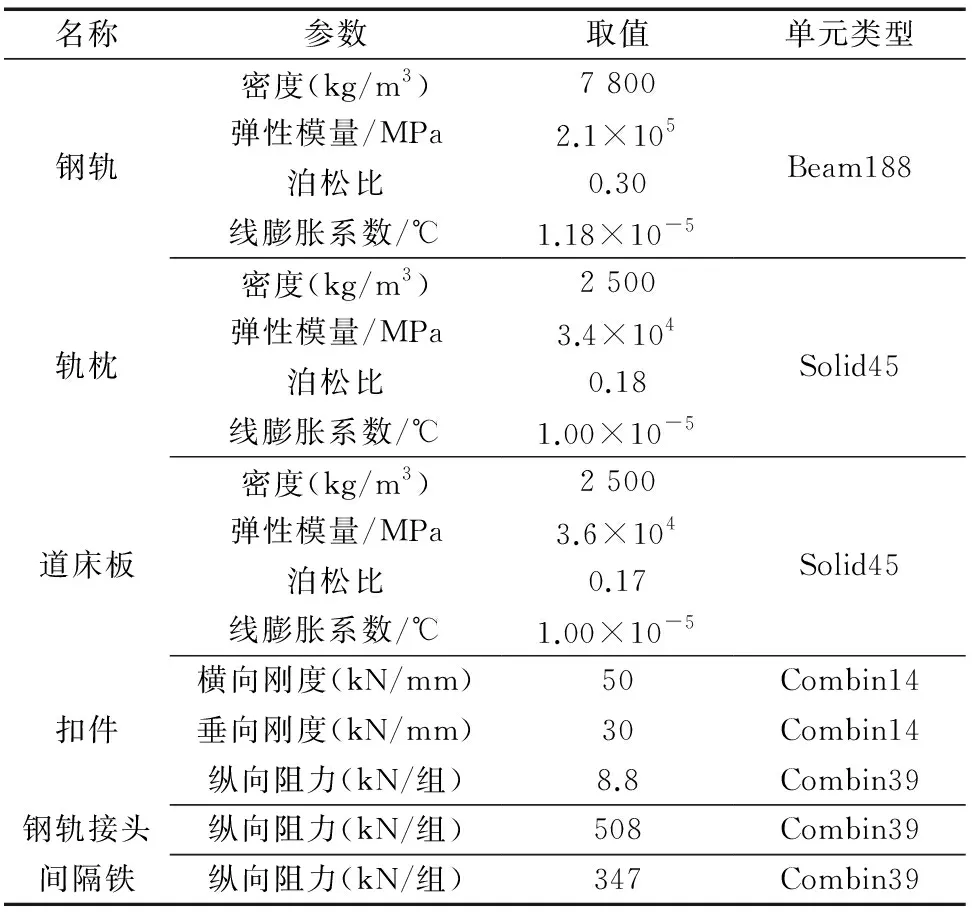
表1 地铁9号道岔结构计算参数Tab.1 Calculation parameters of metro No.9 turnout structure

速度系数和偏载系数可以表示为[9]：

α=0.006v

(2)

β=0.002 Δh

(3)

式中：

v——列车速度，km/h；

Δh——未被平衡的超高，mm。

1.4 检算项目及方法

1) 钢轨强度。道岔钢轨应有足够的强度，在动弯应力、温度应力、列车起动和制动应力及其他附加应力等轴向应力的共同作用下，保证道岔钢轨不失效。根据TB 10015—2012《铁路无缝线路设计规范》，钢轨容许应力[σ]取为363 MPa，其应满足：

σd+σt+σz+σf≤[σ]

(4)

式中：

σd——钢轨最大动弯拉应力；

σt——温度应力；

σf——钢轨承受最大附加应力；

σz——钢轨牵引(制动)应力。

2) 螺栓强度。钢轨接头和间隔铁螺栓以剪切应力不超限为控制标准，普通螺栓直径为30 mm，容许剪应力为264 MPa。根据TB 10015—2012《铁路无缝线路设计规范》，无缝道岔间隔铁应采用的10.9级高强螺栓，其容许剪应力为415 MPa。

3) 可动部分位移。根据TB/T 2614—2005《转辙机通用技术条件》，尖轨与基本轨的纵向相对位移不大于40 mm、叉心的纵向位移不大于20 mm。

2 研究结果与分析

2.1 最不利加载位置研究

既有研究中，列车荷载多由均布荷载模拟，除列车进岔与出岔时外，在列车过岔过程中各钢轨的受力与位移变化较小。然而，地铁9号道岔可弯式尖轨长约为11.2 m，相邻车辆的两个临近转向架相距7.0 m，此处4个轮对相距9.3 m，故最多有4个轮对同时作用在尖轨上。由于轨道所受纵向力因轮轨接触产生，所以仅使用均布荷载模拟列车荷载，无法体现出尖轨上同时作用不同数目轮对时的差别。

分别采用均布荷载和集中荷载模拟列车荷载，对比两种模拟方式对道岔结构受力的影响。以列车侧向过岔为例，将整个过程分为240个加载位置。加载位置示意图如图2所示。

图2 加载位置示意图Fig.2 Schematic diagram of loading position

两种加载方式下，道岔结构的纵向位移、纵向力与加载位置的关系对比如图3所示。两种加载方式下，道岔受力位移变化趋势是一致的。当使用集中荷载加载时，结构受力位移与列车轮对所处位置关系密切，轮对直接作用部位的变化幅度较大。曲尖轨纵向位移与受力存在5个峰值，分别对应B型车5次相邻车辆衔接处的4个轮对同时作用于尖轨时的加载位置。各轨道结构的受力位移图形呈“锯齿”状，而均布荷载则较为“光滑”。

图3 两种加载方式下的道岔结构纵向位移、纵向力与加载位置关系

使用集中荷载时，道岔各钢轨的纵向位移与受力极值均不同程度地大于均布荷载时的数值。在列车荷载的直接作用位置，道岔结构纵向位移和纵向受力增大比例很高，如列车荷载直接作用处曲尖轨的位移与受力增大了50%以上。这说明使用均布荷载的计算结果来检算道岔结构强度及位移是不安全的，其实际结构受力可能更大。因此建议使用集中荷载的计算结果进行道岔强度及位移检算。

采用集中荷载时，道岔结构纵向位移和纵向力极值均大于使用均布荷载，且极值均发生在曲尖轨上。曲尖轨上5个位移和受力峰值依次对应列车的第1节和第2节、第2节和第3节、第3节和第4节、第4节和第5节、第5节和第6节车辆相邻的两个转向架同时作用在曲尖轨上的情况。曲尖轨纵向力最大值出现在第1个峰值，即第1节和第2节车辆相邻的两个转向架同时作用在曲尖轨上时；曲尖轨纵向位移最大值则出现在第3个峰值，即第3节和第4节车辆相邻的两个转向架同时作用在曲尖轨上时。但由于5个受力峰值基本相等，最多相差0.74‰，5个位移峰值则最多相差1.35‰，因此，考虑将曲尖轨纵向位移最不利工况作为最不利加载位置，即当列车的第3节和第4节车辆相邻的两个转向架作用在曲尖轨上时，列车覆盖整个道岔区域，曲尖轨上同时作用4个轮对。

2.2 坡度对道岔纵向变形与受力的影响

在坡道上运行时列车常需制动，此时轨道的纵向力为列车制动力与列车荷载沿坡道方向分力的矢量和，因此坡度会影响道岔结构的纵向力。由于坡道角较小，列车荷载沿坡道的分力方向由坡顶指向坡底,制动力方向与列车运行方向一致。当列车下坡时，制动力方向与列车荷载沿坡道方向分力一致，均由坡顶指向坡底，此时对道岔结构纵向力与变形最为不利。因此本文中的坡度均为下坡。为方便叙述与统计，将曲尖轨、曲导轨、叉心侧股部分组合称为曲侧轨，直尖轨、直导轨、叉心直股部分组合称为直侧轨。

因地铁9号道岔的直股设计速度远高于侧股，出于全面考虑，列车由直股逆向过岔。分别计算铺设坡度为0、5‰、10‰、15‰、20‰、25‰和30‰时，道岔各钢轨的纵向位移、受力与坡度间的关系，计算结果如图4所示。列车通过大坡度道岔时，道岔整体发生与行车方向相同的纵向位移，且位移随着坡度的增大而增大。同时，两尖轨间的相对位移也随着坡度增大而增大。结构受力方面，尖轨跟端所受纵向力较大，且因其通过间隔铁与直基本轨相连，基本轨间隔铁处的钢轨单元受到明显的纵向力。

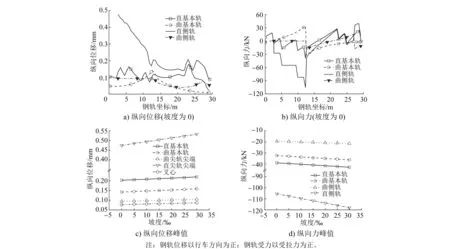
图4 道岔各钢轨的纵向位移、受力与坡度间的关系Fig.4 Relation between longitudinal displacement and force of turnout rails and slope gradient

随着坡度的增加，道岔各部位的纵向位移与受力均呈线性增加。当坡度由0增加至30‰时，基本轨的最大纵向位移由0.203 mm增加至0.224 mm，最大纵向力由38.88 kN增加至42.85 kN；尖轨最大纵向位移由0.475 mm增加至0.532 mm，最大纵向力由105.54 kN增加至118.07 kN。道岔各部位的最大纵向变形与受力均增大超过10%。因此坡度的增大对道岔结构的纵向力与纵向位移均是不利的。

2.3 温度变化对道岔纵向位移与受力的影响

温度变化也会对道岔结构的纵向位移与受力产生影响，道岔温度力示意图如图5所示。由图5可知，道岔终端将承受4根钢轨所传递的固定区温度力或接头阻力，而道岔始端只承受2根的固定区温度力或接头阻力，道岔两端温度力是不平衡的，这将引起道岔钢轨向其始端位移。此外，道岔里轨类似于无缝线路的伸缩区，其温度力将通过间隔铁等传力部件向外轨传递。因此辙跟间隔铁处基本轨的局部温度力增大，采用传统无缝线路的温度力计算公式不够安全，需要采用有限元法计算岔区钢轨温度力。

图5 道岔温度力示意图Fig.5 Schematic diagram of turnout temperature force

根据TB 10015—2012《铁路无缝线路设计规范》中通风系统的相关要求，隧道内温度一般为0～45 ℃，锁定轨温为25 ℃，故轨温最大变化幅度为25 ℃。道岔各钢轨的纵向位移、受力与温度变化之间的关系如图6所示。

图6 道岔各钢轨的纵向位移、受力与温度变化间的关系Fig.6 Relation between turnout rail with longitudinal displacement and force with temperature change

在温度荷载作用下，道岔尖轨尖端的纵向位移最大；辙跟间隔铁处基本轨的纵向位移最大；两尖轨间无相对位移。结构受力方面，由于缺乏纵向约束，尖轨受到的温度力较小；而基本轨类似于固定区，里轨温度力通过间隔铁传递给基本轨，故基本轨承受了较大的温度力。随着温度变化的增大，道岔结构的纵向位移和纵向力都随之呈线性增加。另外，在温度荷载作用下，坡度对于道岔结构的受力与变形几乎没有影响。

2.4 组合工况下道岔的纵向位移与受力

由于坡度与温度变化都会为道岔结构的受力与位移带来不利影响，当两者引起的道岔结构纵向位移与受力方向一致时，荷载组合作用对道岔结构更为不利。因此，研究温度变化为±25 ℃时，不同坡度下列车制动对道岔结构纵向力与纵向位移的影响，如图7所示。

图7 不同坡度下列车制动对道岔结构纵向力与纵向位移影响Fig.7 Influence of train braking on turnout structure longitudinal force and longitudinal displacement under different slope gradients

结构位移方面，当温度变化为-25 ℃时，道岔纵向位移随着坡度的增大呈线性增大，且其位移值大于温度荷载和列车制动荷载单独作用时的位移值。温度荷载不会使两尖轨产生相对位移，因此两尖轨相对位移与列车制动荷载单独作用下一致，随着坡度的增大而增大。当坡度由0增加至30‰时，尖轨的最大纵向位移增加了4.5%，基本轨的最大纵向位移增加了5.7%，叉心的最大纵向位移增加了13.2%。结构受力方面，当温度变化为+25 ℃时，基本轨纵向力较大且随着坡度的增大而增大，辙跟间隔铁处的基本轨单元所受纵向力最大。尖轨所受纵向力的主要来源为列车制动，其也随着坡度的增大而增大。当坡度由0增加至30‰时，尖轨的最大纵向力增加了11.1%，基本轨的最大纵向力增加了1.0%，叉心的最大纵向力增加了0.5%。在荷载组合作用下，随着坡度的增加，道岔各钢轨的最大纵向位移与受力均呈线性增加，对于道岔结构的纵向变形与受力都是不利的。

2.5 组合工况下道岔结构强度与位移检算

当温度变化为-25 ℃、列车制动荷载组合工况下，道岔钢轨位移最大；当温度变化为+25 ℃、列车制动荷载组合工况下，道岔钢轨所受纵向力最大。因此，有必要对列车在最不利工况下通过坡度为30‰的大坡度道岔时的道岔结构强度与位移进行研究，其检算结果如表2所示。由表2可知，在温度荷载与列车荷载组合作用下，即使道岔处于坡度为30‰的坡道上，钢轨强度、螺栓强度和可动部分位移均小于规范中的限值，即强度与位移均满足规范要求，不会发生结构破坏。

表2 最不利工况下道岔结构强度与位移检算结果

3 结语

为研究道岔对坡道的适应性，建立了地铁9号道岔有限元模型，研究在列车制动、温度变化及二者组合作用工况下，坡度对道岔结构纵向力与纵向位移的影响规律。主要结论为：

1) 使用均布荷载与集中荷载模拟列车荷载差别明显，集中荷载更能真实地反映列车过岔时道岔结构的受力与位移情况。当列车第3节和第4节车辆相邻的两个转向架处于尖轨上时，对道岔结构整体受力与位移最为不利。

2) 在列车制动力单独作用下，道岔各钢轨的纵向变形与纵向力随着坡度的增加呈线性增加。当坡度由0增加至30‰时，道岔各钢轨的最大纵向力与纵向位移增大均超过10%。

3) 在温度荷载单独作用下，坡道坡度大小对道岔结构的受力与变形影响可忽略不计。温度荷载与列车制动荷载组合作用时，道岔纵向位移与纵向力随着坡度的增大呈线性增大，且其数值均大于两种荷载单独作用时的数值。

4) 在最不利工况下，即使在坡度为30‰的坡道上，道岔结构钢轨、螺栓强度及纵向位移均满足规范要求。但由于地铁列车行车密度大，在列车牵引荷载和制动荷载反复作用下，坡度对道岔结构安全性与稳定性影响的累积效应还需进一步研究。