高速动车组线性涡流制动系统特性仿真研究
杨利强 徐凯歌 刘赛赛
(1.徐州地铁集团有限公司,221018,徐州; 2.徐州地铁运营有限公司,221018,徐州;3.南京中车浦镇海泰制动设备有限公司,211899,南京∥第一作者,正高级工程师)
线性涡流制动是一种不依靠车轮与钢轨之间的摩擦进行制动的方式,其在高速下可提供稳定、可靠的制动力,已逐渐成为高速列车上一种新型的制动方式[1-2]。但线性涡流制动系统受列车速度、气隙等因素影响,想要获得安全可靠的制动力就要为线性涡流制动系统选取合适的参数范围。
关于线性涡流制动的研究,国内外学者已进行过大量的试验与分析。法国研发的AGV(高速动车组)列车运用的是线性涡流制动系统进行制动,当列车运行速度在200 km/h以上时,每列列车的瞬时制动力可达到20 kN[3-4]。德国从1985年开始在ICE-V(试验型城际列车特快)试验车上进行试验。结合ICE-V试验车的问题及法国AGV列车的经验,德国铁路公司在ICE-3(德国高速动车组ICE的第三代)试验车上对改良后的线性涡流制动系统进行了试验并取得了良好的效果。其研究结果表明:ICE-3试验车使用线性涡流制动系统进行制动时,若动车速度升高,其制动力也能保持较稳定的水平,而制动功率则跟随试验车速度的变化而变化(近似的可以看成线性关系),但线性涡流制动热负荷却比摩擦制动产生的热负荷低很多。这为列车线性涡流制动技术的推广提供了应用基础[5-6]。1964年,日本建成的新干线是世界上第一条高速铁路,长度约为550 km,最快速度可达210 km/h。大约6年后,日本开始在新干线上进行一系列线性涡流制动试验。1990年,日本又开始研究电磁涡流制动技术和永磁涡流制动技术。日本在其高速列车上运用电制动与空气制动组成的联合制动系统进行制动,列车的拖车采用旋转型涡流制动系统作为电制动系统。旋转型涡流制动在高速列车上的成功应用表明,在拖车上使用旋转型涡流制动与空气制动相结合的制动方式是行之有效的[7]。文献[8]以“迎流的”有限元法为基础,推导了涡流制动力公式,并得到其制动力曲线。由该曲线可以看出,随着列车速度的增加,其制动力呈现出先变大后减小的趋势,并在中间某速度处达到最大值。文献[9]对永磁涡流制动器进行了分析,求解出其制动力公式,并分析了不同参数变化对制动力的影响。文献[10]利用德国TR07型磁浮列车的线性涡流制动装置,推导出其制动力的关系式,得到了制动力随列车速度变化的曲线。文献[11]采用子域法计算了线性涡流制动力与速度、励磁电流、气隙长度、板厚和电导率等参数之间的解析公式,并通过有限元仿真验证了理论计算的正确性。由上述研究可知,线性涡流制动系统产生的制动力与所选取的不同参数有关,因此研究不同参数对线性涡流制动系统的影响至关重要。
本文通过ANSYS Maxwell仿真软件对线性涡流制动系统进行建模仿真,分析了线性涡流制动系统在不同车速、气隙、励磁电流及励磁线圈匝数时产生的制动力大小,为线性涡流制动系统的设计提供借鉴与参考。
1 线性涡流制动系统的数学模型
高速列车线性涡流制动系统是由电磁系统和机械系统组成的。电磁系统包括牵引变流器、励磁电磁铁等,其中励磁电磁铁由磁轭、电枢线圈和铁心组成。机械系统一般由升降风缸、套筒等组成。励磁电磁铁与钢轨平行,其包括8个磁极,线圈的电流通入方向使磁极按照“N-S-N-S”交替排列。当高速列车利用线性涡流制动系统进行制动时,钢轨切割电磁铁产生的磁场使钢轨中感应出涡流并形成涡流磁场,该新生磁场将阻碍原本电磁铁产生的磁场变化而使气隙中的磁场畸变产生2个力的分量,其中一个横向电磁力会阻碍列车运动,从而达到列车制动的目的。
由于线性涡流制动力的计算涉及到很多复杂因素,因此,本文根据线性涡流制动系统的工作原理及其在不同工况下的工作过程,采用磁路分析法对涡流磁场进行相应简化,进而建立线性涡流制动力的数学模型。由图1的线性涡流制动磁场示意图可知,磁极与磁极之间构成闭合回路,由于每两个磁极之间形成的回路相同且对称,因此分析电磁铁的电磁机理时,可将多个磁极等效成一对磁极进行分析。

图1 线性涡流制动磁场示意图Fig.1 Diagram of linear eddy current braking magnetic field
根据等效原理,可将磁极与钢轨之间产生的涡流等效成一个半径为r、集肤深度为δ的涡流计算微元。涡流区域磁通是按照余弦规律变化的,因此在钢轨表面产生的感应电动势E为:
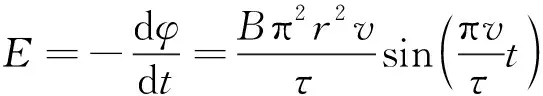
(1)
式中:
φ——线性涡流区域磁通;
B——气隙处的磁感应强度;
v——列车速度;
τ——相邻电磁铁之间的极距;
t——变化时间。
感应涡流在钢轨表面的集肤深度为δ:
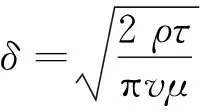
(2)
式中:
ρ——钢轨的电阻率,Ω/m;
μ——钢轨磁导率,H/m。
由式(1)和式(2)可得,涡流有效值λ为:
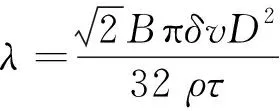
(3)
式中:
D——涡流区域直径,mm。
按照等效磁路原理,对磁路模型各部分磁阻进行等效,得到气隙处的磁感应强度为:
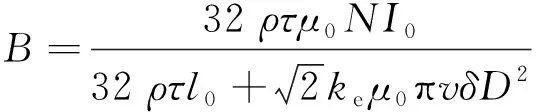
(4)
式中:
μ0——空气磁导率,H/m;
I0——励磁电流,A;
ke——折算系数;
N——线圈安匝数,匝;
l0——气隙长度,mm。
从能量守恒的角度出发,可以得到涡流区域内产生的功率有效值P为:

(5)
根据线性涡流制动力F=Pv,可得:
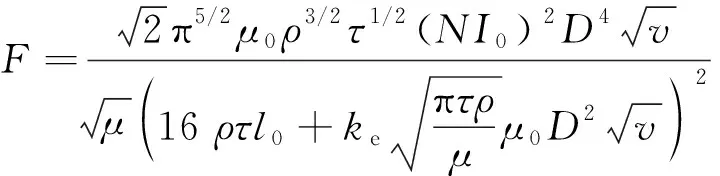
(6)
从式(6)中可以看出,线性涡流制动力与列车速度、气隙长度、励磁电流等诸多因素有关。此外,涡流密度衰减率β可以表示为:
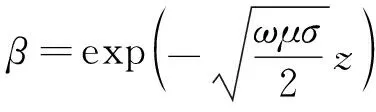
(7)
式中:
z——深度,mm;
ω——涡流频率,Hz;
σ——钢轨电导率,S /m。
由式(7)可知,μ和σ对电流衰减起到了重要作用。当ω不变时,μ或σ越大,则在同一z处衰减得越大[12],因此μ和σ的取值也会影响制动力的大小。
综上可知,列车速度、气隙、励磁电流、励磁线圈匝数、钢轨材料电导率及励磁线圈材料等能够影响线性涡流制动特性和电磁特性。
2 线性涡流制动系统仿真模型
2.1 模型建立
利用ANSYS Maxwell软件建立线性涡流制动系统仿真模型(以下简称“仿真模型”),如图2所示。仿真模型尺寸如表1所示。

图2 线性涡流制动系统仿真模型Fig.2 Simulation model of linear eddy current braking system

表1 线性涡流制动系统仿真模型尺寸
由于钢轨是铁磁性物质,该仿真模型中取其相对磁导率为200 H/m,电导率为5×106S/m;磁轭与磁心的相对磁导率取值为1 360 H/m,电导率为0.153 8 S/m;励磁线圈选铜材料。
为保证仿真模型计算的准确率,要对模型进行剖分;由于线形涡流制动系统会在钢轨表面产生涡流,所以针对钢轨要按照集肤深度进行剖分。线性涡流制动系统网格剖分图如图3所示。

图3 线性涡流制动系统网格剖分Fig.3 Grid division of linear eddy current braking system
2.2 制动特性仿真
常用制动时,线性涡流制动系统励磁电流I0≤78 A;紧急制动时I0为95 A。气隙长度l0变化范围为6~8 mm,制动特性试验参数如表2所示。

表2 制动特性试验参数
2.2.1 励磁电流对制动力的影响
设定不同励磁电流I0研究其制动力与速度变化之间的关系,如图4所示。由图4可知,不同励磁电流下的曲线变化趋势基本一致。当气隙长度保持不变时,增加励磁电流值,制动力数值也随之增大,说明励磁电流与制动力成正相关,这也符合制动力数学模型。在励磁电流分别为60 A、78 A、95 A时,其相应的最大制动力分别约为10.538 0 kN、15.100 9 kN、19.887 8 kN。由此可见,当励磁电流约增加30%时,其制动力增加了44%。
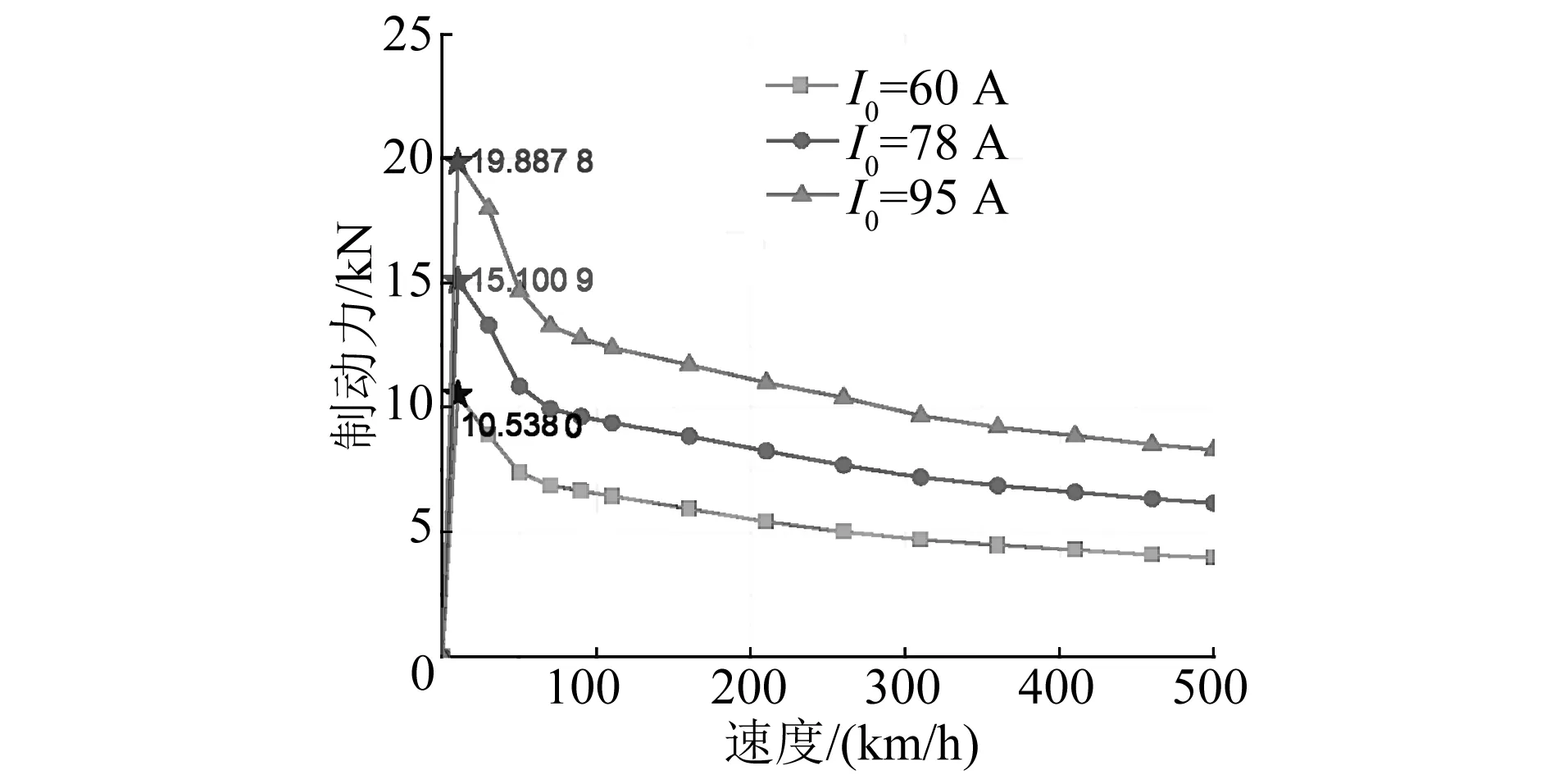
图4 不同励磁电流下制动力随速度变化曲线
2.2.2 气隙长度对制动力的影响
保持励磁电流不变,通过改变气隙长度l0来观察制动力的变化,如图5所示。
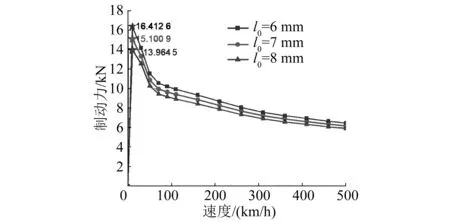
图5 不同气隙长度下制动力随速度变化曲线
由图5可知,随着气隙长度的增加,其制动力曲线峰值不断下降。气隙长度越小,制动力曲线的变化趋势越大,且制动力呈明显增大的趋势。这是因为磁场强度与磁路中磁阻大小有关,气隙长度增大造成了磁阻增大、磁场强度减小,使得涡流密度降低,因此制动力有所下降。当气隙长度分别为6 mm、7 mm、8 mm时,其相应的最大制动力分别为16.412 6 kN、15.100 9 kN、13.964 5 kN。由此可见,当气隙长度减小约33%时,其制动力减小了17.2%。
此外,综合图4和图5可知,涡流制动力受速度影响较为明显,速度越大,制动力曲线上升速度越快,当速度为10 km/h左右时就可以达到涡流制动力的最大值,此时动车速度称为临界速度。当速度持续增大到高速区时,涡流制动力呈下降趋势,最后趋于某个稳定值,总体来说在高速状态时呈良好的制动状态。
2.2.3 励磁线圈匝数对制动力的影响
为研究励磁线圈匝数变化对制动力的影响,选取列车速度在50 km/h、250 km/h、500 km/h时进行分析,研究不同匝数对制动力变化的影响。在相同的条件下,取励磁线圈为280匝、380匝、480匝、580匝分别进行计算,得到3个速度下不同励磁线圈匝数的制动力变化曲线,如图6所示。
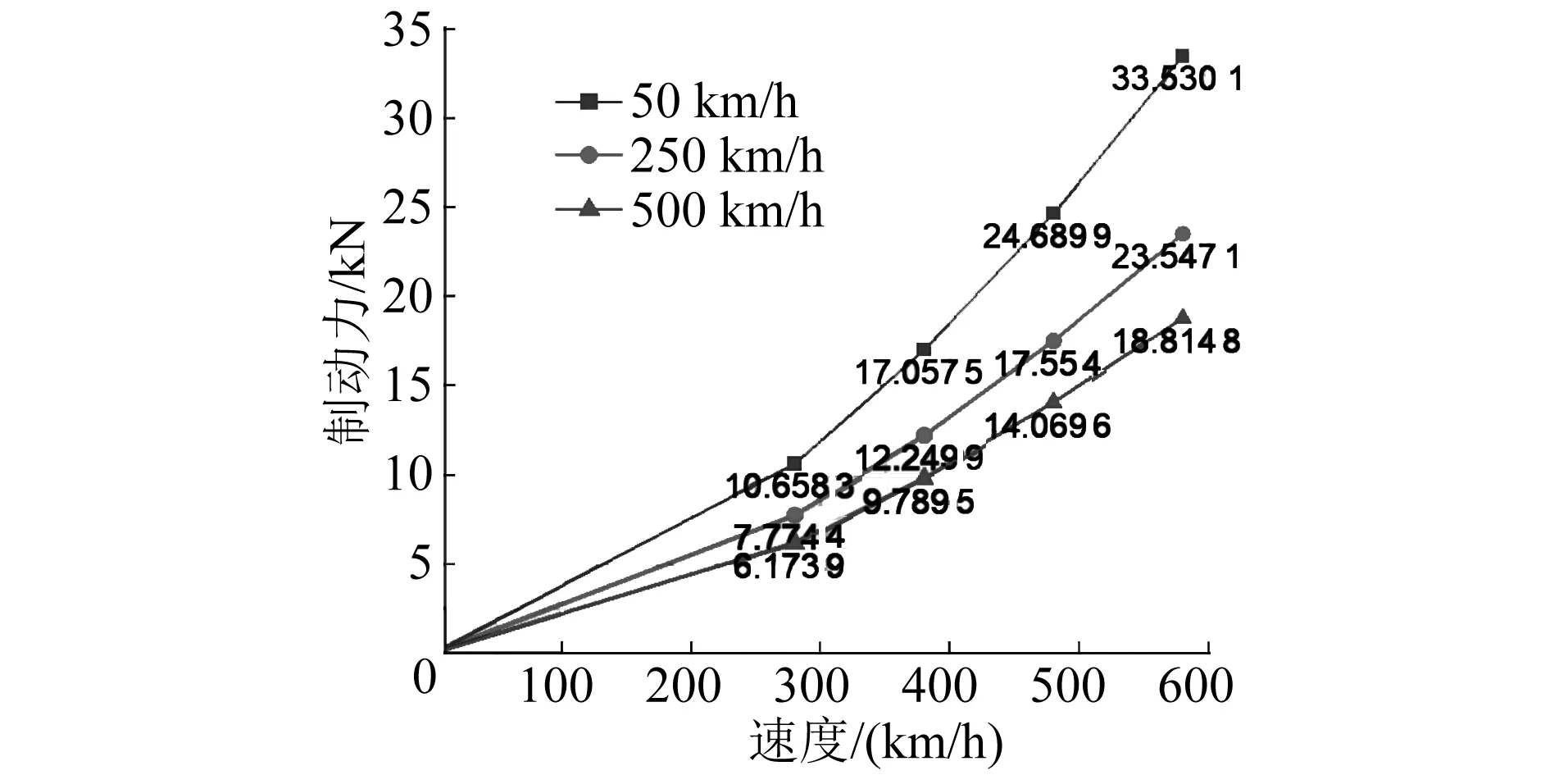
图6 不同列车速度下励磁线圈匝数对制动力变化的影响曲线
由图6可知,当速度为50 km/h时,制动力增加速度最快;当速度为500 km/h时,制动力增加速度最缓慢。由此可见,当励磁线圈匝数增加时,低速运行的列车制动力增加更快,符合制动力的变化规律。
在列车运行速度为50 km/h下,励磁线圈匝数为580匝时的制动力为33.500 0 kN;励磁线圈匝数为280匝时的制动力为10.700 0 kN。由此可见,励磁线圈匝数增大107%,其制动力增加了214%,可见制动力增加的倍数远大于匝数增加的倍数,即增加线圈匝数可以有效提高制动力。
2.2.4 钢轨电导率对制动力的影响
保持励磁电流为78 A、气隙长度为7 mm、励磁线圈匝数为280匝不变,将钢轨电导率σ分别变为原来的2倍、4倍,并对模型进行计算,得到不同磁导率下制动力随速度变化的曲线,如图7所示。
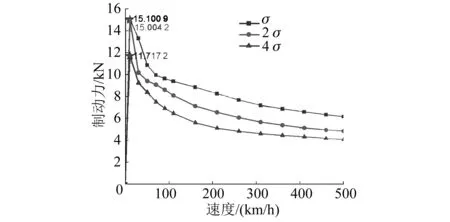
图7 不同钢轨电导率下制动力随速度变化曲线
由图7可知,当钢轨的电导率越大,涡流制动力反而越小。由此可知,钢轨的材料特性对涡流制动力有较大的影响。选择钢轨材料时,在符合工程条件的前提下,应尽可能选择电导率较小的材料,才能有更好的制动性能。
2.2.5 励磁线圈材料对制动力的影响
在保持励磁电流为78 A、气隙长度为7 mm、励磁线圈匝数为280匝时,将励磁线圈材料由铜换成铝,将相同结构的铜线圈与铝线圈的涡流制动系统产生的制动力进行对比,得到不同速度下的制动力曲线,如图8所示。

图8 采用铜线圈和铝线圈时的制动力随速度的变化曲线
从图8中可以看出,在匝数相同的情况下,不同速度下铜线圈产生的涡流制动力与铝线圈的涡流制动力变化趋势一致,但铝线圈的涡流制动力比铜线圈的涡流制动力略大,说明在线圈匝数、气隙长度、线圈励磁电流相同的条件下,选用铝线圈获得的涡流制动力效果更好。
2.3 电磁特性仿真
本节主要分析列车速度为400 km/h时,常用制动和紧急制动下的磁感应强度分布情况。通过上述分析,线性涡流制动系统参数选择励磁电流I0为78 A、气隙长度l0为7 mm、励磁线圈材料为铝线圈。其分析结果如图9—图12所示。

图9 励磁电流为78 A时涡流制动系统磁场分布云图(常用制动工况)

图10 励磁电流为78 A时气隙磁场分布(常用制动工况)

图11 励磁电流为95 A时涡流制动系统磁场分布云图(紧急制动工况)
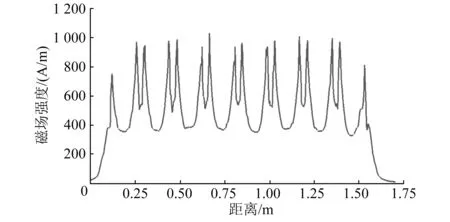
图12 励磁电流为95 A时气隙磁场分布(紧急制动工况)
由图9可知,在磁极附近磁场强度最强,随着与磁极距离越远,磁场强度呈衰减趋势。由于相邻磁极之间形成闭合回路,在单个磁极上方磁轭处两侧的磁感应强度大于中间的磁感应强度。此外,在相邻磁场的叠加作用下,钢轨表面产生了较强的磁感应强度。由图11可知,紧急制动工况下,磁感应强度的分布情况与常用制动工况下基本一致。同时,由于紧急制动工况下励磁电流增大,使得涡流制动系统的整体磁感应强度有所增强。
由图10和图12可知,两种制动工况下的磁感应强度的变化趋势基本一致,但紧急制动工况的磁感应强度值要大于常用制动工况。气隙长度处的磁场强度在相邻磁极之间磁场较强,在涡流制动装置两侧存在磁场泄露的问题,在短距离下会迅速衰减为0。在常用制动情况下,气隙长度处的磁场强度最高可达到877.640 kA/m,紧急制动下可以达到1 030.595 kA/m。
通过上述分析说明,紧急制动工况下,涡流制动系统可以产生更强的磁感应强度和更高的制动力,以保证列车的运行安全。
3 结论
1) 本仿真研究得到的制动力曲线变化趋势符合涡流制动力数学模型中各参数对制动力的影响规律,从而验证了仿真模型的正确性。
2) 涡流制动力随着速度的增加先增大后减小,在某个中间速度值达到临界点。气隙长度增加,涡流制动力增大;励磁电流增加,涡流制动力增大。
3) 当励磁线圈匝数增大后,涡流制动力增加的倍数大于励磁线圈匝数增加的倍数,说明增加线圈匝数可以有效提高涡流制动力。
4) 当励磁线圈材料为铝时,与铜线圈相比,其制动力有所增加。在符合工程的条件下,可以考虑将励磁线圈材料选为铝线圈。
5) 当增加钢轨材料电导率时,发现涡流制动力反而下降,说明钢轨材料电导率与涡流制动力成负相关。因此在符合工程的条件下,选择电导率较小的钢轨材料可以获得更好的涡流制动效果。
6) 紧急制动工况下,涡流制动系统可以提供更强的磁场、产生更大的涡流制动力,以保障列车的运行安全。

