毫米级球状沙尘颗粒连续冲击损伤的力学模型与数值模拟研究

游文俊，王计真，杨强，詹志新，胡伟平

1.北京航空航天大学，北京 100191

2.中国飞机强度研究所 结构冲击动力学航空科技重点实验室，陕西 西安 710065

钛合金是航空、航天等领域重要的结构材料，航空发动机叶片等多采用钛合金材料。在沙漠环境中，航空发动机叶片容易受到空气中沙尘微粒的连续冲击作用，产生凹陷、撕裂、微裂纹等损伤，从而影响其高周疲劳性能。因此，有必要开展沙尘颗粒连续冲击损伤的力学模型与数值模拟研究。

目前，国内外学者大多采用基于试验的分析方法和数值模拟方法研究外物对结构的冲击作用，并取得了一定的成果。外物冲击的试验分析方法主要有机械加工缺口法、低速冲击法、准静态挤压法和高速弹道冲击法。低速冲击法包括摆锤法和螺线枪法，高速冲击法包括枪弹法和空气炮法。J. Dunham等[1]利用机械加工缺口的方法分析了三种金属材料对缺口的敏感程度。Hu Dianyin 等[2]对钛合金叶片边缘采用落锤冲击的方法模拟外物冲击，并通过电镜扫描分析冲击损伤部位，发现冲击切口具有大塑性变形、材料堆积、材料褶皱、阶梯解理、液滴结构和微裂纹等典型特征。Mall 等[3]用静态挤压法在钛合金平板上模拟外物冲击，研究结果表明，准静态挤压方法能模拟出明显的塑性变形，损伤深度越大，越容易出现剪切裂纹。B. Lin等[4]利用高速弹道冲击法模拟了立方体冲击物冲击激光喷丸强化后的翼型叶片前缘，并分析了冲击残余应力的分布规律。M.W.Crowell 等[5]利用气枪进行外物冲击叶片涂层试验，研究外物冲击对涂层的破坏作用。Nesredin 等[6]利用改进的气枪进行外物冲击有涂层窄叶片前沿的试验，分析了冲击对叶片造成的损伤。吴松波等[7]在新型冲击磨损试验机上开展了硬质沙粒冲击TC4钛合金的试验，研究了沙粒粒径、冲击次数对TC4钛合金冲击磨损行为的影响，研究结果表明，粒径和冲击次数能显著影响TC4 钛合金的冲击磨损行为。Yan Cheng 等[8]利用带拉瓦尔喷嘴的空气炮装置研究了沙粒高速冲击Ti-6Al-4V叶片，揭示了叶片破坏与沙粒冲击速度和冲击角度的关系。Wheeler 等[9]利用高速冲击装置研究了沙粒冲击金刚石涂层的损伤机制，通过电镜扫描损伤部位，发现周向裂纹和微空洞是主要破坏特征。张宇等[10]基于二级空气炮系统对V形铝合金靶板进行了高速冲击试验，发现其破坏模式为局部剪切冲塞，射弹角和射弹间距对塑性区大小有显著影响。王计真[11]采用一种初始应力复合材料高速冲击试验方法，对复合材料层合板开展了高速冲击试验，研究发现面内初始应力对复合材料板高速冲击行为影响显著。

数值模拟方法的相关研究主要是基于有限元方法的仿真计算。韩璟圳[12]在ABAQUS平台利用J-C本构模型和损伤演化模型，进行外物冲击轻型点阵结构数值模拟，并通过分析损伤面积，得出不同角度对点阵结构冲击损伤的影响。凡金金[13]进行了沙粒碰撞平板数值模拟，并研究了沙粒碰撞后的反弹特性。唐飞燕等[14]采用计算流体力学（CFD）技术模拟风沙场得到沙粒速度，基于动量定理和冲量等效原则研究了沙粒对建筑物的冲击作用。Chen[15]借助ABAQUS 软件的显示动力分析模块对钛合金的外物冲击损伤过程进行了模拟，采用率相关本构模型计算了冲击变形过程。P. Duo等[16]利用LSDYNA软件动力分析模块开展外物冲击数值模拟，研究了外物损伤的残余应力分布，并且与试验结果进行了对比，发现该数值模拟方法与试验结果吻合较好。D. Williams 等[17]采用 DYNA3D 软件分析了FOD 的动态冲击过程，结果表明，低速冲击条件下的数值模拟结果与试验结果吻合很好，冲击过程中只发生了材料屈服，没有失效。P. H. Tranter 等[18]基于修正的 Zerilli-Armstrong模型对FOD进行了模拟，研究表明Goldthorpe路径相关失效模型能够很好地模拟多种冲击损伤。

本文开展了毫米级球状沙尘颗粒连续冲击损伤的力学模型与数值模拟研究。首先，推导了损伤耦合的J-C本构模型和连续冲击损伤模型。其次，编写Vufield 子程序和Python 脚本，实现了连续冲击损伤计算的数值计算。通过将计算结果与文献中的试验数据进行对比，验证了该方法的有效性。最后，分别进行单个和多个沙粒连续冲击叶片的数值模拟，分析了冲击变形、残余应力和冲击损伤的变化规律。

1 理论模型

1.1 损伤耦合的J-C本构模型

高应变率情况下，材料的应力应变关系通常采用率相关本构方程来描述，其中Johnson-Cook 方程就是一种很好的描述大多数金属动态塑性行为的本构模型，其方程形式如式（1）所示

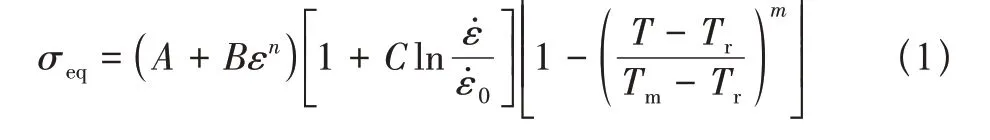
式中，σeq为等效应力；ε为等效塑性应变；ε̇为应变率；T为工件当前温度；ε̇0为基准应变率；Tr和Tm分别为室温和材料熔化温度；A、B、C、m、n是材料常数。

冲击会造成损伤，造成材料劣化，冲击引起的材料劣化可以用连续损伤力学中的损伤变量来表示。对于各向同性损伤，损伤变量D可以表示为代表性体积单元（RVE）刚度的劣化率。

式中:E为无损伤的弹性模量；ED为含损伤RVE 的弹性模量。

则耦合损伤的J-C本构模型表示如下

1.2 连续冲击损伤模型

基于上述损伤耦合的J-C本构模型所计算得到的冲击应力应变，可根据式（5）计算由塑性变形引起的损伤

若沙尘颗粒连续冲击i次，设第i次冲击结束后，损伤为Di，在进行第i次冲击时，将第i-1 次冲击结束后的场变量（包括应力应变）作为第i次冲击的初始场，并将第i-1次的损伤Di-1作为第i次冲击的初始损伤代入式（4）中，可计算第i次冲击的等效应力和等效塑性应变，同时将等效应力和等效塑性应变以及Di-1代入式（7）可计算损伤增量ΔDi，然后由式（8）得到第i次沙尘颗粒冲击后的损伤Di。进而得到第i次冲击后的残余应力、残余应变及冲击损伤

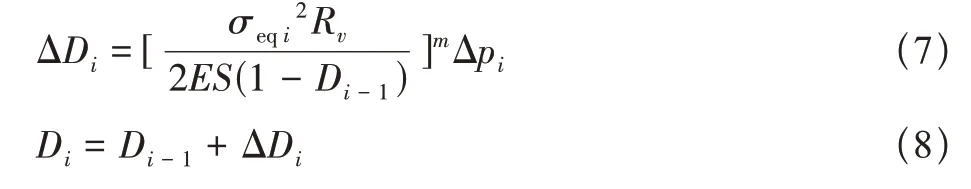
2 材料参数标定

有两类材料参数需要标定，即J-C本构模型参数和连续冲击损伤模型参数。本文叶片的材料为Ti-6Al-4V钛合金，其基本力学性能参数见表1[2]，该材料的J-C 本构模型的参数取自参考文献[2]，见表2。根据Ti-6Al-4V钛合金试验件的低周疲劳试验，采用最小二乘法可确定冲击损伤模型中的参数S和m，见表3。

表1 Ti-6Al-4V静力性能参数［2］Table 1 Static mechanical properties of Ti-6Al-4V［2］

表2 J-C本构模型参数的材料参数［2］Table 2 Material parameters of the J-C constitutive model［2］

表3 Ti-6Al-4V冲击损伤计算模型参数［19］Table 3 Parameters of Ti-6Al-4V impact damage calculation model［19］

3 连续冲击损伤的数值模拟

3.1 数值计算方法

基于ABAQUS 平台，实现损伤耦合的J-C 本构模型和冲击损伤模型的有限元数值计算。计算流程简述如下:（1）初始化所有参数。（2）在ABAQUS 平台建立有限元模型，包括划分网格、材料属性设置、叶片边界条件设置、接触属性设置（包括接触算法设置和摩擦系数设置）、设置分析步为显式动力学。此外，在设置分析步时，分析步时间的设置应满足冲击物与叶片接触后完全分离。（3）将损伤耦合的J-C本构模型和冲击损伤模型编写为Vufield 子程序并嵌入ABAQUS Explicit Dynamic 模块计算应力应变以及冲击损伤。（4）前一次冲击结束后，利用Python 程序将该次产生的损伤、残余应力应变和变形导入下一次冲击计算模型作为初始场。利用Python程序设置工况，包括沙粒尺寸、沙粒个数、冲击速度、冲击角度、连续冲击次数， 以实现不同工况的连续冲击。

3）1985－2000年，巢湖流域的8个评价单元全部为负值，表明土地利用程度衰退是该时间段内巢湖流域的主要趋势，人类活动对土地利用程度的影响较小。

3.2 数值模拟方法的有效性验证

本文采用一次冲击的试验数据对上述数值模拟方法进行验证。虽然沙粒和钢球的特性差异很大，但是二者的硬度均远大于钛合金，本文采用了钢球撞击试验来验证所提的分析方法。 J. O. Peters等[20]利用直径为3.2mm的钢球在高速（200m/s、250m/s、300m/s）下垂直冲击Ti-6Al-4V 试件，得到的冲击凹坑的结果见表4。该试验中，钢球的密度为7850kg/m³，试件的冲击示意图如图1所示。

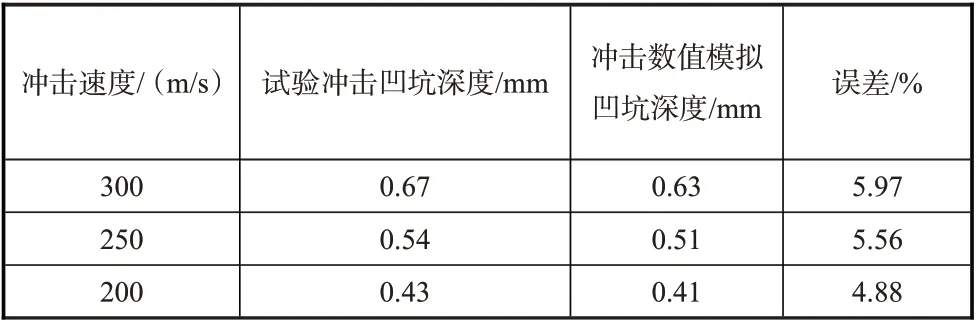
表4 冲击凹坑深度的数值模拟结果Table 4 Numerical simulation results of pit depth

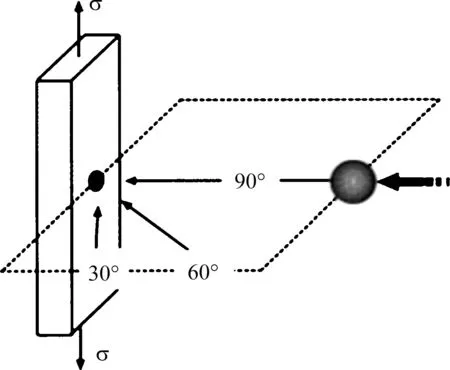
图1 冲击示意图[19]Fig. 1 Ⅰmpact diagram[19]

首先，建立有限元模型，采用网格局部细化法对模型划分网格，如图2 所示，模型共有120600 个单元、127402 个节点，单元最小尺寸为0.1mm。边界条件为两端固定。材料属性方面，钢珠设置为刚体，钛合金叶片的材料参数见表1 和表2。其次，设置接触属性，采用通用接触，摩擦系数设置为0.15。然后，设置分析步时间为1e-5s，以保证钢珠和叶片接触后可完全分离。最后，编写Vufield 子程序并嵌入ABAQUS Explicit Dynamic模块，实现冲击模拟，得到冲击响应。本文施加的冲击物的冲击速度分别为200m/s、250m/s和300m/s，冲击凹坑的云图如图3所示，提取凹坑最大深度的结果见表4，可以发现，数值模拟与试验结果相近，误差在允许范围内，验证了所提数值模拟方法的适用性。此外，对于300m/s 的冲击速度，计算得到如图4 所示的初始冲击损伤分布云图，将其与参考文献[20]中的实验观测的电镜图（见图5）进行对比，发现电镜图中的微裂纹分布规律与初始损伤云图的分布规律有一定的相似性。

图2 有限元模型图Fig.2 Finite element model

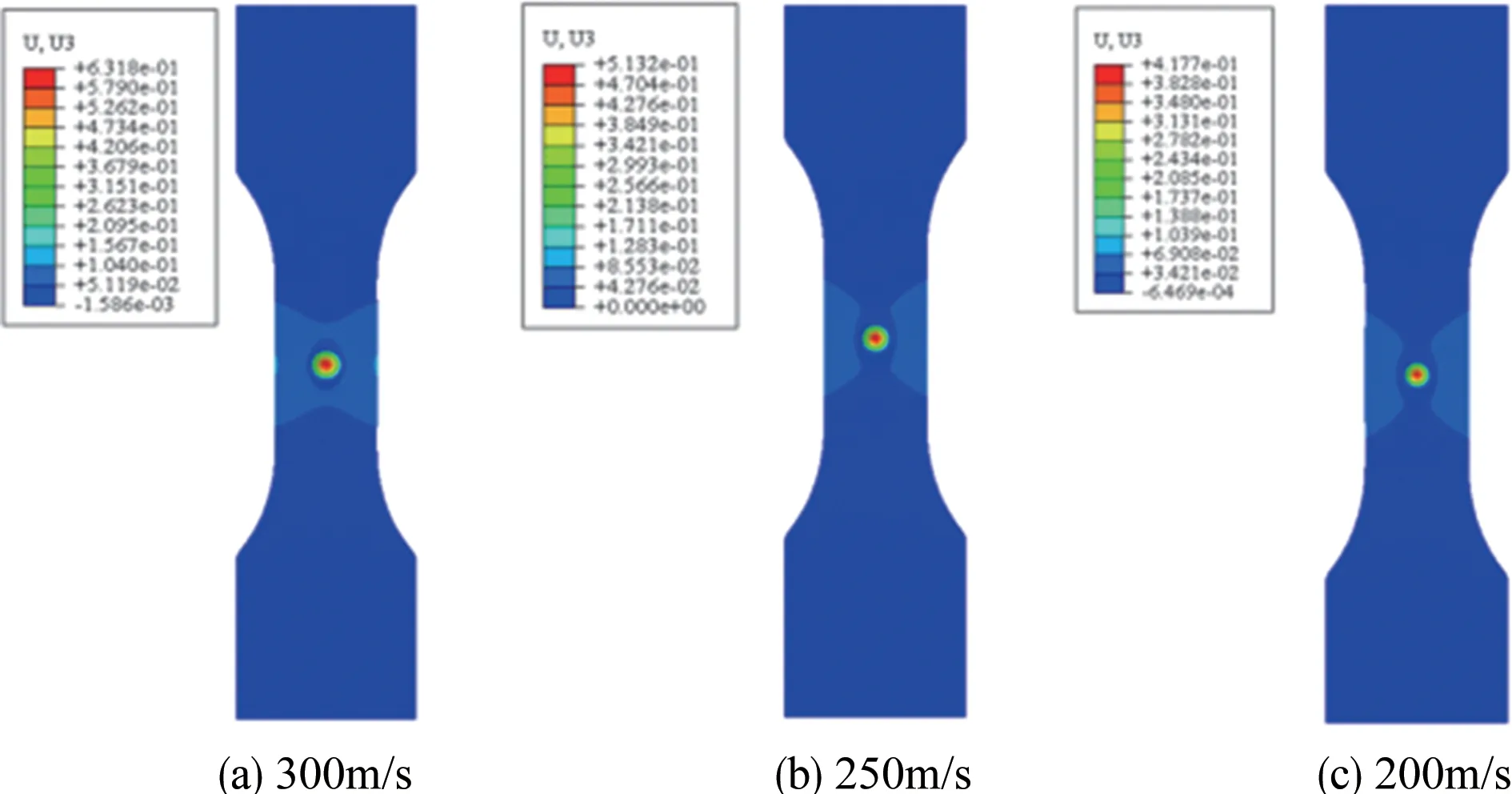
图3 冲击变形图Fig.3 Ⅰmpact deformation diagram

图4 300m/s时的冲击损伤云图Fig.4 Ⅰmpact damage diagram with 300m/s

图5 冲击凹坑电镜图[20]Fig.5 Electron microscope of impact pit [20]

4 单个沙粒连续冲击叶片数值模拟

4.1 有限元模型

本节利用上述方法开展单个沙粒连续冲击叶片的数值模拟研究。沙粒半径在0.3～1mm[21]，沙粒的基本力学性能见表5。考虑到飞机发动机叶片容易受到沙粒不同角度的高速冲击，因此，为了研究沙粒尺寸、冲击速度、冲击角度，以及冲击次数对叶片的冲击损伤影响，本节开展以下工况的数值模拟研究:沙粒半径分别取为0.5mm、0.7mm、0.9mm，冲击速度分别取为100m/s、150m/s、200m/s，冲击角度分别取为15°、30°、45°、60°、75°、90°，设定冲击次数为10次，见表6。冲击示意图如图6所示。叶片形状参考了参考文献[22]中叶片的基本尺寸，如图7 所示，长65mm，宽25mm，厚2mm。

图6 单个沙粒冲击示意图Fig.6 Ⅰmpact schematic diagram of single sand particle

表5 沙粒力学性能参数［23］Table 5 Mechanical property parameters of sand particles［23］

表6 单个沙粒冲击工况Table 6 Single sand impact condition

基于ABAQUS平台，建立有限元模型。在叶片冲击接触部位进行网格细化，该部分网格采用C3D8R 单元，最小网格尺寸为0.05mm。为提高计算速度，叶片非接触区域采用C3D4单元开展网格划分。考虑到沙粒的硬度远大于钛合金的硬度，在数值模拟中将沙粒视为刚体，故未考虑沙粒的率相关的特性。沙粒采用C3D8R 单元划分网格。通过有限元网格的收敛性验证分析，最终建立的有限元模型如图8所示，包含223498个单元、280486个节点。

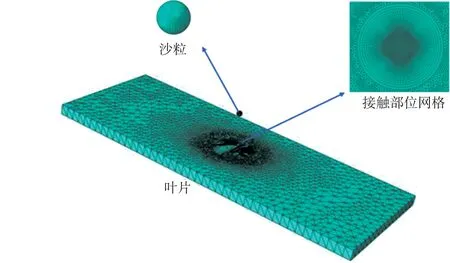
图8 单个沙粒冲击有限元模型Fig.8 Finite element model of single sand impact

4.2 单个沙粒连续冲击数值计算结果

4.2.1 冲击变形分析

为了研究单个沙粒冲击后钛合金板的变形情况，这里取沙粒半径为0.7mm，冲击速度为200m/s，冲击角度分别为30°、60°、90°的变形云图进行分析，如图9所示。可以看到，冲击角度为30°、60°时冲击局部会出现材料堆积，这是由于叶片受到了切应力，从而产生滑移，最终导致材料堆积，如图9（a）中A处和图9（b）中C处所示，同时会产生材料凹陷即冲击凹坑，如图9（a）中B处和图9（b）中D处所示；冲击角度为90°时几乎不会产生材料堆积，仅产生材料凹陷即冲击凹坑，如图9（c）所示。综上，当冲击角度小于90°时，冲击局部区域产生材料堆积和凹陷，而垂直冲击时仅产生材料凹陷。然后，分析不同角度冲击后在路径1（见图9（a）Z向）上的法向位移（U2方向）分布规律，如图9（d）所示，其中，U2＞0即为材料堆积区，U2＜0即为材料凹陷区。可以发现:冲击角度为30°时，U2 的正值最大，即材料堆积高度最大；冲击角度为90°时，U2 的负值最小，即凹陷最深。本文统一把U2＜0 的情况统称为凹坑，U2 的最小值即为凹坑的深度。图10给出了冲击凹坑深度随冲击次数的变化规律，可以看到:冲击次数越多，冲击凹坑深度越大；随着冲击次数的增加，曲线越来越平缓，表明冲击凹坑深度的变化率越来越小。图11 给出了单个沙粒一次冲击后凹坑深度随冲击速度的变化规律，可以看到，冲击速度越大，冲击凹坑深度越大。冲击凹坑深度随冲击角度的变化情况如图12所示，随着冲击角度的增加，冲击凹坑越来越深。图13给出了冲击凹坑深度随沙粒半径的变化趋势，沙粒半径越大，凹坑越深。这是由于半径越大，其质量越大，冲击动能越大，从而在沙粒与叶片接触时，叶片会吸收更多的冲击动能转化为塑性应变能，意味着更大的不可恢复的变形，在宏观上表现为更大尺寸的凹坑。

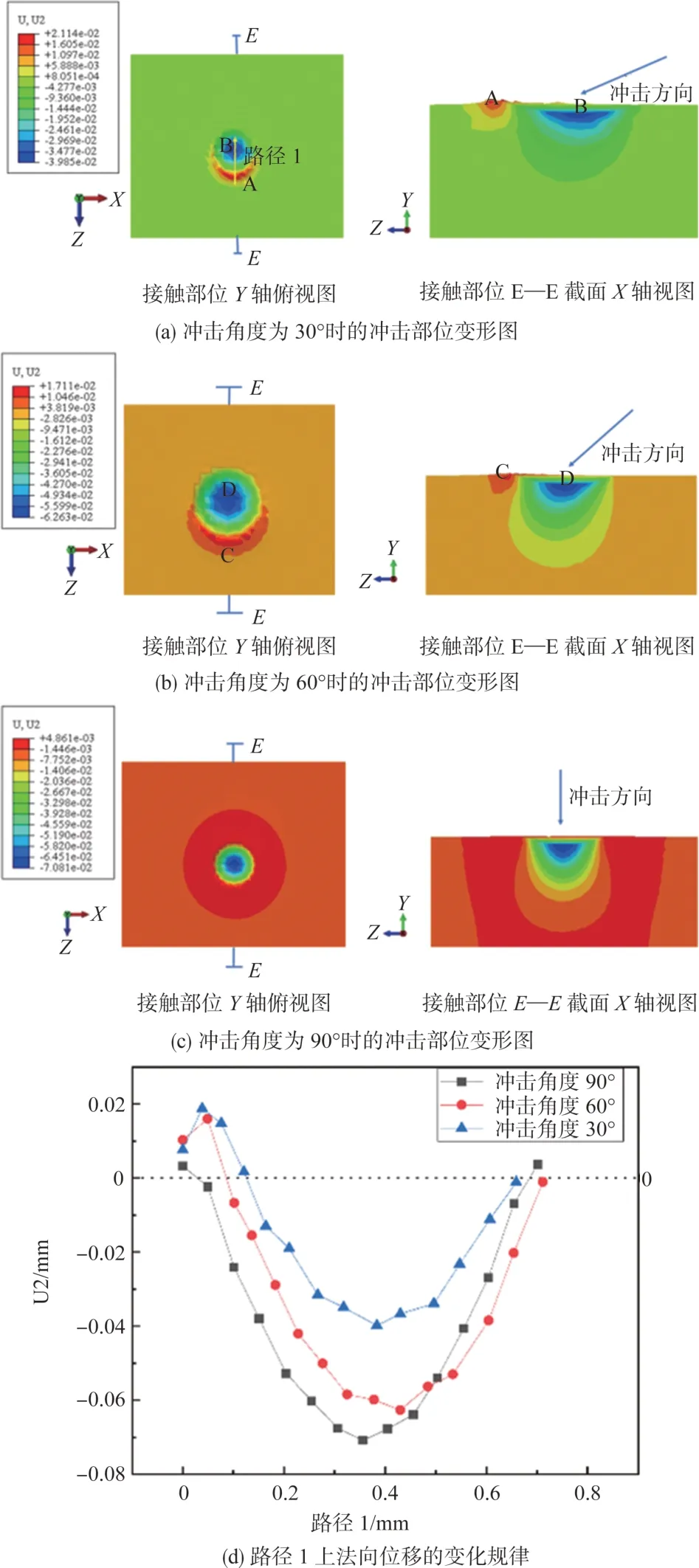
图9 不同冲击角度叶片变形情况分析Fig.9 Analysis on blade deformation at different impact angles

图10 冲击凹坑随冲击次数的变化Fig.10 Variation of impact pit with the number of impact

图11 冲击凹坑随冲击速度的变化Fig.11 Variation of impact pit with impact velocity

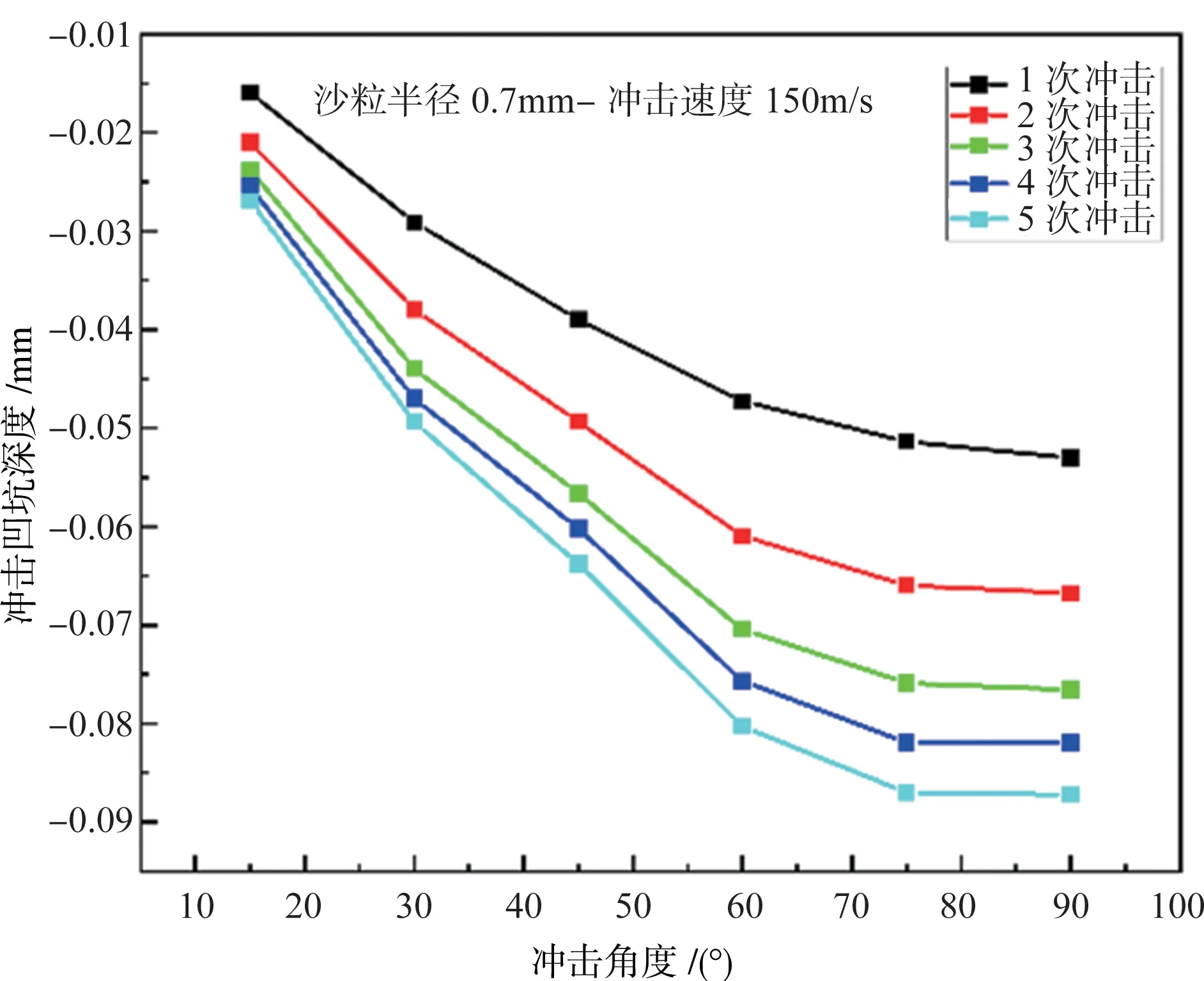
图12 冲击凹坑随冲击角度的变化Fig.12 Variation of impact pit with impact angle

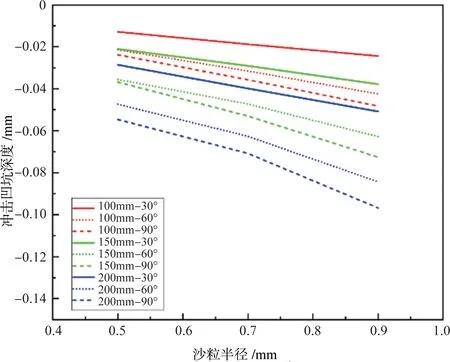
图13 冲击凹坑随沙粒尺寸的变化Fig.13 Variation of impact pit with sand particle size

4.2.2 残余应力分析

叶片受到外物冲击后，一部分冲击能量以塑性变形能的形式耗散，产生塑性变形，在受冲击区域产生较大的残余应力。本文所述的残余应力是指在移除沙粒冲击作用后，仍留在叶片内的自相平衡的内应力。本节主要分析Z方向的残余应力（S33）。图14 展示了沙粒半径为0.5mm，冲击速度为150m/s，冲击角度分别为30°、60°、90°的Z向残余应力分布云图，可以看到，冲击后产生了残余压应力和残余拉应力，且残余压应力主要出现在次表层。冲击角度为30°时，最大残余压应力值为-1308MPa，如图14（a）所示；冲击角度为60°时，最大残余压应力值为-1682MPa，如图14（b）所示；冲击角度为90°时，最大残余压应力值为-1806MPa，如图14（c）所示。对比三种情况的最大残余压应力，发现冲击角度为90°时，残余压应力最大，出现在次表层。

图15展示了图14中路径H上的残余应力分布规律，可以发现，冲击角度为90°时，残余应力在路径H 上呈现对称分布，且残余应力影响的跨度最大，而冲击角度为30°时，残余应力影响的跨度最小。图16给出了沙粒半径为0.7mm，冲击速度为150m/s，冲击角度为90°时，不同冲击次数后路径F上的残余应力分布规律，可以看到，在路径F上残余压应力先变大后变小，最后变成拉伸应力再减小趋于0。此外，一次冲击后，残余应力分布曲线基本重合，这说明一次冲击后残余应力变化率变小，但随着冲击次数的增加，残余应力影响的跨度变大。

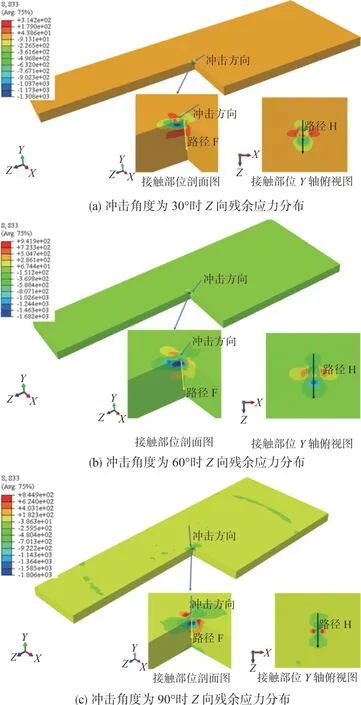
图14 不同冲击角度叶片Z向残余应力分布Fig.14 Z-direction residual stress distribution of blades ith different impact angles

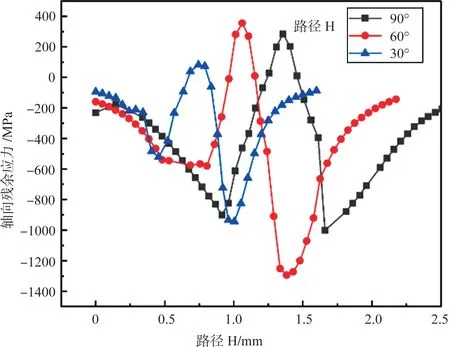
图15 不同角度冲击下路径H上的轴向残余应力分布Fig.15 Axial residual stress distribution on path H with different impact angles

图16 冲击角度为90°时，不同冲击次数下路径F上的轴向残余应力分布Fig.16 Axial residual stress distribution on path F with different number of impacts under the impact angle of 90°

为了研究残余应力与冲击速度的关系，图17给出了冲击角度为90°，沙粒半径为0.5mm，一次冲击速度分别为100m/s、150m/s、200m/s 时的路径F 上的残余应力分布曲线。可以看到，冲击速度越大，曲线越靠下且曲线跨度越大，即接触部位产生的整体残余压应力越大且残余应力影响跨度越大。图18 给出了不同沙粒半径对残余应力的影响，发现沙粒半径越大，残余压应力越大且残余应力影响跨度越大。

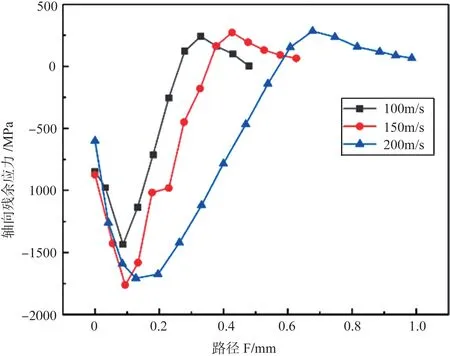
图17 不同冲击速度下路径F的轴向残余应力分布Fig. 17 Axial residual stress distribution on path F with different impact speeds

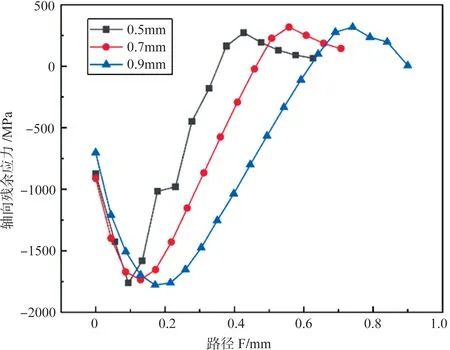
图18 不同沙粒半径下路径F的轴向残余应力分布Fig. 18 Axial residual stress distribution on path F with different sand radius

4.2.3 冲击损伤分析

本节所述的冲击损伤是由损伤度D 表征，基于前述的冲击损伤模型，可计算沙尘颗粒一次冲击所产生的损伤增量，可以得到单个沙粒在不同冲击角度（30°、60°及90°）下的冲击损伤分布云图。如图19 所示，可以看到，当冲击角度为30°时，最大损伤出现在叶片表面，这是由于当冲击角度为30°时，会产生切削作用。图20 展示了沙粒半径为0.7mm，冲击速度为200m/s，且同一次冲击后，冲击损伤最大值随着冲击次数的变化规律，可以发现，冲击次数越多，冲击损伤最大值越大，但随着冲击次数的增加，冲击损伤最大值的变化率越来越小，这是由于冲击在产生损伤的同时也会使材料得到硬化，这种硬化减缓了冲击损伤的增加。图21给出了冲击损伤与冲击速度的关系，从图21中可以看出，冲击速度越大，冲击损伤越大。图22 给出了沙粒半径为0.9mm、冲击速度为150m/s情况下，不同冲击角度下冲击损伤的变化规律，可以看出冲击损伤在30°时最大。图23展示了冲击速度为200m/s、冲击角度为90°时，不同沙粒尺寸造成的冲击损伤随冲击次数的变化规律，可以发现，沙粒半径越大，产生的损伤越大。

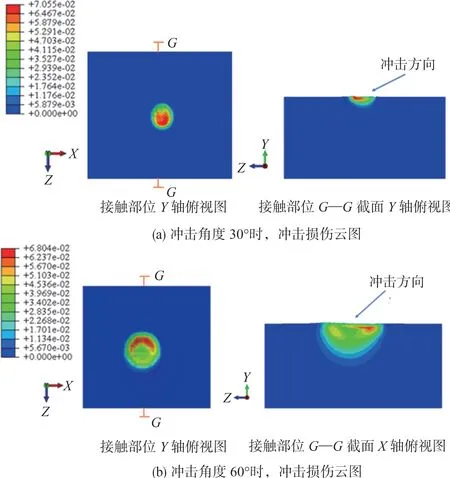
图19 不同冲击角度损伤分布Fig.19 Damage distribution at different impact angles

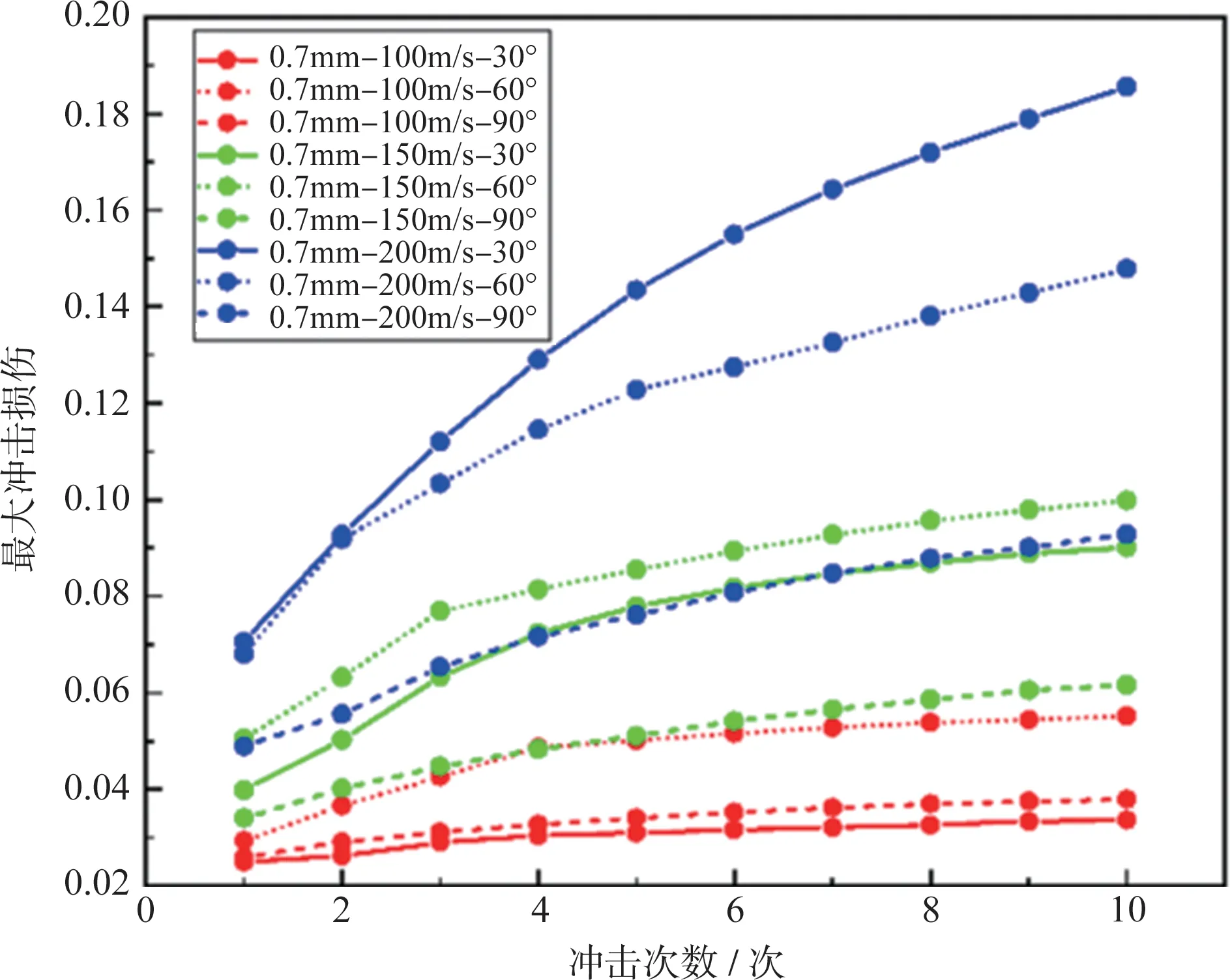
图20 不同冲击次数下最大损伤变化规律Fig.20 Variation of maximum damage versus different number of impacts

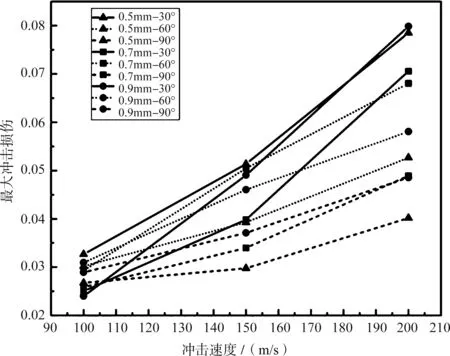
图21 不同冲击速度下最大损伤变化规律Fig. 21 Variation of maximum damage versus different impact speeds

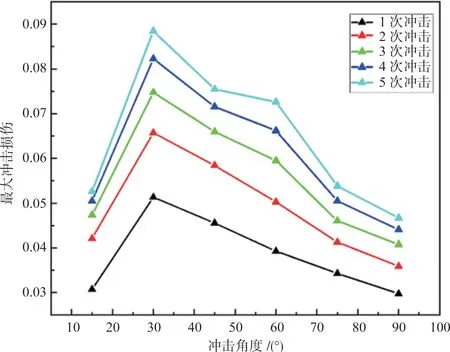
图22 不同冲击角度下最大损伤变化规律Fig.22 Variation of maximum damage versus different impact angles

图23 不同沙粒尺寸下最大损伤变化规律Fig.23 Variation of maximum damage versus different sand particle size

5 多个沙粒连续冲击叶片数值模拟分析

5.1 有限元模型

在沙漠环境中，叶片会同时受到多个沙粒的冲击作用，本节开展多个沙粒连续冲击叶片的数值模拟分析，研究冲击损伤与沙粒个数及冲击位置的关系。为了更加真实有效地模拟多个沙粒的冲击作用，这里考虑沙粒冲击位置的随机分布。设置沙粒个数分别为10个、20个、30个、40个，同时考虑沙粒冲击时冲击位置的随机性，分两种情况，即第一次冲击位置随机后不变和每次冲击位置都随机。沙粒冲击速度为150m/s，沙粒半径为0.5mm，冲击角度为90°，计算模拟工况见表7。多个沙粒冲击示意图如图24所示。

表7 多个沙粒冲击工况说明Table 7 Impact conditions of multiple sand

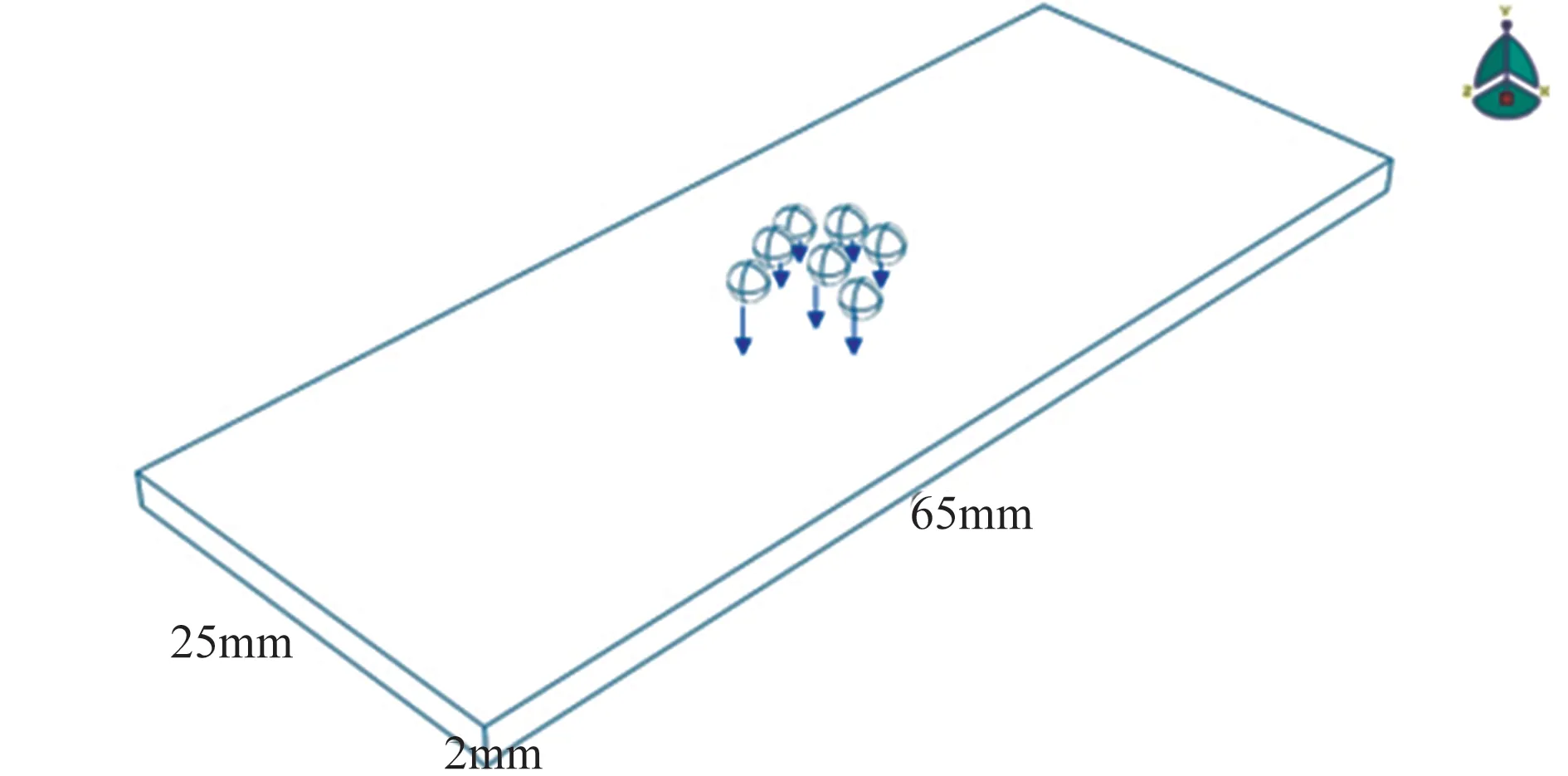
图24 多个沙粒冲击示意图Fig.24 Schematic diagram of multiple sand impact

建立多个沙粒冲击的有限元模型如图25 所示，采用C3D8R 单元，在主要接触部位细化网格，通过有限元网格的收敛性验证分析，最终，该模型共包含280097 个单元、387838个节点，最小单元尺寸为0.05mm。模型的边界条件为一端固支，沙粒与钛合金板之间设为通用接触，摩擦系数为0.15。为保证沙粒与叶片冲击后完全分离，本文设置的时间间隔为10-5s。

图25 多个沙粒冲击的有限元模型图Fig.25 Finite element models of multiple sand impact

5.2 多个沙粒连续冲击数值计算结果

5.2.1 冲击变形分析

对于两种不同的随机冲击方式，30个沙粒连续冲击10次后的变形云图如图26 所示。图27 给出了两种不同随机冲击方式冲击下，最大冲击凹坑深度与沙粒个数、冲击次数的变化规律，红线代表每次冲击位置随机的情况，蓝线代表第一次冲击位置随机后不变的情况。可以发现，沙粒个数越多，最大冲击凹坑深度越深，且随着冲击次数增加，冲击凹坑深度越大，与此同时，最大凹坑深度的变化率也增大。对比这两种不同的冲击位置随机分布情况，可以看到，红线均位于蓝线下方，且红线比蓝线更加陡峭，这说明每次冲击位置随机的冲击方式产生的最大冲击凹坑深度更深，可以推断随机冲击会减弱冲击后的硬化作用。

图26 30个沙粒连续冲击10次后变形云图Fig.26 Deformation diagram after 10 consecutive impacts of 30 sand particles

图27 最大凹坑深度与沙粒个数和冲击次数的关系Fig.27 Relationship between the maximum pit depth and the number of sand particles and impact times

5.2.2 冲击损伤分析

对于两种不同的随机冲击方式，30个沙粒连续冲击10次后所造成的冲击损伤云图如图28 所示，可以发现，冲击损伤主要发生在沙粒与叶片接触部位。图29 给出了两种不同随机冲击方式冲击下，最大冲击损伤与沙粒个数、冲击次数的变化规律。红线代表每次冲击位置随机的情况，蓝线代表第一次冲击位置随机后不变的情况。可以看到，对于蓝线，沙粒个数越多，最大冲击损伤越大，且第二次冲击之后，不同沙粒个数的最大冲击损伤有明显差异，与此同时，这种差异随着冲击次数的增加而增加；对于红线，冲击损伤随冲击次数变化呈阶段性突增，且沙粒个数为20 个、30 个、40 个时，每次冲击位置随机的冲击方式造成的损伤大于第一次冲击位置随机后不变的冲击方式，这说明随机冲击会减弱强化作用，更容易造成冲击损伤。

图28 30个沙粒连续10次冲击后冲击损伤云图Fig.28 Ⅰmpact damage diagram after 10 consecutive impacts of 30 sand particles

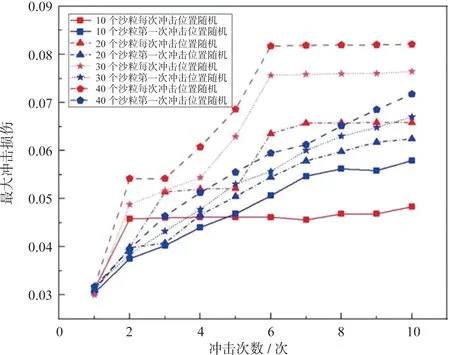
图29 最大冲击损伤与沙粒个数和冲击次数的关系Fig.29 Relationship between the maximum impact damage and the number of sand particles and impact times

6 结论

本文建立了毫米级球状沙尘颗粒连续冲击损伤的力学模型与数值模拟方法，并以钛合金叶片为例，进行了单个及多个沙粒连续冲击的变形、残余应力及损伤分析。主要结论如下:

（1）基于ABAQUS 平台，通过编写Vufield 子程序和Python 脚本，实现了连续冲击损伤计算的数值模拟。通过将计算结果与参考文献中的试验数据进行对比，验证了该方法的有效性。

（2）基于建立的连续冲击模拟方法，开展了单个沙粒连续冲击叶片数值模拟分析。冲击凹坑深度、冲击残余应力的影响跨度及冲击损伤最大值与沙粒尺寸、冲击速度、冲击次数成正相关。冲击角度为30°时，冲击损伤最大。此外，随着冲击次数的增加，冲击凹坑深度、残余应力跨度和冲击损伤的变化率减小，主要是由于前一次冲击会对材料局部产生一定的硬化作用，进而减缓冲击损伤增加的速率。

（3）针对两种不同的随机冲击方式，即每次冲击位置随机情况和第一次冲击位置随机后不变的情况，开展了多个沙粒连续冲击叶片的数值模拟分析。沙粒个数越多，最大冲击凹坑深度越深，且随着冲击次数增加，冲击凹坑深度越大，与此同时，最大凹坑深度的变化率也增大。此外，冲击损伤主要发生在沙粒与叶片接触部位。冲击损伤随冲击次数变化呈阶段性突增，每次冲击位置随机的冲击方式造成的损伤大于第一次冲击位置随机后不变的冲击方式。