支持无人机设计的全寿命周期成本建模技术研究

缪炜星，冯欢欢，简铭，张海涛

1.中航（成都）无人机系统股份有限公司，四川 成都 611000

2.中国航空工业发展研究中心，北京 100029

无人机是一种典型的技术高度复杂、研制周期长的航空产品，我国无人机研制更加倾向于飞行性能、重量（质量）以及研制的进度，往往忽略了经济性的影响，或者仅仅考虑其研制生产及采购成本，在成本分析评价和管理等方面，我国的工作起步较晚。

随着无人机应用先进的材料、航电和任务设备以及采用先进的制造技术，其购买使用成本快速增长，研发综合性能更高、成本更低的无人机，对提高其市场竞争力有重要的意义。

因此，在无人机设计阶段对相关成本进行分析评估，引入按费用设计理念，对于控制无人机装备指标参数与复杂程度、鉴别高费用设计、修正设计进程、提高标准化程度，进而降低全寿命周期费用，实现技术与经济的最佳匹配，达到最优效费比，将起到极其重要的作用[1]。

无人机的经济性通常用全寿命周期成本来衡量。按照美国国防部的定义，可以将无人机的全寿命周期成本定义为获得无人机以及使用所产生的所有成本，包括设计研发、生产制造、使用维护和报废等成本。美军2020 年9 月最新研究表明[2]:在无人机全寿命周期成本中，研制费占12%，采购费占27%，使用费占58%，其他成本占3%。在设计阶段，无人机所消耗的成本较低，但是已经决定了85%的全寿命周期成本；在生产制造阶段初期，更是决定了95%的全寿命周期成本，在制造结束，其全寿命周期成本已经基本确定。

当前，大多数成本模型关注的是某个特定的成本要素，而不是整体的成本架构。同样，建模是针对特定阶段的，而不是全寿命周期的。成本模型应该显示对设计影响最大的变量和参数，以便在可替代产品之间进行多学科分析或权衡研究比较。

无人机成本估算在航空领域中已广泛应用多年，但仍需进一步研究:（1）成本模型应该是完整和通用的，可以追溯到产品描述中的驱动元素；（2）成本模型需要与产品定义相联系，以便产品细节的任何变化都反映在成本模型中；（3）为了使成本模型具有相关性，需要将其与设计工具相结合，从而形成一个设计决策支持工具；（4）为了预测成本估算的不确定性及其原因，应将统计分析与成本估算相结合，并利用可视化工具来构建；（5）成本模型必须易于理解和访问，有助于设计师在早期阶段对设计进行修改以降低成本[3]。

本文分析了一种无人机全寿命周期成本估算框架，研究了无人机全寿命周期成本体系架构，提出了无人机飞机平台全寿命周期成本估算模型，将该模型在某型无人机上进行验证，可以用于无人机研制过程中的设计方案权衡分析和基于成本的设计优化。

1 无人机全寿命周期成本估算框架

本文开发的框架通过将产品定义作为成本模型的输入，能够估算任何给定无人机的成本，设计中的主要变化都反映在成本模型中[4]。无人机产品定义大致可以分为显性产品定义和隐性产品定义。显性产品定义包括几何参数（设计尺寸）、重量、材料类型、动力装置等[5]。例如，设计尺寸的改变会导致原材料和制造成本的改变。隐性产品定义指的是对成本影响不容易识别的设计参数，包括航程、作战半径、巡航和最大速度、机动性、故障模式影响及危害性技术数据等。如飞机最大速度、战斗损伤取决于飞机速度，更高的速度意味着被击中的概率更低，维修成本也随之降低[6]。在本文中，所有这些特征都被纳入估算无人机全寿命周期成本的框架中，如图1所示。

图1 全寿命周期成本框架Fig.1 Life cycle cost framework

从全寿命周期成本分析对应的成本类型来说，主要包括研制成本、生产成本、使用保障成本、退役处置成本4类[7]。一般情况下，退役的军用飞机最后要封存起来，成本占比不高，通常在军机全寿命周期成本分析中可忽略不计，本文在研究整机级成本模型所对应的成本类型时仅包括研制成本、生产成本、使用保障成本，分解结构如图2所示。

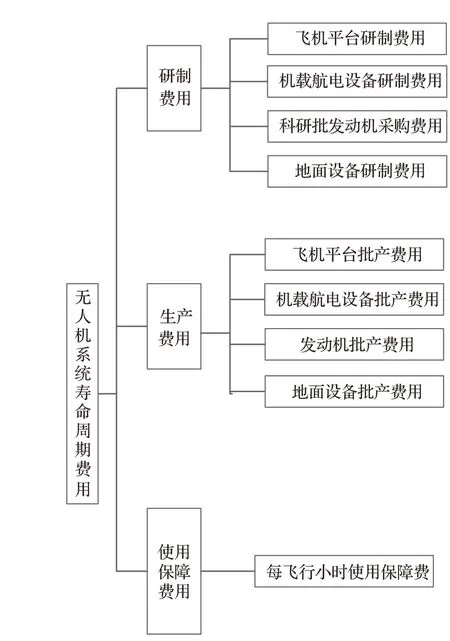
图2 无人机系统整机级成本分解结构Fig.2 Cost breakdown structure of UAV system

2 无人机全寿命周期成本估算方法

本文为了构建便捷快速的无人机全寿命周期成本估算模型，主要从建模方法、数据收集等方面进行深入研究。一方面，考虑样本数量的不足以及部分参数数据的缺失，采用偏最小二乘方法构建无人机全寿命周期成本模型[8]；另一方面，收集的数据包含美国大、中、小三个档次的无人机相关数据，为国内开展相关无人机低成本设计提供重要数据支持。

2.1 样本数据与模型结构

收集的无人机数据时间跨度大，性能范围宽，空重为0.38～20883kg，续航时间为1～32h，作战半径为2.96～10000km，实用升限为304～19760km。基本反映了美国无人机研制、生产的全貌，型号数据收集达到25 个无人机型号，包括MQ-1、RQ-2、RQ-4、MQ-5、RQ-7、RQ-8、MQ-9、X-45C、X-47B等。

无人机全寿命周期成本的影响参数主要考虑了长度（m）、翼展（m）、空重（kg）、油载（kg）、载重（kg）、续航时间（h）、作战半径（km）、实用升限（m）、最大航速（km/h）、巡航速度（km/h）等。

由于数据收集确实存在难度，无人机并非都具有非常完整的技术经济信息，用于成本模型的构建。从总体数据的层面来说，有个别型号的技术参数是缺失的，但基本上可以满足建模的需要。

2.2 估算模型结构

参数方程的结构直接影响到预测模型的精度和预测未来无人机成本的准确性。在兰德公司的“飞机研制成本及采购成本估算的计算模型”[9]和我国“飞机全寿命成本分析”科研报告中，统一取参数方程的结构为

lnY=a0+a1lnx1+a2lnx2+…

式中，Y为成本元素；x1，x2，…为发动机性能参数；a0，a1，a2，…为由回归分析确定的系数。称这种形式的参数方程为全部参数对数方程。这种参数方程的结构基于成本元素和性能参数的无量纲化。

考虑到我国无人机技术经济数据的自然规律以及偏最小二乘回归的特点和原理，本文采用的参数方程为全部参数对数方程。

2.3 模型的建立

2.3.1 研制成本估算模型

基于收集的无人机研制成本、物理和技术参数，对数据进行相关性分析，分析结果见表1。从表1中可知，将长度、翼展、空重、油载、载重、续航时间、实用升限和最大航速8个参数作为自变量，选取自变量标准是自变量与研制成本相关性系数大于0.5。

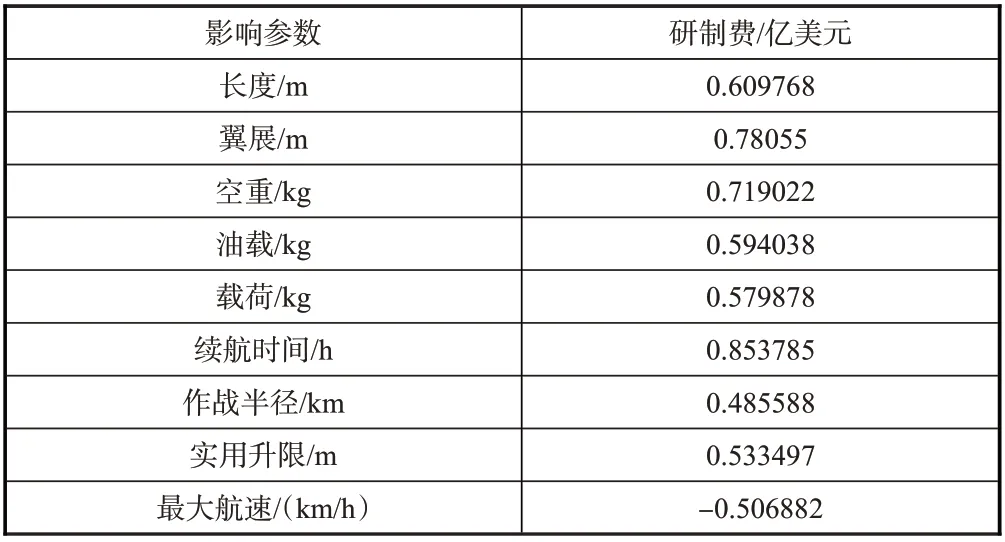
表1 研制成本自变量相关关系表（2019年）Table 1 Development cost independent variable correlation table（2019）

根据历史型号样本点数据最大航速与研制费呈现负相关，即最大航速越大，研制费越小，这个主要由于研制费是受多个参数综合影响，不是由单一参数影响决定的，如续航时间，翼展等影响较大，如果用单一参数来评估研制费，有时反应出的规律可能会与认知相反结果。因此，一般使用多参数进行经济性评估，不使用单个参数进行经济性评估。

系统根据交叉有效性指标，选择一个偏最小二乘成分，得到最佳的偏最小二乘回归模型。图3给出累计解释能力与交叉有效性。

图3 研制成本模型自动拟合Fig.3 Automatic fitting of development cost model

以各说明性变量为自变量，研制成本为因变量，偏最小二乘回归提取两个主成分t1和t2。计算t1和t2的方差，取置信度为95%，在t1、t2平面上作出椭圆图，如图4所示。

从图4中可以看出，样本点分布在椭圆内，不存在特异点。因此，模型的拟合效果是好的，不需要做改动。模型拟合参数见表2。从表2中可以看出，模型对无人机研制成本的解释能力为0.928，精度满足工程使用要求。

表2 研制成本模型拟合效果参数Table 2 Fitting effect parameters of development cost model

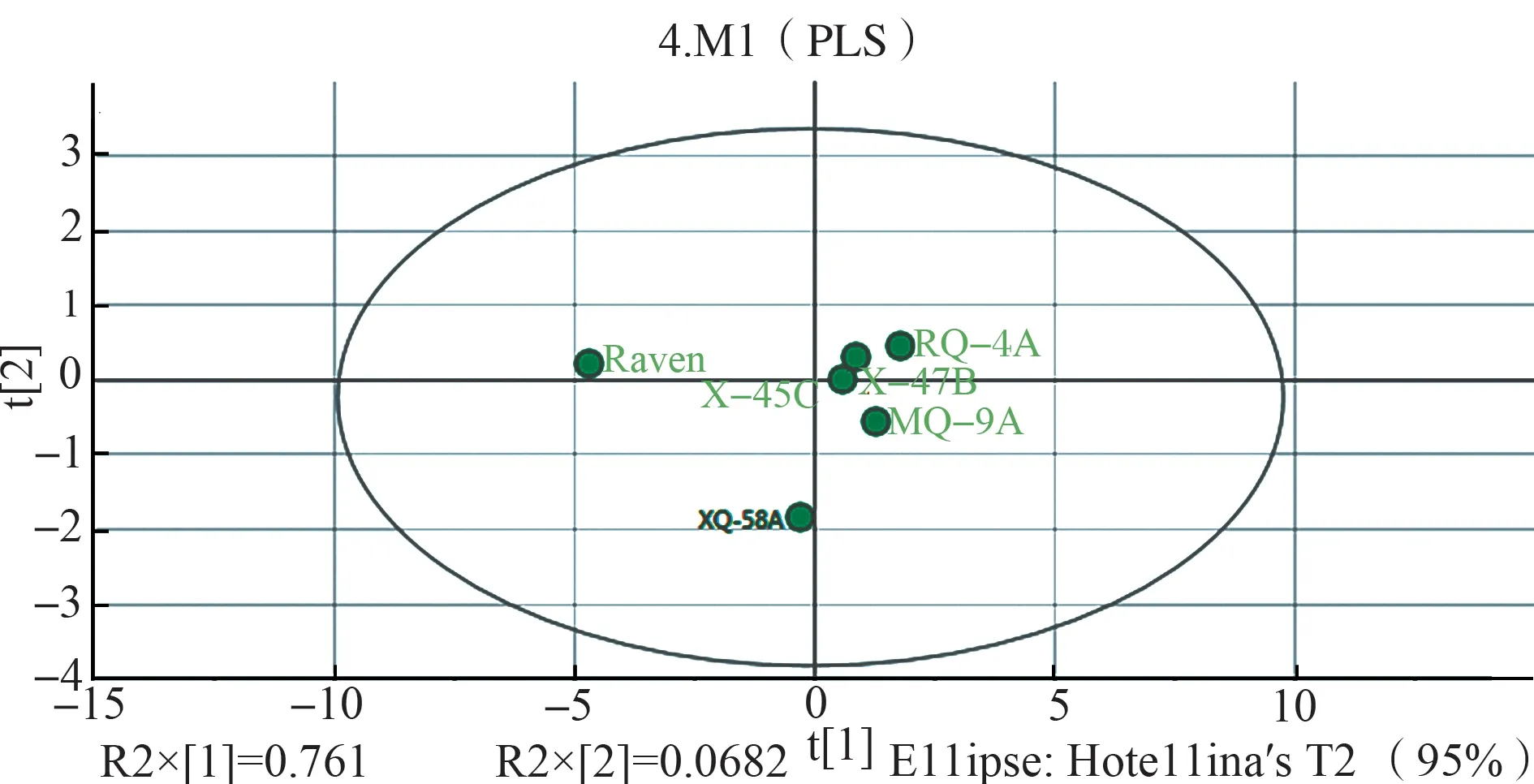
图4 研制成本样本筛选椭圆图Fig.4 Development cost sample screening ellipse

无人机研制成本与8个自变量的标准化偏最小二乘回归模型为

Log10(cost)=-a0+a1×Log10(X1)+a2×Log10(X2)+a3×Log10(X3)+a4×Log10(X4) +a5×Log10(X5)+a6×Log10(X6) -a7×Log10(X7)-a8×10Log10(X8)式中，cost为研制成本（亿元）；X1为长度；X2为翼展；X3为空重；X4为油载；X5为载重；X6为续航时间；X7为实用升限；X8为最大航速；a0～a8为常系数。

为了更直观地观测自变量解释生产成本的作用，可以绘制回归系数图，如图5所示。图5是针对标准化数据的回归方程系数。

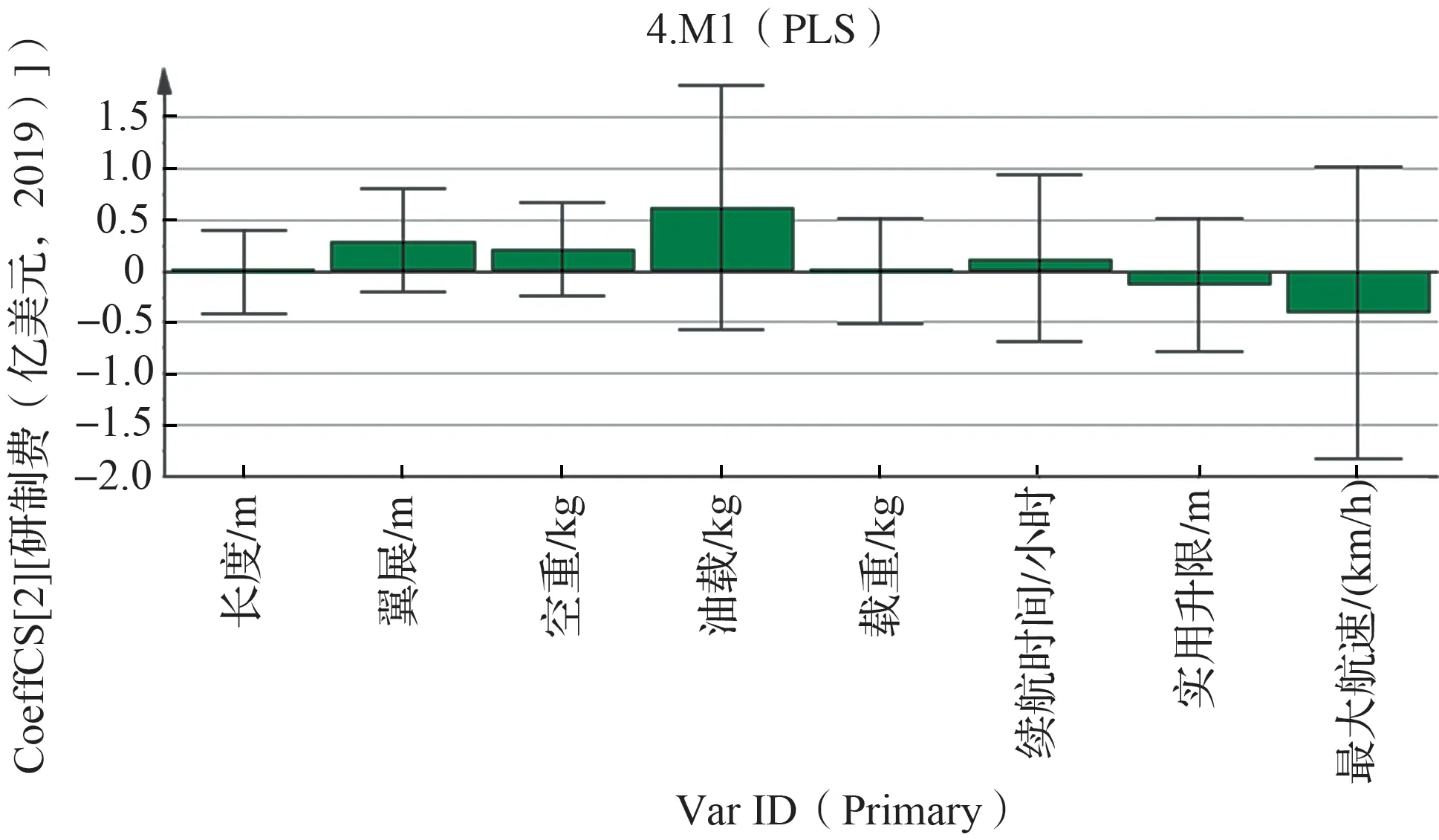
图5 研制成本模型回归系数图Fig.5 Regression coefficient diagram of development cost model

2.3.2 生产成本估算模型

基于收集的无人机生产成本、物理和技术参数，对数据进行相关性分析，分析结果见表3，从表3 中可知，将长度、翼展、空重、油载、载重、续航时间、作战半径、实用升限、最大航速和巡航速度10个参数作为自变量，选取自变量标准是自变量与生产成本相关性系数大于0.5。

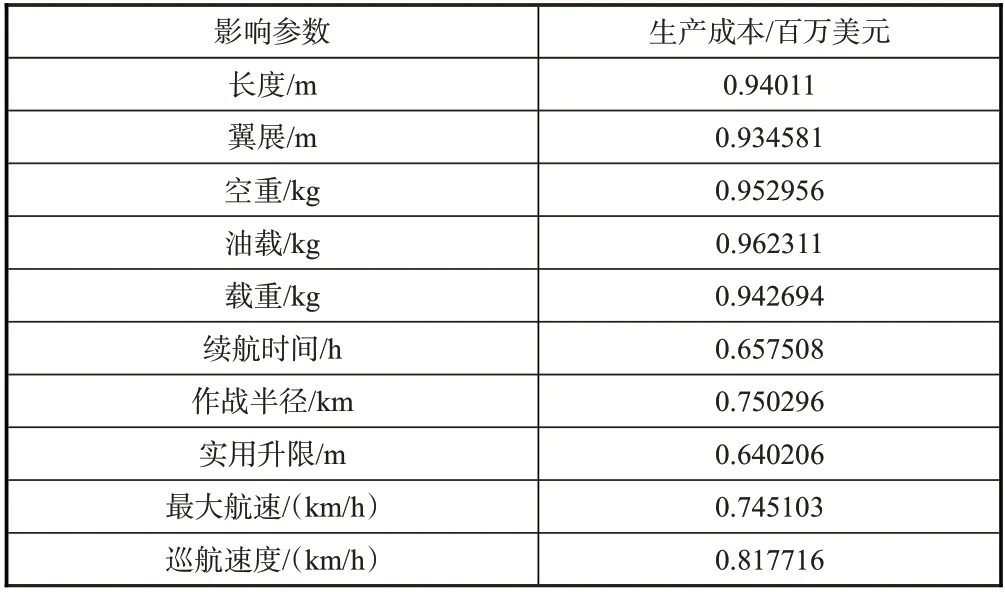
表3 生产成本自变量相关关系表（2019年）Table 3 Correlation table of independent variables of production cost（2019）

系统根据交叉有效性指标，选择一个偏最小二乘成分，得到最佳的偏最小二乘回归模型。图6给出累计解释能力与交叉有效性。

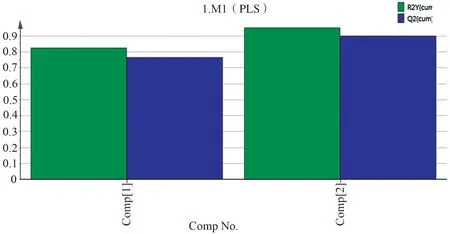
图6 生产成本模型自动拟合Fig.6 Automatic fitting of production cost model

以各说明性变量为自变量，单机成本为因变量，偏最小二乘回归提取两个主成分t1和t2。计算t1和t2的方差，取置信度为95%，在t1、t2平面上作出椭圆图，如图7所示。

图7 生产成本样本筛选椭圆图Fig.7 Production cost sample screening ellipse

从图7中可以看出，样本点分布在椭圆内，不存在特异点。因此，模型的拟合效果是好的，不需要做改动。模型拟合参数见表4。

从表4 中可以看出，模型对无人机生产成本的解释能力为0.953，精度满足工程使用要求。

表4 生产成本模型拟合效果参数Table 4 Fitting effect parameters of production cost model

无人机生产成本与10 个自变量的标准化偏最小二乘回归模型为

式中，cost为生产成本（亿元）；X1为长度；X2为翼展；X3为空重；X4为油载；X5为载重；X6为续航时间；X7为作战半径；X8为实用升限；X9为最大航速；X10为巡航速度；a0～a10为常系数。

为了更直观地观测自变量解释生产费用的作用，可以绘制回归系数图，如图8所示。图8是针对标准化数据的回归方程系数。

图8 生产成本模型回归系数图Fig.8 Regression coefficient diagram of production cost model

2.3.3 使用保障成本估算模型

基于收集的无人机使用保障成本、物理和技术参数，对数据进行相关性分析，分析结果见表5。从表5 中可知，将长度、空重、油载、载重、作战半径、实用升限、最大航速和巡航速度8 个参数作为自变量，选取自变量标准是自变量与使用保障成本相关性系数大于0.5。

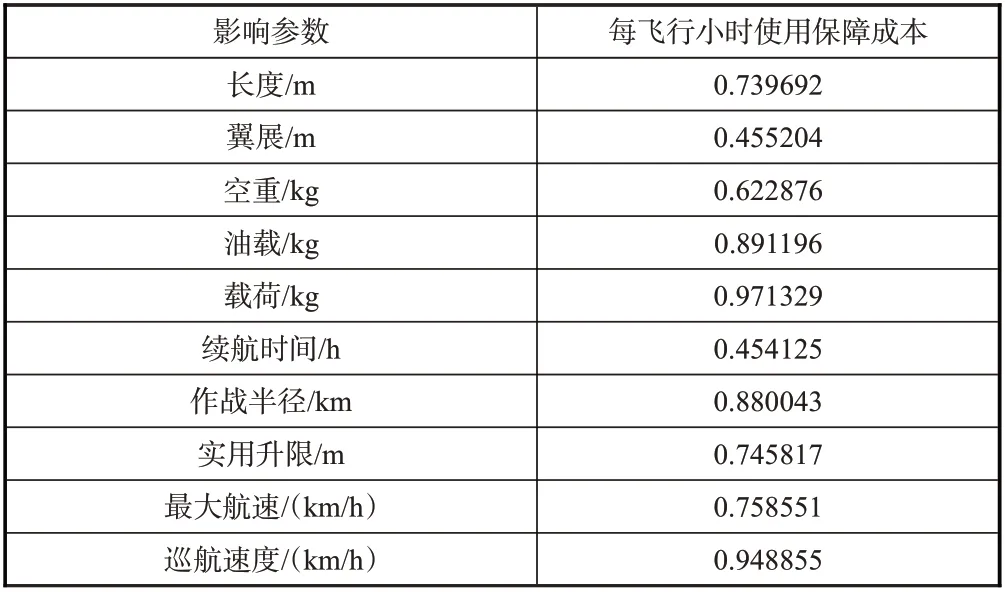
表5 使用保障成本自变量相关关系表（2019年）Table 5 Correlation table of independent variables of operating and support cost（2019）

系统根据交叉有效性指标，选择一个偏最小二乘成分，得到最佳的偏最小二乘回归模型。图9给出累计解释能力与交叉有效性。模型拟合参数见表6。从表6可以看出，模型对无人机使用保障费用的解释能力为0.776，精度满足工程使用要求。

表6 使用保障成本模型拟合效果参数Table 6 Operating and support cost model to fit the effect parameters

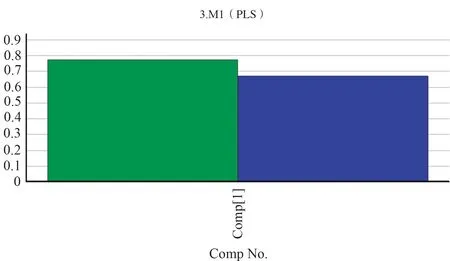
图9 使用保障成本模型自动拟合Fig.9 Automatic fitting operating and support cost model

无人机使用保障成本与8个自变量的标准化偏最小二乘回归模型为

Log10(cost)=-a0+a1×Log10(X1)+a2×Log10(X2)+a3×Log10(X3)+ a4×Log10(X4)+ a5×Log10(X5)+ a6×Log10(X6)+ a7×Log10(X7)+ a8×Log10(X8)

式中，cost 为每飞行小时使用保障成本；X1为长度；X2为空重；X3为油载；X4为载重；X5为作战半径；X6为实用升限；X7为最大航速；X8为巡航速度；a0～a8为常系数。

为了更直观地观测自变量解释使用保障成本的作用，可以绘制回归系数图，如图10所示。图10是针对标准化数据的回归方程系数。

图10 使用保障成本模型回归系数Fig.10 Regression coefficient diagram of operating and support cost model

3 案例验证

本文选取某型无人机两种概念设计方案进行全寿命周期成本估算模型验证。该型无人机翼展15m，机长9m，机高2m。两种设计方案因复合材料占结构重量比重的不同（方案1 为60%、方案2 为80%），导致技术性能参数略有不同[10]。

验证结果表明，方案2 的研制与生产成本高于方案1，主要原因是复合材料的原材料和制造成本高；方案2 的使用保障成本高于方案1，主要原因是金属材料涉及的修理成本和燃料消耗较高。

按照30年寿命周期、10架机队规模对模型进行了仿真模拟，估算两种方案机队全寿命周期成本，如图11 所示。两种方案的全寿命周期成本差异也随时间变化，在最初几年，方案2的成本超过方案1的成本，但从长远来看，方案2的成本要低于方案1，主要原因是方案2的使用保障成本远远低于方案1。

图11 全寿命周期成本对比Fig.11 Life cycle cost comparison

4 结论

本文构建了无人机全寿命周期成本估算框架，建立了全寿命周期成本估算模型，经在某型无人机上应用验证，表明可用于无人机设计阶段的成本方案权衡研究、多学科分析与优化。

当前的研究仍存在不足，也是未来的研究方向。一是采购成本知识库可以进一步改进，包括更多的材料，制造过程和结构库，可以估计不合格（报废和返工）成本，这将有助于设计师通过适当选择设计尺寸、公差和材料来降低不合格成本；二是使用保障成本模型可以扩展到更多的任务和不同的飞机，将不同的维修模式集成到仿真模型中，通过蒙特卡罗模拟进行的不确定性分析和大型模型的成本敏感性分析，检验其对使用保障成本的影响；三是开发可视化系统，部署在安全的Web服务器上，在行业内部共享，实现成本计算Web 服务与CAD 模型、CFD 分析和有限元模型集成。