基于迭代反馈调参的伞翼飞行器无模型自适应控制方法研究

赵令公，贺卫亮，赵志高，刘志君

1.中国航空研究院，北京 100012

2.北京航空航天大学，北京 100191

伞翼飞行器是一种柔性翼飞行器，成本低、应用面广、安全性高、机动灵活，满足未来航空发展的低成本及分布式新质装备发展需求[1]。其主要包含伞翼、伞绳、载荷和控制系统等部分。冲压的柔性伞翼在飞行过程中保持一定的刚度，为飞行器提供气动力，伞绳连接伞翼和有效载荷；控制系统包含舵机、传感器和控制计算机，控制计算机基于传感器和舵机信息计算、输出控制指令。控制系统是伞翼飞行器可控飞行的至关重要部分。但是由于受柔性伞翼和伞绳的影响，伞翼飞行器系统具有强非线性，因此，无法构建精确的动力学模型，也就无法通过基于模型的设计方法来设计其控制系统。本文采用基于数据驱动的控制器设计方法，摆脱了控制器设计过程中对精确动力学模型的依赖。

控制系统通过对称或不对称下拉伞翼左右后缘控制绳，实现伞翼飞行器纵向和横侧向控制[2]，以完成对指定路径的跟踪和精确空投。伞翼飞行器具有普通降落伞减少着陆冲击和可控飞行的能力，因此，近几十年来一直被用来提高物资投放精度[3]。已有数十种精确空投系统被用来测试，以满足不同的应用需求[4]。

作为柔性翼飞行器，伞翼飞行器与固定翼飞行器有较大的区别。伞翼飞行器的柔性伞翼部分在扰动时易发生结构变形，如突风及控制输入，而这种变形会影响气动力且在仿真中无法精确描述。另外，伞绳有时处于非张紧状态，影响伞翼和载荷之间力的传递，导致系统不稳定。并且，在实际飞行过程中，伞翼飞行器的控制输入由舵机来实现，舵机的响应时间会有变化，因此，控制器需要在飞行过程中实时进行调整。

上述多种因素导致伞翼飞行器的动力学仿真与实际情况有较大差距。柔性伞翼和松弛状态下的伞绳引起伞翼飞行器系统模型的不准确，也使系统模型中的力学关系不准确。因此，基于模型建立的控制系统在本飞行器中与实际情况相差较大，且控制参数需要在每次飞行过程中进行自适应调节。

一些专家学者和研究机构致力于解决伞翼飞行器上述问题。Yakimenko 主持编写了《精确空投系统:建模、动力学和控制》，详细介绍伞翼飞行器各个方面的内容，如冲压翼伞分析、着陆精度影响分析、动力学和控制分析[4]。Sun Qinglin和Sun Hao 采用改进型PⅠD 控制方法，通过线性扩展状态观测器的方式，增加传统PⅠD控制器的鲁棒性[5]。Carter等采用前馈方法提高PⅠD控制器的响应时间，并利用半物理仿真飞行试验验证了该控制器的可用性[6]。Tao Jin和Sun Qinglin使用主动抗干扰方法控制伞翼飞行器精确跟踪预定轨迹，通过扰动测量方法避免了对动力学方程精度的要求，比较适用于伞翼飞行器这种强非线性系统[7-8]。

上述控制方法基本上都不依赖于精确的伞翼飞行器动力学模型，并且在每次仿真或飞行测试中，控制器都会随之发生变化。因此，不基于模型的控制方法，可以解决强非线性系统的部分问题。对其他相关的非线性系统的研究也在进行中。采用自适应逆方案和状态反馈控制的自适应拟阵列控制方法，对于不确定性扰动具有较好的鲁棒性；采用自适应积分反步控制方案对直升机进行控制，通过对参数和模型不确定性的估计，提高参数不确定性和未建模动态情况下的系统鲁棒性[9]。其他非线性系统的控制问题，如非线性开关系统[10-11]、基于信号的执行机构的非线性[12]、微生物燃料电池[13]、糖尿病患者的血糖[14]、鲁棒容错H∞控制[15]等也已经在研究中。

本文采用基于迭代反馈调参的无模型自适应控制方法设计伞翼飞行器的控制系统，利用输入、输出数据对控制器参数进行调参。ⅠFT-MFAC是伞翼飞行器的非线性问题的一种解决方案，利用ⅠFT 方法对MFAC 控制方法的两个步长因子进行调参，并通过仿真验证ⅠFT-MFAC 控制器的控制效果。首先，简单介绍了伞翼飞行器动力学建模，该模型不参与控制器的设计，仅用于控制效果的验证；其次，推导了ⅠFTMFAC控制方法的构建过程，并通过仿真验证该方法对伞翼飞行器控制的有效性。仿真中共设置两种轨迹和三种状态，对ⅠFT-MFAC 控制器的控制效果与PⅠD 控制器、ADRC 控制器和MFAC 控制器进行对比。多个控制方法均可为伞翼飞行器的非线性问题提供解决方案，但是ⅠFT-MFAC控制器的控制输入值较小，也就意味着较少的能量消耗。

1 伞翼飞行器动力学模型

1.1 基本假设

伞翼飞行器六自由度动力学模型可以满足其对预设轨迹的跟踪效果的分析需求，因此，构建六自由度动力学模型，基本假设如下:（1） 伞翼飞行器作为一个刚性整体，伞翼和载荷舱之间不存在相对运动；（2） 伞翼在飞行过程中保持刚性，忽略结构变形引起的气动力和力矩变化；（3） 伞翼飞行器系统沿展向对称；（4）柔性伞翼的质心位于1/4弦线处；（5）忽略伞绳和吊带的质量和气动力；（6）平面大地假设。

1.2 坐标系定义

在构建伞翼飞行器六自由度动力学模型时，需要用到三个基本坐标系:大地坐标系{i}、飞行器本体坐标系{b}和气流坐标系{a}。

伞翼飞行器本体坐标系和大地坐标系之间的关系由三个欧拉角表示，即滚转角φ、俯仰角θ和偏航角ψ。两个坐标系之间的转换由转换矩阵表示

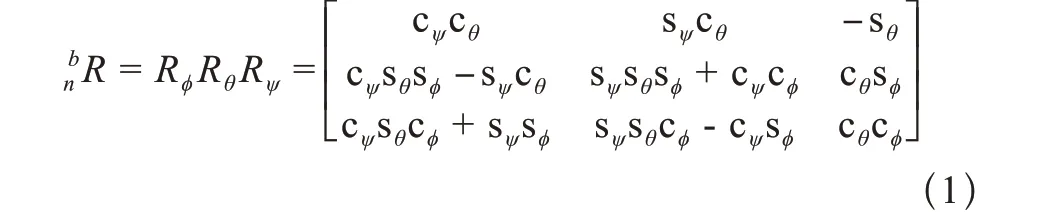
式中，cx和sx代表三角函数cosx和sinx，x指代欧拉角。

伞翼飞行器本体坐标系与气流坐标系之间的关系由两个角度决定，即迎角α和侧滑角β

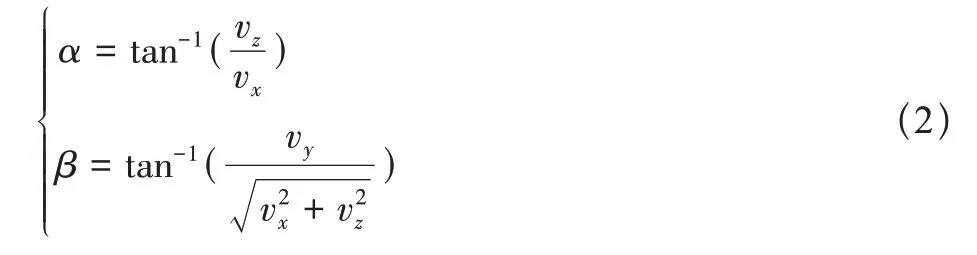
式中，[vx，vy，vz]是来流速度Va在本体坐标系{b}的投影，其值由公式可以计算获得，其中[wx，wy，wz]为风速在大地坐标系下的表示，[u，v，w]为系统速度在本体坐标系下的表示。

伞翼飞行器本体坐标系与气流坐标系之间的转换公式如下

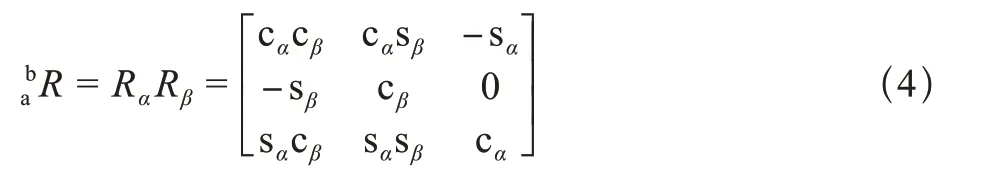
1.3 六自由度动力学方程

在伞翼飞行器完全充气展开后，除后缘下拉的状况下，伞翼可以被假设为具有一个固定的外形结构，因此，在推导伞翼飞行器六自由动力学公式时，可以假设伞翼飞行器为一个刚性整体。

根据牛顿第二定律和转动定律可以得到伞翼飞行器系统的动力学公式如下。

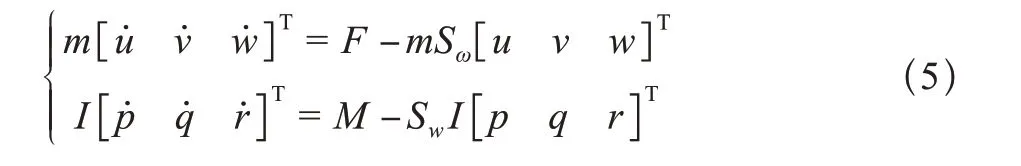
式中，m为伞翼飞行器系统质量，F、M为系统所受合力和合力矩。合力包括主要重力、气动力、推力和附加质量力，分别作用于大地坐标系、气流坐标系和本体坐标系，将其转换到本体坐标系中表示，其中，重力在本体坐标系中的表示为

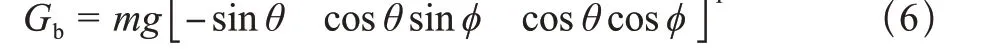
气动力在本体坐标系中的表示为

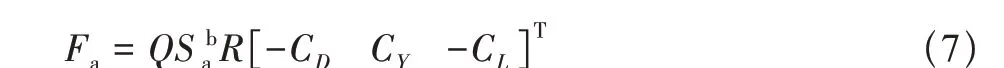
式中，Q和S分别为伞翼飞行器动压和伞翼面积；CD，CY和CL为气动力系数。

伞翼飞行器推力表示为

式中，Cδp为推力系数；δp为无量纲推力。

系统所受气动力如下

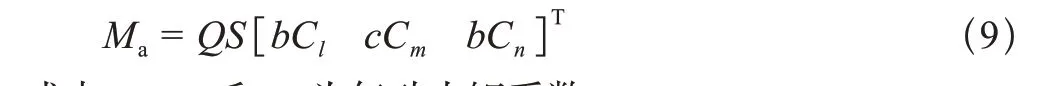
式中，Cl、Cm和Cn为气动力矩系数。

结合上述气动力和气动力矩公式，代入到动力学方程中，可得

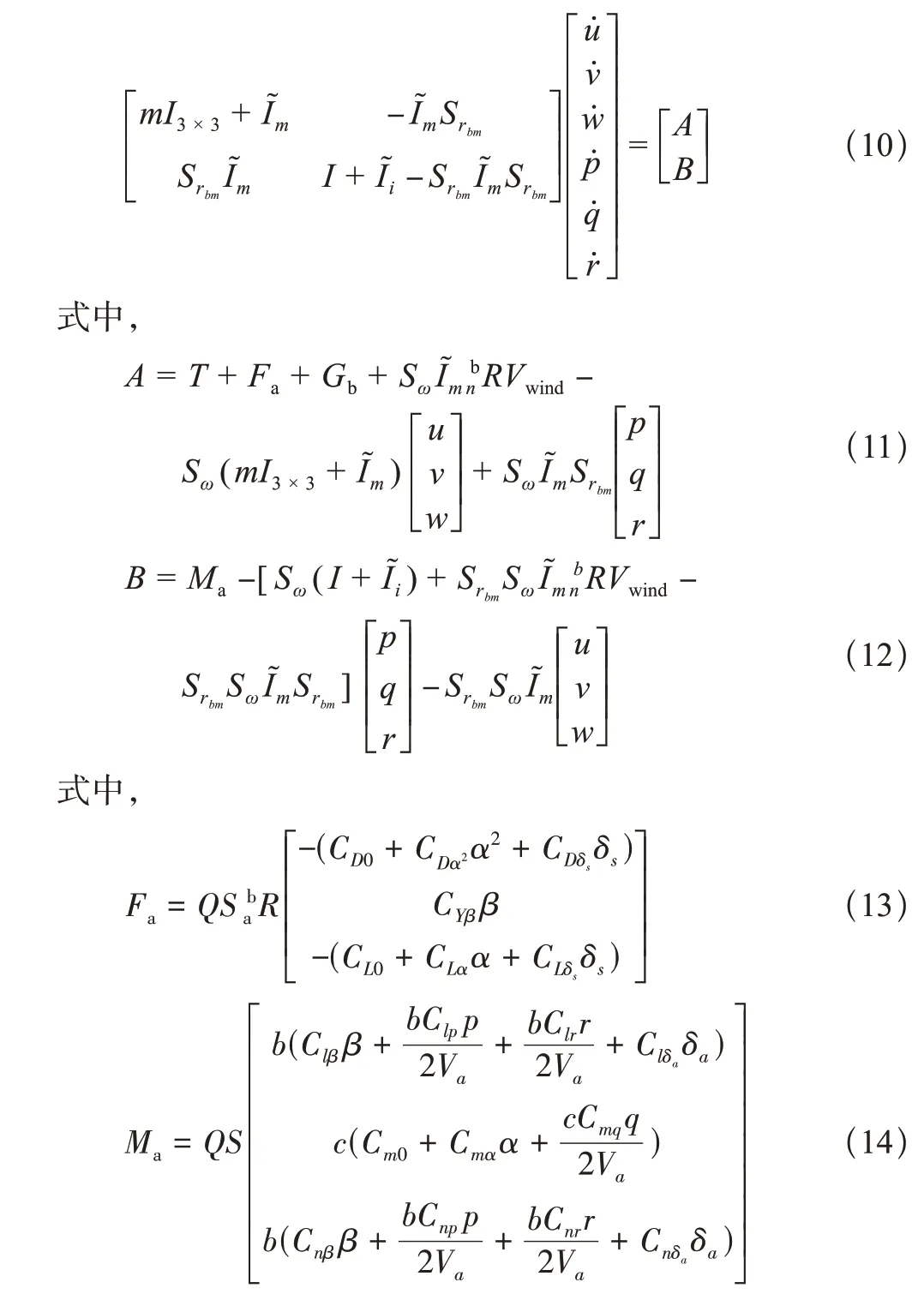
式中，I为附加质量、附加质量力矩等，为简化建模过程，在计算时，忽略不计。

2 无模型自适应控制方法

2.1 无模型自适应控制方法推导过程

飞行控制方法大体可以分为基于模型的控制方法和基于数据驱动的无模型控制方法，基于模型的控制方法适用于动力学特性明确的系统，对于复杂的非线性系统，无模型控制方法更为适用。无模型控制方法主要有PⅠD 控制、无模型自适应控制、迭代反馈整定和迭代学习控制等。

本文基于无模型自适应控制方法设计伞翼飞行器控制器，无模型自适应控制方法是侯忠生教授针对离散非线性系统于20 世纪90 年代提出的数据驱动控制算法[16]。该算法的有效性和可用性已经经过了严密的数学推导和相应的仿真验证[17]，并已经在多个领域得到验证[18-22]。

Hjalmarsson 采用迭代反馈调参方法分析非线性系统[23]，该方法也基于数据驱动，通过最小化复合控制判据来调谐参数。王卫红等总结了迭代反馈调参的发展，并指出该方法的几个特性[24]。ⅠFT-MFAC 在火箭发射过程中对三轴姿态控制的有效性也通过仿真得到了验证[25]。Wu 和Li将MFAC和ⅠFT结合，并应用于充气人造肌肉控制中[26]。

无模型自适应控制器的推导过程简单描述如下。单输入、单输出的离散非线性系统可以表示为

与控制量的迭代公式的求解算法类似，对离散非线性系统伪偏导数的评价函数可以表示成

式中，τ＞0也是权重因子，用来改变误差量和偏导函数变化对伪偏导数评价函数的影响权重。

该评价函数对Ωk求偏导极值，并置左右两端为0，整理后得到伪偏导数的迭代公式如下。

式中，Ω̂k是估计伪偏导数，是通过输入输出量解算出来的非线性系统偏导数，与真实的偏导数存在误差。

根据单输入单输出非线性系统的伪偏导数和控制量迭代公式，可以得出无模型自适应控制方法的控制方案为

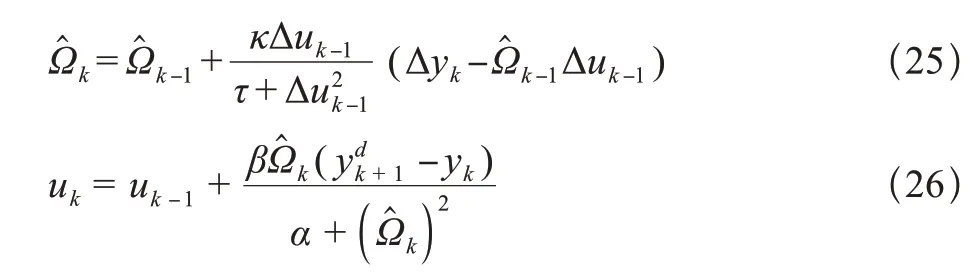
式中，为了使算法具有更强的灵活性，且保证算法收敛性和稳定性，在控制方案中增加两个步长因子β、κ∈[0，1]。

为了使该算法具有更强的适应性，估计偏导函数满足以下重置算法:当|Ω̂k|≤ε， |Δuk-1|≤ε或者sign(Ω̂k)≠sign(Ω̂1)时，Ω̂k=Ω̂1。其中，ε是一个充分小的正数。该重置算法可以使估计偏导函数具有更强的对时变参数的跟踪能力。无模型自适应控制算法的流程如图 1 所示，对于被控非线性系统，通过测量获得系统的状态，作为输入传输给无模型自适应控制器，控制器结合上一步的伪偏导数和控制量，计算本次的伪偏导数，经过伪偏导数的重置算法，获得最终的伪偏导数，并结合控制目标值计算本次的控制量输出。控制量经过限幅器，输入被控非线性系统中，控制系统做出响应，得到下一步的状态值。

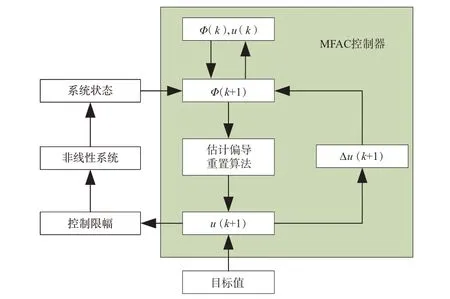
图1 无模型自适应控制算法的流程Fig.1 Process flow diagram of the MFAC method

经过上述推导，已经得到了无模型自适应控制方法，在具体应用之前，其稳定性和鲁棒性需要进一步进行分析，本文不做重点分析。

2.2 基于迭代反馈调参的无模型自适应控制方法

基于迭代反馈调参的无模型自适应控制方法是指在无模型自适应控制器的基础上，利用迭代反馈调参方法，根据实时的控制效果和控制量输出，对控制器的两个步长因子进行调谐，达到更优的输出和控制组合。

迭代反馈调参控制方法首先要构建控制系统的评价函数，然后，根据试验数据求取该评价函数的最小值，并解算出需要调谐的参数[1]。下面对反馈迭代调参方法的一般构建过程进行简要说明。

非线性系统表述如式（15）所示，系统输出如式（27）所示

式中，Γ(θ)和Ξ(θ)是简化运算符号。

将系统输出对待调谐参数θ取微分，表达式变成如下所示

相应地，控制输入函数对待调谐参数θ取微分，并利用简化符号，可以简化为式（33）和式（34）。

由式（36）、式（37）可以看出，辨识参数进行更新需要系统输出量和控制量对待辨识参数的微分，因此设置一些试验来获取这些微分量的预估值[24]。

设定参考信号和控制输入的初始值，并设计三次测试

评价函数的微分形式和海森阵可以由式（41）和式（42）得到，从而可以推导得到待辨识参数的迭代公式（38）。迭代反馈调参方法流程如图2 所示，可以总结如下:（1）设置初始参数、初始参考信号和初始控制量；（2）设置初始迭代试验，并将上述初始值代入试验中，得到初始输出；（3）计算评价函数对待辨识参数的微分值；（4）迭代计算待辨识参数；（5）根据迭代后的待辨识参数计算控制量；（6）将控制量代入非线性系统中，得到系统输出；（7）重复第三步。

2.3 基于反馈迭代调参的无模型自适应控制器设计

在无模型自适应控制算法中，有4 个参数可以进行调谐，其中两个步长因子对控制器的影响较大，因此，在本文，对于模型自适应控制器的两个步长因子进行反馈迭代调整。根据2.2节所表述的过程，基于迭代反馈调参的无模型自适应控制器设计为如下公式所示

综上，基于迭代反馈调参方法的无模型自适应控制器的参数调谐流程如图3所示。

至此，基于反馈迭代调参的无模型自适应控制器已经建立起来，由于其仅仅是对无模型自适应控制方法的参数进行调参，而且参数调整在限定范围内，因此，其稳定性和鲁棒性与无模型自适应控制方法一致。

3 基于IFT-MFAC的伞翼飞行控制仿真

利用伞翼飞行器六自由度动力学模型，设置两种跟踪轨迹、三种工作环境，分别是直线轨迹、折线轨迹和理想环境、突风环境及随机扰动环境，验证ⅠFT-MFAC控制器对伞翼飞行器的轨迹跟踪控制效果。将PⅠD 控制器、ADRC 控制器和MFAC控制器设置为对照组。

3.1 理想环境

3.1.1 直线轨迹

在基于迭代反馈调参的伞翼飞行器无模型自适应控制器的仿真中，直线轨迹的设置与MFAC 控制器的验证过程一致，控制效果如图4所示，由图4中可以看出，4种控制器均能较好地控制伞翼飞行器跟踪该直线轨迹。跟踪过程中的距离误差和控制输入量如图5所示，在4种控制器的作用下，距离误差最终归为0，峰值误差小于10m，其中，ADRC控制器、MFAC 控制器和ⅠFT-MFAC 控制器的距离误差平均值相近，略大于PⅠD控制器。MFAC控制器和ⅠFT-MFAC控制器的控制效果相近。

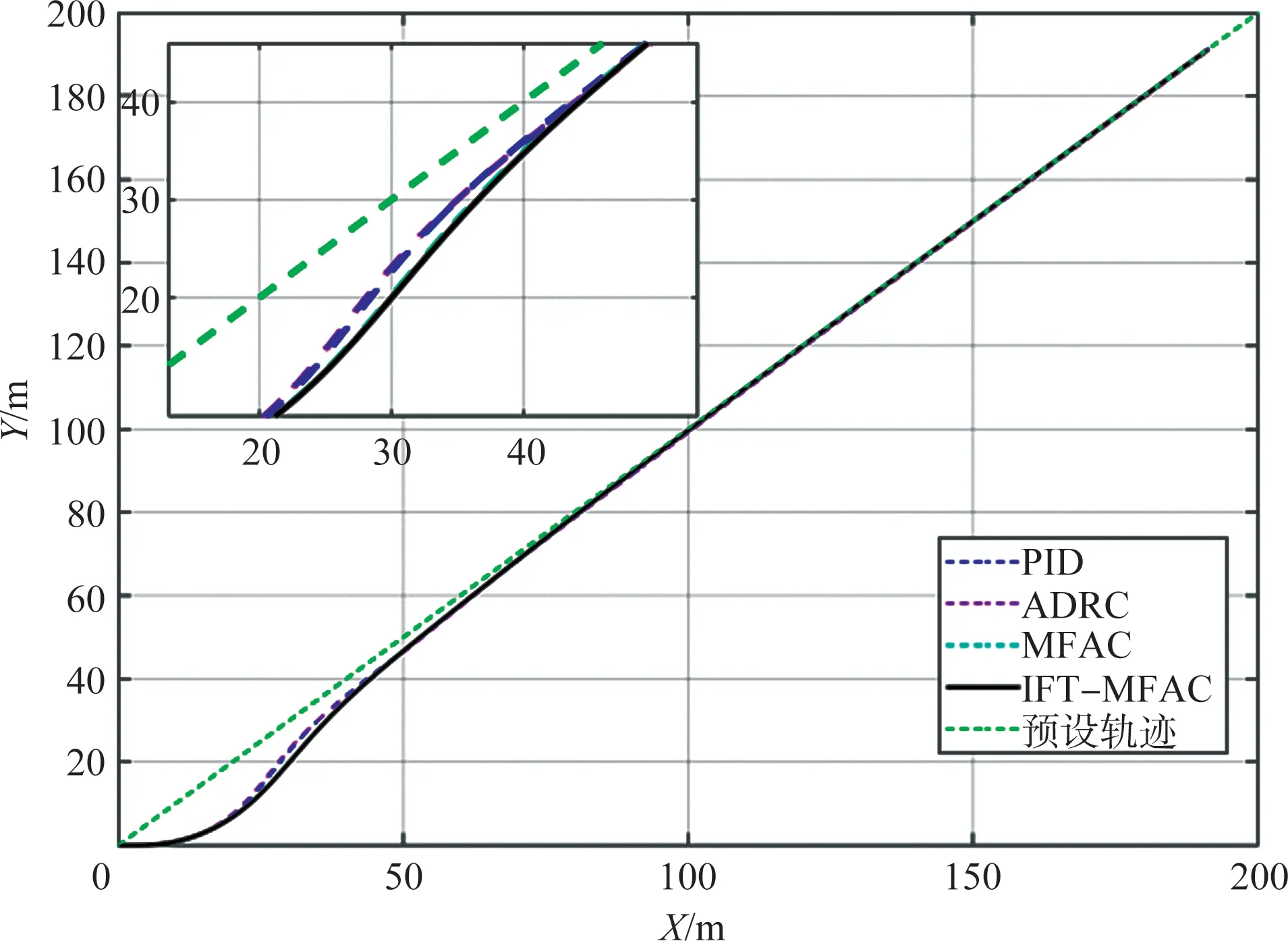
图4 理想环境下直线轨迹跟踪效果Fig.4 Straight-line trajectory under ideal conditions

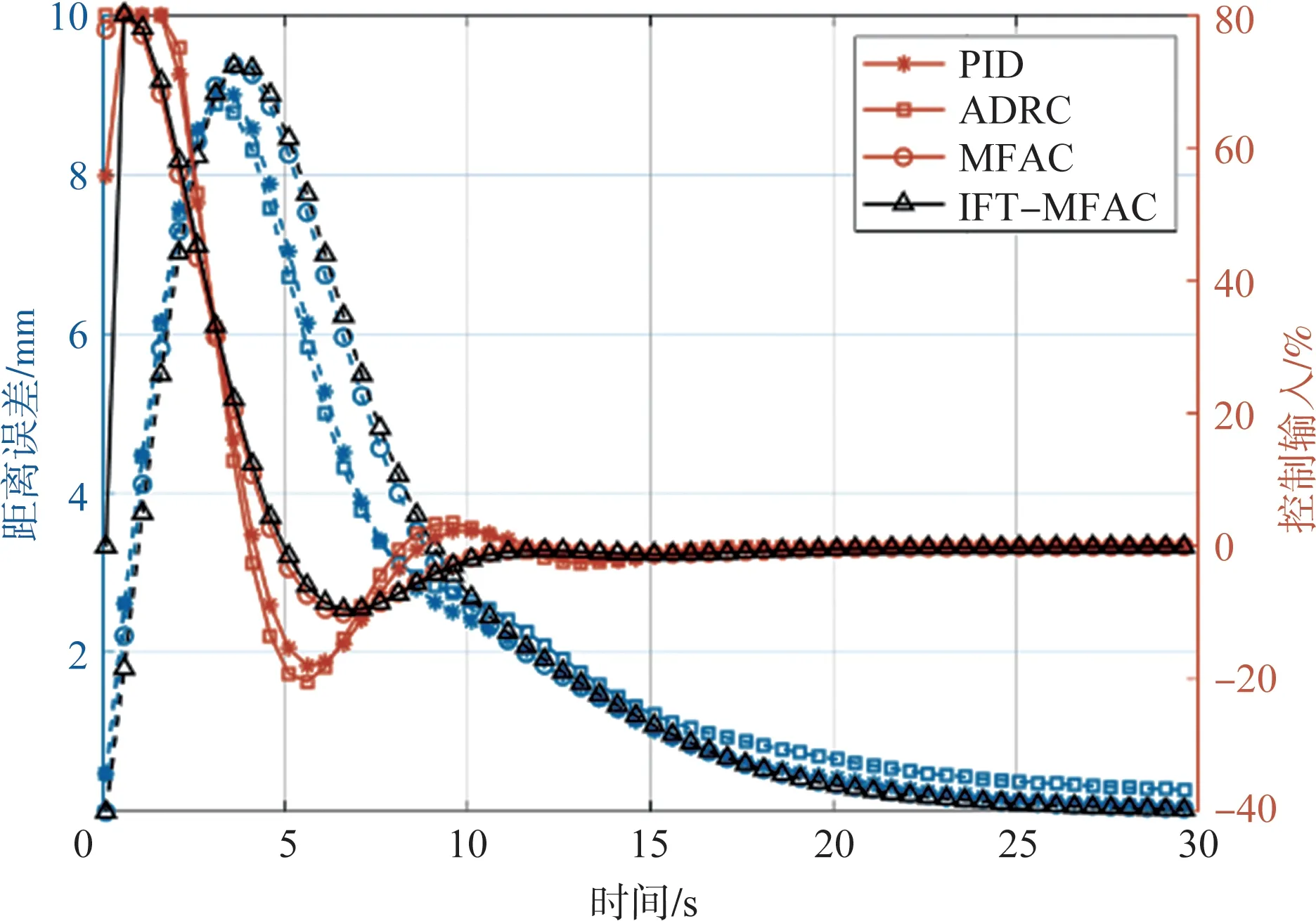
图5 理想环境下直线轨迹跟踪距离误差和控制量Fig.5 Distance error and control value of the straight-line trajectory under ideal conditions

4种控制器的控制量在大约15s后均变为0。MFAC控制器和ⅠFT-MFAC控制器的平均控制量小于PⅠD控制器和ADRC控制器，且超调量远小于另两种控制器，其控制量均方差为0.19、0.194、0.175和0.174（分别对应于PⅠD控制器、ADRC控制器、MFAC控制器和ⅠFT-MFAC控制器，如无特殊说明，顺序下同）。因此，MFAC 控制器和ⅠFT-MFAC 控制器具有更小的控制量均方差和更平稳的控制效果。ⅠFTMFAC控制器两个待调谐参数的变化随着跟踪距离误差减小，控制量步长因子也随之下降，伪偏导数的步长因子在控制量变化剧烈阶段存在扰动，随后保持在初始值附近，说明该初始值的选取比较靠近最优值。

3.1.2 折线轨迹

为了验证伞翼飞行器在ⅠFT-MFAC控制器控制下的转弯特性，本节设计了方形折线轨迹，伞翼飞行器在4种控制器作用下对该轨迹的跟踪效果如图6 所示。由图6 中可以看出，伞翼飞行器在4种控制器的作用下，均能较好地跟踪该轨迹，图中放大部分为第二个转弯点伞翼飞行器的轨迹跟踪情况，可以看出，在该种情况下，PⅠD 控制器和ADRC控制器的轨迹跟踪效果好于MFAC控制器和ⅠFT-MFAC控制器，具体跟踪过程中的距离误差如图7 所示。将转弯点的目标阈值设置为5m，以判断伞翼飞行器是否到达预设目标点。由图7 中可以看出，伞翼飞行器在每个转折点都会出现距离误差瞬间增大的情况，这是因为当判断伞翼飞行器到达目标点后，其目标点切换到下一个，相应的距离误差计算切换到下一条航线。伞翼飞行器在4种控制器作用下的距离误差平均值分别为3.31m、3.64m、3.33m 和3.38m，ⅠFT-MFAC控制器的收敛速度更快，超调量更小。

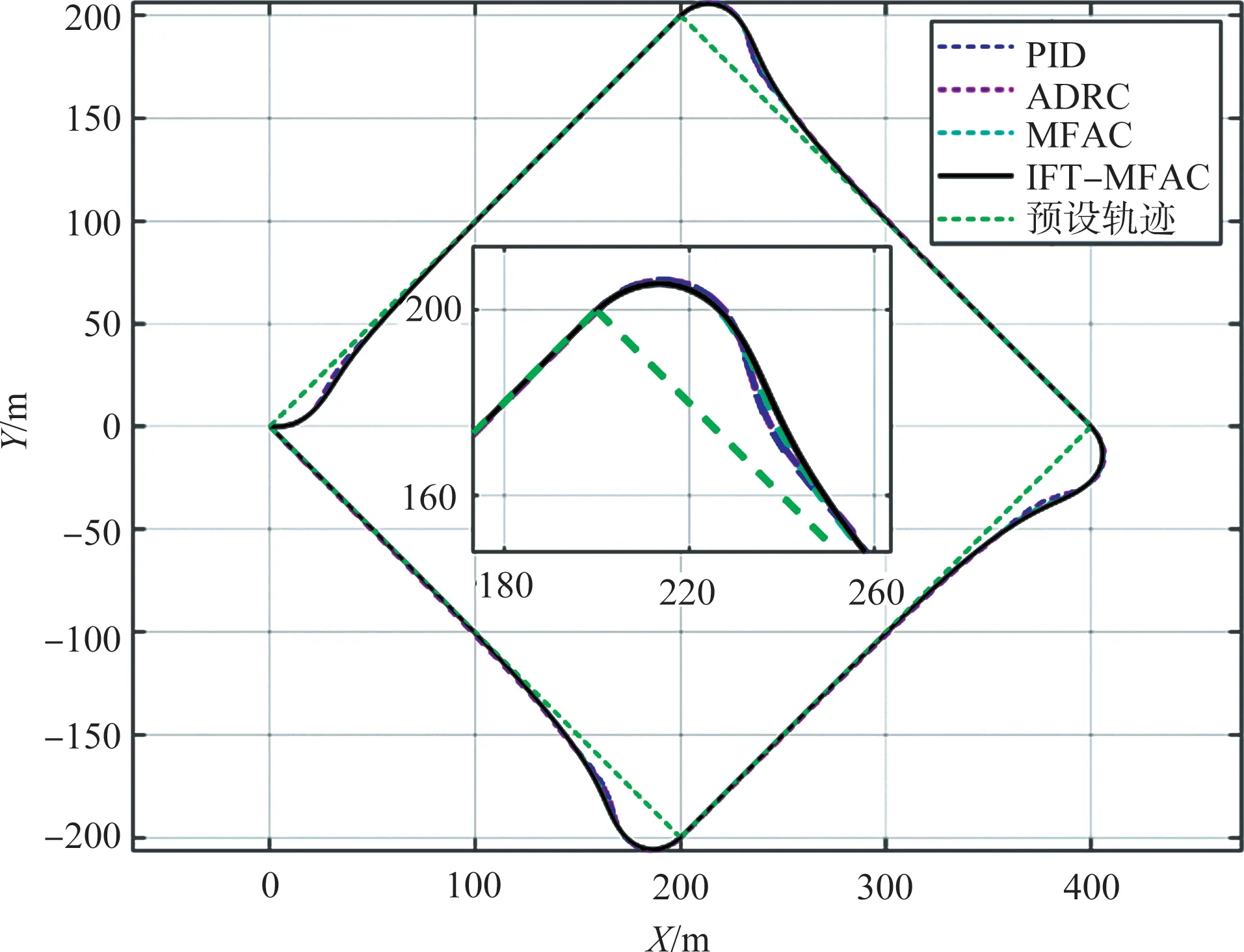
图6 理想环境下折线轨迹跟踪过程Fig.6 Polyline trajectories under ideal conditions

图7 理想环境下折线轨迹跟踪距离误差Fig.7 Distance error of the polyline trajectories under ideal conditions

基于4 种控制器的伞翼飞行器飞行控制系统在折线轨迹的控制量输出如图8所示。由图8中可以明显看出，在转弯点时，MFAC控制器和ⅠFT-MFAC控制器的控制超调量远小于另两种控制器，且ⅠFT-MFAC 控制器更小一些。另外，4 种控制器输出控制量的均值分别为11.1%、11.3%、9.6%和9.5%，相应的均方差为0.237、0.239、0.223和0.218，由此可见，ⅠFT-MFAC控制器具有更小的控制量和更平稳的控制效果。

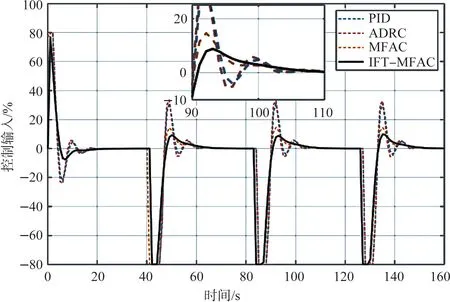
图8 理想环境下折线轨迹跟踪过程控制量Fig.8 Control input values of the polyline trajectory under ideal conditions

3.2 随机扰动环境

在伞翼飞行器的实际飞行过程中，系统的测量数据会存在扰动，在本节中，针对随机扰动存在的情况进行仿真，验证伞翼飞行器在4种控制器的作用下对两种轨迹的跟踪效果，扰动值的设置与MFAC控制器的扰动环境设置一致。

3.2.1 直线轨迹

在随机扰动环境中，4种控制器控制伞翼飞行器对直线轨迹的跟踪情况如图9 所示。与理想环境和突风环境相比，随机扰动情况下的跟踪效果不够平滑。图9 中就部分细节进行放大，以便于进一步观测其跟踪情况，4种控制器整体的跟踪效果与另两种情况类似。轨迹跟踪误差和控制量输出分别如图 10和图11所示。由图中可以看出，轨迹跟踪误差平均值和控制量平均值均近似，轨迹跟踪误差的平均值分别为2.17m、2.23m、2.40m和2.19m，控制量的均值分别为22.1%、30.8%、22.4%和22.3%，控制量均方差分别为0.19、0.228、0.182 和0.181。MFAC 控制器和ⅠFT-MFAC 控制器的控制量均方差最小。

图9 随机扰动环境下直线轨迹跟踪过程Fig.9 Straight line trajectory under random disturbance conditions

图10 随机扰动环境下直线轨迹跟踪距离误差Fig.10 Distance error of the straight-line trajectory under random disturbance conditions

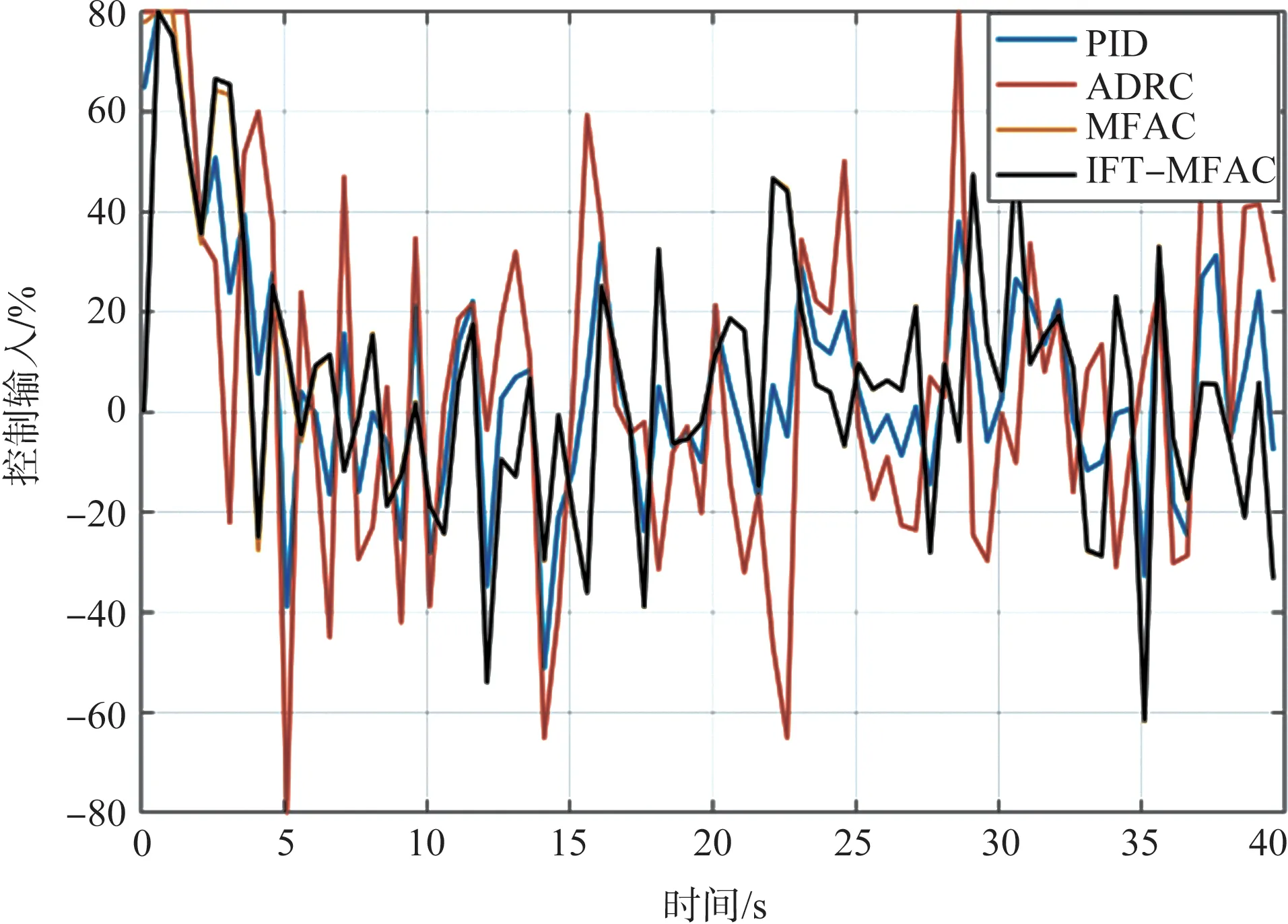
图11 随机扰动环境下直线轨迹跟踪过程控制量变化Fig.11 Control input value of the straight-line trajectory under random disturbance conditions

3.2.2 折线轨迹

在随机扰动情况下，4种控制器控制伞翼飞行器对折线轨迹的跟踪情况如图12所示，所有控制器均能取得较好的控制效果，第一个转折点被放大，以便于观看轨迹跟踪细节。MFAC控制器和ⅠFT-MFAC控制器的超调量要小于另两种控制器。4 种控制器的轨迹跟踪误差如图13 所示，其平均值分别为4.23m、4.48m、3.84m和3.81m，MFAC控制器和ⅠFT-MFAC 控制器的距离误差平均值小于另两种控制器。从放大部分可以看出，MFAC 控制器和ⅠFT-MFAC 控制器到达第二个转折点的时间较另两种控制器提早约2s，这意味着伞翼飞行器在这两种控制器控制下实际飞行路径小于另两种控制器，这与轨迹跟踪过程的超调量一致，即具有较小的超调量，更小的时间消耗。

图12 随机扰动环境下折线轨迹跟踪过程Fig.12 Polyline trajectory under random disturbance conditions

图13 随机扰动环境下折线轨迹跟踪距离误差Fig.13 Distance error of the polyline trajectory under random disturbance conditions

4 种控制器的控制量输出值如图14 所示，其平均值分别为26.5%、34.5%、25.5%和25.3%，相应的均方差为0.234、0.254、0.224 和0.223。在此仿真试验中，MFAC 控制器和ⅠFT-MFAC 控制器比另两种控制器取得了更小的控制量平均值和控制量均方差，控制效果相对更加平滑。

图14 随机扰动环境下折线轨迹跟踪过程中控制量变化Fig. 14 Control input value of the polyline trajectory under random disturbance conditions

4 结论

通过设计基于迭代反馈调参的伞翼飞行器无模型自适应控制系统，并经过理想环境和随机扰动环境对该控制器的控制效果进行仿真验证，可以看出，该控制器可以控制伞翼飞行器对直线轨迹和折线轨迹进行有效的跟踪。与PⅠD控制器、ADRC 控制器和无模型自适应控制器的控制效果相比，ⅠFT-MFAC控制器在复杂环境下的控制效果更好，尤其是在随机扰动环境下对折线轨迹的跟踪效果。其轨迹跟踪误差更小，控制量的平均值和均方差更小。在仿真过程中，可以看到，无模型自适应控制器的两个步长因子随着误差量和控制量的变化而发生变化，数值在稳定过程中逐渐减小，但是由于扰动环境的存在，控制量的步长因子一直保持在边界值附近。因此，基于反馈迭代调参的伞翼飞行器无模型自适应控制器可以满足对伞翼飞行器在复杂工况下的轨迹跟踪任务需求。