基于核心素养的解题反思——以一道解析几何题为例

骆晓梅 付中华

广东省珠海市斗门第一中学 广东省中山市华侨中学

在高三复习中，教师应如何引导学生解题反思总结，充分发挥题目的价值，提高教学效率，提升学生的解题能力，发展学生的核心素养？本文中以一道解析几何题为例，进行了探讨.

1 试题及解答

原题已知动圆E经过定点D(1,0)，且与直线x=-1相切，设动圆圆心E的轨迹为曲线C.

(1)求曲线C的方程；

(2)设过点P(1,2)的直线l1,l2分别与曲线C交于A,B两点，直线l1,l2的斜率存在，且倾斜角互补，证明：直线AB的斜率为定值.

解析：(1)y2=4x(解答过程略).

图1

(2)证法一：如图1，由题可知直线l1,l2的斜率互为相反数，且不为0.设直线l1的方程为y=k(x-1)+2(k≠0)，A(x1,y1),B(x2,y2).

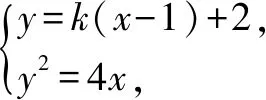
k2x2-(2k2-4k+4)x+(k-2)2=0.

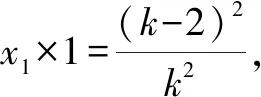
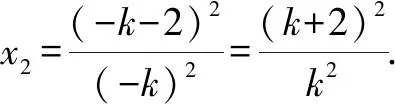
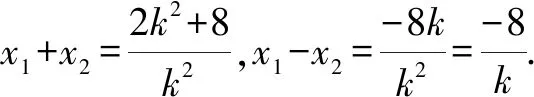
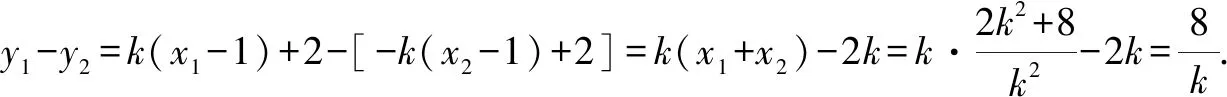
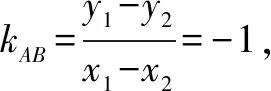
证法二：易知直线AB的斜率存在且不为0.设直线AB的方程为y=kx+b，A(x1,y1),B(x2,y2).

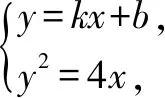
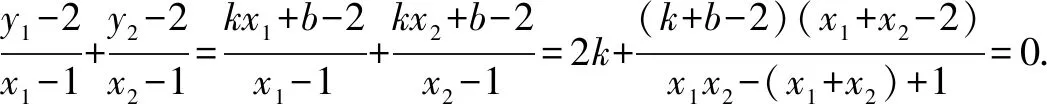
将x1+x2与x1x2表达式代入上式解得k=-1，故直线AB的斜率为定值-1.

以上两种证法是学生在解题中出现的最常见的方法，也是通性通法.看似平常的题目和解法，但其背后却有许多地方值得我们好好反思研究.

2 对解法的反思

2.1 对几何条件代数化的反思

本题中是将倾斜角互补转化为了斜率和为0.将题目中的几何关系，准确地转化为代数关系，常常是解题的关键.而恰当的转化，常常能优化解题过程.比如两直线垂直，可以转化为斜率之积为-1，也可以转化为向量数量积为0，前者需要保证两直线的斜率都存在，否则需要分类讨论，后者优势明显.有时候，可能需要进行比较复杂的转化.

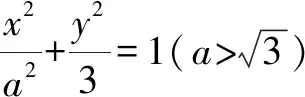
(1)求椭圆的方程；

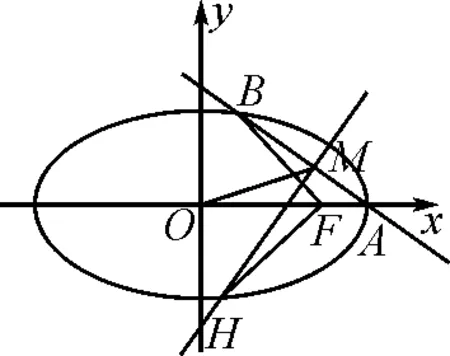
图2

(2)如图2，设过点A的直线l与椭圆交于点B(B不在x轴上)，垂直于l的直线与l交于点M，与y轴交于点H，若BF⊥HF，且∠MOA≤∠MAO，求直线l斜率的取值范围.

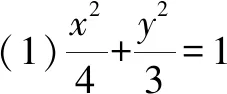
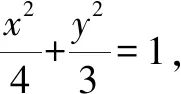
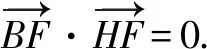
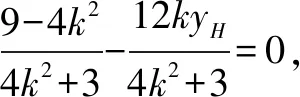
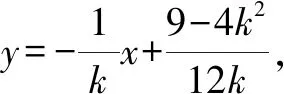
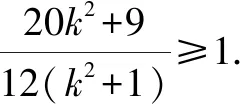
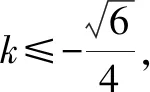
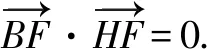
2.2 对设直线方程形式的反思

一般情况下，学生最常设的直线方程形式为点斜式或斜截式，但也常常忽略了对直线的斜率进行判断或讨论.很多时候，如果可以判断或已经知道直线经过x轴上的点(t,0)，特别是斜率可以不存在但是不为0时，则可设直线方程为x=my+t，既可以避免分类讨论，又可以简化后期的书写量与运算量，提高运算速度和准确度.原题若采用x=my+t，则证题过程要简洁很多.

原题第(2)问的第三种证法如下.

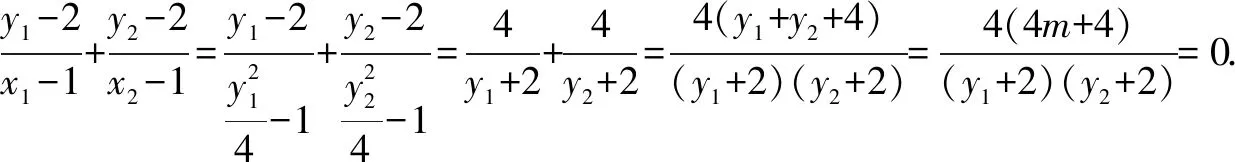
所以m=-1，即直线AB的斜率为定值-1.

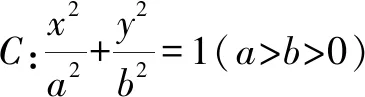
(1)求椭圆C的方程；

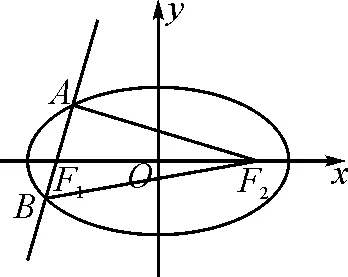
图3

(2)如图3，设过点F1的直线l与C交于A,B两点，求△ABF2面积的最大值.

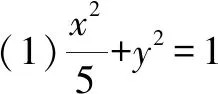
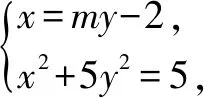
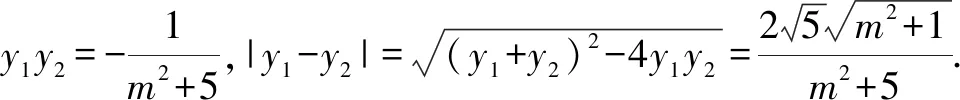
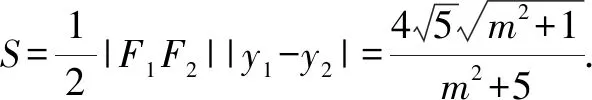
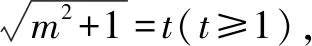
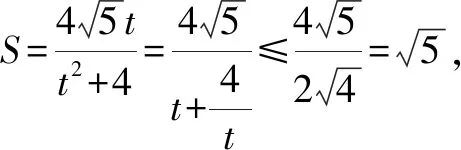
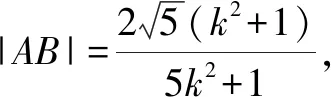
2.3 对消元方法的反思

原题第(2)问的证法一、二中，利用了点在直线上消去了y1,y2.证法三中，可以利用点在直线上消去x1,x2，但考虑到抛物线方程的特殊性，利用点在曲线上消去了x1,x2，则显得更方便快捷.在实际解题时，需要灵活地考虑.另一方面，三种解法中均是消去了x1,x2,y1,y2得到关于参数k(或m)的表达式，如果直接消去x1,x2,y1,y2不方便时，则也可以考虑消去参数k(或m).

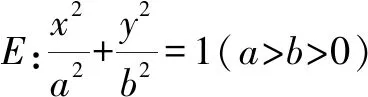
(1)求椭圆E的标准方程；

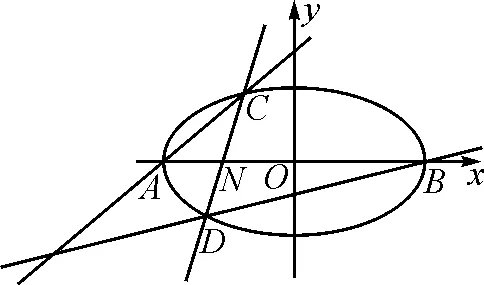
图4

(2)如图4，设椭圆E的左、右顶点分别是A,B，过定点N(-1,0)的直线与椭圆E交于C,D两点(与点A,B不重合)，证明：直线AC,BD的交点的横坐标为定值.

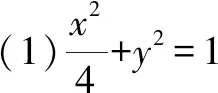
(2)易知CD的斜率不为0.设CD:x=my-1，C(x1,y1),D(x2,y2).

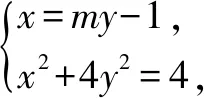
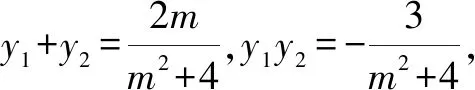
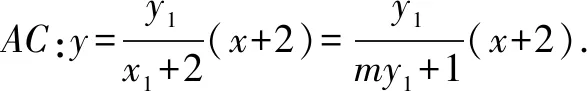
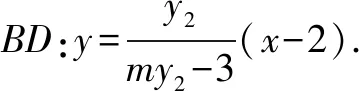
即直线AC,BD的交点的横坐标为定值-4.

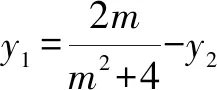
3 对新的解题方法的探索反思

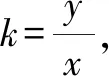
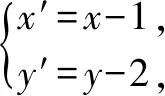
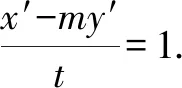
(t-4m)y′2+4(m+1)x′y′-4x′2=0.

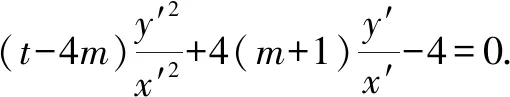
故直线AB方程为x′=-y′+t，于是x-1=-y+2+t,即y=-x+t+3，所以直线AB的斜率为定值-1.

从解答过程来看，如果设直线AB方程为mx′+ny′=1，利用“1 ”的代换将方程齐次化则更加自然.同时发现，如果两直线斜率之和或积为定值，本方法都适用.

4 对原题目的反思拓展

原题目中斜率之和为常数0时，直线AB的斜率是一个定值.如果斜率之和是一个非零的常数p，直线AB有特定的性质吗？如果斜率之积为一个非零的常数q，直线AB有特定的性质吗？

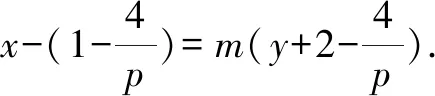
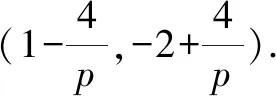
如果将抛物线改为椭圆、双曲线，或者改变点P的坐标，依然有类似的结论.具体则由学生自行探究.

在复习时，学生不应是为了做题而做题，教师不是为了讲题而讲题.作为教师，需要深挖题目背后的价值，让一道题充分发挥其应有的价值.指导学生学会反思、学会总结，引导学生举一反三，促进学生的深度学习，提升思维能力，落实核心素养.Z