山区高速公路隧道仰拱拆换结构变形机制
杨沛文, 刘鎏, 周小涵*, 刘新荣, 林彬彬
(1.重庆大学土木工程学院, 重庆 400045; 2.中交路桥建设有限公司, 重庆 400045)
随着交通基础设施迅速发展,中国隧道工程建设的速度和数量也在不断增加。截至2020年底,中国隧道总数已达16 789座,总计达到19 630 km[1]。中国已经成为世界上建设和运营公路隧道最多的国家。隧道是修建在地下岩土介质中的半隐蔽工程,随着运营时间的增加,诸如裂缝、渗漏水等衬砌病害也会逐渐显露[2]。这些病害会对隧道结构的耐久性和承载性能产生影响,缩短隧道的服役时间,更严重地会威胁结构稳定,影响行车安全[3]。
仰拱是隧道的围岩衬砌体系中的必不可少的组成部分[4];受施工或水文地质环境等因素影响,仰拱时常会产生底板开裂和变形、侧沟开裂和变形、底板沉陷、面层翻浆和隆起等问题[5]。近年来,有关仰拱病害的案例不在少数,王延方等[6]调查了某泥岩隧道,发现路面裂缝延伸范围达300 m,最长裂缝达50 m,最大错台约10 cm,严重危及行车安全;安江市某隧道路面开裂,路面呈现中间高两边低,电缆沟也出现和二衬表面也出现了开裂情况,裂缝长度达到100 m,平均缝宽7~8 mm,最大缝宽2 cm;雪峰山隧道开挖后,隧道进口段衬砌尤其是仰拱填充部分出现大量裂缝,裂缝上宽下窄,呈“V”字形,左线仰拱填充结构裂缝最深约82 cm,有限仰拱填充结构裂缝最深约为129 cm[7]。这些案例都表明,仰拱病害严重影响隧道结构的稳定性和行车安全。
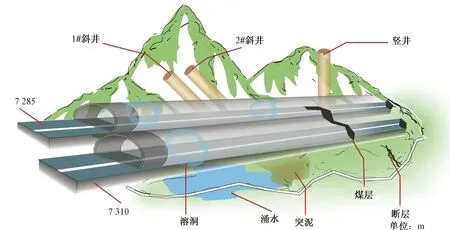
图1 隧道与山体位置关系图Fig.1 Tunnel and mountain location relationship map
目前,针对仰拱病害问题的处置方法主要有:①做好地下水引排;②在拱脚处采用注浆钢花管设置锁脚,对拱脚部分围岩进行加固;③对基底进行注浆加固以改善围岩力学性能;④当仰拱结构难以满足实际受力要求,则需进行拆换处理。部分学者也对隧道仰拱病害治理做了相关研究,邓少军等[8]针对高速公路边墙开裂问题提出采用注浆钢花管锁脚、衬砌结构加固等方法进行处理;张素磊等[9]对置换后的衬砌结构受力特征进行了现场测试,并结合测试结果对衬砌置换的适用性进行了讨论;张羽军等[10]针对隧道施工中大变形病害的成因展开研究,分析认为变形段病害产生是由于地应力作用、围岩性质和地下水综合导致;崔连友等[7]用“荷载-结构”法和现场实验发现作用在仰拱中心水压较大是使得仰拱填充结构开裂的主要原因;汪旵生[11]通过数值模拟、现场测试和观察论证了微型桩加固能有效减小仰拱隆起,防止仰拱填充结构的“V”字形裂缝的发展;李林毅等[12]基于FLAC3D软件提出一种用于反演由水压力导致的隆起病害的方法,并提出采用“施作降压孔+隧底注浆锚固+增设泄水孔+地表处理”的综合整治措施。对于病害特别严重的隧道,有时会采用换拱的方法,例如新建的兰新铁路第二双线大梁隧道[13]。现有研究中关于衬砌拆换的报道主要集中于建设期隧道。与建设期隧道不同,运营期隧道的围岩通常趋于稳定,使得其受力和变形都与建设期隧道存在较大差异,而目前关于运营期隧道衬砌拆换工程的报道尚少,且对衬砌拆换以及拆换过程中的结构变形机制研究还未见报道。
针对结构拆除的影响分析最为常见研究方法是数值模拟,如周建军等[14]在研究拱圈支架拆除顺序时,运用数值模拟分析不同拆除方案的优劣;高文乐等[15]利用有限元软件对框架结构爆破拆除倒塌这一过程进行了数值模拟。因此现以西南某山区高速公路隧道仰拱拆换工程为案例,通过建立有限元模型分析不同拆换方案对隧道结构稳定性的影响,以期为今后运营隧道仰拱拆换处理提供工程借鉴和参考。
1 工程概况
依托隧道位于中国西南山区,区域构造具有背斜陡急、向斜宽缓的“隔挡式构造”特征。隧道围岩主要为Ⅲ、Ⅳ为主,局部为Ⅴ级。隧道的走向与山体的位置关系如图1所示。隧区地下水中富含大量硫酸根离子和氯离子。该隧道在运营过程中出现了衬砌、路面开裂、电缆沟及二衬混凝土严重腐蚀等病害,且病害有不断加剧的趋势。为避免隧道病害的继续发展对结构安全性造成影响,对部分路面严重受损段落进行仰拱的拆换。仰拱及路面变形的处治方案为拆除原C25混凝土仰拱,重新施作C45防腐混凝土。
选择隧道右线某腐蚀严重需进行仰拱拆换的典型段落进行仰拱拆换研究,该段围岩为V级围岩,隧道断面如图2所示,初期支护为C20喷射混凝土,厚度为25 cm,φ8钢筋网20 cm×20 cm, I18型钢拱架纵向间距50 cm,锚杆为R25中空注浆锚杆长350 cm,间距100 cm×50 cm(纵向),复合防水层,二次衬砌为C25砼衬砌厚45 cm,仰拱为C25厚45 cm。

图2 隧道断面支护结构图Fig.2 Structural drawing of tunnel section support
2 数值模型
2.1 模型建立
数值模拟采用Midas GTS NX软件,建立了地层与隧道结构的三维有限元模型。根据经验,隧道的影响范围为3~5倍洞径[16],隧道跨度约为11 m,高度约为9 m,隧道的等效直径D约为10 m。故取模型左右边界距隧道边墙50 m(5D),下边界距隧道拱底55 m(5.5D);该模型验证段埋深为300 m,为简化模型,取上边界距隧道拱顶100 m(10D),并在上边界加上200 m土层的压力;隧道沿纵向取120 m,其中0~30 m和90~120 m为未拆换段,30~90 m共60 m为拆换段。将拆换段开始位置记为Y=0,拆换段末端记为Y=60。
模型尺寸为120 m(纵向)×110 m(左右边界距离)×165 m(上下边界距离),模型下边界为全约束,左右边界约束X轴方向位移,前后边界约束Y轴方向位移,上边界为自由面。在实际建模过程中,隧道的喷射混凝土、二衬、仰拱均采用实体单元模拟,锚杆采用1D植入式桁架模拟,均按弹性材料考虑。围岩采用实体单元模拟,服从摩尔-库伦屈服准则。隧道的网格划分及拆换段示意图如图3所示。
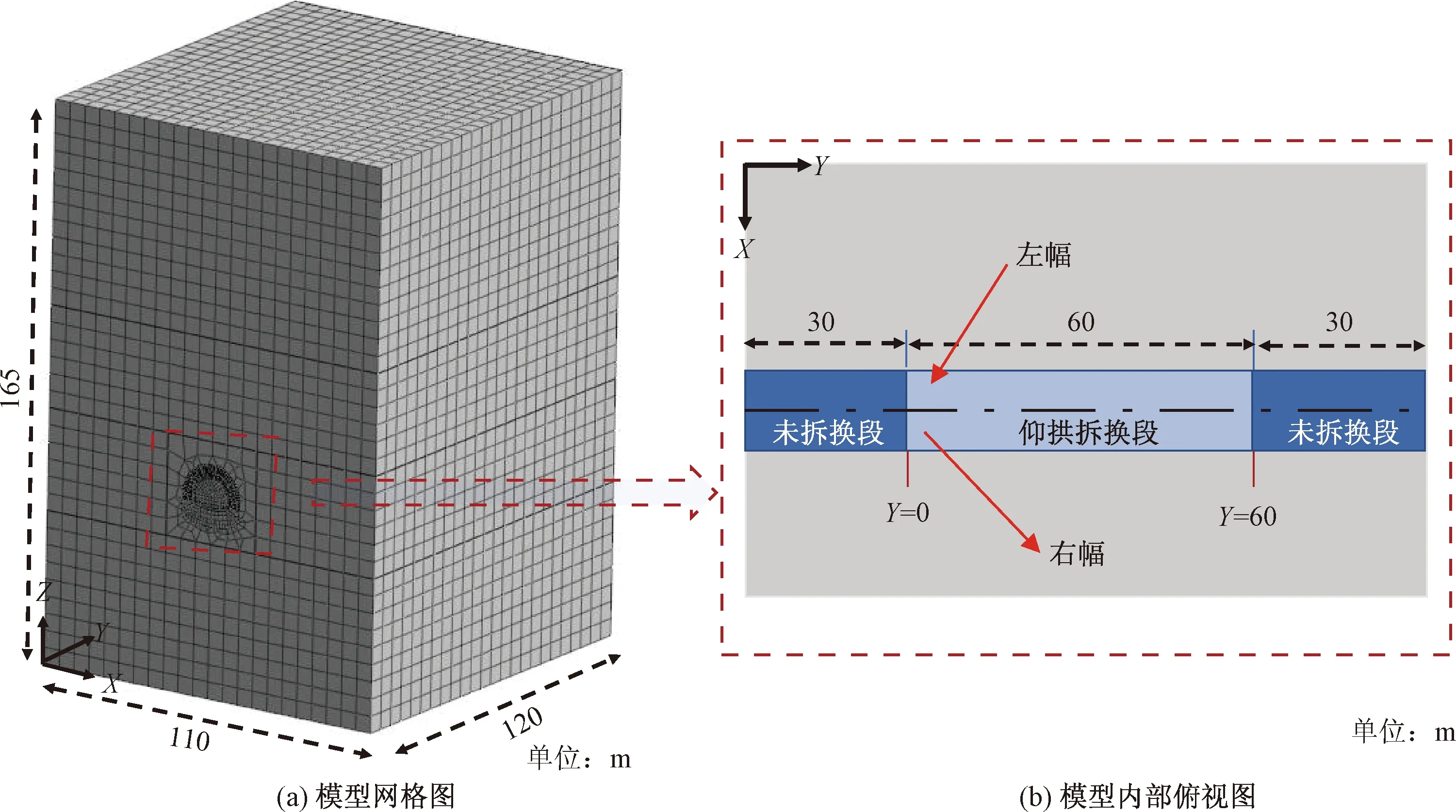
图3 模型网格划分及隧道内部示意图Fig.3 Mesh generation of model and schematic diagram of tunnel interior
2.2 材料参数
围岩参数根据隧道的地勘资料选取,对于衬砌结构参数,由于钢拱架与喷射混凝土实际上是紧密连接的,两者共同变形、受力,因此建模中的初期支护参数是将钢拱架的弹性模量折算给喷射混凝土的[17],钢筋混凝土二次衬砌也同样考虑,计算公式为
(1)

表1 材料计算参数Table 1 Numerical simulation parameters
2.3 模型验证
现场仰拱采用跳槽拆换,单次拆换距离为6 m,60 m拆换段共分为10段。具体拆换工序为:首先按顺序拆换奇数段的仰拱,在奇数段仰拱拆换完成后对偶数段进行拆换,其中每段仰拱均为先拆换左幅再拆换右幅。仰拱拆换示意图如图4所示。
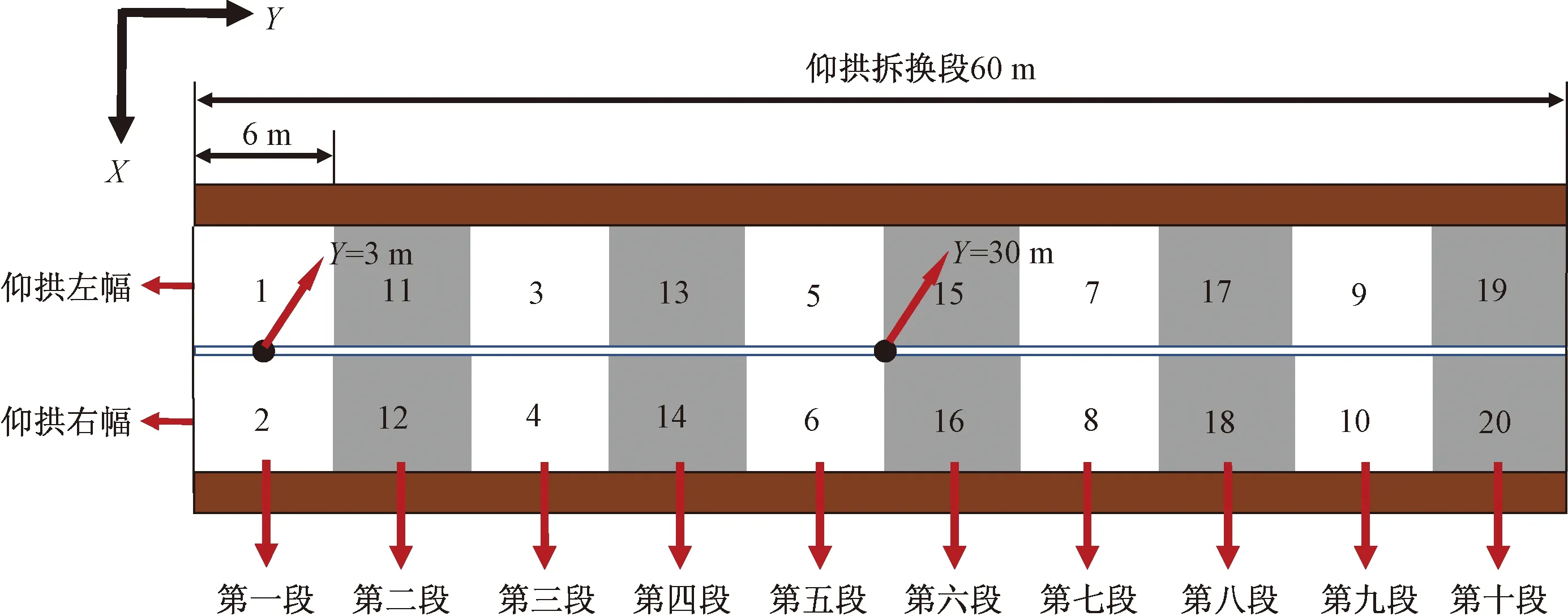
数字序号1~20表示拆换先后顺序图4 仰拱跳槽拆换示意图Fig.4 Schematic diagram of removal and replacement of inverted arch
现场监测段共设有5个测点,测点在仰拱拆换过程中对拱顶沉降进行监测。在拆换完成时拱顶的沉降约为2.0 mm,监测数据与计算数据的对比如图5所示。由于测点之间的距离较近,因此计算数据与监测数据中各点拱顶沉降量之间的差距较小,模拟得到的拱顶沉降曲线接近直线。

图5 监测数据与模拟数据比较Fig.5 Comparison of monitoring data and simulation data
监测数据与计算数据之间的差距小于20%,可认为建立的数值模型与实际比较贴近。
3 仰拱拆换过程中隧道整体变形规律分析
3.1 横截面变形规律
以拆换段中间截面(Y=30 m处)为例,比较拆换前后隧道横截面的变形情况。为了便于观察,将隧道变形部分做了适当的放大,如图6所示。
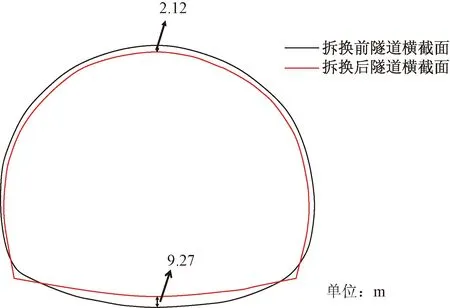
图6 拆换前后隧道横截面变化Fig.6 Change of tunnel cross section before and after replacement
在仰拱拆除过程中,由于拱脚处于悬空状态,在上部荷载和两侧围岩的挤压下,隧道拱脚在竖直方向产生了约4.50 mm的沉降且在水平方向产生了0.87 mm的收敛变形。除了拱脚之外,隧道的变形主要发生在拱顶和拱底位置处,在图6的截面中,拱底隆起了约9.27 mm,拱顶下降了约2.12 mm。
总体来说,在仰拱拆换中,由于外部荷载的作用,隧道横截面呈现出向内收缩的变形趋势。隧道拱脚和拱底处容易产生较大的变形,拱顶也会产生少量变形。因此,在施工中要特别注意对衬砌悬空的位置做好临时支撑。
在隧道容易发生变形的3个位置中,选取隧道的拱顶和拱底为研究对象,分析隧道在拆换过程中结构变形机制。
3.2 时间变形规律
在仰拱拆换过程中,原本由拆换部分仰拱承担的围岩荷载将转移到相邻的仰拱上,对相邻的仰拱产生附加影响,主要探讨了拆换过程中,隧道拱顶和拱底的时间变形规律。
由于拆换段两端和中间部分的拱顶沉降和拱底隆起变形规律不同,因此分别选取模型中距离拆换段起始位置3 m和30 m处的点(Y=3 m和Y=30 m)来研究隧道结构不同位置随时间的变化规律,两点位置如图4所示。分别绘制两点的拱底和拱顶的时间变形曲线,如图7和图8所示。

图7 两点拱底随时间变形变化曲线Fig.7 Time history deformation curve of arch bottom
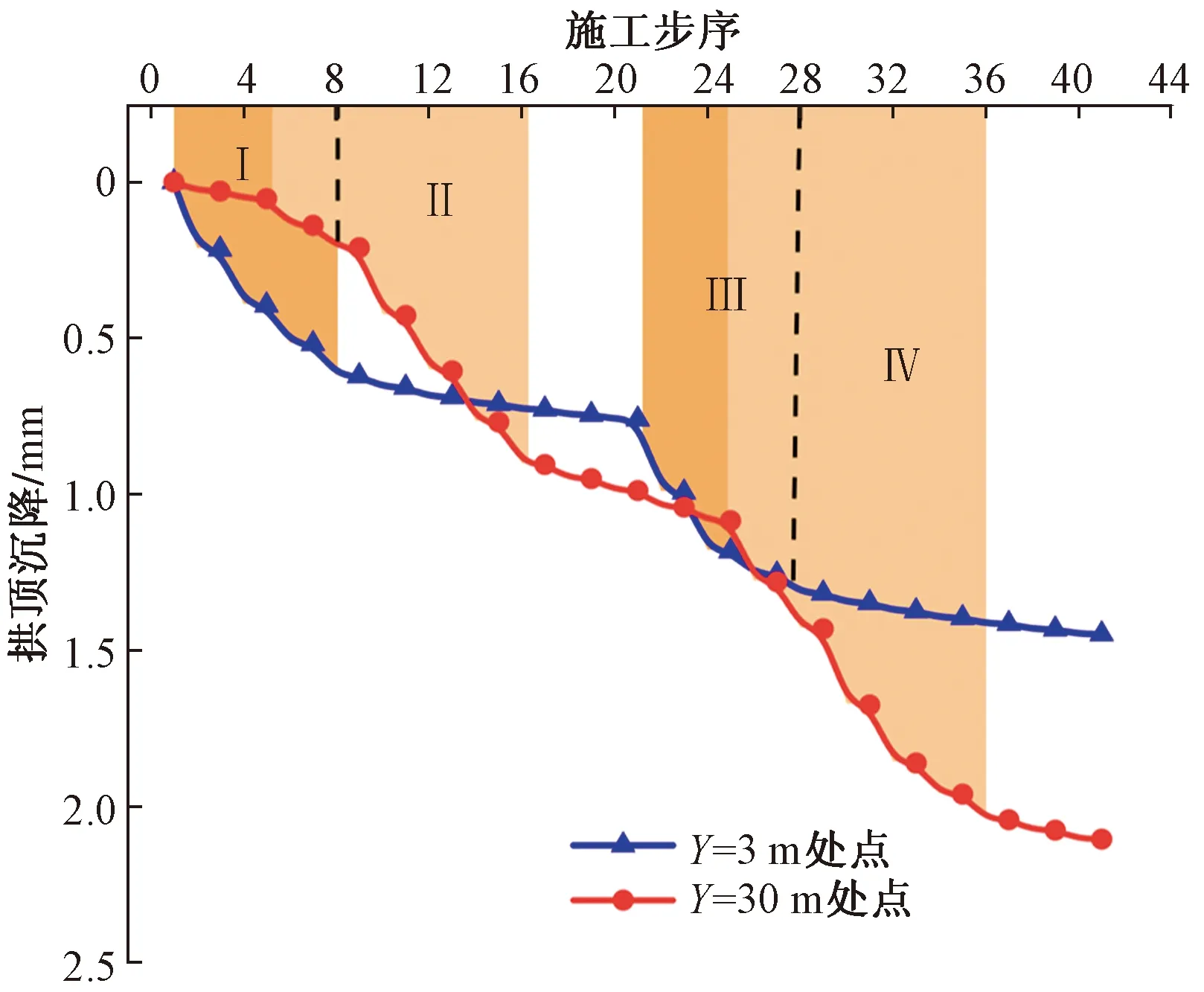
图8 两点拱顶随时间变形变化曲线Fig.8 Deformation curve of two-point vault with time
由图7可知,两点拱底隆起的产生主要集中在部分阶段(图7中Ⅰ、Ⅱ、Ⅲ和Ⅳ阶段)。对于Y=3 m处的点来说,Ⅰ阶段产生的拱底隆起是由于该点所在第一段仰拱被拆除,Ⅲ阶段变形的产生主要由于该点相邻的第二段仰拱被拆除;对于Y=30 m处的点来说,Ⅱ阶段产生变形主要由于第五段仰拱的拆除,Ⅳ阶段的变形主要由于第六段仰拱的拆除,而更换新的C45仰拱的过程对结构的变形影响不大。因此对拱底某点来说,该点的变形主要产生在其所在和相邻段仰拱被拆除的过程中(主要受该点两侧各6 m范围内仰拱拆除的影响),且在该点所在的仰拱段拆除时产生的变形大于相邻段拆除时的变形。随着拆除位置的远离,其余段落的拆除对该点的变形影响越来越小。
由图8可知,与拱底变形产生原因相同,两点(Y=3 m和Y=30 m)对应拱顶位置处的沉降主要在两点所在的仰拱段和两侧的仰拱段拆除的过程中产生(图8中Ⅰ、Ⅱ、Ⅲ和Ⅳ阶段)。而更换新的C45仰拱的过程对拱顶的变形基本没有影响。不同点在于,拱顶的时程变化曲线中阴影部分面积较拱底的更大,说明拱顶某点产生的沉降受到两侧更大范围内仰拱拆除的影响(约为两侧各18 m范围)。随着拆除位置的远离,其余段落的拆除对该点对应拱顶位置处的沉降影响越来越小。
因此,可以根据影响范围来确定在施工中需要进行临时支护的范围,尤其对于病害严重的隧道,其衬砌本身就存在不稳定性,结构可靠度低,这种扰动对相邻隧道衬砌更为明显。为保证在仰拱拆换过程中隧道结构的稳定性,至少应该在仰拱拆除段两侧18 m范围内进行必要的临时加固。
3.3 纵断面变形规律
在仰拱拆换完成时隧道纵断面拱底变形曲线如图9所示。可以看出,仰拱拆换过程中拱底隆起曲线图呈现周期性凸起的形状。在每个6 m拆换段的中点处拱底隆起达到峰值且每个峰值大小基本相同,最大隆起值约为9.27 mm。由上述可知,拱底某点的隆起主要是在该点所在段和相邻段仰拱拆除这两个过程中产生的。在拱底变形产生的第一个阶段,即在该点所在的仰拱段拆除后,由于其两端有未拆的仰拱限制,且在外部围岩的挤压下,可以将每个拆换段拱底各点的连接线(即初支表面)视作两端固定且受均布荷载的梁,在这个阶段的拱底变形呈现出中间部分变形最大、两端变形最小的特征。在变形产生的另一个阶段,即该段的相邻段被拆除,受相邻段的影响,该段的变形整体上会增加但增加量较小,且两端的新增变形量会略大于中间部分,但是新增的变形量不足以改变该段已有向上凸起的变形形状。因此,该段拱底变形整体上呈现出中间大、两边小的形状。在其他段落拆除时,与上述变形产生的过程相同,其他段最终也呈现出中间大、两边小的变形特征,所以隧道拱底的纵断面曲线呈现出不断向上凸起的形状。
第一段和第十段的拱底隆起值较小,是因为这两段变形的受影响范围内有未拆换段,而中间部分段落在相邻两段和自身段拆除时都会产生变形,相比之下,中间部分段的累计变形就会大于两侧6 m的累计变形。在图中也就表现出两侧6 m范围内的拱底隆起值较小。
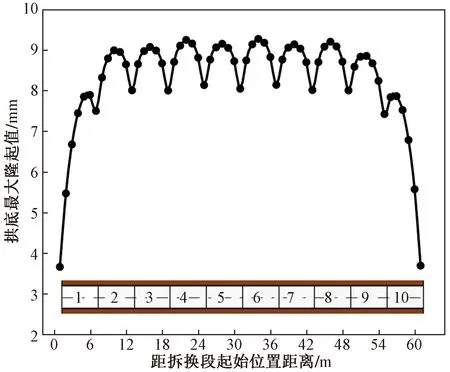
数字1~10为10个拆换段的序号图9 两点拱顶随时间变形变化曲线Fig.9 Deformation curve of two-point vault with time
在仰拱拆换过程中隧道纵断面拱顶变形曲线如图10所示。由于整个拆换段的跨度较大,受两端未拆换段的变形限制,纵断面拱顶沉降曲线不再如监测得到的沉降曲线为一条直线,而是呈现“U”形,整个拆换段两侧的拱顶沉降相对较小,中间段的沉降较大且数值非常接近,拱顶最大沉降达到2.12 mm。由于拱顶各点沉降的受影响范围是两侧各18 m范围,即60 m拆换段的首尾各18 m范围内均受到前或后未拆换段的影响而使得其变形量小于中间部分段,且随着拱顶上点的位置远离未拆换段,该点受到的影响逐渐减小,在图中也就表现出两侧约18 m范围内拱顶沉降逐渐增大。此外,拆换段中间24 m的拱顶各点均受到两侧各18 m范围内仰拱拆换过程的影响,且各点因影响范围内仰拱拆换的产生的最终变形量相同,而与该点的具体位置和产生变形的顺序无关,所以拆换段中间24 m的拱顶最终沉降值基本相同。

数字1~10为10个拆换段的序号图10 拆换段隧道纵断面拱顶变形图Fig.10 Remove and replace longitudinal section of tunnel arch deformation curve
4 拆换顺序对仰拱拆换过程的影响分析
4.1 计算工况
在实际工程中,为了施工的安全性,在仰拱拆换过程中通常会采取跳槽拆换的方式。因此本小节单次拆换距离选取6 m,考虑跳槽拆换不同顺序下隧道结构变形情况。共设置3种拆换工况,如图11~图13所示。
(1)工况一。首先按顺序拆换奇数段的仰拱,在奇数段仰拱拆换完成后对偶数段进行拆换,其中每段仰拱均为先拆换左幅再拆换右幅,如图11所示。
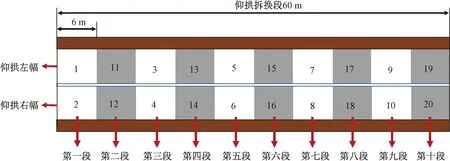
图11 工况一拆换顺序示意图Fig.11 Schematic diagram of removal and replacement sequence in working condition 1

图12 工况二拆换顺序示意图Fig.12 Schematic diagram of removal and replacement sequence in working condition 2
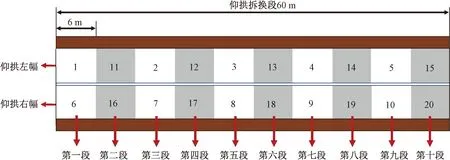
图13 工况三拆换顺序示意图Fig.13 Schematic diagram of removal and replacement sequence in working condition 3
(2)工况二。首先对奇数段左幅仰拱进行拆换,然后对偶数段左幅仰拱进行拆换。在完成全部左幅仰拱的拆换后进行右幅仰拱的拆换,右幅仰拱的拆换也是先拆换奇数段后拆换偶数段,如图12所示。
(3)工况三。首先拆换奇数段仰拱的左幅,然后拆换奇数段仰拱右幅;在完成奇数段拆换后进行偶数段左幅拆换,最后对偶数段右幅仰拱进行拆换,如图13所示。
4.2 拱顶和拱底变形分析
不同拆换顺序下隧道纵断面拱顶沉降曲线如图14所示。与前述拱顶沉降曲线类似,在不同拆换顺序下,拱顶沉降曲线均呈现中间大两边小的特点,且中间段的拱顶位移非常接近。从放大部分可以明显看出3种工况的拱顶沉降值之间的差异,工况一和工况三的拱顶沉降值基本相同,两种工况的曲线分布重合,而工况二的拱顶位移略大于前两者的位移。其中,工况一和工况三在拆换中的拱顶最大沉降值为2.12 mm;工况三的拱顶最大沉降为2.15 mm。
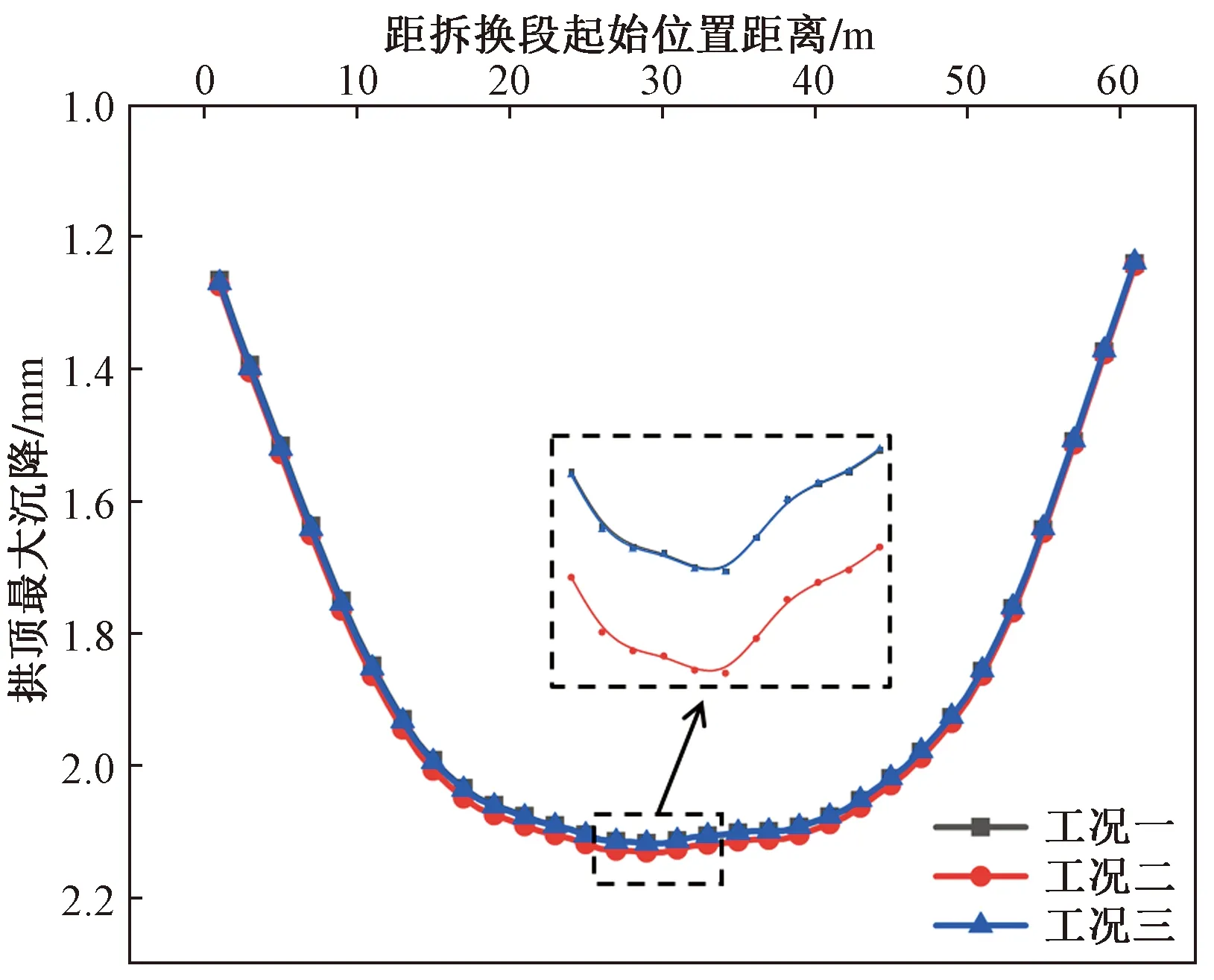
图14 不同拆换顺序下隧道纵断面拱顶沉降曲线Fig.14 Settlement curves of tunnel longitudinal arch under different removal and replacement sequences
不同拆换顺序下隧道纵断面拱底隆起曲线如图15所示。与前述拱底隆起曲线类似,在不同拆换顺序下,拱底的隆起均呈现两端的隆起较中间段小。拱底隆起曲线均呈现周期性向上凸起的形状。周期值为单次拆换的距离6 m,具体原因与前述内容相同。
如图15所示,不同工况比较下,工况一和工况三的拱底位移值基本相同,两种情况的拱底最大位移值分别为9.27 mm和9.30 mm;而工况二的拱底位移值略大于前面两种工况,最大位移值为9.64 mm。
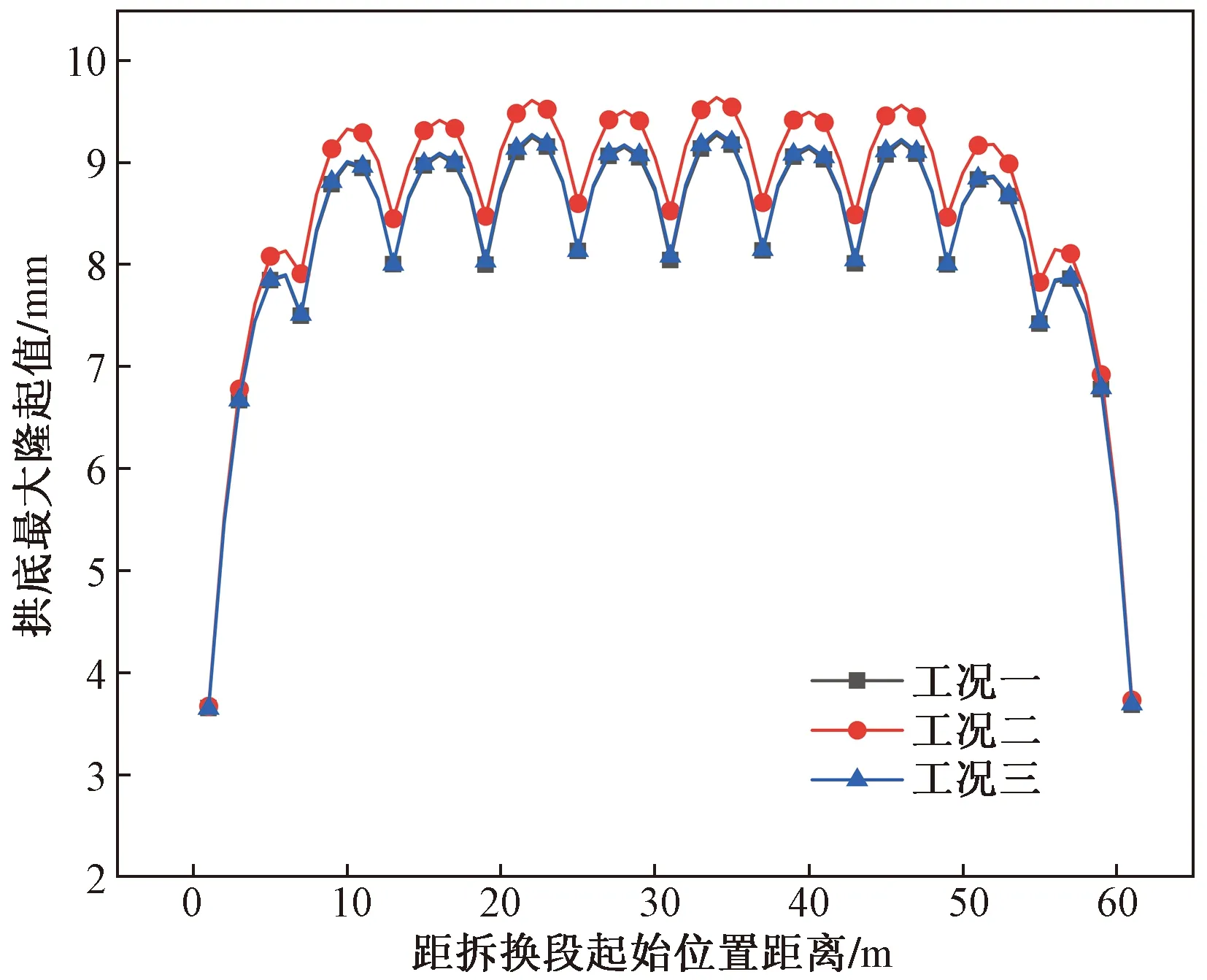
图15 不同拆换顺序下隧道纵断面拱底隆起曲线Fig.15 Heave curves of tunnel longitudinal section arch bottom under different removal sequences
不同拆换顺序下拱顶和拱底的最终变形曲线趋势相同,说明当仰拱拆换采用跳槽拆换方式时,不论采取哪种拆换顺序,最终的拱顶和拱底的变形趋势是相同的,拱顶沉降变形均为“U”字形, 拱底隆起变形均呈周期性向上凸起状。工况一和工况三的拱顶和拱底变形值基本相同,而工况二的拱顶和拱底变形略大于上述两种工况的变形。这就说明虽然工况一和工况三具体的拆换顺序不同,但两种拆换方式实质上是相同的,而工况二的拆换顺序与前两者存在差异。这是由于工况一和工况三在拆除偶数段前已经完成奇数段左右两幅仰拱的拆换,也就是说拆除偶数段时,偶数段相邻两段均为已拆换完成的C45仰拱,能更好地对偶数段拆换过程中产生的位移起到限制作用;而工况二在拆换奇数段左幅仰拱之后,紧接着拆换偶数段左幅仰拱,而右幅仰拱全部处于未拆换状态。
总的来说,工况一和工况三的拆换顺序能及时地使得新筑的更高强度的仰拱闭合成环,能更早地发挥拆换后仰拱的承载能力,使得拱底和拱顶位移也相对较小。因此,在实际工程中,采用跳槽拆换方式时,应遵循使得拆换后的更高强度的仰拱闭尽早合成环的原则,对发挥衬砌结构的承载性能,提高拆换过程中隧道结构的稳定性具有重要作用。
5 拆换距离对仰拱拆换过程的影响分析
拆换距离也是在仰拱拆换过程中对隧道结构稳定性的重要影响因素,而目前实际工程中对拆换距离的确定往往通过经验确定。因此在同一拆换顺序的情况下设置不同的拆换距离来比较不同工况下隧道结构的变形情况。
现有的公路隧道相关规范中对隧道拆换过程中的周边位移和拱顶沉降限值并未做出规定。通过查阅相关文献,魏强[18]对某一铁路隧道仰拱拆换过程中的隧道拱顶沉降监测值提出了分级管理措施,分级管理措施见表2。

表2 隧道结构拱顶沉降监测管理措施Table 2 Monitoring and management measures for vault settlement of tunnel structure
因此,以3 mm为隧道在仰拱拆换过程中的拱顶沉降限值,认为当拱顶沉降在3 mm以内时,隧道结构处于安全状态。
5.1 计算工况
共设置4种单次拆换距离,分别为6 m(0.6D)、8 m(0.8D)、10 m(1D)、12 m(1.2D),其中D为隧道等效直径。拆换顺序为4.1节中的工况一的拆换顺序,如图16所示。
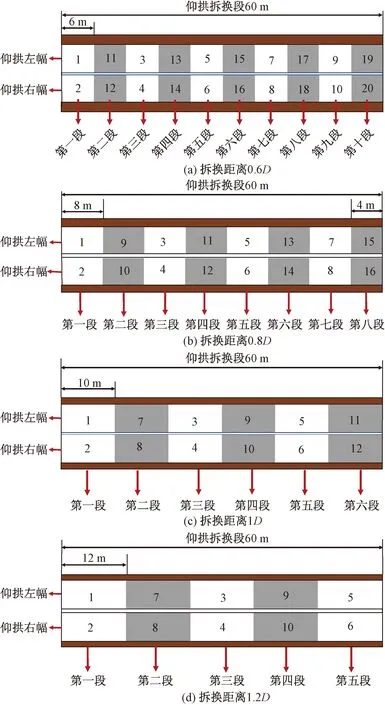
图16 不同拆换距离示意图Fig.16 Schematic diagram of different removal and replacement distances
5.2 结果分析
不同拆换距离下隧道纵断面拱顶沉降曲线如图17所示。由图17可知,随着单次拆换距离的增加,隧道拱顶的沉降值整体都在变大。当单次拆换0.6D时,拱顶的最大位移约为2.11 mm;当单次拆换0.8D时,拱顶的最大位移约为2.27 mm;当单次拆换1D时,拱顶的最大位移约为2.40 mm;当单次拆换1.2D时,拱顶的最大位移约为2.48 mm。
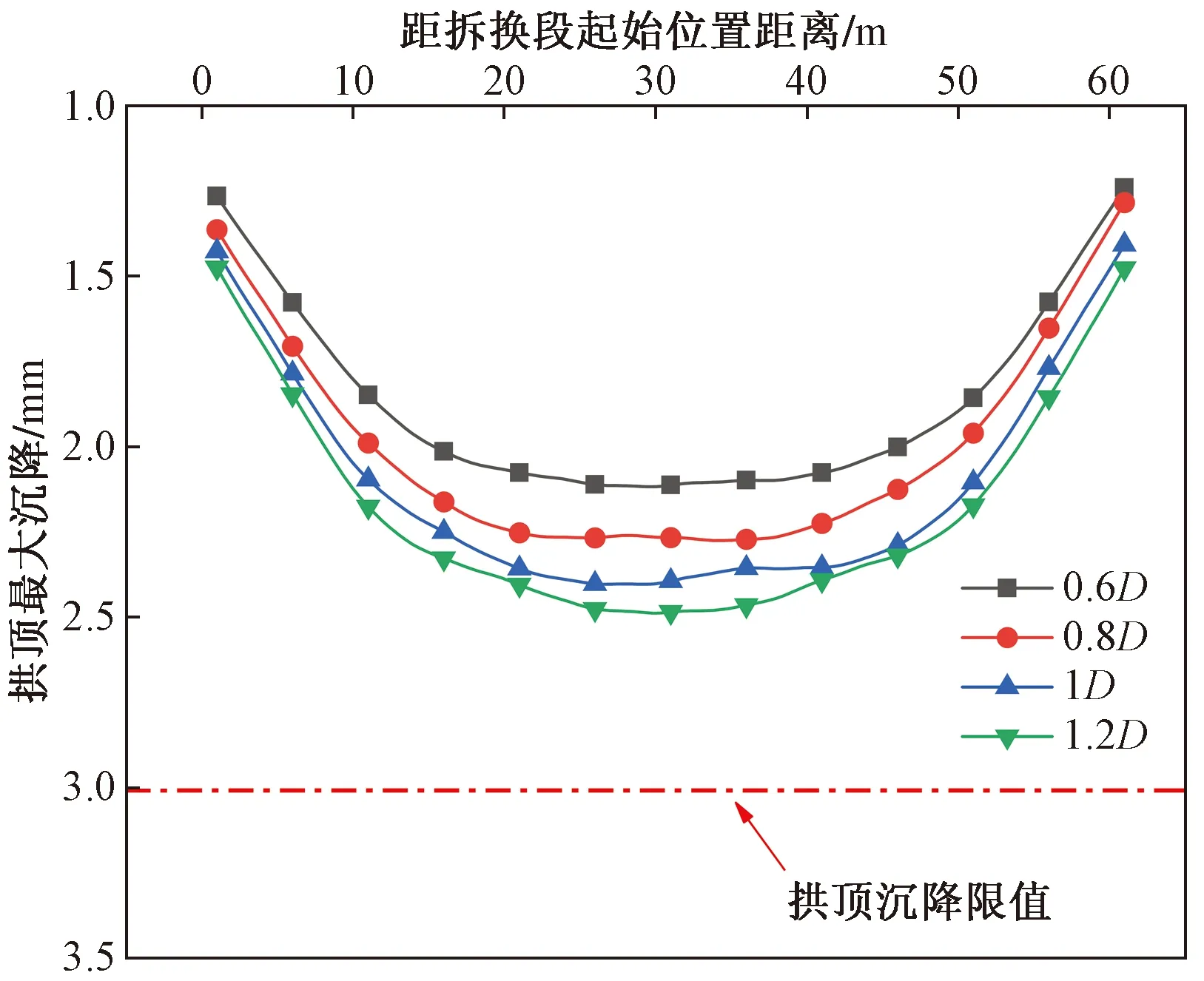
图17 不同拆换距离隧道纵断面拱顶沉降曲线Fig.17 Settlement curve of tunnel longitudinal arch at different removal distances
在不同拆换距离下,拱顶的变形趋势基本相同,都呈现中间大、两边小的特点,且中间段的拱顶位移非常接近。当仰拱拆换距离达到10 m(1D)后,再增加拆换距离时,虽然隧道拱顶的沉降值仍在增大,但是拱顶最大沉降值的增长幅度在减小。可见,当单次拆换距离超过1D并逐渐增加时,仰拱拆换时的隧道结构稳定性受到纵向拆换距离的影响在逐渐减小。
根据4种拆换距离的结果,拱顶产生的位移均小于3 mm。参考上述隧道结构拱顶沉降监测管理措施表,若以拱顶位移3 mm为界限来评价仰拱拆换过程中安全性,当仰拱单次拆换距离小于1.2D时,隧道结构都处于稳定的状态。不同拆换距离下隧道纵断面拱底隆起曲线如图 18所示。由图18可知,随着单次拆换距离的增加,隧道拱底的整体隆起值也在增大。与拱顶最终沉降规律相同,受到两侧的未拆换段的限制,拆换段中间部分的拱底隆起值大于两端的隆起值。在不同的拆换距离情况下,拱底变形趋势也呈现周期性凸起的特点。周期值为单次拆换段的距离,随着单次拆换距离的增加,拱底变形的周期性变化的次数也在相应减小。具体原因与前述原因相同。
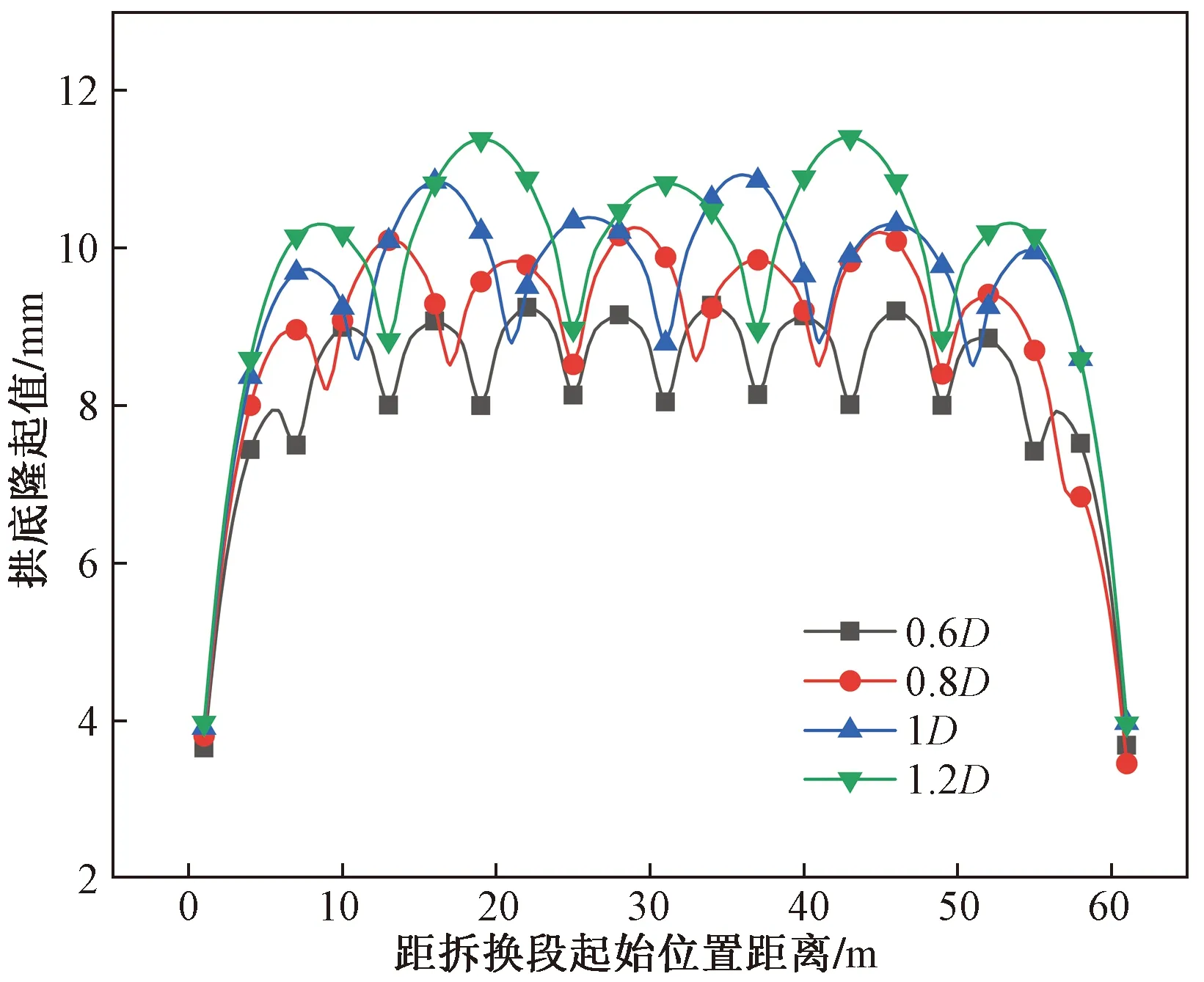
图18 不同拆换距离隧道纵断面拱底隆起曲线Fig.18 Heave curves of tunnel longitudinal section under arch at different removal distances
当单次拆换距离为0.6D时,拱底最大隆起值为9.18 mm;当单次距离为0.8D时,拱底最大隆起值为10.17 mm;当单次距离为1D时,拱底最大隆起值为10.93 mm;当单次距离为1.2D时,拱底最大隆起值为11.38 mm。同样,当拆换距离超过1D后,拱底最大隆起值的增长幅度会变缓,隧道结构的稳定性受到纵向拆换距离的影响减小。
在4种拆换距离中,隧道拱底产生变形值均远大于拱顶产生的变形值,虽然拱顶沉降值处于安全范围内,但考虑到拱底隆起值过大会影响施工,在拆换方案选择时,应该尽可能选择单次拆换距离短的方案以控制拱底变形。
综上,当进行隧道仰拱拆换时,单次拆换距离越大,隧道拱顶和拱底产生的变形就越大。当以隧道拱顶沉降值3 mm为限值时,Ⅴ级围岩情况下,单次拆换距离在0.6D~1.2D时隧道均处于安全状态。但是考虑拱底产生的变形量远远大于拱顶产生的变形量,较大的单次拆换距离会导致拱底的隆起值偏大而影响实际施工,为了将拱底变形控制在较小范围内,应尽量选择单次拆换距离短的方案。
6 结论
通过建立仰拱拆换三维数值模型,分析了不同拆换工况下隧道结构变形规律,主要结论如下。
(1)在仰拱拆换过程中,隧道横截面呈现出向内收缩的趋势,拱脚、拱底和拱顶处容易产生变形,其中以拱底的变形量为最。在实际工程中应注意对上述易变形位置的支护。
(2)拱底和拱顶的变形量会受到其两侧仰拱拆除的影响。如单次拆换距离L=6 m,拱底各点的变形主要是在该点两侧各L(6 m)范围内的仰拱拆除过程中产生,而拱顶各点的受影响范围为该点两侧各3L(18 m)。在实际工程中,由于病害衬砌本身就处于不稳定状态,拆换带来的扰动对其稳定性影响更为明显。因此为保证拆换过程中衬砌结构的稳定,可在每个拆换段两侧各3倍拆换的范围内进行临时加固。
(3)当采用跳槽拆换时,不论拆换顺序如何,最终拱顶和拱底的变形曲线都是相同的,拱顶沉降曲线均为“U”字形;拱底隆起曲线均呈周期性向上凸起状。为减小隧道结构在拆换中的变形,拆换顺序应遵循能够使得新筑仰拱尽早闭合成环的原则,这样有利于发挥更换后的仰拱的承载能力,减小后续相邻段拆换带来的结构变形的影响。
(4)不同的单次拆换距离不会改变拱顶和拱底的变形趋势,但随着拆换距离的增加,拱顶和拱底的变形也相应地增加,增加幅度有所减小。综合考虑到要控制拱底的变形,在实际工程中,应尽量选择单次拆换距离短的拆换方案。

