仿云杉多层环形塔状立体车库结构稳定性

孟杰， 穆永祥， 郭嘉璇， 马孝昌

(太原科技大学机械工程学院， 太原 030024)

近年来，随着经济的增长，汽车数量越来越多。然而城市土地稀缺与日益增长的停车需求之间的矛盾愈演愈烈，所以建设立体车库成为缓解停车难的必然选择。立体车库，又可称为“机械式停车设备”，它是利用机械和电气系统组成的，用来存取车辆的设备。具有占地少、停车多、投资少、停车方式先进等优点。然而在实际运行过程中，随着容车量的增加，立体车库结构承受的拉力或压力也随之增大，容易发生失稳，造成车辆损坏，甚至人员伤亡。 因此，分析立体车库结构的稳定性是十分必要的。目前国内外对立体车库结构稳定性的研究主要如下。

文献[1-6]研究的是巷道堆垛式立体车库。从模态、静力、动力和地震反应谱等方面分析了单侧堆垛式立体车库钢结构有限元模型，结果表明结构强度可以抗八级风和七级地震；针对公交车停车难问题，设计了巷道堆垛式立体车库结构及控制系统，探究了多种搬运方式下的存取策略；在实现低能耗和低时耗方面，通过遗传算法，优化了集束搜索，进而改进了堆垛机运行路径。

文献[7-10]研究了垂直升降式立体车库。针对钢架结构类车库，分析了其在升降过程中受到冲击激励的响应，发现结构振动最大值出现在提升过程的加速度阶段且与速度模式有关，并根据冲击速度、轴向载荷和冲击高度的不同，设计了柱的结构，以提高结构稳健性；并结合可编程逻辑控制器等技术对车库控制系统进行了优化，提高了车库结构强度和存取效率。

文献[11-13]对地下立体车库进行了研究。通过优化满载情况下环井式地下立体车库钢结构模型，有效降低了结构的最大变形量和最大等效应力；针对地下圆柱形车库结构，提出一种新的梁柱节点分布形式，通过减小连接梁的截面和基础柱的厚度，改善节点的静力性能和抗震性能；为提高地下式立体车库搬运装置的运行效率，设计了一种夹持式停车搬运器，实现了停车设备高度自动化。

文献[14-15]分析了平面移动式立体车库。从静力与动力学两方面研究钢结构的高层平面移动式立体车库，并且利用果蝇算法和遗传算法优化了存取车调度系统，提高了车库运行效率，减少了运行能耗。

文献[16-17]分析研究了新型立体车库。探究了九宫格式立体车库静力、模态和随机振动情况；并验证了智能环形叠放立体车库可以在承受复杂负载条件下有效地进行存取车辆。

综上所述，目前研究集中于已有几种类型的立体车库结构，分析车库整体或部分结构在外界载荷作用下的稳定性，或利用算法对存取车调度进行优化等。现有的立体车库虽提高了空间利用率，但失稳现象仍然存在。所以车库结构稳定性仍有待提高。经过长期自然进化的生物具有优异的性能，模仿生物构造和功能的发明与尝试是开辟新技术的主要途径之一。然而从仿生学角度将生物结构应用于立体车库以提高结构稳定性的研究甚少。

云杉由主干和若干侧枝构成，整体呈多层塔状。其结构稳定且具有优良的抗冲击性能。因此，将云杉优良的稳定结构应用于立体车库，是一种提高立体车库稳定性的有效途径。现从仿生学的视角切入，以生物学为理论基础，抽象出云杉生物模型，构建仿云杉多层环形塔状结构，结合工程实际受力特点，设计一种新型仿云杉多层环形塔状结构升降式立体车库，探究仿生车库结构的稳定性。

1 云杉多层环形塔状结构研究

1.1 生物模型建立

云杉属于松科类植物(如图1所示)，多生长在寒冷多风的环境中，可承受强烈的风雪载荷。

图1 云杉实际结构Fig.1 Actual structure of spruce

云杉为典型的单轴分枝植物，其由一根截面为圆形的主干和若干侧枝构成，主干根部横截面直径最大，顶部横截面直径最小，从主干根部到顶部直径按线性减小，主干作为承受大部分载荷的结构，不仅要承受自身的重量，还要承受风雪载荷的作用。云杉的侧枝包括二级枝干和枝叶，沿主干轴向每隔一段距离就会有若干侧枝伸出，二级枝干横截面为圆形，沿枝干伸展方向，直径按线性减小，二级枝干离地面越远，其长度越小，侧枝在忽略重力作用造成弯曲的影响下，可以看作在同一平面内。

云杉主干受力特点类似悬臂梁，受到风雪载荷时可以承受较大的弯矩，因此其主干可以简化为底层最宽、从下到上缓慢变细的悬臂梁结构。主干同一水平位置处的侧枝在同一平面内，有明显的分层现象，而且沿主干轴向各层伸出的长度逐渐减小，在总体结构上呈现为塔状，如图2和图3所示。

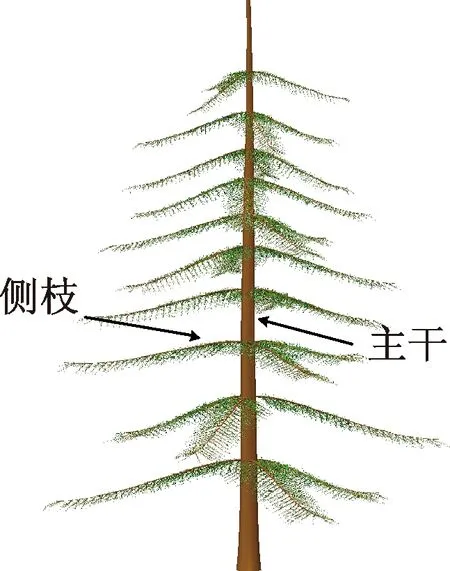
图2 生物模型Fig.2 Biological model

图3 结构等效模型Fig.3 Equivalent model of structure

1.2 立体车库结构设计

以生物结构力学性能为基础，将生物结构进行简化，构建云杉多层环形塔状结构，根据立体车库受力特点将多层环形塔状结构和升降式立体车库中的每个结构相融合。仿生立体车库的主体结构主要抵抗外荷载，与云杉的树干相对应，整体呈现为圆形截面的悬臂梁，其底部直径最大，沿轴向向上其直径线性减小。云杉主干轴向同一位置的侧枝在同一水平面内，组成类似环形平面，其外径沿主干轴向越来越小。因为侧枝可以承载积雪，所以环形平面可作为仿生立体车库的载车结构，其外径沿主体结构轴向向上逐渐减小，呈现为变径环形载车结构，仿生立体车库的结构模型如图4和图5所示。

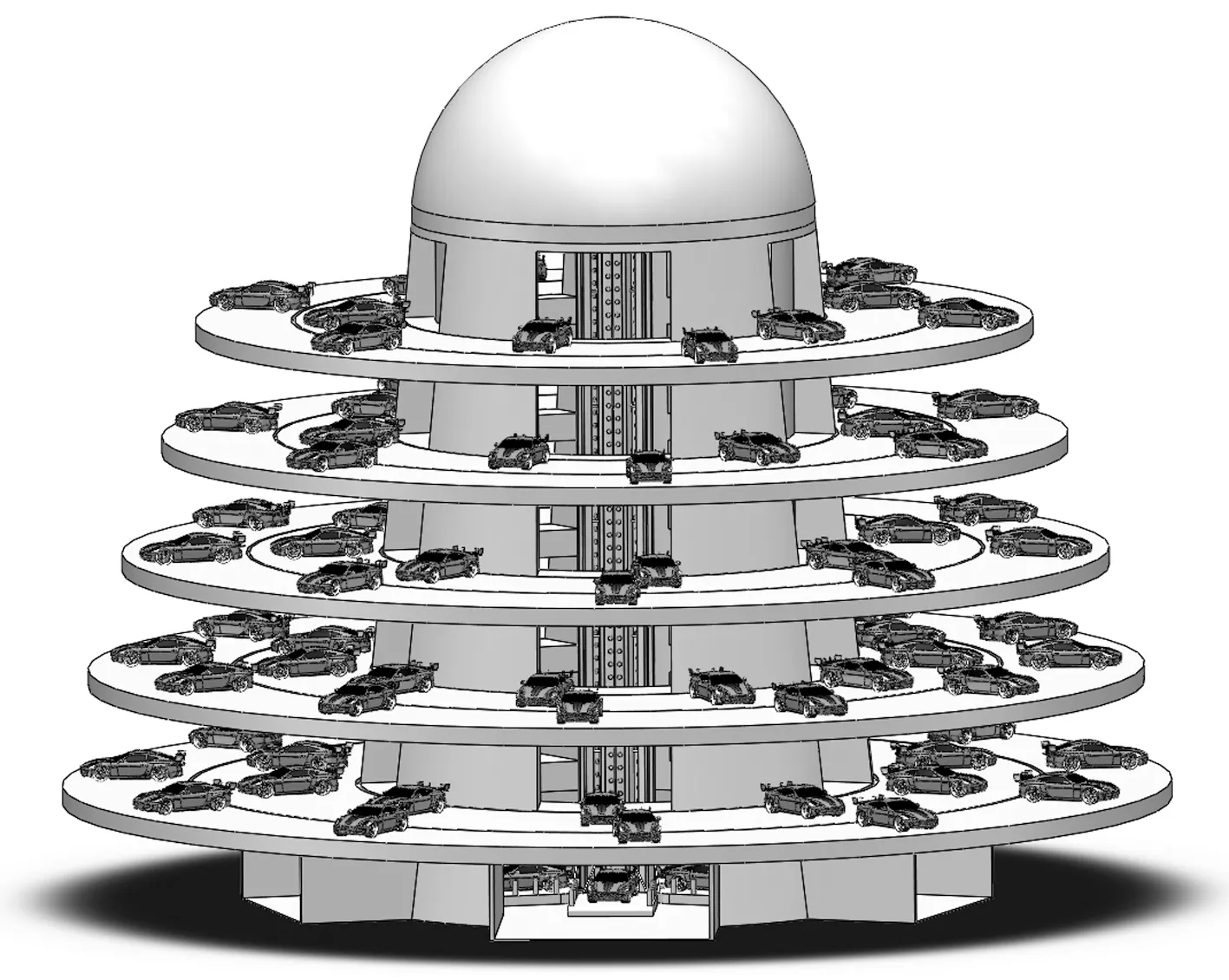
图4 仿生立体车库结构Fig.4 The structure of bionic stereo garage

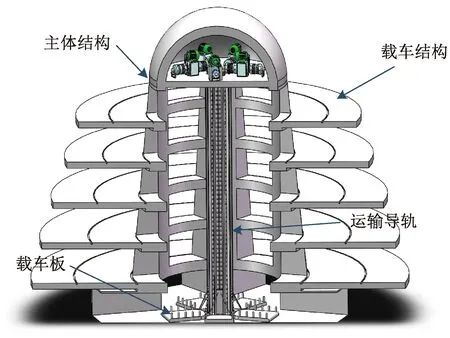
图5 仿生立体车库剖面结构介绍Fig.5 The section structure introduction of bionic stereo garage

直筒型立体车库主体结构的直径沿轴向不变，呈现为横截面为圆形的等截面悬臂梁，环形平面作为直筒型结构立体车库的载车结构，其内外径沿主体结构轴向均不变，呈现为等径环形载车结构，直筒型立体车库的结构模型如图6和图7所示。

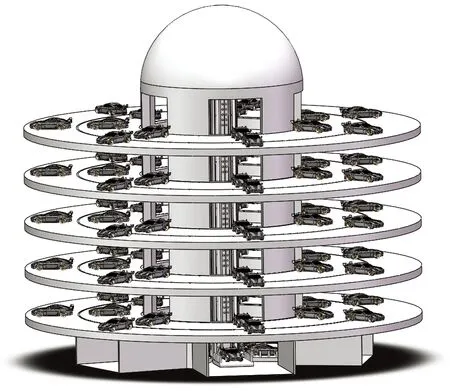
图6 直筒型立体车库结构Fig.6 The structure of straight cylindrical stereo garage

图7 直筒型立体车库结构介绍Fig.7 The introduction of straight cylindrical stereo garage

2 立体车库结构分析

2.1 立体车库力学模型

根据立体车库中主体结构以及内部运输通道的整体尺寸，载车结构的位置，层数和每层停放汽车的总质量，将车库整体结构简化为有五个集中质量和六段无质量,有长度和抗弯刚度梁的五自由度系统(如图8所示)。将一个集中质量和一段梁归为一个单元，各个集中质量在梁上的位置为各层载车结构在主体结构上所在位置。

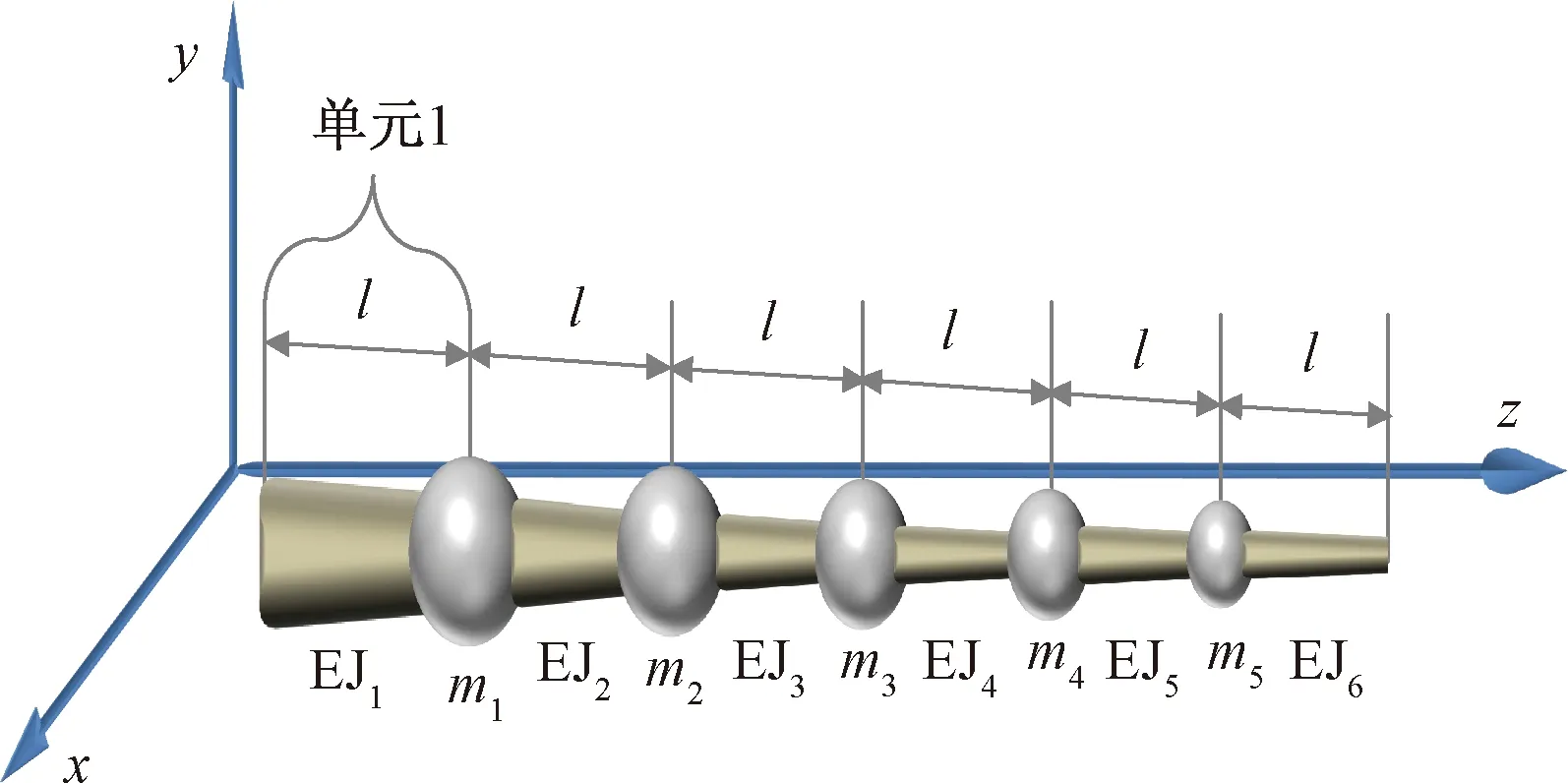
EJi为第i段无质量梁的弯曲刚度；l为梁的长度；mi为第i个集中质量图8 多自由度系统Fig.8 Multiple degrees of freedom system

设状态矢量表达式为

(1)

式(1)中：y为位移；θ为转角；M为弯矩；Q为剪力。

第i段无质量梁进行受力分析如图9所示，从受力分析中建立力和力矩的平衡条件为

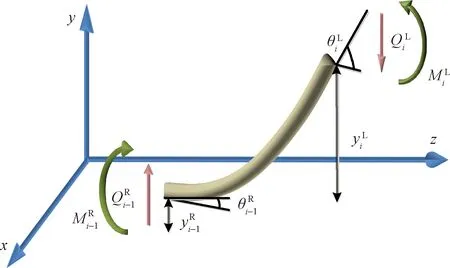
图9 无质量梁受力分析Fig.9 Stress analysis of massless beam

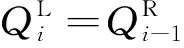
(2)

(3)

根据材料力学中挠曲线方程建立梁两端关于位移y和转角θ的关系为

(4)

(5)

将式(2)～式(5)合写为矩阵形式为

(6)

(7)

第i个集中质量进行受力分析如图10所示，从受力分析中建立力和力矩的平衡条件如下。

图10 集中质量受力分析Fig.10 Stress analysis of concentrated mass

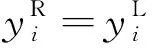
(8)

(9)

(10)

(11)

将式(8)～式(11)合写为矩阵形式为

(12)

(13)

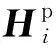
(14)

式(14)中：Hi为第i个单元的传递矩阵。

通过各单元的传递矩阵，就可以得到多自由度系统最左端与最右端的状态矢量间的传递关系[18]。

在仿生立体车库和直筒型立体车库的多自由度系统中，因为两种结构中环形载车结构间的距离相同，所以式(2)～式(13)中无质量梁的长度l均相等。由于仿生立体车库的主体结构为变截面悬臂梁，因此式(2)～式(13)中各层横截面对中性轴的惯性矩不相等，而且沿轴向离地面越远，惯性矩越小；而直筒型立体车库中，主体结构为等截面悬臂梁，因此式(2)～式(13)中各层横截面对中性轴的惯性矩相等。

2.2 系统固有频率和主振型

用传递矩阵法根据边界条件建立频率方程[19]，通过求解频率方程得到各阶固有频率以及主振型。

根据各个单元间的传递矩阵，可以得到悬臂梁最左端和最右端状态矢量的关系为

Z6=HZ0

(15)

将式(15)中传递矩阵和状态矢量展开可得

(16)

式(16)中：hij为传递矩阵H中对应位置的元素。

悬臂梁两端的边界条件为

(17)

将悬臂梁边界条件代入式(17)可得

(18)

由于悬臂梁固定段M0、Q0不全为零，据此可得频率方程为

(19)

求解式(19)可得到多自由度系统各阶固有频率。利用各单元传递矩阵式(14)可以得到各个集中质量的状态矢量，将各阶固有频率代入状态矢量，取各个集中质量状态矢量的第一个元素组成了相对应固有频率下的主振型。

2.3 系统对激励的响应

当汽车停放在载车结构上时，对载车结构产生的激励实为脉冲激励，脉冲激励的效应使与载车结构相对应的集中质量获得初速度为

(20)

式(20)中：I0为载车结构受到的冲量。

但在停放车辆这一瞬时，载车结构位移来不及改变，因此相对应的集中质量位移关系为

x(0+)=x(0-)=0

(21)

因为这一脉冲作用时间很短，此后，系统即做自由振动。

做如下主坐标变化，对位移方程进行解耦得

x=Apxp

(22)

式(22)中:Ap=[A(1)A(2)A(3)A(4)A(5)]为主阵型矩阵,A(i)为第i阶振型矩阵。

则主坐标下的运动方程为

(23)

式(23)中：Mp为主质量矩阵；Kp为主刚度矩阵；Mp、Kp均为对角矩阵。

当车库第一层载车结构停放车辆时，多自由度系统中的第一集中质量获得初始条件，对初始条件进行主坐标变化可得

(24)

xp(0)=[A(i)]TMx0/Mi

(25)

将主坐标下的初始条件代入运动方程求解可得主坐标下多自由度系统的响应，对主坐标下的响应进行变化，即可得到系统对外界激励的响应，公式为

x=A(1)xp1+A(2)xp2+…+A(i)xpi

(26)

式(26)中：xpi为第i阶主坐标下的响应。

3 立体车库数值分析

立体车库为混凝土结构，取C30混凝土，弹性模量为E=3×104MPa，结构总体高度为15.2 m，分为五层，每层间距2.2 m，主体结构中间的运输通道为直筒型通道。仿生立体车库和直筒型立体车库整体尺寸如图11和图12所示。

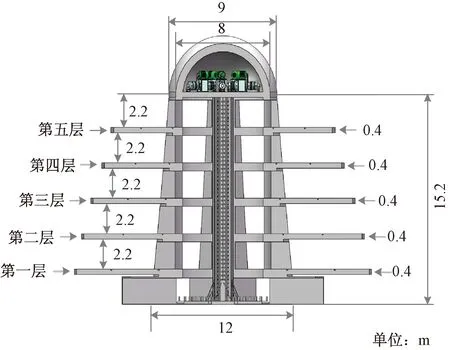
图11 仿生立体车库整体尺寸Fig.11 The overall size of bionic garage

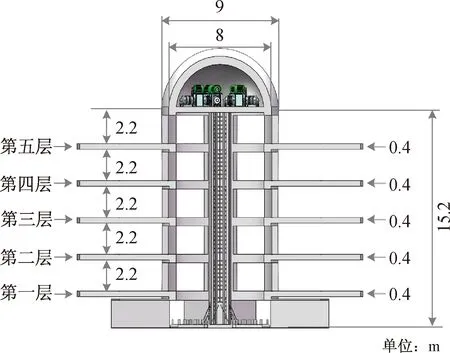
图12 直筒型立体车库整体尺寸Fig.12 The overall size of straight cylindrical garage

仿生立体车库各层载车结构承载能力不同，设置第一层载车结构满载时的质量m1=425 246 kg[20]，当所有载车结构满载时，各层载车结构质量依次满足m2=0.9m1、m3=0.8m1、m4=0.7m1、m5=0.6m1比例关系。而直筒型立体车库由于各层载车结构承载能力相同，因此各层载车结构满载时质量相等，设置每层满载时的质量为385 246 kg[21]。

将数据代入式(1)～式(19)计算可得仿生立体车库的方程为

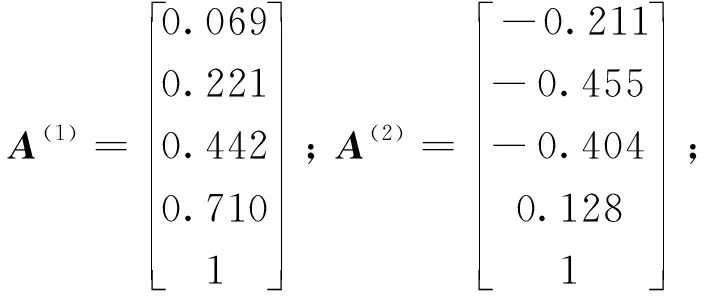
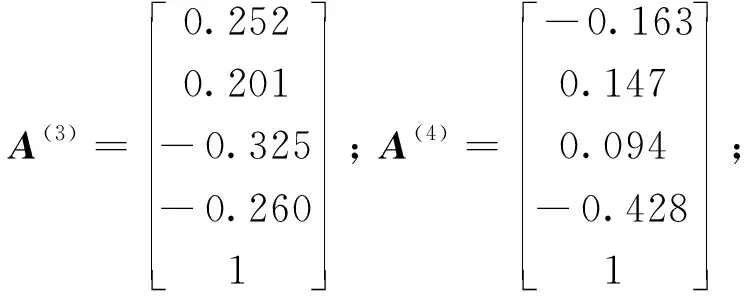
ω1=1.929×102rad/s;ω2=1.014×103rad/s;ω3=2.848×103rad/s;ω4=5.989×103rad/s;ω5=1.048×104rad/s。

式中：A(1)、A(2)、A(3)、A(4)、A(5)分别为第一阶至第五阶主振型，ω1、ω2、ω3、ω4、ω5分别为第一阶至第五阶固有频率。

4 结果对比分析

经过式(22)～式(26)计算分析系统对外界激励的响应。

两种结构立体车库的振动位移频谱分析如图13所示。可以看出，直筒型立体车库第一至第五阶固有频率均小于仿生立体车库，各层载车结构的各频率对应的位移幅值随离地面距离的增加而增大。不仅如此，一阶频率对应的位移幅值也随离地面距离的增加增大，且一阶固有频率对应的位移幅值占结构位移幅值的比例逐渐增大。

图13 位移频谱分析图Fig.13 The diagram of displacement spectrum analysis

两种结构立体车库的五层载车结构的位移如图14～图18所示，速度如图19～图23所示。

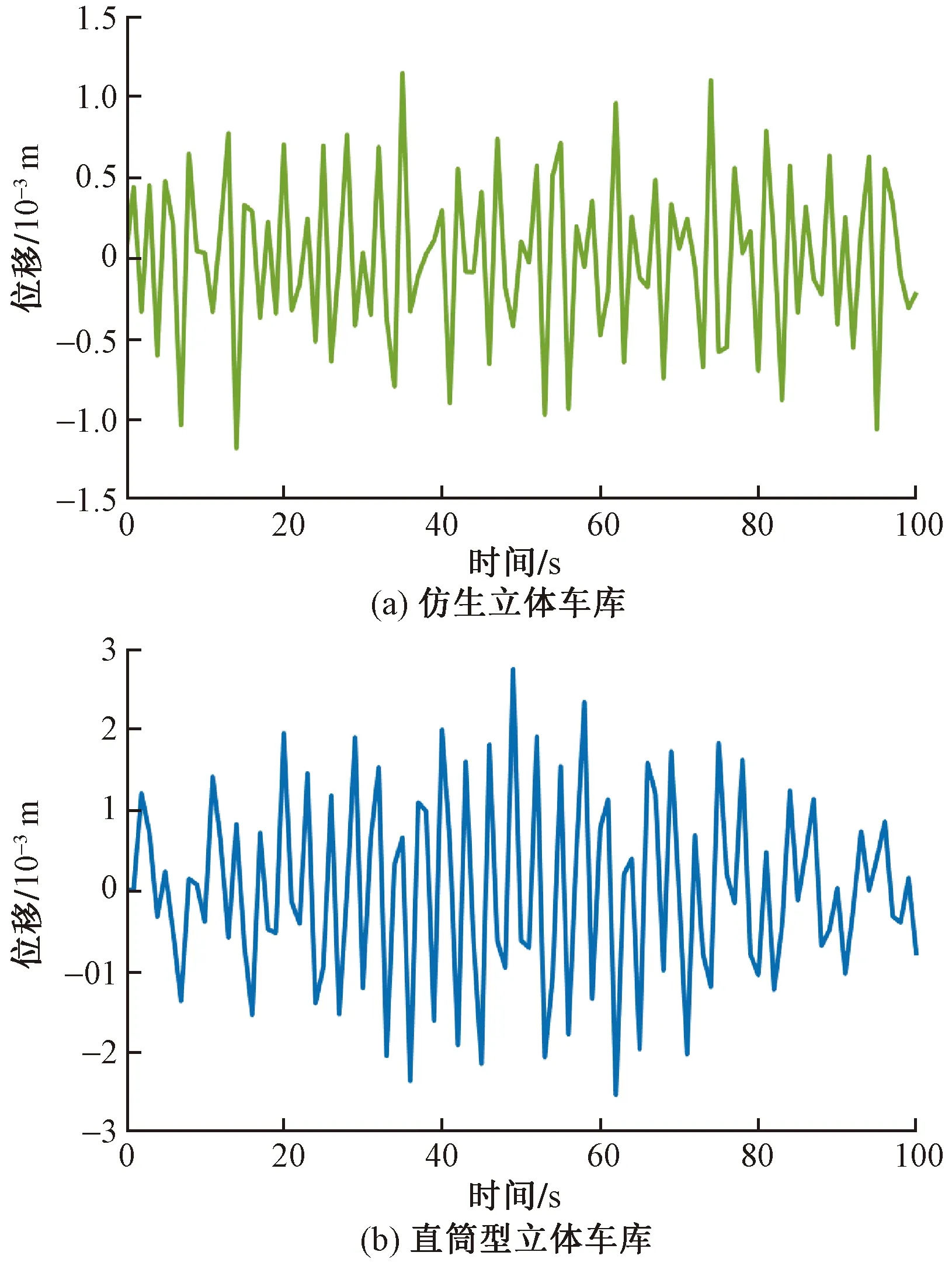
图14 第一层载车结构位移Fig.14 Displacement of the first parking equipment

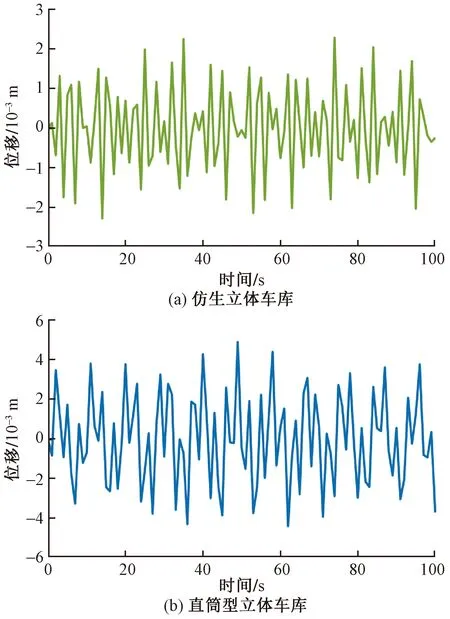
图15 第二层载车结构位移Fig.15 Displacement of the second parking equipment

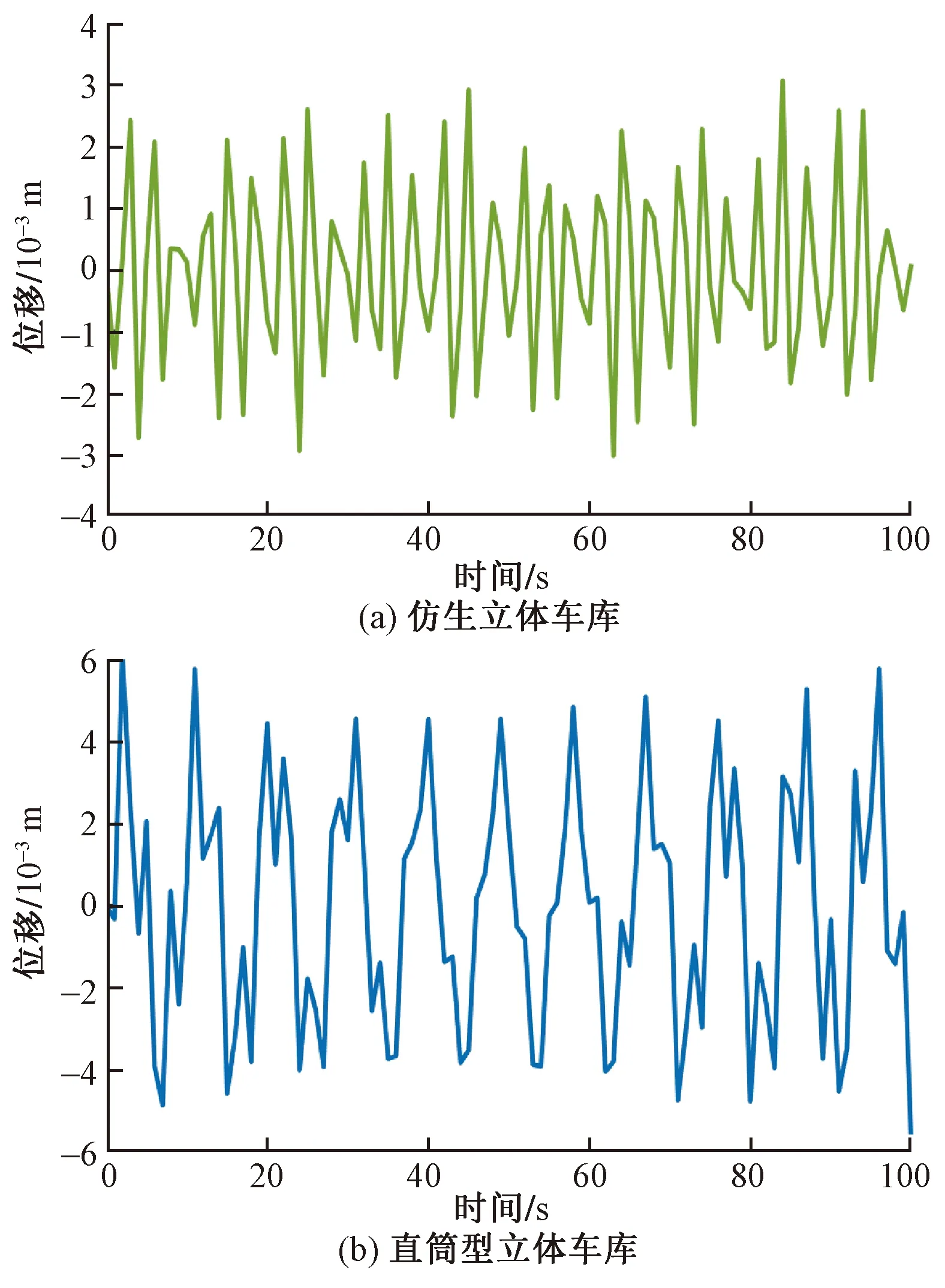
图16 第三层载车结构位移Fig.16 Displacement of the third parking equipment

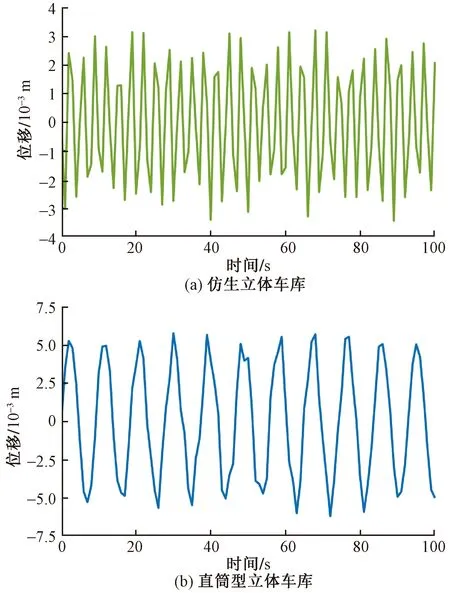
图17 第四层载车结构位移Fig.17 Displacement of the fourth parking equipment

图18 第五层载车结构位移Fig.18 Displacement of the fifth parking equipment

由图14～图18可知，两种结构立体车库的第一层载车结构受到外界激励时，各层载车结构的位移振幅变化趋势相同，第一层载车结构位移振幅均最小，沿轴向离地面越远，其他载车结构的位移振幅逐渐增大。两种结构立体车库的各层载车结构位移振幅变化趋势虽然相同，但位移标准差却不相同，仿生立体车库各层载车结构位移标准差都要明显小于直筒型立体车库相对应的载车结构位移标准差。

由图19～图23可知，两种结构的第一层载车结构受到外界激励时，各层载车结构的速度幅值变化趋势相同，第一层载车结构速度的幅值均最小，沿轴向离地面越远，其他载车结构的速度幅值逐渐增大。两种结构立体车库的各层载车结构速度幅值变化趋势虽然相同，但速度标准差却不相同，仿生立体车库各层载车结构速度标准差都要明显小于直筒型立体车库相对应的载车结构速度标准差。

图19 第一层载车结构速度Fig.19 Velocity of the first parking equipment

图20 第二层载车结构速度Fig.20 Velocity of the second parking equipment

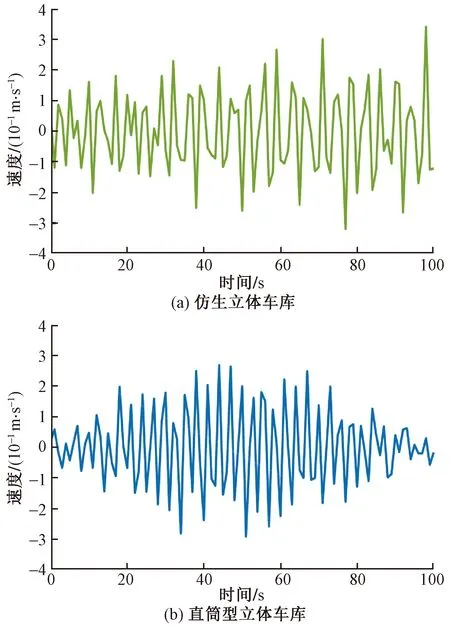
图21 第三层载车结构速度Fig.21 Velocity of the third parking equipment

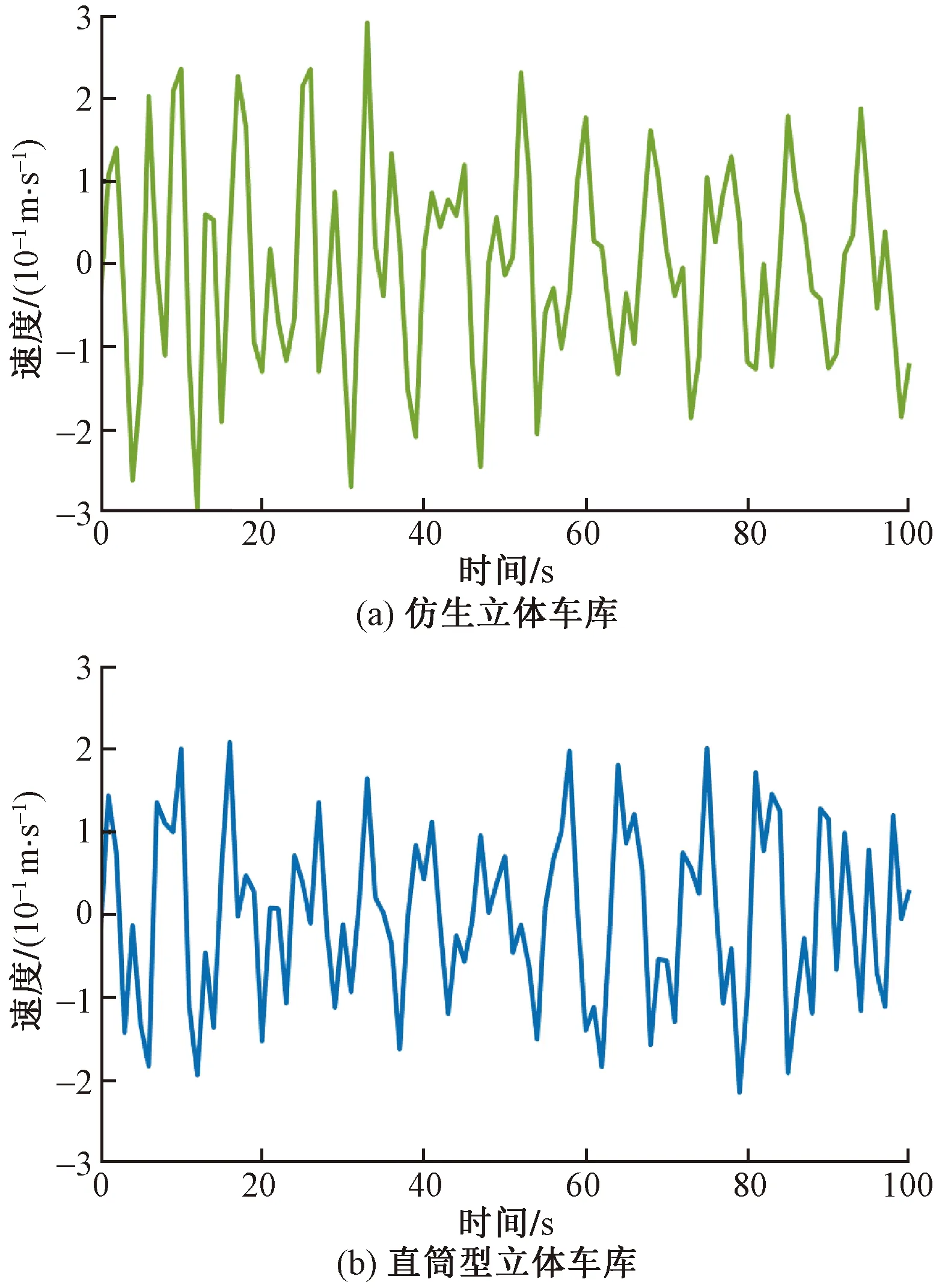
图22 第四层载车结构速度Fig.22 Velocity of the fourth parking equipment

图23 第五层载车结构速度Fig.23 Velocity of the fifth parking equipment

分析表1～表4可知，两种结构立体车库的第一层载车结构受到脉冲激励时，仿生立体车库第一层载车结构位移、速度的标准差相较直筒型立体车库第一层载车结构位移、速度的标准差分别降低了61.98%、42.10%；第二层分别降低了65.51%、45.51%；第三层分别降低了71.11%、43.50%；第四层分别降低了75.42%、27.20%；第五层分别降低了71.46%、24.14%。

仿生立体车库中，其主体结构底层最宽，沿轴向其截面直径线性减小，式(2)～式(13)中的抗弯刚度会随主体结构上各位置截面直径的变化而变化，因为主体结构底层最宽，所以其抗弯刚度最大，其余各位置抗弯刚度沿轴向向上逐渐减小；直筒型立体车库因其主体结构各位置直径不变，因此其各个位置抗弯刚度均相等。在经过式(7)场传递和式(13)点传递后，仿生立体车库在底层产生的挠度相较于直筒型立体车库会小很多，传递到结构上层的挠度也会小很多，因此，其各层载车结构的位移，速度变化也很小。

数值分析与公式计算均说明仿生立体车库底层变形和振动最小，底层传递到上层的变形和振动也会逐渐减小，结构整体更稳定。

表1 仿生立体车库位移响应Table 1 Displacement response of bionic stereo garage

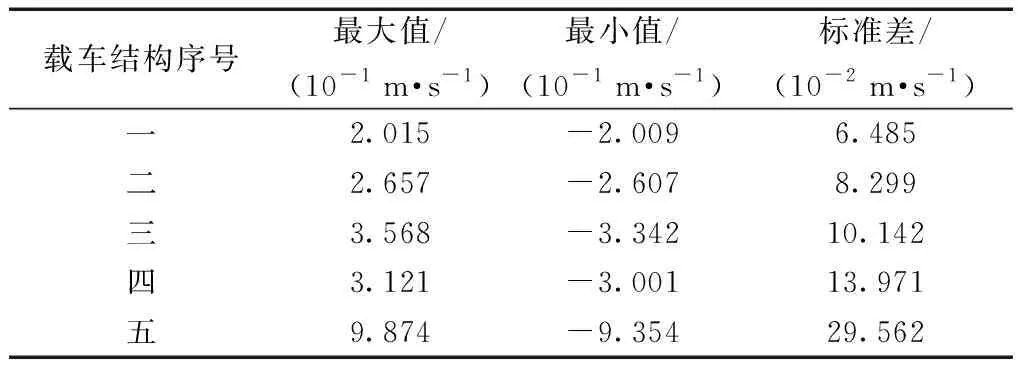
表2 仿生立体车库速度响应Table 2 Speed response of bionic stereo garage

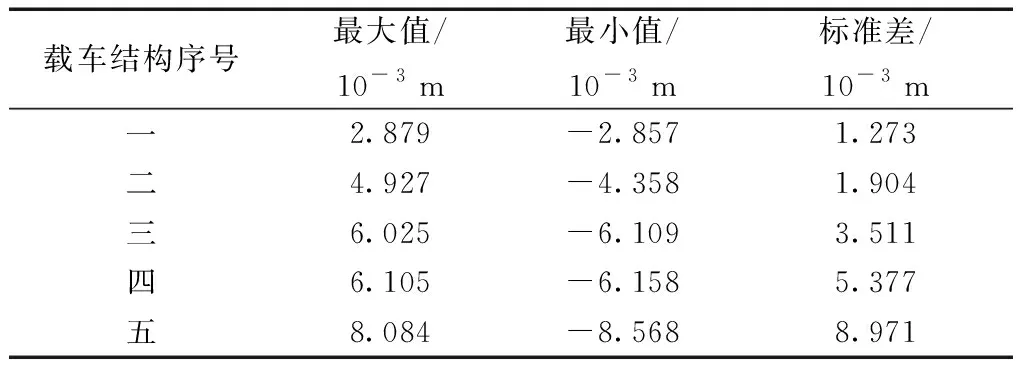
表3 直筒型立体车库位移响应Table 3 Displacement response of a cylindrical stereo garage

表4 直筒型立体车库速度响应Table 4 Speed response of a cylindrical stereo garage

5 结论

以生物学为基础，将云杉优良的结构应用于立体车库，以提高其稳定性，通过公式计算和数值模拟对比仿生立体车库和直筒型立体车库的激励响应可得出以下结论。

(1)直筒型立体车库第一至第五阶固有频率均小于仿生立体车库，各层结构的频率对应的位移幅值随离地距离呈递增趋势，且总位移幅值中一阶固有频率对应幅值的占比随离地距离逐渐增大。

(2)相较于直筒型立体车库，仿生立体车库从底层传递到上层结构的变形与振动更小；在相同轴向位置处，仿生立体车库产生的变形与振动都要明显小于直筒型立体车库。

综上可知，仿云杉多层环形塔状结构立体车库结构更加稳定。