富水黏土地层盾构隧道开挖面稳定性

刘腾， 狄启光， 李鹏飞， 王帆， 邹鸿浩

(1.北京市政建设集团有限责任公司， 北京 100048； 2.北京工业大学城市与工程安全减灾教育部重点实验室， 北京 100124)

随着中国经济的不断发展，中国的现代基础设施建设水平已经走在了世界前列。但随着城市化进程的不断推进，人口集中且流动性大，城市化的进一步发展越来越受到交通系统的制约，为解决这一突出问题，越来越多的城市获批兴建城市轨道交通[1]。盾构法由于具备安全、快速、高效、施工影响小等优点，被广泛应用于城市地下隧道的施工中。盾构在施工过程中通过控制开挖面的支护力来控制开挖面的稳定性，过大或者过小的支护力都会引起开挖面失稳[2]。盾构开挖面稳定性研究一直作为隧道研究的热点问题，研究热点也一直聚焦在合理的破坏模式的假定、准确的极限支护力的计算两个方面。

极限平衡法最早被用来分析边坡的稳定性以及地基承载力的计算，由于极限平衡法具有原理简单、计算方便等优点，一些学者将其应用于隧道开挖面稳定性的研究中。Zhang等[3]提出了考虑水平土拱效应的对数螺旋模型。Yu等[4]给出了适用于成层土的三维楔形体模型。为进一步研究大直径矩形顶管开挖面稳定性，Chen等[5]在提出的侧向应力比的基础上改进了楔形体模型。丁万涛等[6]提出了矩形截面主动极限支护压力的计算方法。与极限平衡法类似，极限分析法最早用于土坡稳定性的分析,后被相关学者应用到开挖面稳定性的研究中。Soubra等[7-8]在隧道顶部的刚性锥体和隧道前方的刚性锥体之间，新加入了一个由无限个顶角的小圆锥体互相截取构成的剪切体。随后对前述破坏机制进一步改进，提出了一种由五个刚性截锥体组成的新的三维锥形体破坏机制。基于空间离散技术，Mollon等[9]提出了三维牛角状的破坏模式，进一步提高了极限支护力的求解精度。宋春霞等[10]针对隧道开挖面与计算模型接触处为不完全接触的问题，给出了一种新的适用于纯黏土地层的破坏模式，同时避免了Mollon等[9]的空间离散技术计算过程复杂的缺陷。计算模型通过对三维破坏模式进行改进，利用编程优化进行求解。结合数值模拟，Zhang等[11]提出了一种新的计算模型，适用于计算浅埋圆形隧道的开挖面极限支护力。假定隧道拱顶上方土体质为非匀质地层，Han等[12]提出了一种新的三维破坏机制所示。Li等[13]为了分析不排水条件下盾构隧道开挖面稳定性，根据多椎体破坏模式进行创新。一些学者采用有限元[14-18]、有限差分[19-20]以及离散元[21-22]等数值模拟方法研究了无水地层盾构开挖面失稳破坏问题。缩尺模型试验[23-25]与离心模型试验[26-29]模型试验被广泛开展以更加直观地探索开挖面前方破坏模式。

上述文献均是针对无水地层开展的研究。Li等[30]基于所提出的二维水头分布方程，研究了渗流条件下的开挖面稳定性。Liu等[31]通过简化的水头分布方程和极限分析方法分析了地下水渗流对成层土盾构隧道开挖面稳定性的影响。Pan等[32]根据极限分析和由数值模拟结果插值所得孔隙水压力，研究了孔隙水压力对掌子面的影响。 Lee等[33]提出了采用数值模拟中获得平均水压力的方法。此外，部分学者基于极限平衡法和通过插值或简化水头解析方程对得到的水头进行了研究[34-35]。离心模型试验[36-37]也是研究渗流对掌子面稳定性影响的重要方法。

然而，有关黏土地层盾构隧道开挖面稳定性的研究很少。在深埋富水黏性土地层中，适用于计算开挖面稳定性的理论方法与数值模拟分析存在较大的差距，需要进一步展开研究。现开展不排水地层的数值模拟；研究开挖面极限支护力以及破坏区范围随着变量变化的规律；之后，根据不排水黏性土的离心试验，结合功率分析得到开挖面极限支护力修正系数，并将修正后的极限支护力与相关研究进行对比，进而将研究成果应用于实际工程。以期为富水黏土地层盾构隧道的工程实践提供借鉴与指导。

1 数值模拟

1.1 计算模型

FLAC3D数值模拟软件广泛用于岩土工程的研究中，为分析隧道不排水效应下的开挖面失稳破坏，采用 FLAC3D软件研究深埋富水黏土地层中，盾构隧道在不排水条件下开挖面的失稳破坏模式及极限支护力。

假定土体为均质、各向同性的弹塑性材料，且符合摩尔库伦屈服准则。根据Vermeer等[14]的研究结果，弹性模量与泊松比的大小只对荷载位移曲线有影响，但对最终极限支护力的大小没有影响。

数值模拟采用总应力法进行，则地层可以认为是无摩擦性的纯黏性土，即地层黏聚力c取不排水抗剪强度Cu，内摩擦角取0°。分别以隧道埋深比C/D(C为隧道埋深)、隧道直径D、土体黏聚力c、土体重度γ为变量展开数值模拟，当隧道直径D=8 m，c=20 kPa，γ=18 kN/m3时，埋深比为0.5、1、1.5、2、3时，分别记为工况1～工况5；取隧道直径D分别为10 m与12 m时，对应的工况分别为工况6～工况10与工况11～工况15；取隧道直径D=10 m，C/D=2，γ=18 kN/m3，数值模拟计算黏聚力c为15、20、25、30、35 kPa，记为工况16～工况20，具体计算工况及土体参数如表1所示。

表1 模型计算参数Table 1 Calculation parameters

假定水位线始终位于地表，地表超载为零，模型边界达到可以避免受到边界条件的影响，对模型四周及底部施加固定约束，模型上表面的边界自由。计算模型如图1所示。

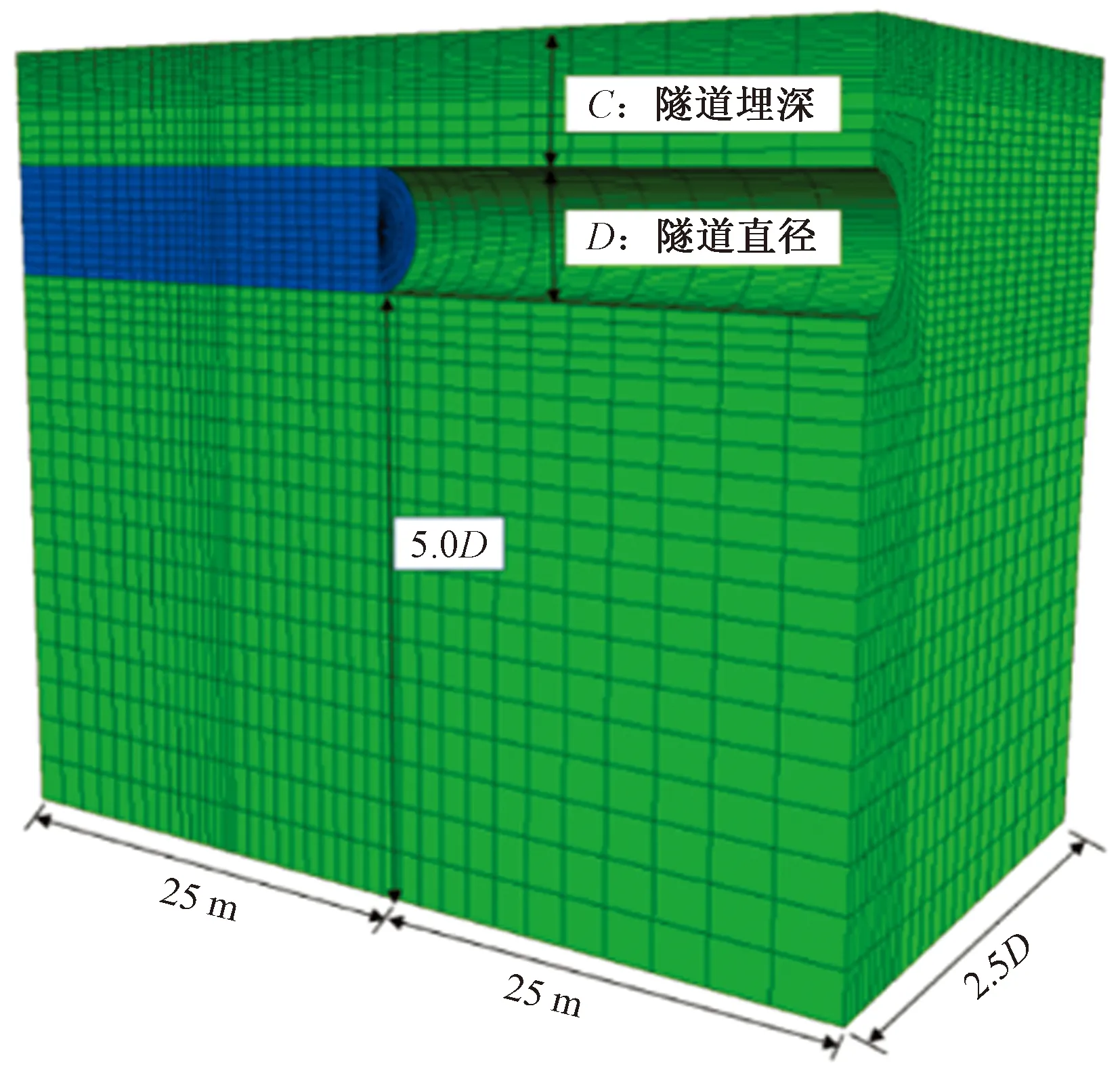
图1 开挖面稳定性数值模型示意图Fig.1 Numerical model for the analysis of tunnel face stability

数值模拟中，原始地层施加在开挖面上的压力实际为梯形分布力，数值模拟中施加在开挖面上的支护力为均布力，其初始大小与开挖面前方的初始静止土压力合力大小相等；采用二分法逐步降低开挖面处支护力的展开模拟计算，当监测点的土体位移无限增大，则认为开挖面前方土体达到塑性流动状态，开挖面发生破坏，以此确定开挖面的极限支护力以及极限状态下开挖面前方的土体松散坍塌破坏范围。

1.2 隧道埋深对开挖面极限支护力的影响

数值模拟得到了隧道埋深对开挖面极限支护力的影响规律，如图2所示。可以看出，随着隧道埋深的增大，开挖面极限支护力不断增大，近似呈线性关系，这一规律与无水地层完全不同[35]。因此，在富水黏土地层中，地下水对隧道开挖面稳定性有着决定性的影响，应予以高度重视。

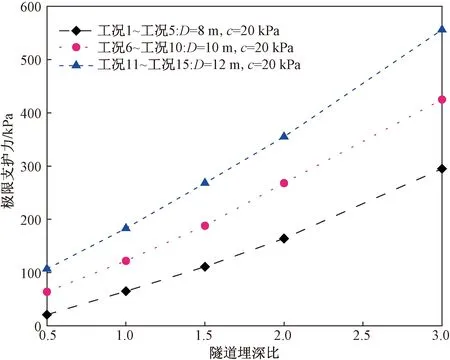
图2 隧道埋深比C/D对极限支护力的影响Fig.2 The influence of C/D on the limit supporting pressure

1.3 隧道直径对开挖面极限支护力的影响

数值模拟得到了隧道直径对开挖面极限支护力的影响影响规律，如图3所示。可以看出，随着隧道直径的增大，开挖面上的极限支护力不断增大，近似呈线性关系。

图3 隧道极限支护力随隧道直径的影响Fig.3 The influence of D on the limit supporting pressure

1.4 土体黏聚力对开挖面极限支护力的影响

数值模拟得到了土体黏聚力对隧道开挖面极限支护力的影响规律，如图4所示。可以看出，随着土体黏聚力的增大，隧道开挖面极限支护力不断降低，近似呈线性关系。这一规律与Zhang等[11]所研究的无水地层和王帆[2]所研究的浅埋富水黏土地层是一致的，即无论是无水地层还是有水地层，无论浅埋还是深埋，土体黏聚力对开挖面极限支护力都有显著的影响，黏聚力越大，大直径盾构所需的支护力越小。

图4 土体黏聚力对隧道极限支护力的影响曲线Fig.4 The influence of c on the limit supporting pressure

1.5 极限状态下开挖面的变形特性

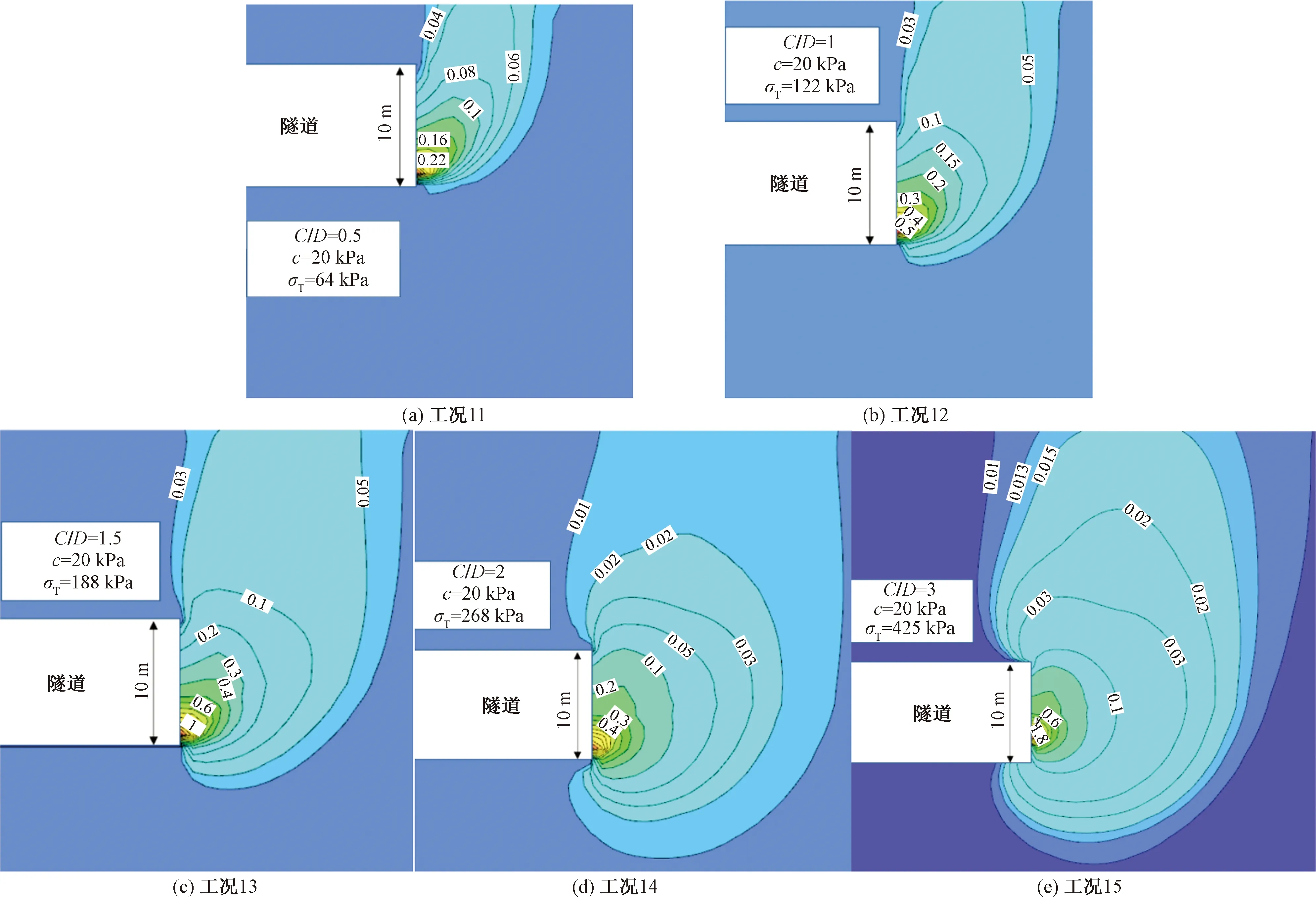
图5 不同C/D下破坏区位移云图Fig.5 Contours of displacement for various C/D

图5给出了5种具有代表性的工况，即工况11～工况15，当隧道直径D=10 m，黏聚力c=20 kPa时，隧道埋深为C/D=0.5～3.0时的极限支护力σT下开挖面前方破坏区土体的位移云图。可以看出，在开挖面前的破坏区范围内，土体位移云图呈波纹状堆叠，向地表发展。当隧道埋深较浅时，破坏区的延伸至地表，而随着埋深的增大，也可以看出开挖面前方破坏区扩散至地表的迹象。分析认为，富水地层盾构隧道与无水砂土地层不同，富水地层在不排水效应分析下，无法形成稳定的拱区，开挖面会逐渐延伸至地表，且相比于无水砂土地层，不排水效应下开挖面的破坏区范围更大。

2 理论解析模型

在不排水条件下的匀质黏性土层中，根据数值模拟分析结果，开挖面的极限支护力随着隧道直径与埋深的线性增大而增大，随着土体黏聚力的线性增大而减小。

现有理论研究中，针对富水地层不排水分析，王帆[2]提出了一种新的计算模型，通过改进由两个刚性截锥体的构成的三维破坏机制所得。当隧道埋深较浅时，利用该破坏模式求得的极限支护力与数值模拟较为接近，与离心试验的破坏形状吻合较好，但当隧道埋深较大时，求得的极限支护力与数值模拟差距逐渐增大，假定破坏区垂直延伸至地表的假设也与实际不符。该计算模型如图6所示。

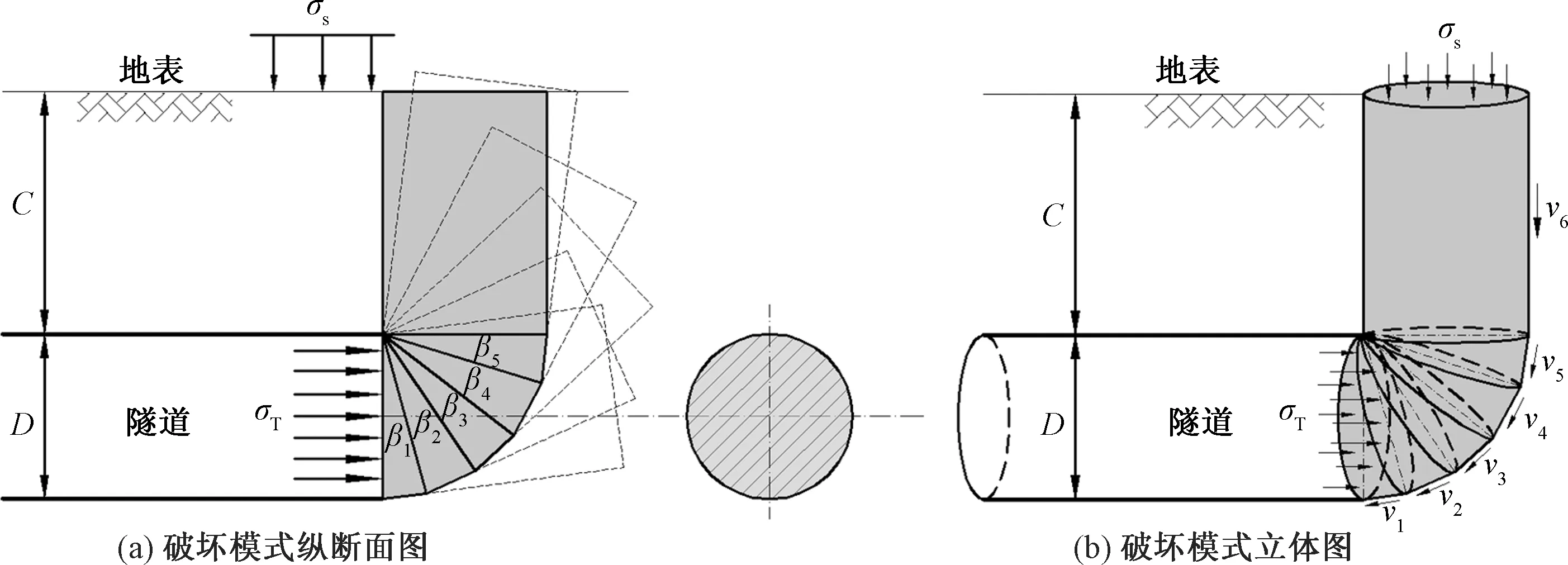
C为隧道埋深; D为隧道直径;σs为地面超载;σT为开挖面处支护力; β1～β6为截锥体之间的夹角;v1～v6为各个块体的速度图6 均质土不排水条件下开挖面稳定性分析模型[2]Fig.6 Analysis model for face stability in homogeneous soil in undrained condition[2]

2.1 截椭圆柱体的破坏区域能量构成分析

如图7所示，截椭圆柱体破坏模式[2]得到的解析解相比于数值模拟得到的解较小，且在埋深较浅时候，两者的差异较小，而随着埋深的进一步增大，两者的差异逐渐增大，最大差异达到19.18%。数值模拟与解析解的差异随埋深的增大而增大，分析认为是由于计算模型的假定不合理导致。王帆[2]给出的开挖面位移云图也可以得到相似的结论，假定的计算模型与数值模拟得到的破坏区存在一定差距，在隧道埋深较深时候尤为明显。

图7 不同C/D情况下解析解与数值解的对比曲线Fig.7 Comparison of analytical solutions with numerical solutions for various C/D conditions

将王帆[2]提出的破坏模式分为两个区域，如图8所示，依据极限分析法中的功率构成，对两区域的虚功率进行分析。

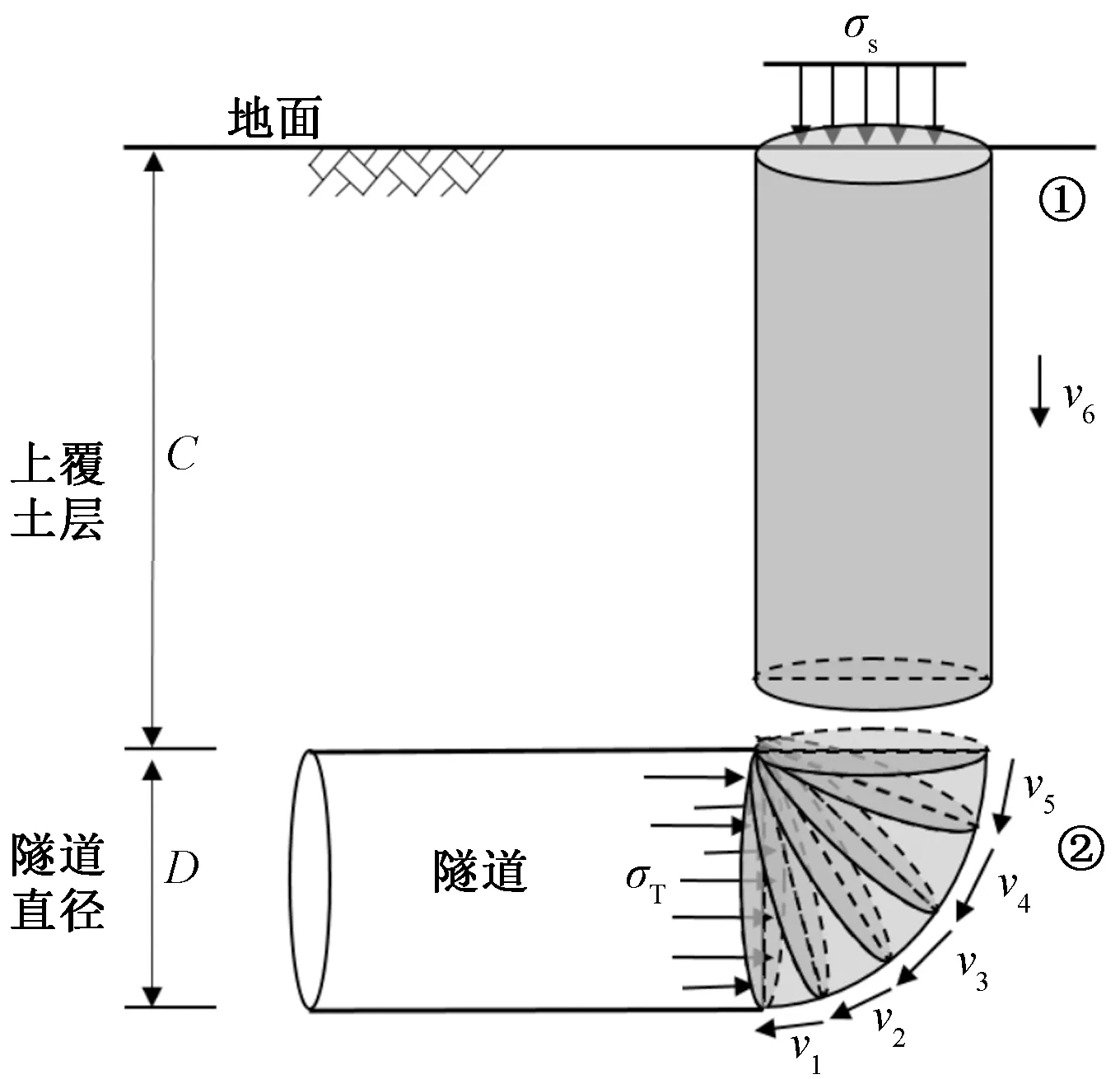
图8 破坏区模型图Fig.8 Model of the failure zone

根据极限分析法上限定理，隧道开挖面保持稳定的条件为

Pe≤Pv

(1)

式(1)中：Pe为外力虚功率；Pv为破坏区范围内部能量耗散率。外力虚功率Pe包括3个部分：开挖面支护力的虚功率PT，地表超载的虚功率PS，破坏区土体重力的虚功率Pγ。

对于每一个具体的工况，都可以通过优化求解出对应的极限支护力，并同时求出多块体破坏机制中的各个角度，各个参数。即可以求得不同工况下的Pe、PT、PS、Pγ。分析不同工况下各个部分的功率构成关系。

Pe=PT+PS+Pγ

(2)

结合图8，将式(2)中Pγ和Pe各分为两部分，分别记为Pγ①、Pγ②和Pe①、Pe②，式(2)可以转化为

-PT-PS=(Pγ①-Pe①)+(Pγ②-Pe②)

(3)

当地面超载不变时，(Pγ①-Pe①)和(Pγ②-Pe②)决定开挖面的极限支护力的大小。假设地表超载为0，各种工况下的两个部分的虚功率占比如表2所示。

表2 虚功率分析计算工况Table 2 The working condition of virtual power analysis calculation

采用极限分析法进行反算，分析两个部分的功率占比情况，计算结果如表3所示，计算中假定速度v1=1，表中数值无量纲，仅表示数值上的相对大小。

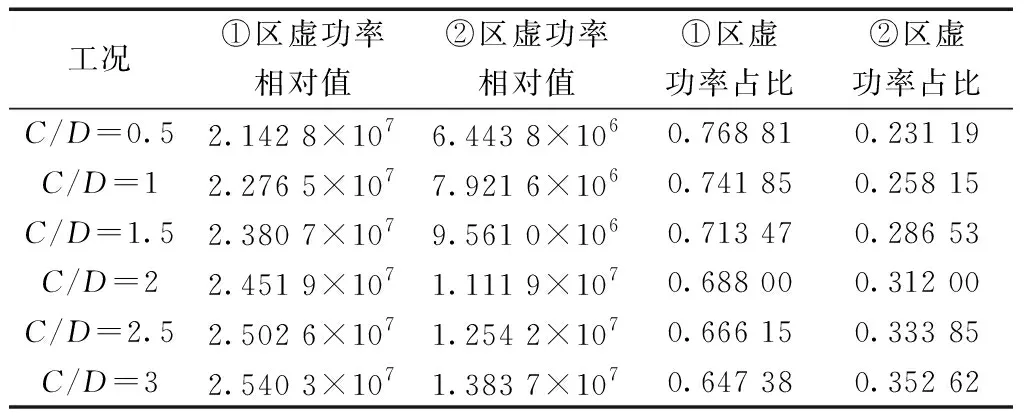
表3 破坏区功率分析Table 3 The virtual power of failure zone

由表3可知，在隧道的埋深从C/D=0.5变化到C/D=3的过程中，破坏区两部分的功率都逐渐增加，即开挖面支护力的功率也逐渐增加。在两部分的功率逐渐增大的过程中，①区功率占比逐渐减小，②区功率占比逐渐增大，表明随着埋深的增大，破坏区①区和②区两部分功率增大导致极限支护力的增大，但①区部分的功率增加的速率远小于②区。

该破坏模式下的极限支护力随着埋深增大时，理论解与数值模拟的差异越来越大，结合功率分析认为，出现这一差异的主要原因是由于破坏区①区的破坏范围假定不合理，导致随埋深增大时，破坏区①区的功率增大速率偏小，从而使得极限支护力的大小与数值模拟偏离较大。

2.2 基于离心试验与功率分析修正极限支护力

不排水黏土地层中的数值模拟中，开挖面的破坏区范围难以根据位移云图划分出合理的形状[2]。根据Schofield[38]在不排水地层的离心试验结果，破坏区的轮廓线如图9所示。

从图9可知，开挖面发生破坏时，开挖面正前方破坏区轮廓线呈较为规则的弧形，出隧道顶部之后，沿着两边斜向延伸至地表，提取离心试验的破坏区边界线。利用开挖面稳定性系数N描述开挖面的稳定状态时，支护力越大，N越小，开挖面越稳定。同时，采用极限分析法求解极限支护力时候，计算得到的极限支护力越大，即稳定系数N越小，就越准确。根据截椭圆柱体模型，利用极限分析法求解出的开挖面稳定系数N、破坏区的几何参数与离心试验结果对比，如图10所示。

图9 不排水黏土地层开挖面主动破坏的离心机试验结果[38]Fig.9 Centrifuge test results of active failure in undrained clays[38]

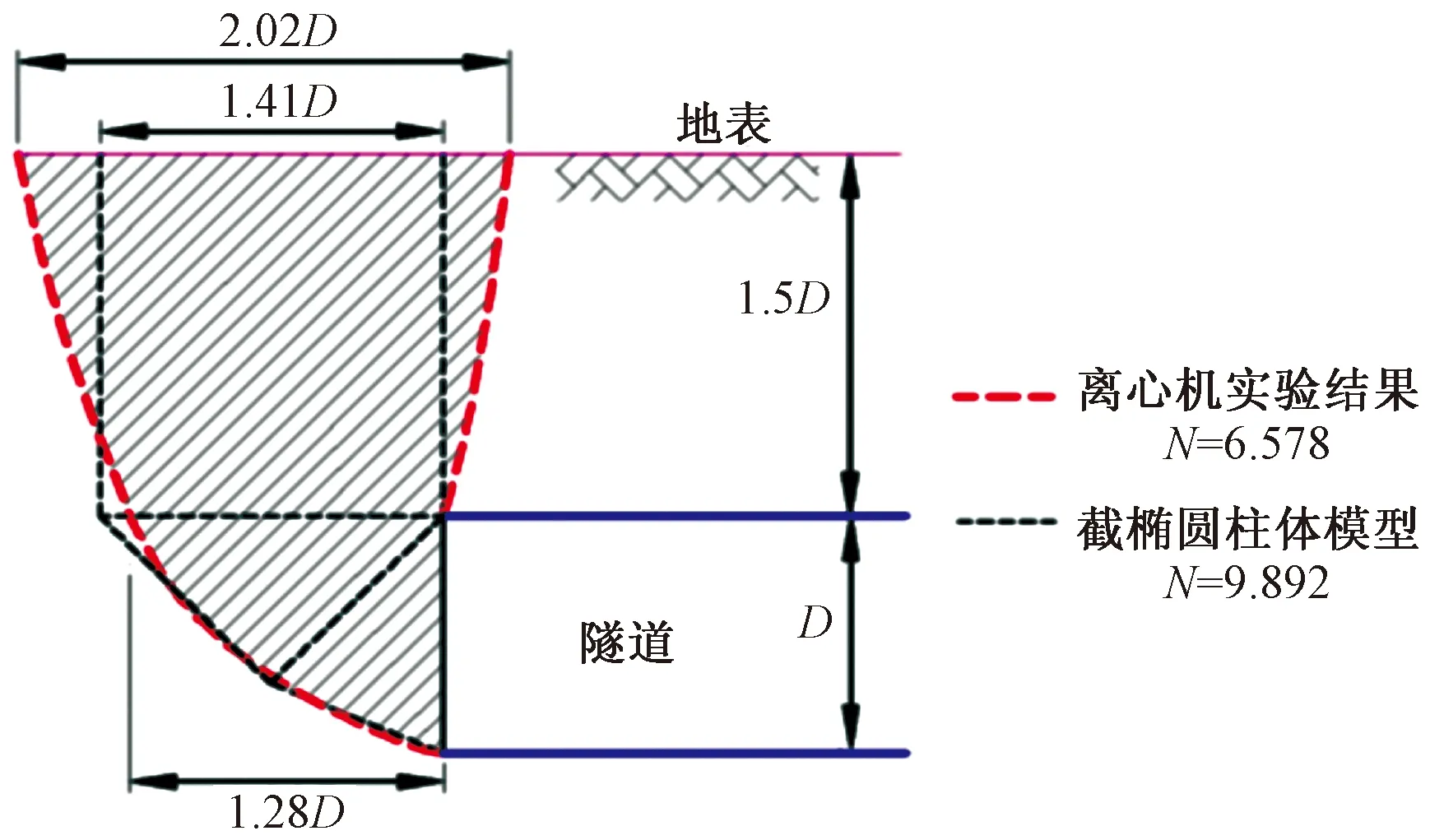
图10 本文解析解与离心机试验结果的破坏区对比Fig.10 Comparison of the failure zone between the proposed model and the centrifuge test

从图10可知，利用截椭圆锥体模型求得的破坏区下部②区与离心试验结果吻合较好，破坏区上部①区与离心试验差距较大；求得稳定系数N相比离心试验较大，即极限支护力较小。分析认为极限支护力较小的原因在于，利用截椭圆柱体模型计算时，上部破坏区①区的范围太小。

不排水黏土地层开挖面发生破坏失稳时，数值模拟和离心试验都难以得出明确规则的破坏形状，难以提炼总结。而通过对破坏区的功率进行分析，认为破坏区上部的不合理使得该区域的虚构率较小，从而使得计算得到的极限支护力偏小。

根据不排水黏土地层开挖面主动破坏的离心机试验结果，对于截圆柱体破坏模式的上部进行修正。根据图5，对比离心试验与破坏区的平面二维形状，给出修正系数，利用修正系数对破坏区①区的功率进行修正，从而修正极限支护力。

例如，如图10所示，当C/D=1.5时，离心试验得到的破坏区①区截面接近一个梯形，理论计算得到破坏区①区截面呈矩形，功率简易修正系数ξ根据梯形两部分面积比率求得，即

(4)

根据表2，可知破坏区①区的功率占比为0.713，②区占比为0.287，利用修正系数ξ进行修正后，开挖面极限支护力的修正系数为k为

k=0.713×1.17+0.287=1.121

(5)

此时，在表2中，工况3：C/D=1.5，D=10 m,c=20 kPa，φ=0°，γ=18 kN/m3，修正后的极限支护力为162.17×1.121=181.8 kPa。

3 理论解析模型与数值模拟结果的对比分析

破坏区①区功率简易修正系数ξ是结合Schofield的离心试验结果求得，离心试验给出工况并不完全。因而，结合埋深将修正系数假定两种情况。

(1)ξ为定值，与埋深无关时，即ξ=1.17，则随C/D变化时，结合各部分功率占比，开挖面极限支护力的修正系数k如表4所示。

表4 修正系数ξTable 4 Correction coefficient ξ

(2)ξ不为定值，与埋深有关时，假定开挖面破坏区①区两边的张开角度相同，且破坏区界面为底边固定1.41D的梯形，则结合各部分功率占比，开挖面极限支护力的修正系数k如表5所示。

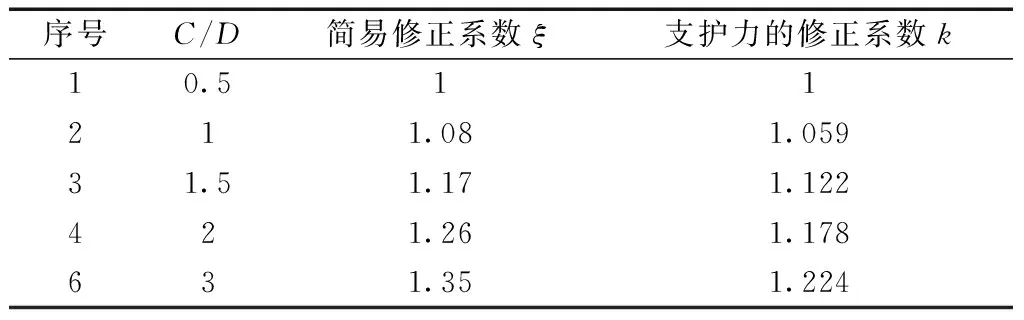
表5 修正系数 ξTable 5 Correction coefficient ξ

3.1 修正极限支护力与数值模拟对比分析

为了验证截椭圆锥体[2]破坏模式在经过修正系数ξ修正后得到的极限支护力的正确性，将截椭圆锥体破坏模式修正系数ξ为定值时以及ξ随埋深变化时等理论计算得到的极限支护力，与FLAC3D数值模拟得到的极限支护力数值解进行对比。

设置参数如下：隧道直径D=10 m，土体内摩擦角φ=0°，内黏聚力c=20 kPa，埋深C/D分别为0.5、1、1.5、2、3。解析解和数值解的计算结果如表6所示，解析解和数值解随埋深比C/D的变化曲线如图11所示。

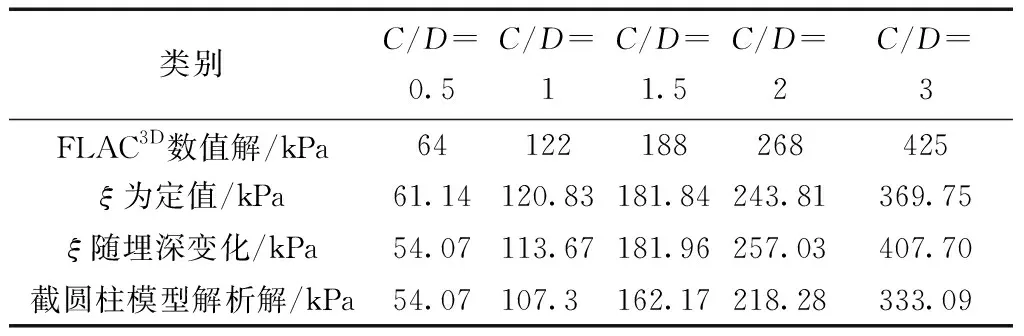
表6 解析解与数值解的差异对比

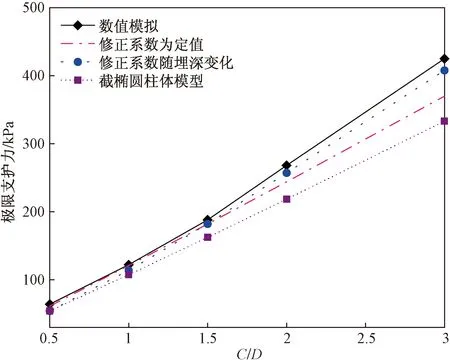
图11 不同C/D情况下解析解与数值解的对比曲线Fig.11 Comparison of analytical solutions with numerical solutions for various C/D

从表6和图11可以看出所有解析解与数值解均随埋深比的增大而增大；相较于数值解，所有解析解求出的极限支护力解偏小；3组解析解中，截椭圆椎体模型得到极限支护力与数值模拟相差最远；当埋深比C/D<1.5时，ξ为定值时更加接近数值模拟，当埋深比C/D>1.5，ξ随埋深变化时得到的极限支护力更加吻合数值解。

3.2 与离心试验结果以及已有模型解析解的对比

在不排水均质黏土地层的隧道中，Broms等[39]提出开挖面稳定性系数计算公式为

N=[σs-σT+γ(C+D/2)]/cu

(6)

式(6)中：cu为土体的不排水剪切强度。

式(6)用以描述开挖面的稳定程度，该稳定系数后来被许多学者用来研究开挖面的稳定性。

计算参数采用隧道直径D=10 m，埋深比C/D=1.5，土体内摩擦角φ=0°，内黏聚力c=20 kPa。图12给出了修正后的极限支护力(ξ固定与变化时)下对应的隧道开挖面稳定系数N，并与已有不排水条件下隧道开挖面稳定系数的研究成果[2，40-41]数值模拟计算结果进行对比。可以看出：在C/D=1.5时，利用修正系数ξ(不固定)修正的极限支护力比Davis等[40]的上限解改善了13%，相比Mollon等[41]的解改善了10%，相比王帆[2]的解改善了2%，更加接近数值模拟结果。对比结果表明利用修正系数ξ对极限支护力进行修正的有效性。

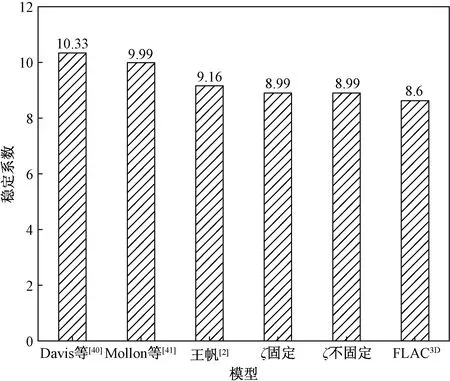
图12 C/D=1.5时所得解析解与已有解稳定系数的对比Fig.12 Comparison of stability coefficient ratios between analytical solution and existing solution for C/D=1.5

4 工程应用与分析

常州轨道交通2号线青洋路站—丁塘河公园站盾构区间上下行线全长1 878.121 m。青洋路—丁塘河公园站区间地面标高一般在4.20～4.70 m,轨面埋深为15.6～25.8 m，隧道拱顶埋深为10.6～20.8 m。

该线路段作为该工程重点控制的风险源之一，采取了以下措施。

(1)采用土压平衡盾构施工，严格控制掘进速度及出土量，匀速缓慢掘进。

(2)下穿施工前施作试验段，并根据试验结果优化盾构参数。

(3)加强同步注浆及二次注浆，砂层注浆系数为2.0，黏土层为1.8。

(4)加强监控量测，并做好应急预案。

在隧道施工时，开挖面稳定性的控制显得尤为重要，施工中需要格外注意盾构的施工参数，以保证开挖面的稳定。

地层参数如表7所示。本区间穿越的地层为：⑥1粉质黏土、⑥2粉质黏土、⑥3黏土、⑥4粉质黏土等。

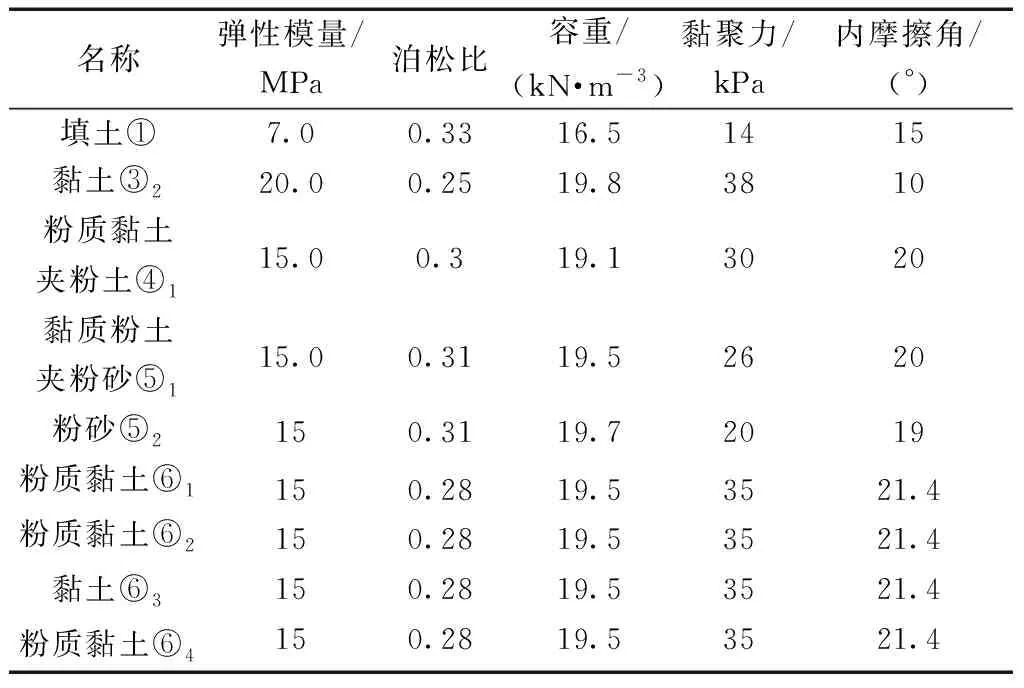
表7 土体计算参数Table 7 Calculation parameters of soil

隧道处于低渗透性的黏土地层中，开挖掘进速度较快，则地下水来不及发生渗流，超孔隙水压力来不及消散，视为不排水效应。根据不排水效应进行分析，内摩擦角为0°，黏聚力取隧道所在地层黏聚力，利用极限支护力修正方法求解极限支护力，并与数值模拟进行对比分析。隧道上方覆土根据质量等效简化为均一地层的重度，具体的参数如表8所示。

表8 计算参数Table 8 Calculation parameters

根据表8给出的土体计算参数，采用现有针对不排水地层的理论计算开挖面极限支护力，并利用修正系数对极限支护力进行修正，然后与数值模拟等进行对比。对比结果如图13所示。可以看出，修正后的极限支护力与文献给出的截椭圆柱模型相比，修正后的极限支护力更加接近数值模拟结果，且当修正系数随埋深变化时得到的极限支护力较大且更接近数值模拟结果。

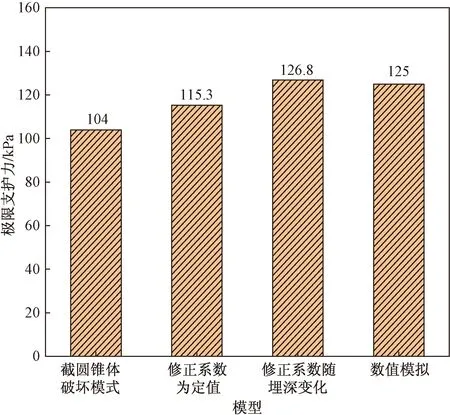
图13 开挖面稳定性研究在常州地铁工程上的应用Fig.13 The application of the research of the face stability of tunnel face to asubway project in Changzhou

5 结论

针对富水黏土地层盾构隧道，对不排水条件下的开挖面稳定性展开了研究，具体包括数值模拟和理论分析。通过数值模拟研究，分析各种参数对极限支护力的影响规律；推导已有的适用于不排水分析的开挖面主动破坏模式，分析其功率构成，结合黏土不排水离心试验得到破坏区域范围，对极限分析法获得的极限支护力进行修正。最后通过对比前人研究、数值模拟等验证了极限支护力修正的正确性。获得的主要结论如下。

(1)展开富水地层不排水情况下的数值模拟，不排水盾构隧道中，当黏聚力c=0 kPa，极限支护力与隧道直径、隧道埋深成正比，与土体黏聚力成反比。

(2)针对匀质富水地层盾构隧道，将既有破坏模式分成两个区域，展开功率分析。通过分析认为：截椭圆柱体破坏模式的解与数值模拟偏差越来越大的主要原因是破坏模式的上部的假定不合理。

(3)结合离心试验，对离心试验的破坏区域范围与截椭圆柱破坏模式求得的开挖面稳定系数N、破坏范围进行对比。进一步确定了截椭圆柱破坏模式上部的不合理。基于离心试验，提出极限支护力修正系数ξ。

(4)假设隧道埋深逐渐增加，将修正后的极限支护力、数值模拟、截椭圆主体破坏模式求得的极限支护力进行对比。认为修正后的极限支护力与数值模拟结果更加吻合，且当修正系数ξ随埋深变化时，随着C/D的增加，与数值模拟吻合最好。

(5)对比王帆[2]、Davis等[40]、Mollon等[41]以及数值模拟得到的稳定系数N，验证了修正极限支护力方法的合理性。