假塑性流体模型在橡胶冷流道注射硫化机模具改造设计中的应用

尤兆鑫，徐春美

(泰克国际（上海）技术橡胶有限公司 ，上海 松江区 201600)

冷流道注射方式作为一种比较先进生产方式，较之热流道工艺具有以下的好处[1]：

（1）流道内压力损失小，温度均匀，胶料流动性越好，产品的内应力、变形就会越小，产品的力学性能和表面质量就会越高（常见的飞边、缩水、熔接痕、颜色不均、填充不足等现象就可以减少）。

（2）大部分或全部流道内的废料被消除，提高了物料的有效利用率，减少了旧料的回收利用。

（3）缩短了成型周期和开模行程，提高了生产效率。

（4）冷流道可以自动切断浇口与制品的连接，自动化程度得到了提高。

（5）降低注射压力，有利于保护模具，延长使用寿命。

（6）可保证多模腔模具填充均匀，质量一致。

所以将现有的热流道模具改造为冷流道模具是非常必要的，由于和热流道模具的设计不一样，冷流道的模具的流道是封闭式的，在改造过程中是否可以进一步扩充生产区域和单模硫化的生产量，从而提高生产效率，是本文重点探讨的问题。

1 改造内容

1.1 改造介绍

1.1.1 产品

轮胎修补用 Φ30×4.0蘑菇钉 （头部直径30 mm；塞梗直径4 mm）

1.1.2 生产设备

品牌 “磐石” GVT5-100注射式硫化机， 有效加热面积：430 mm×600 mm

1.1.3 改造内容

（1）热流道模具 改造为 冷流道模具。

（2）64孔射出 改造为 80孔射出。

1.2 改造研讨

本文1.1.3改造内容 （1）不在本文讨论范围内，重点对改造内容（2）进行研讨。

1.2.1 原模具简述

原冷流道模具采用的是等距式流道64孔结构，其流道方向如图1， 依次为（括号内为数量） ：注射口（1）→1级流道（2）→2级流道（4）→3级流道（8）→4级流道（16）→5级流道（64）。

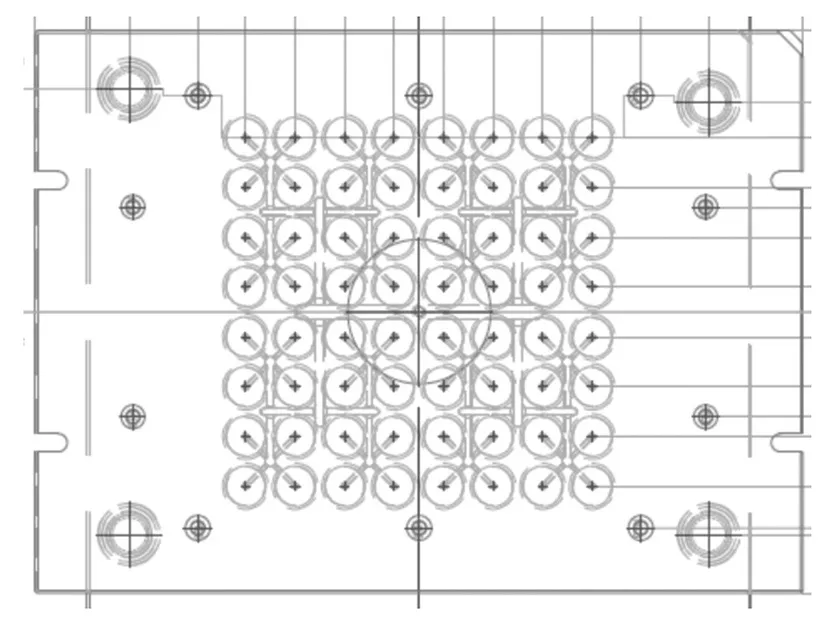
图1 等距式流道64孔分布示意图A

其中 1级流道～5级流道均为热流道。

这种结构有以下特点：

（1）流道截距按照等级减少。

（2）到达每一个型腔的路径一致，折点数一致，每一个分支拐点以后的路径相顾始终处于轴对称状态，如图2中随机选取的红线和蓝线所示：

图2 等距式流道64孔分布示意图B

1.2.2 增孔后模具

从上面可以看到，整个模具板上在左右两侧各有一片空白区域没有得到利用，烤炉在此处增设两组各8各型腔，使模具的型腔数量从原来的64孔增加至80孔，单模硫化效率提高25%，如图3所示：

图3 80孔分布示意图

从上图可以看到在原模具的左右两侧各增加了两组共16个型腔，其流道方向为：

注射口（1）→1级流道（2）

→2级流道（4）→3级流道（8）→4级流道（16）→5级流道（64）；

→3级流道（2）→4级流道（4）→5级流道（8）。

其中，1级流道～3级流道为冷流道，4级流道～5级流道为热流道。

1.2.3 新模具问题描述

可以看到，一般来说，冷流道的设计是需要把橡胶均匀的注入模具型腔，通常为均匀堆成分布，如图4。

图4 流道修改示意

增加了孔位的新模具（图4右）打破了原来（图4左）同长度，同拐点，对称路径的设计方法，在两端有一个直接从1级流道过渡到3级流道的设计，且少了一个拐点。因此，需要计算新流道的分配情况，并通过一定的通道设计，保证10个注胶口的流动基本均匀。那么这种设计，会不会导致各个型腔的橡胶压力分布不均，从而产生缺胶等不良或者在非制品位置产生溢胶，是模具制作前需要验证的问题。

2 假塑性流体模型验证计算

为了防止模具制作完成后产品出现不良等非期待行结果，决定对设计完成的模具流道建立假塑性流体模型进行验证，计算各个注射口的流量分配情况。

2.1 工况说明

根据硫化机特性，注射机每次的注射量约为300～400 mL，时间9～20 s，此处取平均情况，即15 s内完成350 mL的注射量，且假设橡胶流体特性如下：

（1）流体为不可压缩流体。

（2）流体的流动为等温稳态流动，即在冷流道过程中不存在明显的热交换，且流道内可以完全充满橡胶，即不存在气体+胶体的两相混合情况。

（3）流道内流动按层流考虑。

2.2 计算依据

本计算书中的仿真案例包括基本的非牛顿流体流动问题。采用商业计算软件完成，在计算流体力学的基本原理中，流动可以用以下方程描述：

（1）连续性方程（质量守恒方程）

该定律可表述为：单位时间内流体微元体重质量的增加，等于同一时间间隔内流入该微元体的净重量，其表达式如下：

（2）动量守恒方程（N-S方程）

该定律可表述为：微元体中流体的动量对时间的变化率等于外界作用在该微元体上的各种力之和，x,y,z三个方向上的表达式如下：

（3）能量方程

该定律可表述为：微元体中能量的增加率等于进入微元体的净热流量加上体力与面力对微元体所做的功，实际上即热力学第一定律，其表达式如下：

（4）本构方程

橡胶的流动符合假塑性流体特征，即流体黏度随剪切速率存在如图5所示的变化, 在剪切应力较小时，流动表现出牛顿流体的性质，此时为零剪切黏度；随着剪切应力增加，黏度出现急剧变化，此时即为假塑性区；当剪切应力继续增加，黏度再次表现为牛顿流体性质，此时为极限剪切黏度。

图5 假塑性流体黏度特征

在计算时，采用合理的本构模型来进行描述，此处选用简化的三参量Cross模型，其表达式如下：

式中， 为所求的当前状态黏度。 为零剪切黏度，为剪切速率， 为松弛时间。 为非牛顿指数。对于该工况中的橡胶制品，选取各参数如表1[2]：

表1 橡胶制品牛顿指数表

2.3 计算模型说明

选取计算模型如图6所示，上方为注射口，下方对应10个出口，其中两端新加的出口管路上，通过一定的缩径设计，来控制阻力和流量。

图6 计算模型示意

对计算区域绘制网格如图7：

图7 网格划分示意

网格参数及扭曲度指标如图8所示，最大扭曲度处于0.9之内，满足计算需求。

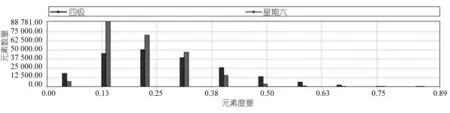
图8 网格扭曲度示意

对不同区域，设置方法列表如图9（入口），图10（出口）。

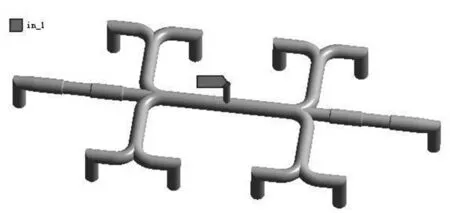
图9 入口边界位置示意

图10 入口边界位置示意

2.4 仿真结果

采用如上设置进行仿真计算，计算残差曲线如图11所示，可以认为计算收敛。

图11 流体方程收敛曲线

选取截面速度场分布如图12。

图12 截面速度场云图

选取截面压力场分布如图13。

图13 截面压力场云图

读取各出口的流量分布情况如下表2所示。

从表2结果看：

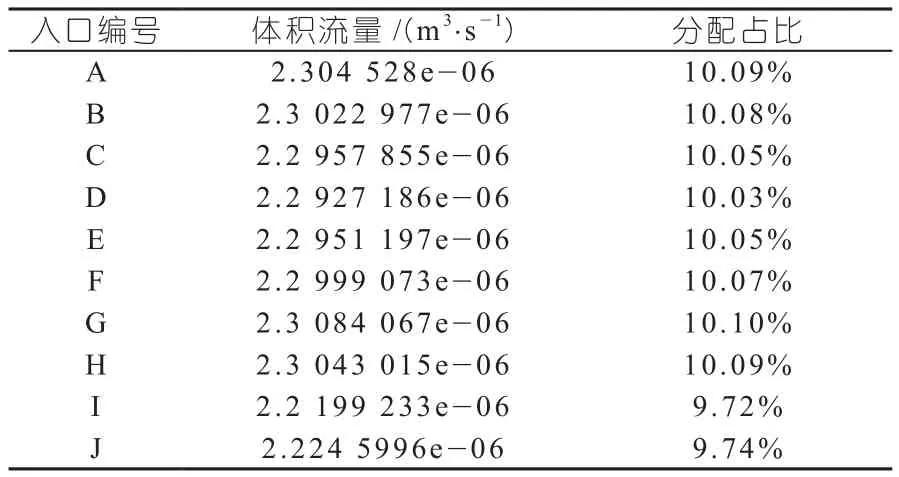
表2 各区域分配占比

（1）新增的I～J口的设计流量占比要小于A～H口；

（2）A～H口的分布均匀，流量分配较I～J口高2.5%左右。

按照经验判断，2.5%在可以接受范围之内，不会对产品和生产造成影响。

3 生产结果

按照验证后的结果，改造完成的冷流道模具生产顺畅，没有出现因胶料分配不均导致的缺胶以及非制品区的溢胶等不良现象，如下图14。

图14 完成品照片

本次改造成功。