长岭县降水量变化特征分析

陈 实，孙颖娜，萨日娜，张丽娜

（黑龙江大学水利电力学院,黑龙江 哈尔滨 150080）

降水的时空变化规律在开展水利工程开发建设、防汛排涝抗旱、水资源的合理开发利用等工作中具有重大意义,对于水库调度管理、气候变化影响评估、工农业生产、水土保持规划设计、水资源和水电工程,对国民经济的可持续发展也具有极其重要的影响。细致地研究一个地区的降雨周期,对当地的防洪抗涝、水文预报、人民的生产生活具有深远意义。

安宝军在研究沱沱河流域时,应用滑动平均法,累积距平法进行研究分析,细致地研究了这两个流域的降水变化趋势与特征[1]。赵双庆等通过小波分析法和M-K 秩次相关法,对董志塬1959年～2016年的实测降水资料进行趋势分析,得出了董志塬区年降水量变化呈逐年不显著上升的结果[2]。M-k检验法是被世界气象组织推荐的一种检验方法,因为其计算较为简便,不需要服从或属于某种分布,个别异常值对检验几乎没有影响,因此被广泛使用。易云凤运用数理统计方法,对宣汉的逐日降水数据进行整理,对宣汉的暴雨频次进行了细致分析,为宣汉当地的生产生活,降低强降水引发的地质灾害造成的经济损失做出了极大贡献[3]。通过上述研究可以看出,降水在不同的时空区域上存在明显差异,根据长岭县1967年～2018年逐月降水资料,运用滑动平均法及M-K 秩次检验法,分析长岭县内降水变化特征。

1 研究区概况

长岭县地处于吉林省西部地区,东临松原市并相互接壤,所以一直以来长岭县都由松原代为管理。长岭县年均气温为4.9℃,具有温带季风大陆性气候性质的自然气候,一年四季季节分带明显,温度季节性变化较大,古人曾有春迟秋早,夏短东长的评价。从资料上得出,降雨、蒸发和人工开采为主要因素,影响着县区内地下水含量及其动态变化。其中,主要补给来源是大气降水。本文对长岭县大气降水进行分析,揭示长岭县降水的变化特性。

2 研究方法

2.1 线性趋势法

利用一元线性回归,对样本中各变量的回归系数进行计算,建立变量和时间之间的回归模型[4]。

设样本量为n,气候变量为x,时间变量为t,建立x 与t 之间的的方程关系如下；

式中：a、b 分别是回归常数与系数。

计算a、b 的方法如下（2）,式（3）所示：

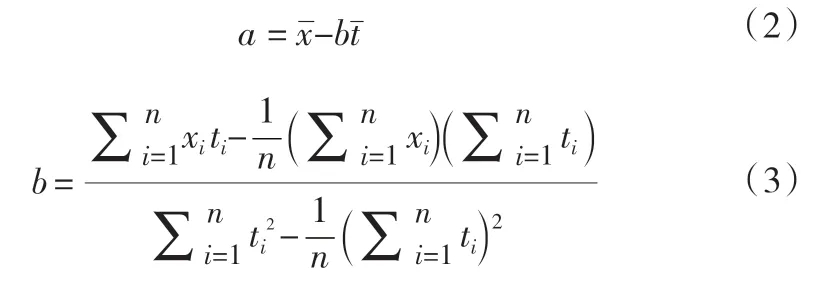
其中,b 为趋势分析系数。

2.2 滑动平均法

通过平均数法简单的计算,对序列的移动平均值进行求算,这样在探求事物发展趋势时,可以消除偶然因素,并据此进行预测[5]。

选取序列资料的x1,x2…,xi每个变量相应的几个前期值,和相同数目的几个后期值,求和取平均值,计算新序列yi,公式为；

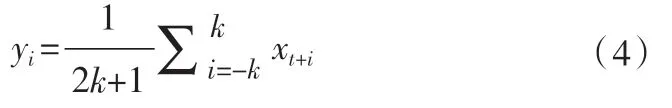
2.3 Mann-kendall 秩次检验法

2.3.1 M-K 趋势检验

（1）根据变量关于时间的序列（x1,x2…,xn）,其中在给定的时间中,各个变量都是独立的。统计变量S 计算公式为；

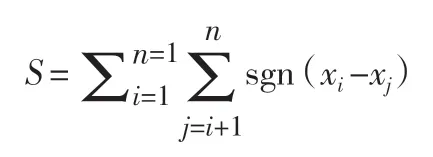
（2）S 的方差计算如下（当时间序列10 时,采用正态近似。）；

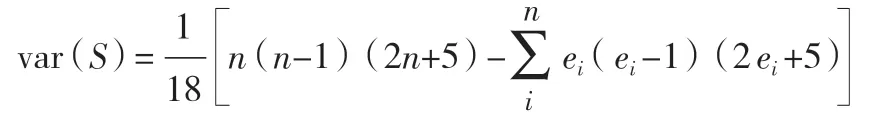
i 为变量中相同样本个数,i 值相同的样本中变量不同的样本个数记为ei。

（3）标准正态分布变量Z 计算如下式；

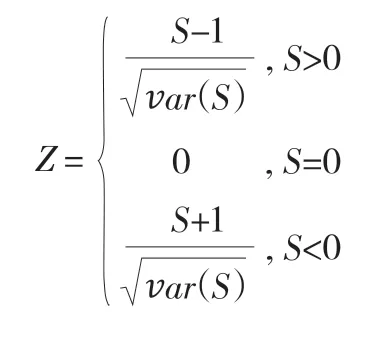
（4）若Z＞z1-a/2,则序列有明显的趋势,当Z 为正,序列趋势上升,若Z 为负,序列趋势下降,用β来表示其具体的变化趋势大小,计算公式如下：

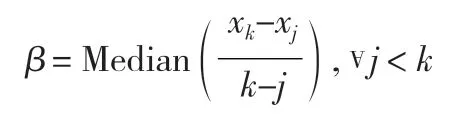
2.3.2 M-K 突变检验法

（1）根据长岭县年降水的时间序列（x1,x2…,xn）,构造一秩序列ri,定义Sk,ri如下；

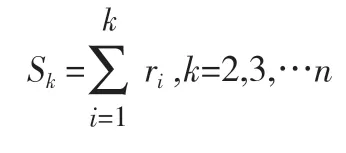
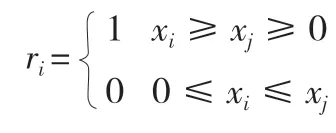
（2）Sk的均值E（sk）与方差Var（sk）的定义公式如下；

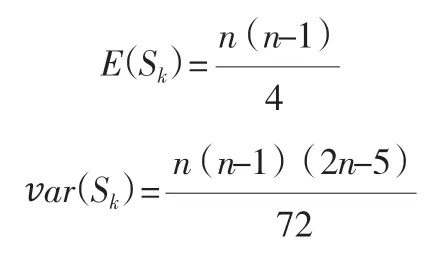
（3）定义统计量UFk；

（4）根据上述过程,时间序列进行逆序列排序,得出新的UFk,令UBk=-UFk,（k=n,n-1,…）,UB1=0。UFk的大小决定序列的趋势走向,当UFk大于0 时,说明序列趋势是上升的,当UFk小于0 时,说明序列趋势是下降的；在给定的置信区间内,如果UFk和UBk的曲线存在交点,那么交点所对应的时间,就是变量发生突变发生的时间[8]。

3 结果与分析

3.1年降水量变化特征分析

根据资料查找的长岭县1967年～2018年的月降水数据,利用上述方法,对长岭县的年降水量进行变化特征分析。

3.1.1 趋势分析和五年滑动平均法分析

在计算及检验统计变化规律中,由于存在波动性的变化,使结果不精确,故运用5 a 滑动平均法,对数据进行处理,使曲线更平滑,消除偶然误差。结果见图1。由图可知；长岭县年平均降水量为433.86 mm,其中,最大降水量为716.2 mm（1983年）,比平均值偏多65%,最小降水量为201.9 mm（2001年）,偏少47%,最大降水量较之最小降水量,多出3.55%,降水变化在近50年间表现出变化幅度很大的特点；5 a 平均降水量最大为532.34 mm（1994年～1998年）,5 a 平均降水量最小为336.84 mm（2006年～2010年）；由趋势分析法和5 a 滑动平均法进行分析的结果可以看出,长岭县年降水量整体上呈下降趋势,但不明显,大体上呈现波动状态。

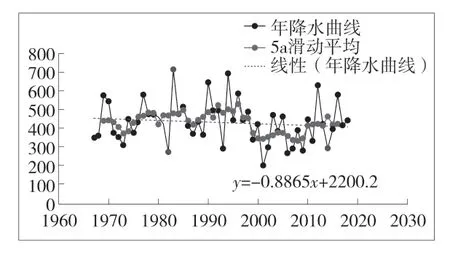
图1 年降水变化趋势

3.1.2 M-K 趋势检验分析

长岭县的年降水量M-K 趋势检验统计参数如下表（2）,从表中可以看出,年降水量趋势分析中位数β=-0.89,表明降水量呈下降趋势,与上面运用趋势分析法得出的结果相吻合,下降幅度为8.9 mm/10 a,M-K 分析检验值Z=-0.86＜1.96,在置信度95%的显著性水平下,表现出不显著下降。

3.1.3 M-K 突变检验分析

表1 长岭县年降雨M-K 趋势检验统计参数

根据上述方法,在0.05 的显著性水平下,对长岭县的年降水量进行突变检验,绘出UFk和UBk的曲线图如图（2）。根据长UFk曲线,判断长岭县近50年的年降水变化趋势；20世纪60年代末期上升,60年代末到70年代初呈显著下降趋势,70年代初到90年代末呈上升趋势,90年代末至今整体呈下降趋势。根据曲线的交点,判断出年降水量在1998年发生突变现象。

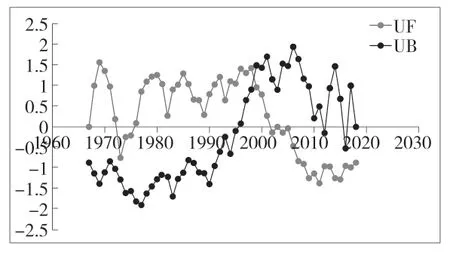
图2 年降水量M-K 突变分析

3.2 季节降水变化特征分析

根据长岭县的自然气候特征,春夏秋冬分别为；3月～5月、6月～8月、9月～11月,12月～次年2月。

3.2.1 运用趋势线法和五年滑动平均法

通过两种方法,对长岭县多年平均季节降水量进行分析,得到的趋势变化过程见图3～图6。根据分析得出；①长岭县降水年内分配不均匀,夏季降水量最多,降水量高达全年总降水的66.69%；春季和秋季相对较少；降水量最少的是冬季,仅占全年总降水的3%。②由趋势分析法得出的趋势线可以看出,长岭县春季降水整体上呈上升趋势,夏季降水整体上呈下降趋势,秋季降水整体上呈下降趋势,冬季降水整体上呈上升趋势。③ 从5 a 滑动曲线上来看；季平均最大降水量为386.24 mm,出现在1993年～1998年的夏季,季平均最小降水量为3.4 mm,出现在1983年～1987 的冬季。

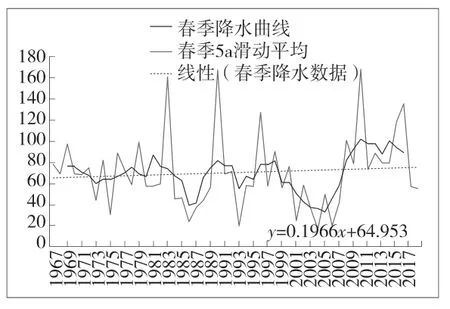
图3 春季降水变化趋势

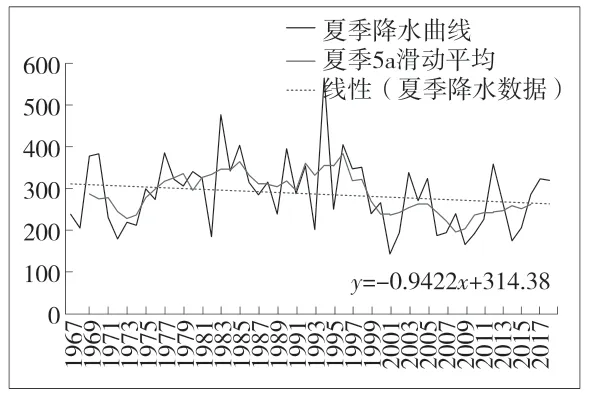
图4 夏季降水变化趋势

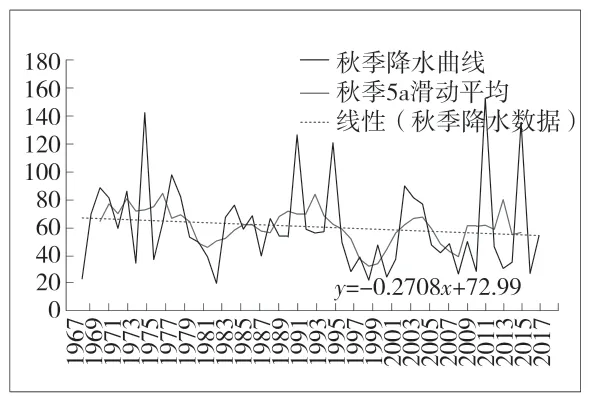
图5 秋季降水变化趋势

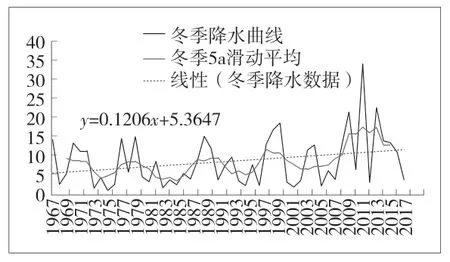
图6 冬季降水变化趋势

3.2.2 M-K 趋势检验分析；

通过前述M-K 趋势检验方法,长岭县近五十年四季降水量M-K 趋势检验统计参数如表2。从表中可以看出,四季的Z 值分别为0.016、-1.097、-1.949、1.468,β值分别为0.004,-0.972,-0.566,0.061,由Z 值和β值可以看出,长岭春冬两季降水呈不显著上升趋夏秋两季降水量呈下降趋势,其中夏季下降趋势显著。

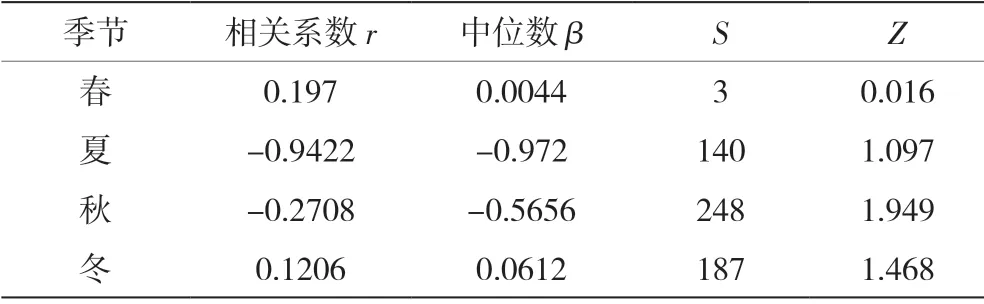
表2 长岭县年降雨M-K 趋势检验统计参数

3.2.3 M-K 突变检验法；

根据上述M-K 突变检验方法,对长岭县四季降水量进行突变分析,其分析结果见图7～图10。

从图7中可以看出,春季UF-UB 在置信区间内存在4 个交点,分别为1969年、1971年、2013年以及2018年,说明长岭县春季降水在这四个时间点发生突变,春季降水量趋势表现为20世纪60年代末至2015年整体呈下降趋势,在20世纪70年代初期短暂上升,2015年至呈现上升趋势,但很不明显。从图8中可以看出,夏季UF-UB 曲线在置信区间内存在3 个点,分别为2001年、2002年、2004年,说明长岭县夏季降水在这三个时间点发生突变,夏季降水在20世纪70年代初-70 末代中呈下降趋势,20世纪70年代末至2007年呈上升趋势,2007年至今呈下降趋势。从图9中可以看出,秋季UF-UB 曲线在置信区间内存在1 个交点,为1993年,即秋季降水在1993年发生突变,从UF 曲线上来看,秋季降水在20世纪70年代初至80年代初呈上升趋势,80年代初至今呈下降趋势。从图10中可以看出,冬季UF-UB 曲线在置信区间内存在一个交点,为2007年,即冬季降水在2007年发生突变,从UF 曲线上来看,冬季降水在60年代末至2008年呈下降趋势,2008年至今呈上升趋势。

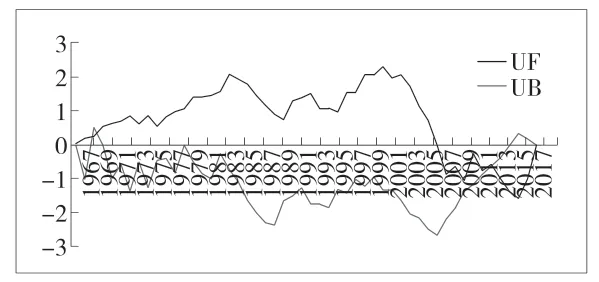
图7 春季降水M-K 突变分析

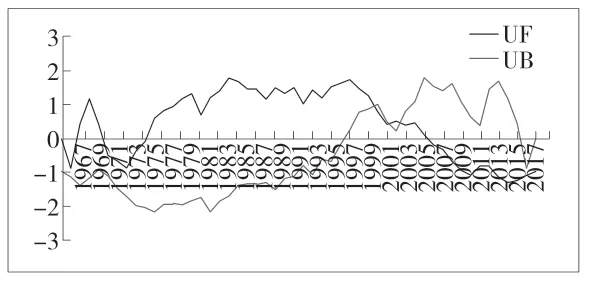
图8 夏季降水M-K 突变分析

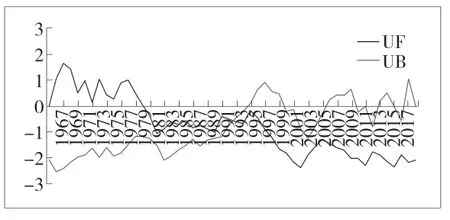
图9 秋季降水M-K 突变分析

图10 冬季降水M-K 突变分析

4 结论

本文以长岭县1967年～2018年逐月降水资料为基础,采用了趋势分析,滑动平均,M-K 秩次检验法。应用Excel、Matlab 等软件,对长岭县的年际、年内降水量进行具体的趋势分析,得出以下结论：

（1）长岭县年降水呈下降趋势,但趋势不显著。

（2）年降水量存在突变性,根据UF-UB 曲线在置信区间内的交点,长岭县年降水量在1998年发生突变。

（3）长岭县春冬天两季降水呈不显著上升趋势,夏秋两季降水呈显著下降趋势,降水主要集中在夏季,其次为秋季与春季,冬季最少。

（4）长岭县四季降水量均存在突变性,根据UF-UB 曲线在置信区间内的交点,长岭县春季降水在研究时间内存在4个突变点,为1969年、1971年、2013年、2018年；夏季降水存在3 个突变点,为2001年、2002年、2004年；秋季降水存在1 个突变点,为1993年；冬季降水存在1 个突变点,为2007年。