超高性能混凝土梁抗弯承载力机理与简化计算

陈俊生，高强，徐承凯

（1.华南理工大学 土木与交通学院，亚热带建筑科学国家重点实验室，广东 广州 510640；2.华南岩土工程研究院，广东 广州 510640）

0 引言

超高性能混凝土（UHPC）是一种新型的纤维增强混凝土材料，不仅克服了传统混凝土抗拉性能不足的缺点，而且在抗压性能、弹性模量和耐久性能等方面都有明显的提高，同时具有较好的流动性[1-4]。

针对UHPC梁的抗弯性能，国内外都展开了一系列的研究[5-8]。Yang等[9]进行了14根UHPC梁的抗弯试验，结果表明，即使截面尺寸和配筋率相同，UHPC的浇筑方法也会影响构件的抗弯承载力。从梁端浇筑UHPC比在跨中浇筑能提供更好的结构性能，说明钢纤维的排列形式和方向受UHPC浇筑方式的影响。付强等[10]分析了不同纵筋配筋率对UHPC梁荷载-挠度曲线的影响，结果表明，梁受压区纵筋配筋率的增加，能够有效约束裂缝的发展，降低梁在加载阶段的挠度。危春根等[11]对3根不同配筋形式的UHPC梁进行了受弯性能试验，结果表明，在相同配筋率下，钢板配筋方案比普通钢筋配筋方案更有利于限制裂缝扩展，但对初裂荷载影响较小。王兆宁[12]进行了3根UHPC配筋梁的抗弯性能试验，在试验基础上建立有限元模型，提出了UHPC配筋梁的开裂荷载以及正截面承载力的计算方法。

目前，针对UHPC梁抗弯性能的研究主要是基于配筋梁进行，而素UHPC梁没有配置钢筋，能够更直接地反映出材料本身的抗弯性能，对比普通钢筋混凝土梁的承载效果，更能推进UHPC构件在实际工程中的应用，但对于素UHPC梁的基本力学性能以及设计计算方法的研究较少。

为此，本文基于平截面假定和UHPC受压应力应变关系方程，结合DBJ 43/T 325—2017《活性粉末混凝土结构技术规程》和T/CCPA 35—2022《超高性能混凝土结构设计规程》的极限承载力计算值，从理论分析和数值模拟2个方面对素UHPC梁受弯承载性能进行研究，推导出素UHPC梁开裂弯矩和极限承载力计算公式，可为素UHPC结构设计提供一定参考。

1 计算假定

由于考虑截面受拉区UHPC的抗拉作用，UHPC梁正截面承载力计算与普通钢筋混凝土构件不同。在分析UHPC梁正截面受力全过程时，需要建立以下2点假设：

（1）平截面假定

在UHPC梁正截面受力全过程中，梁跨中截面近似保持为平面。因此，采用平截面假定，可便于建立计算模型。

（2）UHPC受压应力应变关系

本文采用杜任远[13]的UHPC受压应力应变关系方程，如式（1）所示：

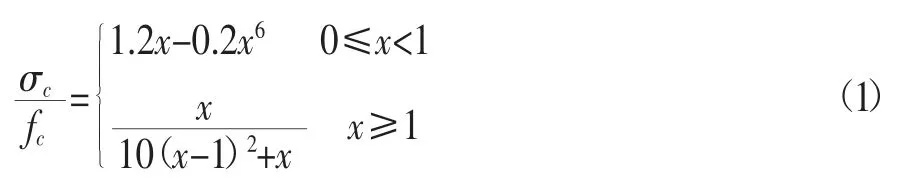
式中：σc——混凝土应变为εc时的应力，MPa；

fc——混凝土的轴心抗压强度，MPa；

定义x=εc/ε0，ε0为混凝土的峰值压应变，με。

2 UHPC梁承载能力计算

2.1 UHPC梁设计

为了便于计算分析，素UHPC梁设计采用矩形截面，结构形式为简支，梁体长1.2 m、宽0.15 m、高0.3 m。梁在支座两侧各悬出15 cm，计算跨度为0.9 m。UHPC轴心抗压强度取123 MPa，轴心抗拉强度取10.55 MPa。

2.2 开裂弯矩计算

为简化计算，采取与普通钢筋混凝土构件相同的方法，将纵向受力钢筋等效为相同模量的UHPC面积，此时UHPC梁可视为均质弹性材料。

引入截面抵抗矩塑性影响系数γ，用材料力学原理建立抗裂公式，则Mcr计算公式为：

式中：Mcr——素UHPC梁的开裂弯矩，kN·m；

γ——UHPC梁截面抵抗矩塑性影响系数；

ftk——UHPC的峰值拉应力，MPa；

W0——截面对受拉边缘的弹性抵抗矩，m3。

本UHPC梁未配置钢筋，故换算后的截面面积A0为：

截面重心距受压区边缘的距离x0为：

截面对形心主轴的惯性矩I0为：

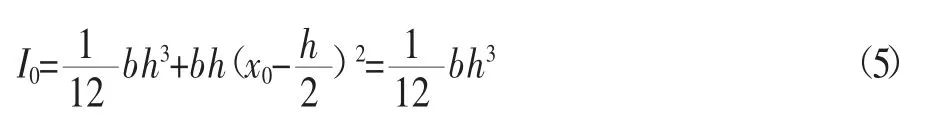
截面弹性抵抗矩W0为：

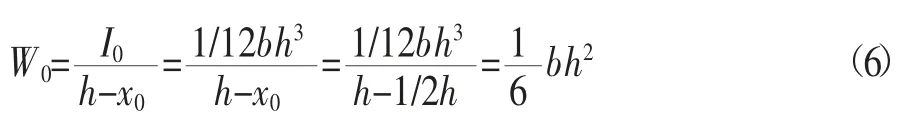
截面抵抗矩塑性影响系数γ为：

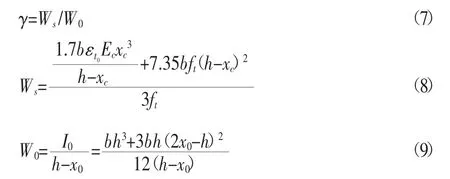
式中：b——UHPC梁体宽度，m；

h——UHPC梁体高度，m；

Ws——考虑受拉区塑性变形影响的梁截面弹性抵抗矩，m3；

xc——UHPC受压区高度，m；

εt0——UHPC初裂拉应变，με；

Ec——UHPC弹性模量，GPa；

ft——UHPC抗拉强度，MPa。

由于未进行试验，初裂拉应变εt0未知，因此采用已有经验公式进行截面抵抗矩系数的计算。文献[14]指出，棱柱体抗压强度为100 MPa左右的UHPC矩形截面梁的抵抗矩影响系数与配筋率的计算公式为：

由于本UHPC梁未配筋，则有：

除截面配筋率外，影响截面抵抗矩影响系数γ取值的还有截面高度、截面形状、钢纤维类别及体积掺量等因素。当截面高度发生变化时，采用公式（12）计算截面抵抗矩塑性影响系数。

联合公式（2）、（6）、（12）计算可得，开裂弯矩Mcr=28.72 kN·m。

2.3 极限承载能力计算

在计算UHPC梁正截面受弯承载力时，为简化计算，采取与普通钢筋混凝土构件相同的方法，将UHPC应力图形等效为矩形应力图形[15]。

（1）正截面受压区应力简化

受压区混凝土压应力合力Fc为：

压应力合力Fc到中和轴的距离：

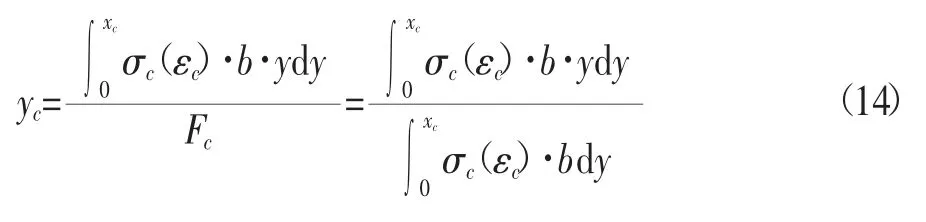
距离中和轴y处的混凝土压应变为：

压应力合力Fc变化为：

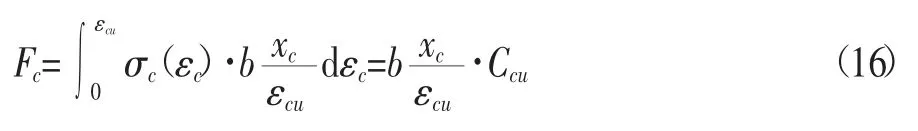
合力Fc到中和轴的距离变化为：

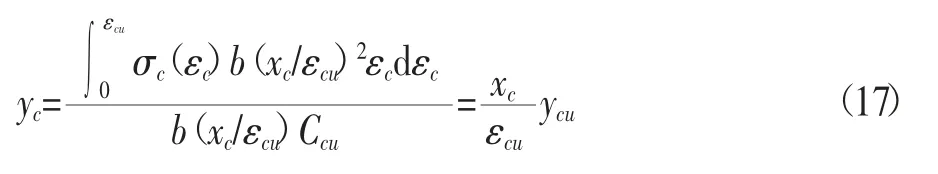
式中：εcu——混凝土的极限压应变，με；

Ccu——受压区UHPC应力-应变关系曲线所围的面积，MPa；

ycu——面积形心到坐标原点O的距离，με。

则有：

根据UHPC受压本构关系方程式（1），则有：

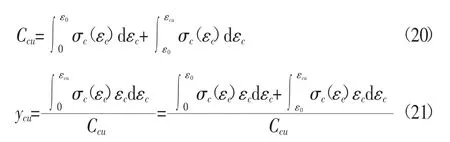
引入参数k1、k2满足：

受压区混凝土承担的弯矩：

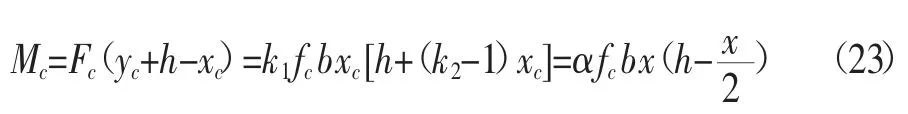
式中：fc——UHPC抗压强度，MPa；

x——受压区等效应力高度，m。

其中：

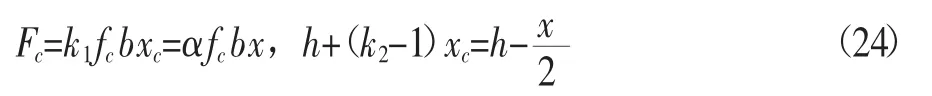
引入参数β，满足：

则有：

解得α=0.89，β=0.81，则UHPC受压区等效矩形应力高度为0.81xc，应力大小为0.89fc。

（2）正截面受拉区应力简化

受拉区高度：

由平衡条件可得：

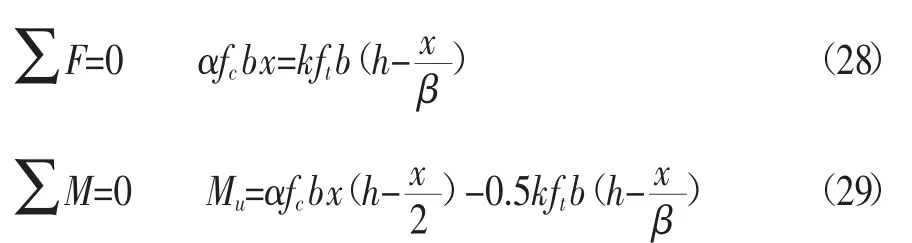
素UHPC梁破坏时，极限弯矩与开裂弯矩相等，即Mut=Mcr。

联立公式（28）、（29）可得等效受压区高度x的表达式：

其中：

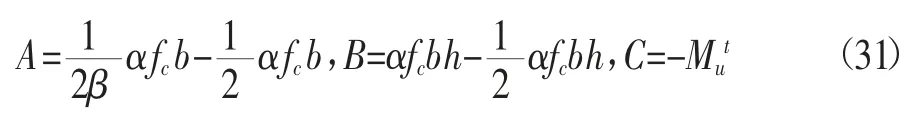
故等效受压区高度x=11.56 mm。

代入公式（28）可得，受拉区等效系数k=0.42。考虑一定的安全储备，受拉区等效系数k取0.35。

所以，截面受弯极限承载力计算公式为：

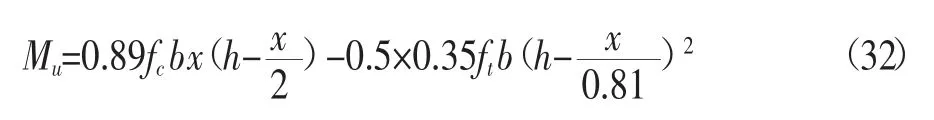
代入数据可得极限承载力Mu=33.24 kN·m。

2.4 DBJ 43/T 325—2017极限承载能力计算

DBJ 43/T 325—2017中UHPC单轴受压应力应变关系式为：

UHPC轴心抗压强度标准值fcu=127.23 MPa。

立方体抗压强度标准值fcu，k=1.45fcu=184.48 MPa。其中：

由公式（25）、（26）可得，α1=0.86，β1=0.70。

相对界限受压区高度：

受弯构件的正截面受弯承载力计算应符合以下规定：

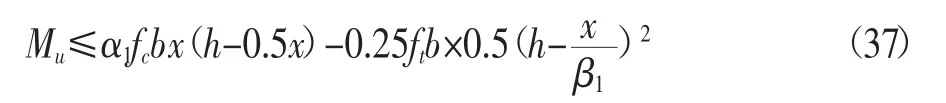
混凝土受压区高度x由以下公式确定：

代入数据可得等效受压区高度x=7.22 mm。

混凝土受压区高度还应符合以下条件：

由公式（37）可得，极限承载力Mu=17.35 kN·m。

2.5 T/CCPA 35—2022极限承载能力计算

受弯构件的正截面受弯承载力按下列公式计算：

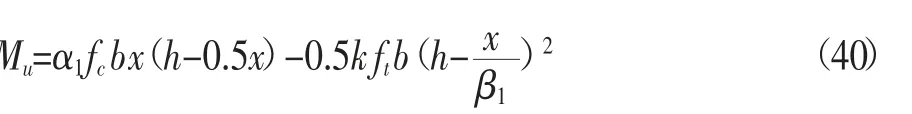
式中：α1——非均匀受力时，UHPC受压区应力图形可等效为矩形，等效应力值的影响系数，取0.75；

x——UHPC受压区等效矩形应力图形的高度，m；

k——UHPC受拉区等效应力的折减系数，取0.25；

β1——受压区UHPC矩形应力图高度x与中和轴高度xn的比值，取0.75。

由公式（36）可得UHPC构件的相对界限受压区高度ξb。

混凝土受压区高度x由以下公式确定：

代入数据可得等效受压区高度x=8.26 mm。

混凝土受压区高度还应符合以下条件：

由公式（40）可得极限承载力Mu=17.30 kN·m。

综上，素UHPC梁的开裂弯矩为28.72 kN·m，极限承载力为33.24 kN·m，而按照DBJ 43/T 325—2017及T/CCPA 35—2022计算的极限承载力偏小，分别为17.35、17.30 kN·m。

3 试验梁有限元分析

为了更全面了解UHPC梁在荷载作用下结构整体的应力状态和变形，选取通用有限元软件ABAQUS作为分析软件，在ABAQUS/CAE模块中建模，通过ABAQUS/Standard模块对此构件进行计算和分析。

3.1 单元类型选取

为了确保模型梁位移变化的计算精度，UHPC梁采用八节点减缩积分单元（C3D8R）进行模拟。

3.2 单元网格划分

有限元网格划分是进行数值模拟分析重要的一步，直接影响后续数值计算的求解精度、求解收敛性和求解速度。网格划分过于密集会使计算时间过长，过于稀疏则无法满足分析要求。因此有必要采用合适的网格划分技术来确定网格尺寸。

本文采用ABAQUS提供的结构化网格划分技术来确定网格尺寸。首先确定合理的初始网格大小，采用全局布种与边界布种相结合的方式，通过不断细化网格对模拟结果进行分析。最终确定模型梁梁体的网格尺寸为15 mm，由于金属垫块不是主要的分析对象，因此网格尺寸设置为20 mm，模型梁的网格划分如图1所示。

图1 UHPC梁有限元计算模型

3.3 相互作用及边界条件

根据加载实际情况进行简化，为了避免应力集中现象，将金属垫块设置在加载点位置处，金属垫块与梁体通过绑定约束（tie）连接，在金属垫块与支座之间建立相应的参考点（RP）。在跨中截面设置参考点，监测跨中弯矩的变化，并通过耦合约束（coupling）将参考点与金属垫块支座相连接。为了充分还原简支约束，左端支座约束：U2=0，右端支座约束：U2=U3=0。

3.4 加载方式

本次分析中共设置了2个分析步（step）。

第一步（step1）中施加重力荷载，混凝土容重采用24 kN/m3，重力加速度取9.8 m/s2。

第二步（step2）施加位移荷载20 mm。为了更好地反映结构构件在加载过程中产生的塑性变化，采用位移加载20 mm的方式。

3.5 材料性能

本文采用混凝土塑性损伤模型，参考傅元方[16]的做法：混凝土抗压强度取123 MPa，抗拉强度取10.55 MPa，密度取2400 kg/m3，初始弹性模量取39.8 GPa，泊松比取0.2。应力-应变关系和受拉损伤因子的计算均采用张涛[17]的计算公式。

塑性参数中，剪胀角取30°，流动势偏移量取0.1，双轴受压和单轴受压极限强度比（fb0/fc0）取1.16，不变量应力比（Kc）取0.6667，粘滞系数取0.0005。塑性损伤模型参数见表1、表2。

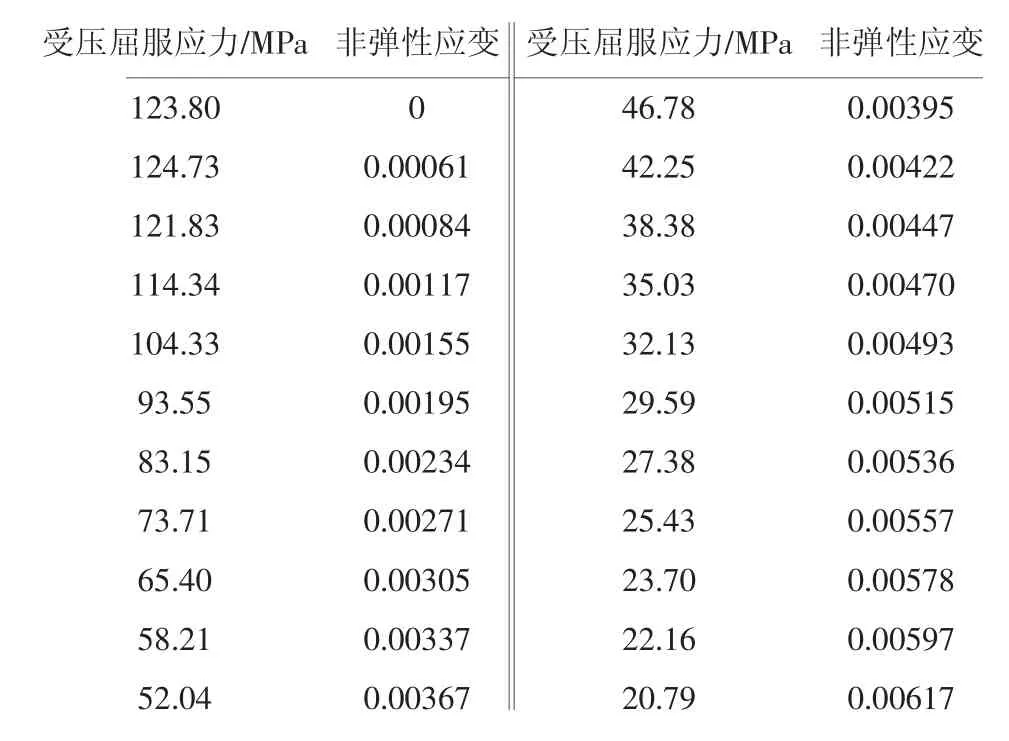
表1 受压应力-应变关系

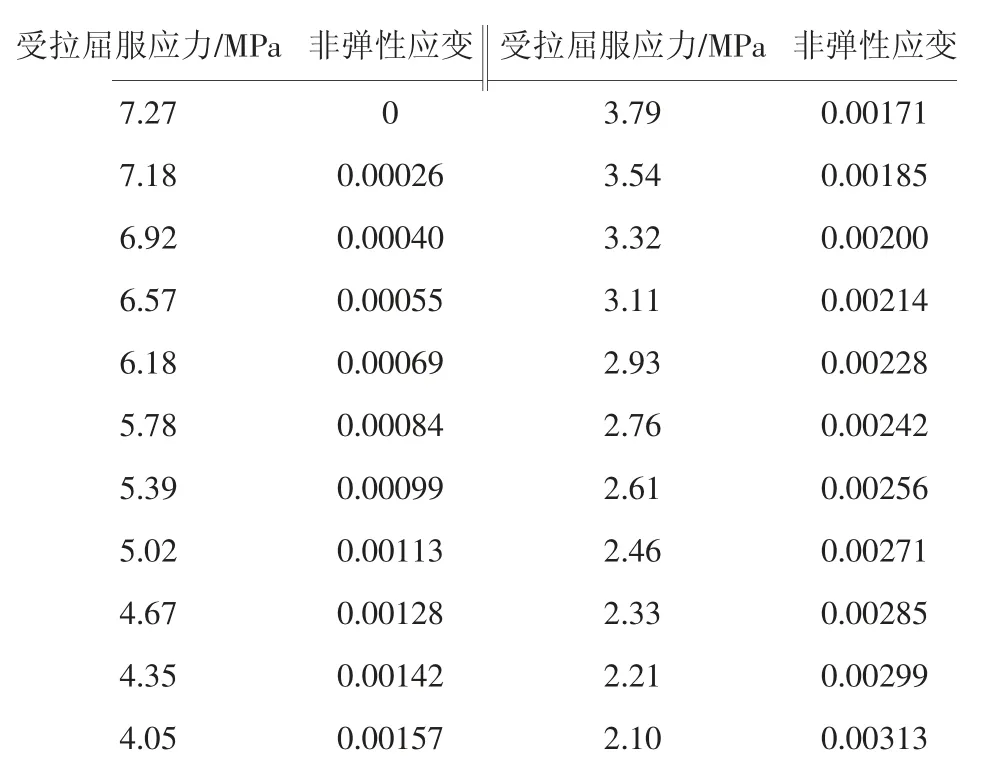
表2 受拉应力-应变关系

3.6 有限元计算结果分析

3.6.1 荷载位移曲线及弯矩历程曲线

为了直观地看出在有限元模拟条件下模型梁荷载与位移之间的关系，绘制了梁体跨中截面的荷载-位移曲线，以及位移加载过程中的跨中弯矩随加载历程的变化曲线，如图2、图3所示。

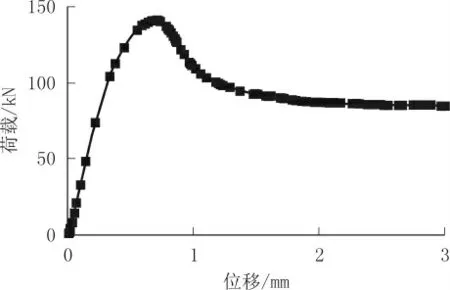
图2 梁体跨中截面的荷载-位移曲线

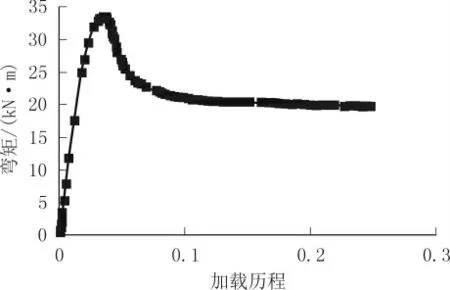
图3 弯矩随加载历程变化曲线

由图2可见，荷载-位移曲线较好地展示了UHPC梁受弯的全过程受力状态，由于建模过程中没有配置钢筋，在两点加载达到120 kN左右时，挠度为0.5 mm，此时开始出现微小裂缝；两点加载达到140 kN左右时，挠度为1.0 mm，此时达到极限承载力状态。表3为公式计算值与有限元模拟值的结果对比。

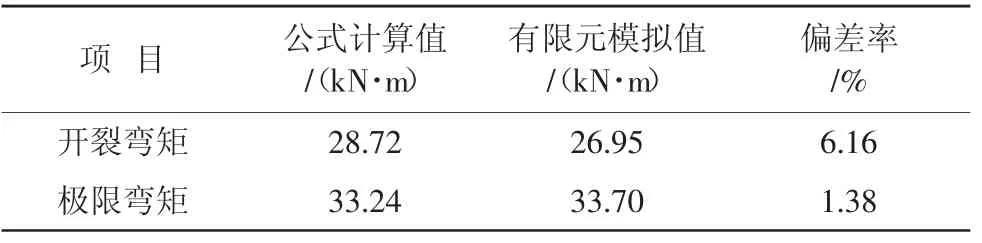
表3 公式计算值与有限元模拟值结果对比

由表3可以看出，数值模拟计算结果和公式计算结果非常接近，开裂弯矩和极限弯矩的偏差率仅为6.16%、1.38%。

总的来说，素UHPC梁与配筋混凝土梁相比，塑性虽然存在不足，但开裂弯矩和极限弯矩相较于普通钢筋混凝土梁有一定程度的提高，所以超高性能混凝土的应用可以提高结构的承载能力。

3.6.2 塑性损伤云图（见图4）

图4 模型梁塑性损伤云图

由图4可见，随着位移荷载的施加，在位移较小时，裂缝首先出现在跨中纯弯曲段，并沿着梁高方向不断向上扩张；随着位移的增加，纯弯曲段不断产生新的裂缝，原有的裂缝不断扩张，达到设定的受拉损伤最大值时，最大裂缝高度发展停滞，最终达到极限承载力，模型梁破坏。

总的来说，这种破坏模式不同于传统的钢筋混凝土梁，模型梁主要在纯弯曲段产生了较大的混凝土损伤。本模型由于研究简支约束，对两端支座约束较少，弯剪段混凝土损伤较小，斜裂缝几乎没有产生，就沿着跨中的裂缝达到极限承载能力。由于有限元模拟中精确定义混凝土内部初始缺陷难度很大，应力应变数据、塑性损伤因子等都很难充分还原结构实际的受力性能，导致有限元模拟结果存在一定的局限性。

由有限元模拟结果可知，采用本文推导的计算公式得出的开裂弯矩计算值、极限弯矩计算值与有限元模拟值的偏差率仅分别为6.16%和1.38%，公式计算结果与有限元模拟结果接近。而运用DBJ 43/T 325—2017和T/CCPA 35—2022计算的极限弯矩值偏小，约为有限元模拟值的一半。因此，本文的计算公式可适用于素UHPC梁开裂弯矩以及极限承载能力的计算，同时可为素UHPC结构设计提供一定参考。

4 结语

（1）开裂弯矩计算中，将纵向受力钢筋等效为相同弹性模量的UHPC面积时，可将UHPC梁视为均质弹性材料，结合经验公式，推导出UHPC梁开裂弯矩计算公式，公式计算值与有限元模拟值吻合良好。

（2）极限承载力计算中，采用与普通钢筋混凝土相同的方法，将UHPC应力图形等效为矩形应力图形，推导出UHPC梁极限承载力计算公式，公式计算值与有限元模拟值吻合良好。

（3）选取通用有限元软件ABAQUS对素UHPC梁建立数值分析模型，有限元模拟计算结果符合预期，UHPC梁开裂弯矩和极限弯矩与计算值接近，在一定程度上验证了计算方法的可靠性。

（4）采用DBJ 43/T 325—2017及T/CCPA 35—2022计算的极限承载力偏小，本计算方法结果与有限元模拟结果相近。在实际工程应用中，结合一定足尺试验的基础上，应用本计算方法可以充分发挥超高性能混凝土的力学性能，避免造成材料浪费。