泥皮作用下的地连墙槽壁稳定性分析

刘卫卫，唐建政，赵民 （济南市勘察测绘研究院，山东 济南 250101）

1 引言

21世纪是地下空间资源大力开发利用的新纪元，近年来我国的地下工程不断向“长洞线、大埋深、高应力”方向发展[1]。随着地下工程的深入发展，工程种类越来越多，面临的地质环境越来越复杂，因此地下工程在开挖过程中面临的安全问题就越来越多，尤其是深厚软黏土及砂土中，在黏土或砂土层中成槽时，槽壁因临空而失稳，对基槽的安全性造成了极大的威胁，在施工中往往采用向槽内注入泥浆的方法来保持槽壁的稳定。事实上，泥浆槽壁的稳定过程就是泥浆与地基土相互作用和影响的过程。实际工程施工过程中，经常采用泥浆护壁方法保持侧壁的稳定性，效果比较明显，应用广泛。但其作用机理少有学者研究，因此，护壁泥浆对槽壁作用机理的研究，对进一步推广泥浆护壁应用具有极其重要的作用。

泥浆液对槽壁稳定的影响可以概括为两点：其一，泥浆的液柱压力主要靠泥浆比重来调节，液柱压力随比重增大，越大槽壁越稳定；其二，泥浆的渗透胶结作用，泥浆压力与地下水压力及土压力产生的压差将会使泥浆渗透进入地层，在槽壁上形成泥皮且其高分子材料渗入到土体内胶结土体颗粒，以增强土体的内聚力[2]，这是提高泥浆护壁防塌性能最重要的一个因素。

2 泥皮作用下的槽壁稳定分析

2.1 力学分析

在没有泥皮的情况下，力学示意图如图1所示，图（a）、（b）中的泥浆水平力均可以用以下公式计算。

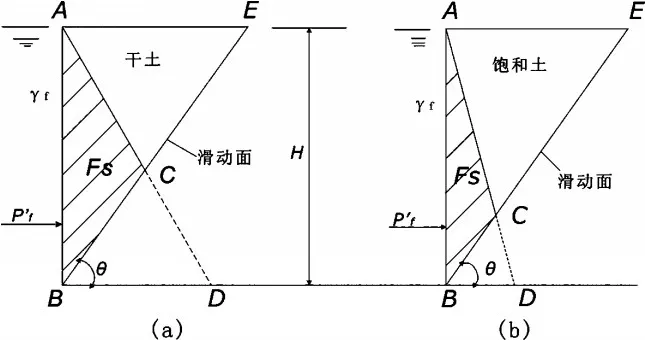
图1 计算示意图

如果用Fs表示△ABC区域的面积，则：

还可以得出：

2.2 泥皮抗剪强度试验

由于泥浆失水而在槽壁上形成泥皮时，泥浆的实际压力介于Pf和之间。泥皮的密度、强度和变形特性与所使用的膨润土性能和用量以及地层条件有着密切关系。在研究中用三轴剪切固结不排水模型试验来确定泥皮的抵抗变形能力。

采用直径72mm，高130mm的砂土试样，在膨润土泥浆中浸泡12h，在其表面形成一层泥皮，如图2所示。

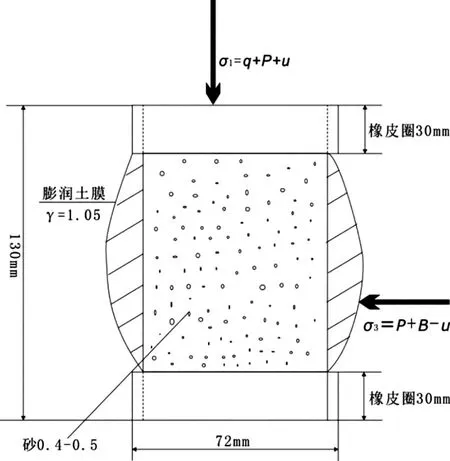
图2 试验砂样

采用三轴固结排水剪切试验，试验过程中试样虽发生变形，但仍与泥皮结合。砂土试样表面的抗剪强度试验值为0.74N/cm2（图 3）。虽然这个力比较小，但却能在一定程度上防止砂子松散坍塌。即使泥皮抗剪强度很小，也可以支持一个位于砂砾地层没有护壁泥浆的高约2m～3m的沟槽，而不会发生坍塌，这说明，槽壁上形成泥皮时，受泥皮影响其稳定性大大增加。

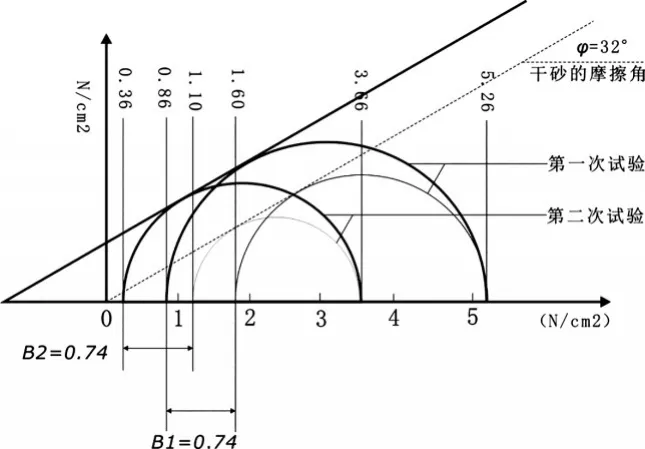
图3 带有泥皮的砂样三轴试验结果

2.3 泥浆抗剪强度下稳定性分析

从物理现象的角度观察槽壁的稳定性，当土颗粒有从槽壁面上脱落进入泥浆的趋势时，膨润土泥浆对此有微弱的抵抗作用。为了模拟土颗粒进入泥浆受到的阻力作用，本文建立模型可以将此作为两块硬板间的全塑性体的压缩问题处理，进行以下分析。

取泥浆的微小单元加以研究，其平衡方程。

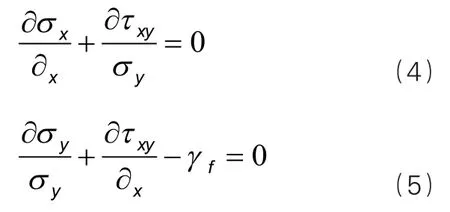
式中：γf为凝胶状态时的泥浆容重。

经过模拟分析，当微分体应力状态满足下列屈服条件时，泥浆将发生塑性流动。

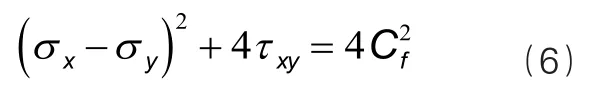
式中：Cf为泥浆凝胶的抗剪强度。

在合适的边界条件下，以上2个公式可以求得静力状态下的应力。对于宽度为2a的深槽，水平应力：

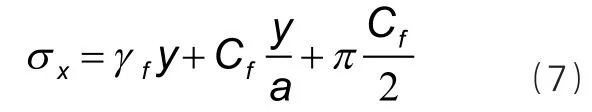
被动抗力：

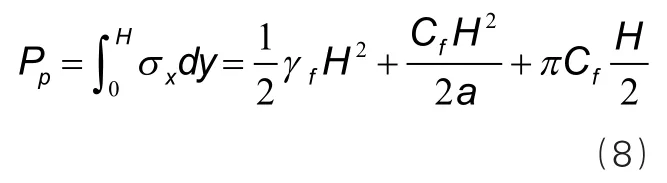
因此，对于黏性土中的深槽，经过推导，可采取以下公式（9）推算其安全系数：

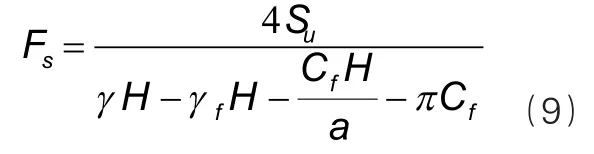
由以上公式可以看出，即使泥浆只有极小的抗剪强度，对于增加槽壁稳定性也有一定的作用。

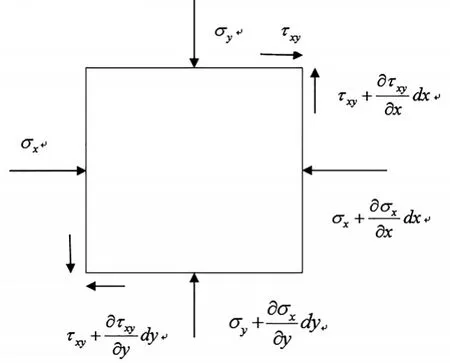
图4 泥浆微小单元

因为地层的土拱效应和泥浆抗剪强度能够有效地提高地下连续墙的槽壁稳定性，所以采用“考虑土拱效应和泥浆抗剪强度作用下的稳定性分析”的方法[2]，对槽壁稳定性安全系数进行如下分析：

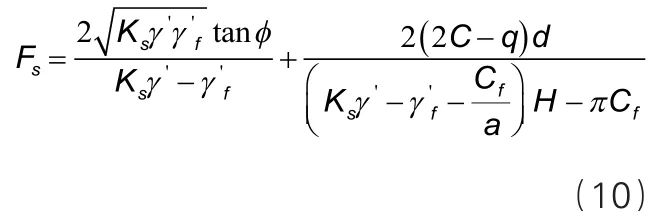
式中，γ'、分别为槽壁土层和泥浆的浮容重，kN/m3；d为地下水深度，m；φ为土层的不排水抗剪强度；Cf为泥浆抗剪强度，kPa；a为槽宽的1/2，m；H为槽深，m；q为上部施工荷载，kN/m2；Ks为拱效应折减系数（取值为0.1～0.25）。对于膨润土泥浆其抗剪强度Cf，一般为0.245kPa。

选取多组数据多种工况，采用该方法进行分析计算，得出的结果如表1所示。

泥皮作用下安全系数计算 表1

3 泥皮增强槽壁稳定性计算

本文采用三棱柱模型计算[4-6]与泥皮抗剪强度模型计算相对比。

三棱柱模型考虑的计算参数：成槽长度、地基土天然重度、地基土浮容重、地下水深度、开挖深度、泥浆液面高度、土体的内摩擦角、黏聚力和泥浆重度。

通常情况下，泥皮抗剪强度作用下的分析模型考虑的计算参数：成槽宽度、成槽深度、地基土浮容重、地下水深度、泥浆浮容重、土体内摩擦角、黏聚力、地面载荷、拱效应系数和泥浆抗剪强度。这些条件对于泥浆的作用机理影响很大，不同的地下水深度，对于泥浆的稠度设置不同，土颗粒的粗细，如粗砂、细砂对于泥浆的用量也不同，因此，模型应控制好外界条件，对于模型计算的精确度影响比较大。

其中，从计算参数来看，三棱柱模型考虑泥浆液面高度对槽壁稳定的影响。而另一种方法则考虑了地面施工载荷、泥皮抗剪强度和土拱效应，其因素对于槽壁稳定均有一定影响，泥浆液面的高度低于水位，槽壁稳定性相比泥浆液面高的槽壁稳定性相对较差。地面施工荷载越大泥浆护壁对于槽壁的稳定性作用越明显，相应的泥皮抗剪强度较大，土拱效应相对比较明显，两种方法各有利弊。将典型地层分析中所得出的土层物理力学参数分别代入，进行两种分析方法的计算对比，计算过程及结果对比详见表2所示。

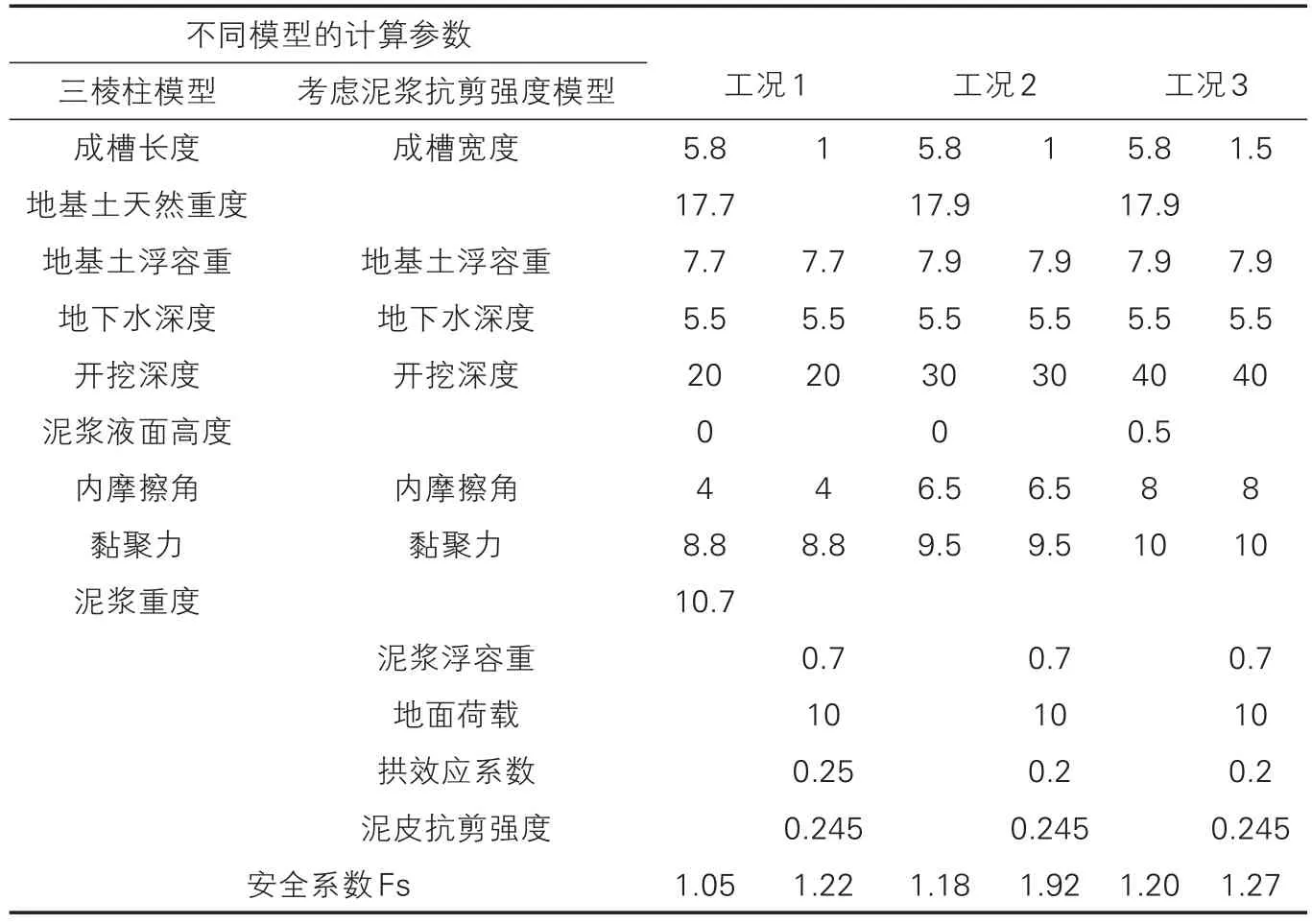
两种模型计算结果对比 表2

从表2不同分析方法及不同工况计算结论分析对比可知，采用泥浆抗剪强度计算模型安全系数高于采用三棱柱模型计算得出的安全系数，两种模型的内摩擦角变化基本不变，大小相同，相差较大的主要是黏聚力，采用泥浆抗剪强度计算模型所计算得出的黏聚力大于采用三棱柱模型计算得出的黏聚力，对于安全系数的提高起到了重要作用。根据两种模型计算工况，监测某工程基槽稳定性，通过实际工程的变形监测数据对比，其安全稳定性与采用泥浆抗剪强度计算模型理论得出的安全系数结论相吻合，因此，采用考虑泥浆抗剪强度模型更接近工程实际。

4 结语

①通过对比计算分析，槽壁在泥浆的作用下，失水后的泥浆在槽壁表面会形成致密的泥皮，通过力学分析和三轴固结排水试验表明，泥皮的抗剪强度虽小，但却能够很大程度地提高槽壁稳定性，确保基坑的安全稳定性。

②采用三菱柱计算模型与泥皮抗剪强度计算模型相对比，在考虑泥皮抗剪强度的基础上，其计算出的安全系数更接近实际情况，表明泥浆作用于槽壁能提高槽壁的稳定性，同时能更准确地确定泥浆的比重参数，节约工程预算。

③考虑泥浆作用下槽壁稳定性相比无泥浆作用可进一步提升，泥浆护壁作用机理即通过浆液将泥皮渗入到松散槽壁中，形成新的稳定槽壁，从而提升了槽壁的稳定性，其对相似地下工程坑壁提升稳定性具有重要参考意义。