提高冲碾机跟踪规划路径精度的方法

宋二波，姚仰平

(北京航空航天大学 交通科学与工程学院，北京 100191)

压路机作为一种典型的土石方压实机械，在机场高填方工程中发挥着重要作用，为了降低作业人员的劳动强度，同时提高压实效率，无人驾驶冲击压路机的发展成为一种有效解决方案。

路径规划和路径跟踪是无人驾驶压路机中2 个重要的问题。根据施工现场的情况，在地头转向处均采用圆弧过渡，如文献[1-3]，这种转向满足了冲碾机的最小转弯半径要求，且易于规划，但冲碾机在该处附近常产生较大跟踪误差，从而影响碾压工作面的压实质量。分析其原因主要是由于冲碾机的规划路径曲率不连续使得控制器中方向偏差和横向偏差发生了突变，从而造成输出转角控制量发生了突变，跟踪误差增大。因此，研究的重点是优化地头转向路径，以提高冲碾机地头转向的跟踪精度。

由于主要研究是针对冲碾机的地头转向段进行轨迹优化，而农业中有关地头转向[4-5]的研究已较为成熟。目前对于路径光滑化的处理方法主要用曲线拟合的方法，常用的光滑曲线有3 次B 样条曲线、β 样条曲线、贝塞尔曲线、回旋曲线及广义初等曲线等。Song 和Zhang[6]针对无人压路机规划路径中存在曲率不连续的问题，采用了3 次B 样条曲线拟合的方法对规划路径进行了平滑处理。Gómez-Bravo 等[7]在自动泊车系统中利用β 样条曲线生成了曲率连续无碰撞的路径。Dong 等[8]利用Bézier 曲线实现了2 条直线间的平滑过渡。Backman等[9]指出Dubins 曲线的缺陷，引入了回旋线，以生成地头转向平滑路径，该路径的曲率和速度都连续，且综合考虑了车辆的最大转向率和最大加速度。Graf Plessen 和Bemporad[10]参考回旋曲线，生成了广义初等路径和双初等路径，对规划的轨迹进行了平滑处理，有效的解决了农田覆盖参考路径的尖锐点问题。

本文的目的是提高冲碾机跟踪规划路径的精度，因此以原规划路径为目标路径，优化方法采用广义初等路径和双初等路径，要求优化后的路径不仅光滑且曲率连续，还需邻近原规划路径。综合考虑以上2 个要求，提出了一种符合冲碾机作业的地头转向路径优化方法。

1 冲碾机压实工艺

冲击式压路机通过专用牵引车牵动冲击轮，利用冲击轮自身的质量及滚动前进的冲击力，对填方土体进行静压和冲击，使土体被均匀压实。目前根据现场施工的情况，对于施工路面宽度≥24 m 的工况，主要采用“环形针环跑”（U 型）路线，地头转向处采用U 型转向，符合冲碾机最小转向半径的要求，而对于路面宽度<24 m 的工况，则需要采用一种“大骨头绕跑”（Ω 型）的路线，地头转向处出现Ω 型转向，如图1 所示。

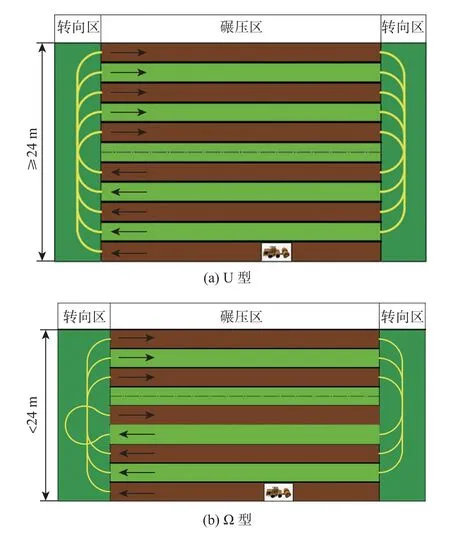
图1 冲碾机转向方式Fig. 1 Headland turning mode of impact roller

在机场高填方工程中，考虑压实效果和作业效率，冲碾机压实工艺主要有错轮碾压和错峰碾压。以25 kJ 的冲击压路机为研究对象，轮宽lv为0.9 m，两轮内边距ld为1.17 m，冲击轮错轮碾一遍为整体碾压一遍，因此冲碾工作面宽度l为4 m。错轮碾压[3]形成的理论间隙 (ld-lv)/2为0.13 m，如图2（a）所示。冲碾轮周长CS为4.8 m，两谷底或峰顶之间的距离 Δd=CS/3为1.6 m，每遍错轮为1/6，5 遍完成错峰碾压，达到冲击压实质量均匀的效果。错峰碾压如图2（b）所示。

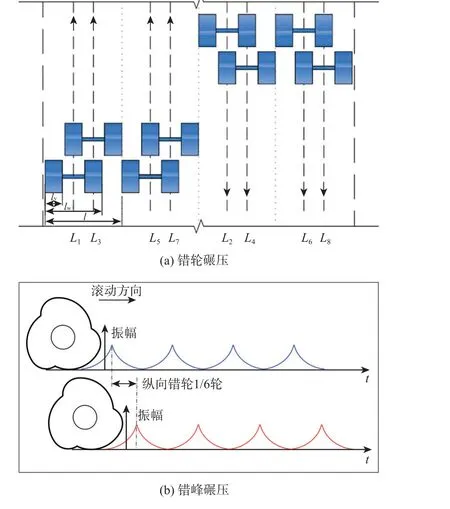
图2 冲碾机压实工艺Fig. 2 Compaction technology of impact roller

2 冲碾机U 型转向路径优化

冲碾机U 型转向路径是在直线和直线之间采用圆弧过渡，因此，转向路径存在曲率不连续的问题，参照广义初等曲线曲率连续的特点，利用广义初等曲线来构造过渡曲线，由于对称性，以U 型转向路径的1/2 部分进行分析讨论。

2.1 广义初等曲线特性

1） 连续性。广义初等曲线由入口回旋曲线、过渡圆弧及出口回旋曲线组成。广义初等曲线曲率分布呈梯形状。其中，λ为圆弧弧长Lh与曲线总长度L的比值。广义初等曲线曲率κ如图3（a）所示。

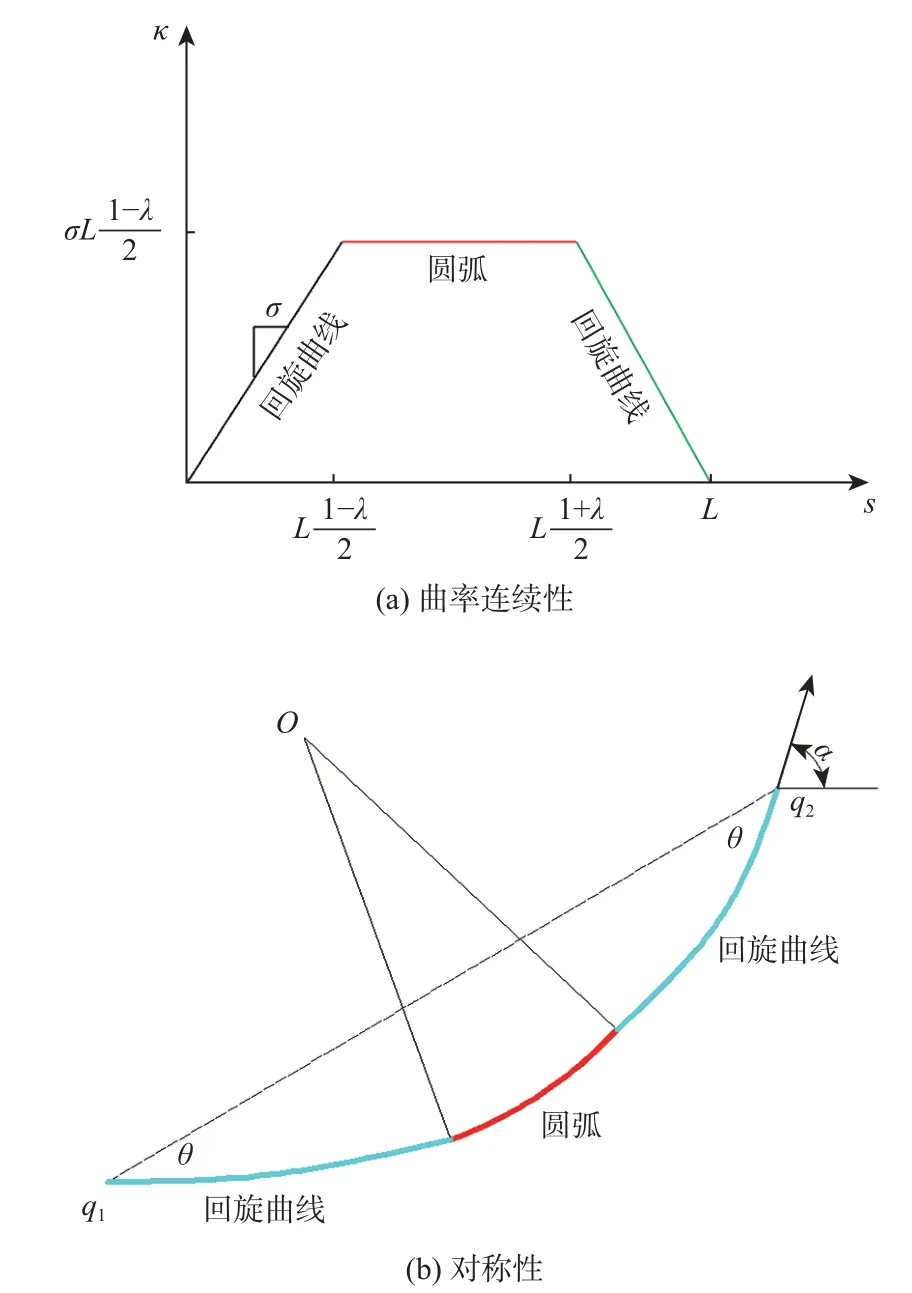
图3 广义初等路径Fig. 3 Generalized elementary path

文献[10]有构造曲线相关的计算方法如下：

式中：d为2 点直线距离；（x1，y1）为起点坐标；（x2，y2）为终点坐标； ψ (z)为回旋曲线的方向角。

广义初等曲线虽然光滑，但在构造过程中并未考虑曲率的约束，2.2 节与2.3 节将结合冲碾机实际工况对U 型转向路径进行优化，且从广义初等曲线的构造方法角度进行了总结分析。

2.2 基于广义初等曲线的U 型转向路径构造方法1

在参考文献[10]中已证得，起始点坐标相同的条件下，广义初等曲线可替代圆弧，且起始点状态都与圆弧保持一致。方法1 中R表示可替代的圆弧半径，并以R和λ为参数，先确定回旋线，再确定过渡圆弧。设冲碾机的原规划路径为圆弧R=6 m，根据广义初等曲线的定义，在不同（R,λ）组合中根据2.2.1 节约束条件筛选有效路径。

2.2.1 满足冲碾机转向约束

由广义初等曲线的定义，广义初等曲线圆弧半径R为

式中：Rmin为最小转弯半径。

R一定，λ分别取值0、0.2、0.5、0.7、1，λ一定，R分别取值6 m, 7 m, 8 m，共组合为15 组不同的（R,λ）组合曲线。得到的广义初等路径的规律均一致，如图4 所示，其中Line 表示y＝0 m 和x＝12 m 的2 条直线。假定冲碾机的最小转弯半径Rmin=6 m，得到符合冲碾机转向约束的路径组合（R,λ）。

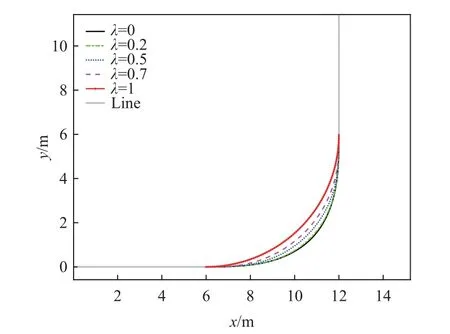
图4 R=6 m 不同λ 取值的广义初等曲线Fig. 4 Generalized elementary curves with different λ for R=6 m

由于D是关于λ的隐式函数，λ若条件给定则D确定。因此，对于不同λ取值的R有条件约束，如表1 所示。

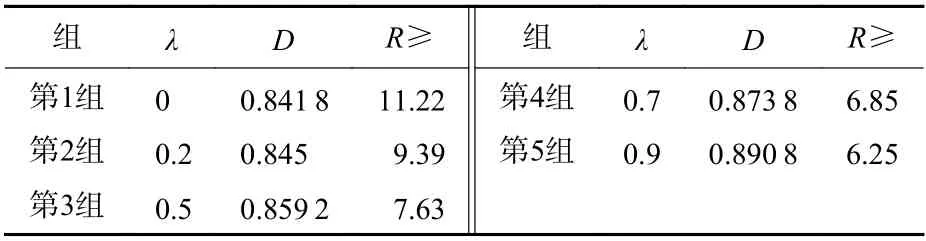
表1 不同λ 值的R 约束值Table 1 R constraint values with different λ values

2.2.2 邻近目标路径

由于跟踪的目标路径是原规划路径，设原规划路径为p，优化后的路径为p*，实际跟踪后的轨迹为p′，因此需要 减 小p′与p的距离，即让dist|p′-p|最小化，而实际的跟踪误差是 d ist|p′-p*|。因此，只有当 dist|p-p′|≈0时，实际的跟踪误差才是跟踪规划路径的误差。

设定一个阈值 Δε，即远离规划路径的上限值，则筛选路径的标准如下：

在优化后的路径组合中寻找符合邻近目标路径条件的组合，有（8 m,0.5）和（7 m,0.7），如图5 所示。

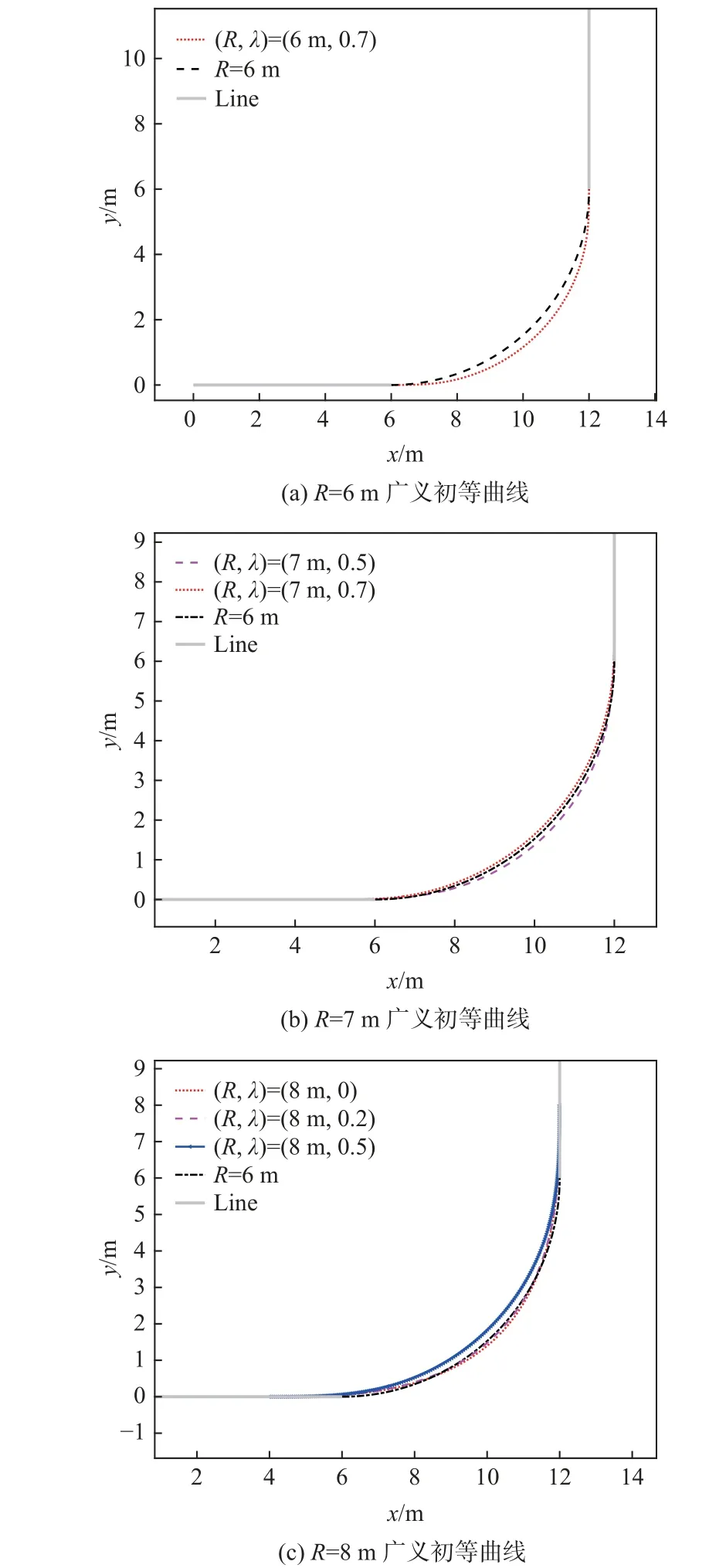
图5 方法1 得到的与R=6 m 相近的路径Fig. 5 Paths close to R=6 m by method 1

2.3 基于广义初等曲线的U 型路径构造方法2

2.3.1 广义初等曲线构造方法2

文献[12]中利用广义初等曲线来连接2 条定向的直线段，如图6 所示。根据文中的算法，R表示过渡圆弧半径，并以R和λ为参数先确定过渡圆弧，再确定回旋线。为区别第1 种构造曲线的方法，以下均采用R′表示。

图6 连接两直线的过渡曲线Fig. 6 Transition curve used to connect two straight stretches

式中：XL为回旋线在x方向上的增量；YL为回旋线在y方向上的增量。

4） 计算切点位置：设定的冲碾机的最小转向半径为6 m，以R′≥6 m为约束条件，分别取（R′, λ）组合进行对比分析。

2.3.2 满足冲碾机转向约束

设定圆弧的半径R′分别取3 种数值（6 m, 7 m,8 m），并 以R′一 定，λ分 别 取5 类 比 值（0,0.2,0.5,0.7,1），共组合15 组不同的（R′, λ）组合曲线。图7为R′=6 m时不同λ值下的曲线。

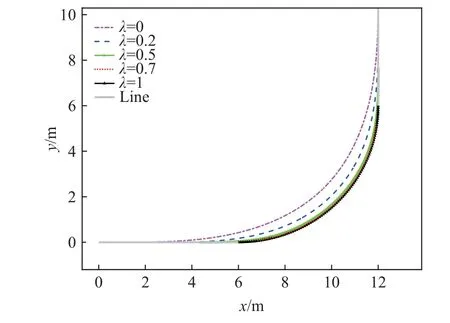
图7 R′=6 m不同λ 值的曲线Fig. 7 Generalized elementary curves with different λ for R′=6 m

2.3.3 邻近目标路径

与2.2 节方法判定邻近的方法相一致。在15 组的曲线中筛选得到邻近规划路径p*，有（5 m,0.2）、（6 m,0.5）和（6 m,0.7），如图8 所示。

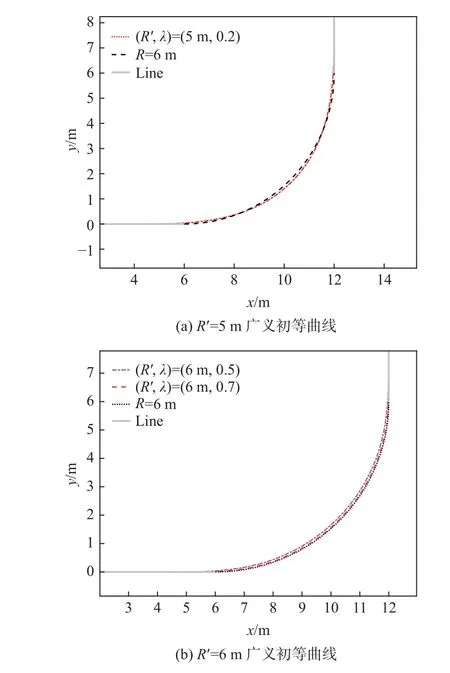
图8 方法2 得到的与R=6 m 相近的路径Fig. 8 Paths close to R=6 m by method 2

3 冲碾机Ω 型转向路径优化

冲碾机Ω 型转向路径是在地头宽度小于转向半径时所采用的转向方式，由圆弧连接组成，常用Dubins 算法生成，但是转向路径依旧存在曲率不连续的问题，参照双初等曲线可实现0°光滑过渡的特性，利用双初等曲线来构造Ω 型转向路径，并进行相应的分析讨论。

3.1 双初等曲线

双初等曲线[10]是由2 条广义初等曲线组成，定义为起始点PΩ1点和终点PΩ3点的航向相同，连接这2 点的路径称为双初等路径。

与广义初等曲线不同的是其参数γ的定义，γ的大小决定了连接点PΩ2。

双初等曲线主要因为其可圆滑的实现0°航向过渡，如图9 所示，但是其未考虑路径的曲率是否符合车辆转向曲率约束条件。

图9 不同γ 取值的双初等路径示意图Fig. 9 Schematic diagram of bi-elementary paths with different γ values

3.2 考虑Rmin 的双初等路径Ω 型转向

文献[10]针对农机的地头转向，采用的双初等路径来替代原先的圆弧，如图10（a）所示，没有考虑Rmin，其中Arc 表示半径为6 m 的半圆弧，Dubins为在满足曲率约束和规定的始端与末端的切线方向的条件下，连接2 个二维平面点的最短路径。因此在其基础上进行优化计算。

设双初等路径的起点坐标为PΩ1(0,0)，终点坐标为PΩ3(x3,y3)，中间点坐标为PΩ2(x2,y2)。可计算得到双初等路径的RΩmin。

因为D是α的函数，α又可通过PΩ3点求得，因此，当γ一定时，RΩmin是关于(x3,y3)的函数。

Rmin是冲碾机最小转向半径，因此有约束RΩmin≥Rmin，Rmin取6 m。当γ=0.5 时，得到一个可行解，从而得到（x3，y3）的坐标点。再以(x3,y3)为PΩ3点坐标，取不同的γ值，可得到曲线组合，如图10（b）所示。但路径在双初等曲线与圆弧的连接处曲率不连续。

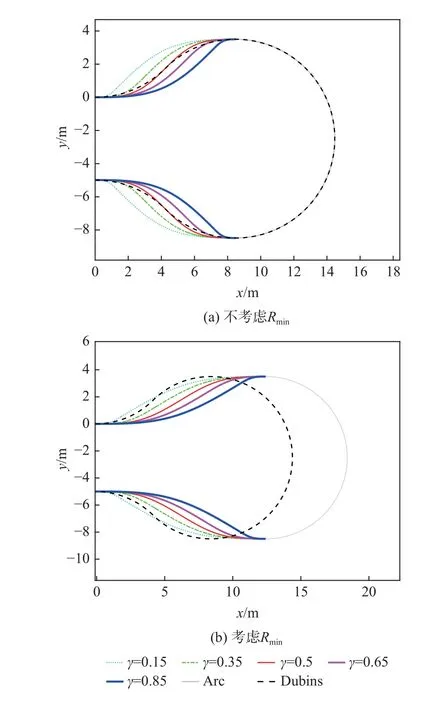
图10 不同γ 取值的Ω 型转向路径及曲率Fig. 10 Ω-shaped turning paths and curvature with different γ values

3.3 曲率连续的Ω 型转向路径

文献[13]中有对Ω 型转向路径的描述，如图11所 示，γ在0.5～0.65 范 围 内 构 造 路 径 与Dubins 路径相邻近，对该范围内γ路径进行优化，使其曲率连续：

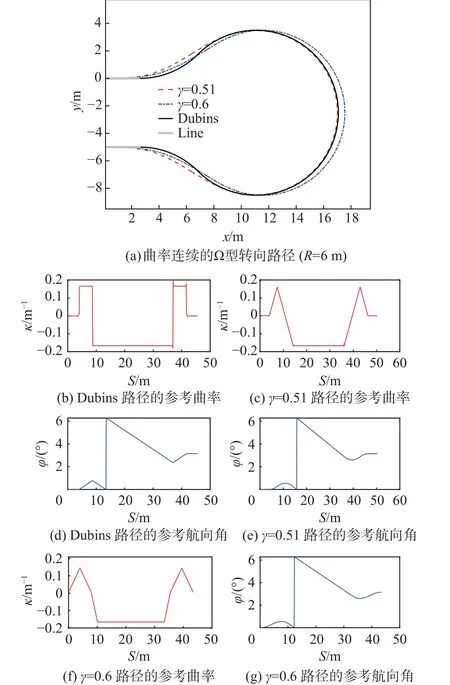
图11 曲率连续的Ω 型转向路径及曲率Fig. 11 Ω-shaped turning path with continuous curvature and curvature change of the path

1） 去掉双初等路径中的末端回旋线（即曲率κ减小为0 的部分）。

2） 保持前2 条回旋线不变。

3） 第3 条回旋线的曲率变化率不变，但是曲率κ的变化范围改为曲率从0 增大至曲率最大值κmax。

4） 变动γ值，使相切圆半径为Rmin，得到γdes。

分别计算得到γdes为0.51、0.6 的优化路径。原规划路径是Dubins 路径，由最小转向半径Rmin组成，如图11 所示。

优化Ω 型转向路径和U 型转向路径相比，所用回旋线的构造方法一样，但由于路径组成不同，Ω 型转向路径计算更复杂，考虑因素更多。

4 线性时变MPC 的轨迹跟踪仿真

4.1 控制系统

由于本文研究重点是对转向路径的优化，因此对转向路径的跟踪采用的车辆模型为单车模型，即只考虑牵引车在规划路径下的跟踪效果。提出一种基于模型预测控制器（model prediction control, MPC)的线性时变模型预测方法，作为跟踪控制方法，搭建控制器，控制系统框图如图12 所示。控制变量u为[v,ω]，状态变量ξ为[x,y,φ]，其中x和y分别表示牵引车的横向和纵向位置，φ表示牵引车的航向角，参考状态量为ξr，参考控制量为ur，参考速度表示为vr，参考角速度为ωr，参考航向角为φr。路径跟踪控制仿真中的牵引车车轴为3 m，车身宽为1.916 m，车体质量为1 412 kg，前轮最大转角为35°。

图12 控制系统框图Fig. 12 Block diagram of control system

4.2 轨迹跟踪仿真结果

4.2.1 优化前后U 型转向路径的轨迹跟踪效果对比

冲碾机的牵引车规划路径为R=6 m 的圆弧，所对比的优化路径分别为（6 m,0.5）、（6 m,0.7）、（7 m,0.7）和（8 m,0.5）。

基于MPC 的控制器参数：预测时域NP= 3，控制时域NC= 2，采用时间T= 0.1 s。权重Q取1 000，R按转向角的光滑程度而定。初始状态设置：初始转角δ0和角速度ω0，均设置为0。在转向过程中设定为匀速，v为2 m/s。约束条件的边界设置如下：

不同U 型转向路径车辆的横向跟踪误差如图13所示，车辆前轮转向角变化如图14 所示。

图13 不同U 型转向路径下横向跟踪误差Fig. 13 Lateral error of trajectory tracking for different U-shaped turning paths

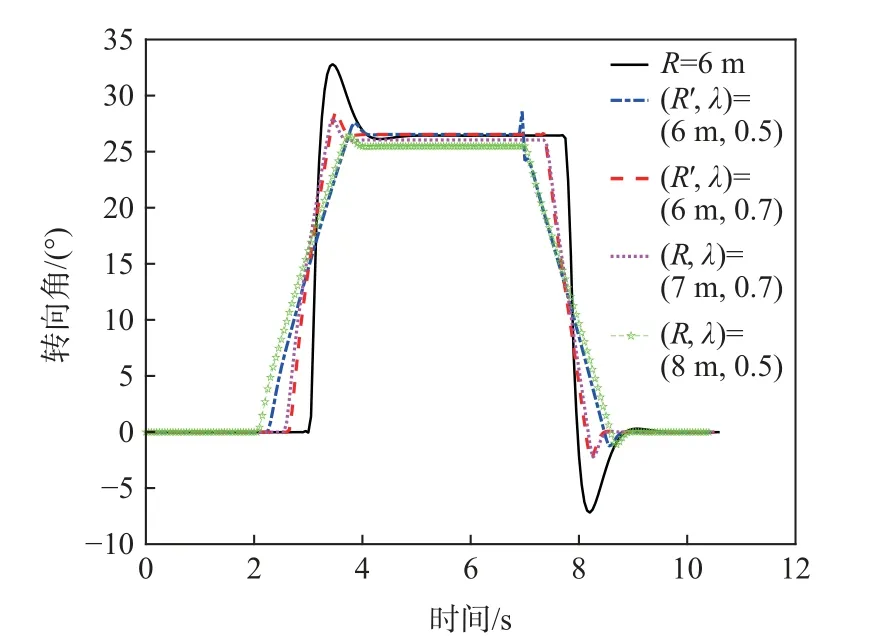
图14 不同U 型转向路径下轨迹跟踪的转向角Fig. 14 Steering angle of trajectory tracking for different U-shaped turning paths

从图13 看出，优化后路径误差降低了70%，从图14 看出，优化的路径转向角超调量小，转向角小。

4.2.2 优化前后Ω 型转向路径的轨迹跟踪效果对比

冲碾机的牵引车规划路径为Dubins（R=6 m）路径，所对比的优化路径分别为γ=0.51、γ=0.6 的双初等路径。基于MPC 的控制器参数如4.1 节设置。为优化后的Ω 型转向路径与原规划路径Dubins 的跟踪对比图分别如图15 和图16 所示。

图15 不同Ω 型转向路径下横向跟踪误差Fig. 15 Lateral error of trajectory tracking for different Ω-shaped turning paths

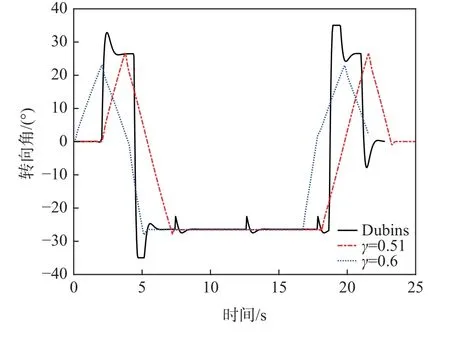
图16 不同Ω 型转向路径下轨迹跟踪转向角Fig. 16 Steering angle of trajectory tracking for different Ω-shaped turning paths

从图15 看出，优化的路径误差emax降低了80%，从图16 看出，优化路径转向角控制简单，无超调量。

5 结 论

本文提出了一种适用于冲碾机转向路径的优化方法，通过建立U 型转向路径和Ω 型转向路径主要有以下结论：

1） 基于广义初等曲线的U 型转向路径可利用不同含义的参数R来构造，通过2 种方法生成了4 组路径与原规划路径R=6 m 相近的曲线。从MPC 控制器的仿真结果看，优化后的路径横向跟踪误差降低了70%，转向角超调量减小，说明了方法的有效性。

2） 基于双初等曲线的Ω 型转向路径采用了优化手段，同时考虑曲率连续和Rmin约束，得到有效路径γ=0.51 和γ=0.6。从MPC 控制器的仿真结果看，优化后的路径横向跟踪误差降低了80%，转向角小，且控制简单，证明了路径优化方法的有效性。

基于广义初等曲线和双初等曲线所构造的冲碾机地头转向的最优U 型转向路径和Ω 型转向路径，丰富了冲碾机地头转向路径的研究，对于无人冲碾机的路径规划也有一定的借鉴意义。