受内压航空管道弯曲疲劳可靠性

沈兴铿， 王光强， 杨 婧， 员婉莹， 杨宏伟， 张屹尚， 戴 瑛， 贺鹏飞

（1.同济大学 航空航天与力学学院，上海 200092；2.中国航发商用航空发动机有限责任公司 研发中心，上海 200241；3.西北工业大学 航空学院，陕西 西安 710072）

航空器中有大量的管道，承担燃油、液压油、润滑油和空气等介质的输送，使飞行器实现如为发动机供油，起落架、襟翼和减速板的收放，润滑降温等工作。管道的失效破裂将会造成严重的飞行事故。随着飞机性能的不断提高，高压力、高功重比、大流量的要求，也导致管道的故障率呈逐年上升态势［1-2］，因此对管路的失效研究具有非常重要的意义。尽管管道的设计压力是系统工作压力的数倍，如液压管道的设计压力是系统工作压力的6～8倍［3］，在静载作用下有较大的安全裕度，但在管内流体的高压和外部振动共同作用下会引起疲劳破坏，这是管道故障的主要原因。相较于管内压力，外部振动通过卡箍作用于管道上的动应力会对管道反复作用，并在高应力区引起局部损伤及损伤累积，进而萌生裂纹，当疲劳裂纹长度达到临界值时，裂纹会失稳扩展，导致管道的疲劳破裂失效［4-7］，因此对受内压管道疲劳寿命的研究是非常必要的。

传统的管道疲劳寿命估计采用的是确定性模型，即在管道寿命分析过程中的参数如管材力学性能、振动载荷及内压、管道尺寸等参数都取确定的数值。但实际上由于加工、装配、测量等原因，上述参数均处于一个不确定的取值范围内，这些参数确定值的选择存在主观性。上述影响因素的随机性导致管道疲劳寿命本质上也是一个随机量。同时，在工程上常采用安全系数法以考虑不确定性因素对管道寿命的影响，但人为给定的安全系数若过大，会导致疲劳寿命的安全裕度过大［8］，因此，引入了基于概率的可靠性分析方法［9-10］进行管道疲劳寿命的预测。与确定性分析方法相比，基于概率的可靠性分析方法考虑了上述影响因素的随机性，从概率角度评估了管道寿命，从而可以最大程度上利用管道性能。

有效合理的可靠性分析方法是航空飞行器机结构疲劳寿命设计和控制的基础，一次二阶矩法［11］（first order second moment method， FOSM）、二次二阶 矩 法［12］（second order second moment method， SOSM）、响 应 面 法［13-14］（response surface method， RSM）以及Monte Carlo法［15-17］（MCM）等可靠性分析方法已被研究应用。FOSM和SOSM方法的主要思想是在均值点或设计点（失效域内联合概率密度最大的点）处采用线性超平面或者二次超曲面来近似实际功能函数，FOSM方法对于非线性极限状态方程的计算误差较大；利用二次曲面的SOSM可以提高非线性状态方程的计算精度，但由于SOSM需要求解功能函数对随机变量的二阶导数，因此计算很复杂，效率不高［18-19］。RSM法可通过拟合有限个样本点形成响应面函数，但当求解问题样本点数量大、状态函数高度非线性时，该方法显示出严重精度损失，并且，样本点的选择会影响拟合精度［20］。MCM具有扎实的理论基础且应用简单，但对于小概率事件，MCM需要进行很多次抽样，导致计算效率较低［21-22］。Kriging代理模型是目前研究较多的方法［23-27］，它作为一种估计方差最小的无偏估计模型，具有全局近似与局部随机误差相结合的优点，对非线性程度较高和局部响应突变问题具有良好的拟合效果，是适合用于本问题研究的方法。

本文引入基于概率的可靠性分析方法对受内压悬臂航空管道的弯曲疲劳寿命进行可靠性分析。通过管道三点弯曲试验结果，建立管道的Manson-Coffin疲劳寿命模型。以管道尺寸、材料参数和载荷为基本随机变量，使用结合Kriging代理模型法和Monte Carlo抽样法的主动学习可靠性分析方法（AK-MCS）［28-29］，在管道给定28 MPa内压、自由端5.06 mm纵向位移循环载荷工况条件下，进行管道弯曲疲劳寿命可靠性研究。本文通过与传统MCS方法计算效率的比较，证实了AK-MCS法可以在保证可靠性分析精度的同时大大降低计算量。另外，根据不同寿命阈值下的失效概率/可靠度的结果，得出管道的疲劳寿命-失效概率/可靠度曲线，为管道的工程应用提供了基于概率的寿命预测结果。

1 AK-MCS可靠性分析方法

AK-MCS可靠性分析方法［28-29］是Kriging代理模型法和基于Monte Carlo抽样法的主动学习可靠性分析方法，结合了Monte Carlo抽样法和Kriging代理模型法的共同优点，将传统Kriging代理模型的拟合对象从整个空间Rn缩减到仅含有nMC个样本的Monte Carlo样本池SMC上，并利用学习函数在样本池SMC中选择对Kriging代理模型拟合贡献最大的下一个评估点更新代理模型，直至建立Kriging代理模型对于样本池SMC有着较好的拟合，即自适应学习过程。以下对该方法作简单介绍。

1.1 Kriging代理模型

Kriging代理模型是一种估计方差最小的无偏估计模型，具有局部估计的特点。Kriging代理模型通过样本点（训练点）对模型进行训练以确定随机参数，然后利用建立的Kriging代理模型进行未知响应的预测。Kriging代理模型由参数线性回归模型和高斯随机过程组成：

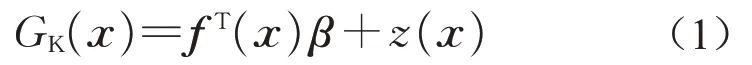
式中：f(x)=[f1(x)，f2(x)，…，fm(x)]T为回归基函数；β=[β1，β2，…，βm]T为回归系数；m为基函数的个数；z(x)为一个期望为0，方差为σ2的高斯随机过程，其协方差矩阵定义为

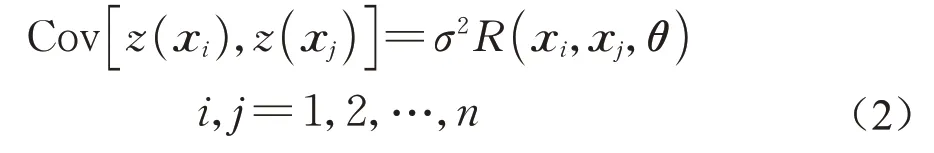
式中：R(xi，xj，θ)为两个任意的样本xi，xj之间的相关函数；n为训练样本的个数。相关函数R(xi，xj，θ)有多种形式，常用的是高斯型相关函数，其表达式为

式中：xik和xjk分别是样本向量xi和xj的第k个分量；θk(k=1，2，…，n)为相关参数，可以通过极大似然函数取最大值得到最优相关参数θ*［30］，即

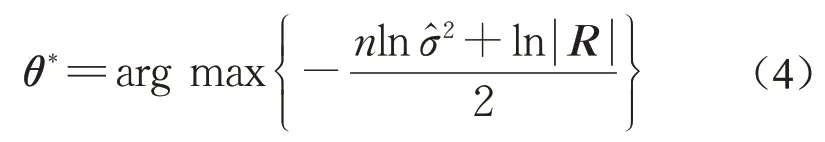
式中：过程方差估计值可以通过下式估计，即

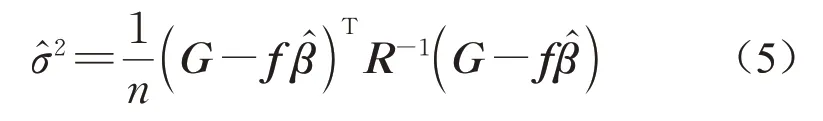
式中：G为训练样本的响应值向量；R为已知训练点的相关矩阵，Rij=R(xi，xj，θ)，(i，j=1，2，…，n）；β^为β的估计值，可以如下式估计，即

通过求解最优相关参数θ*可以得到拟合精度最高的Kriging代理模型。对于一个未知样本点x的响应估计值GK(x)服从高斯分布，即GK(x)～N(μGK(x)，(x))，其 均 值 和 方 差 计 算式为

式中：F为单位列向量；r(x)为训练点和预测点之间的相关函数，ri=R(x，xi，θ)，(i=1，2，…，n）；μGK和σ2GK可以使用MATLAB的Dace［31］工具箱进行求解，一般取预测均值μGK(x)作为Kriging响应GK(x)，而根据方差σ2GK的大小，可以判断Kriging代理模型的估计准确程度，这提供了更新Kriging代理模型的指标。

1.2 主动学习可靠性分析方法

结合Kriging代理模型的基于Monte Carlo抽样法的主动学习可靠性分析方法（AK-MCS）通过以下步骤实现：

（1）Monte Carlo样本池的生成以及初始训练的定义。在输入变量空间Rn根据随机变量的联合概率密度函数生成由nMC个样本点构成的Monte Carlo样本池并命名为SMC。从样本池SMC中随机选择N1个随机样本作为初始训练样本，并计算其相应的功能函数响应值G。

（2）Kriging代理模型的建立、预测以及失效概率估计。由选择的N1个样本及相应的响应值建立初始Kriging代理模型，并根据式（1）计算样本池SMC所有样本点的功能函数预测值GK。这一部分主要是在MATLAB的Dace工具箱中实现。然后根据GK的正负号得到失效概率的估计值，即

（3）确定性能函数计算的下一个评估点x*并判断学习停止条件。这一阶段需要计算样本池SMC中所有样本点的学习函数值，并由此确定下一个评估点x*。现有常用的学习函数有EFF函数［32］、U函数等［33］，本文中选择U函数进行下一个评估点x*的选择，其形式如下：

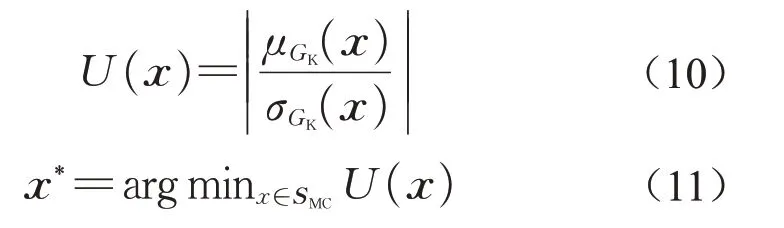
（4）通常，minU(x)≥2可以作为基于U学习函数的Kriging代理模型自适应更新过程收敛的终止条件。当该学习停止条件不满足时，使用下一个评估点x*更新Kriging代理模型。计算下一评估点x*的功能函数值，将这个样本点及其函数值加入之前的设计试验作为新的设计试验，并返回第（2）步重新构建Kriging代理模型。当学习停止条件满足时，继续执行第（5）步。

（5）失效概率变异系数的计算及Monte Carlo样本池的更新。根据式（12）计算失效概率估计值的变异系数，即

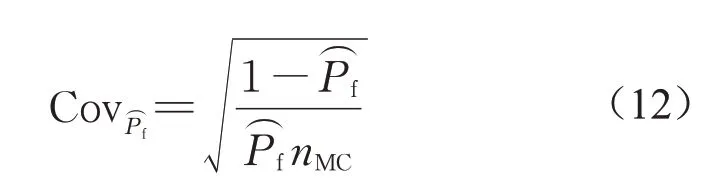
在自适应学习过程收敛后，通过失效概率的变异系数的大小判断当前失效概率的估计是否稳健。一般变异系数低于5%可以认为样本池SMC已经足够大且能够稳健地估计失效概率。若变异系数大于5%，则增加Monte Carlo样本池的数量以提高估计值的稳健性，即扩充样本池SMC并返回第（2）步，使用之前建立的Kriging代理模型重新计算得到所有预测值G′K，并进行自适应学习，直至满足收敛条件。

（6）结束AK-MCS方法。当第（5）步计算得到的失效概率估计值的变异系数小于5%时，输出当前计算的失效概率及失效概率估计值的变异系数，完成可靠性评估。

2 管道弯曲疲劳寿命预测

由于航空飞行器中的管道所受绝大多数为弯曲振动，因此本文采用三点弯曲试验方法来确定管道的疲劳寿命。

2.1 管道的三点弯曲疲劳试验

试验参考金属弯曲规范和弯曲疲劳规范［34-37］，考虑实际卡箍的约束形式，设计夹具如图1所示，实现对称循环疲劳加载，即应力比R= -1。

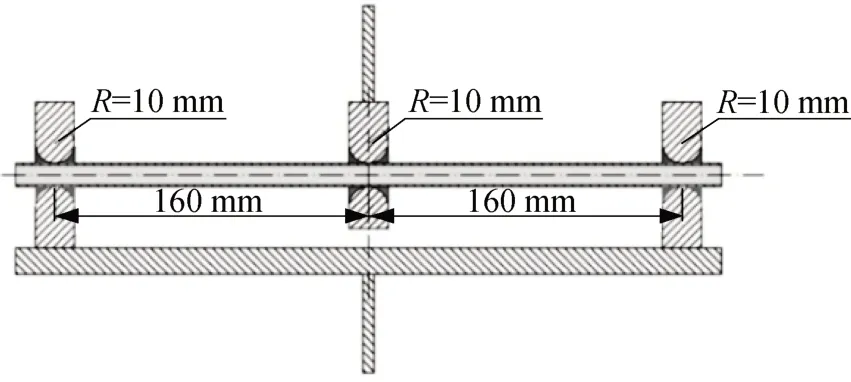
图1 三点弯曲疲劳试验夹具示意图Fig.1 Sketch of fixture for three-point bending fatigue test

在管道的三点弯曲疲劳加载试验中，管道外径12 mm，壁厚1 mm，长度360 mm 。疲劳试验机型号为MTS-858/2.5T，加载范围±25 kN，加载行程 100 mm，加载频率范围 0～25 Hz。试验选取 5 种位移幅值：2.33、2.67、3.00、3.33和4.00 mm。每种位移幅值保证 3 个以上的有效试验数据。试验在室温下进行，加载频率为18 Hz，数据采样频率为加载频率的10倍。图2为试验照片。

图2 三点弯曲疲劳试验照片Fig.2 Photo of three-point bending fatigue test

2.2 疲劳试验数据统计分析

疲劳寿命存在分散性大的问题，主要源自不同样本之间的差异，如材料属性、表面粗糙度和内部缺陷等，因此，需要引入统计理论分析获得应变Δε与疲劳寿命Nf的Δε-Nf曲线。

疲劳试验数据的Δε-Nf关系通过线性回归模型进行统计分析［38］。该方法假设疲劳寿命服从对数正态分布，并且对数寿命的方差在整个测试范围内是恒定的。在双对数坐标中，Manson-Coffin疲劳寿命模型可以由lg和lg(2Nf)之间的线性模型进行描述，其中Δεe为弹性应变，Δεp为塑性应变，线性关系如图3和图4所示，图中同时给出了线性模型具有95%置信度的置信带。由此可以得到基于疲劳试验数据线性回归分析的Manson-Coffin疲劳寿命模型为

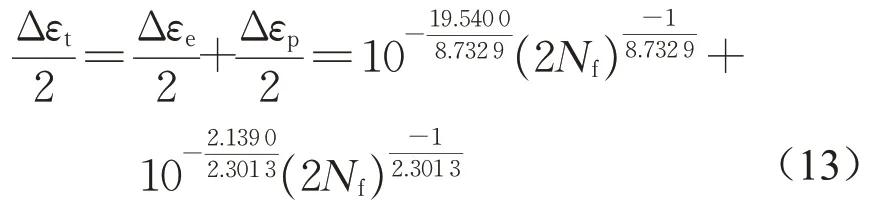
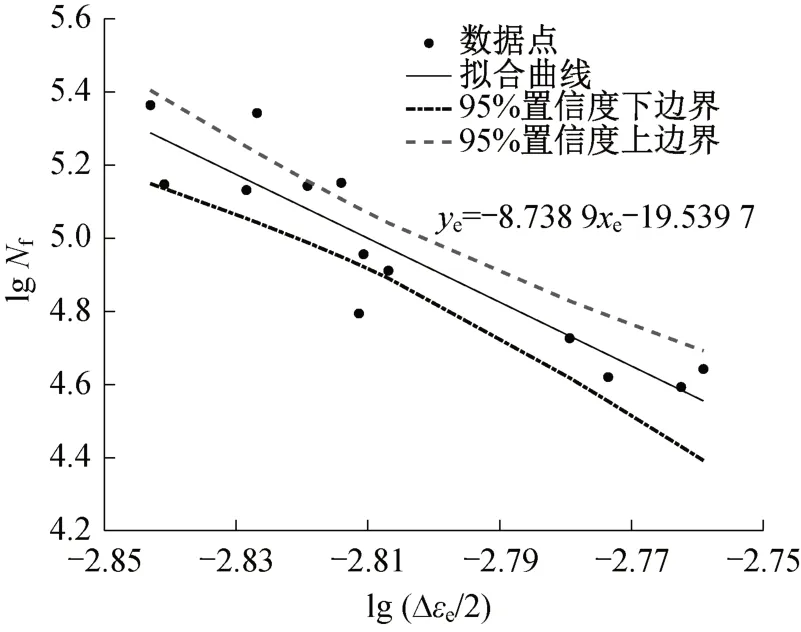
图3 lg Nf与lg之间的拟合关系Fig.3 Fitting relation between lg Nf and lg

图4 lg Nf与lg之间的拟合关系Fig.4 Fitting relation between lg Nf and lg

3 管道弯曲疲劳可靠性分析

以悬臂航空管道在内压28 MPa，自由端5.06 mm纵向位移循环载荷的工况为例［39］，进行弯曲疲劳寿命可靠性分析。受内压悬臂管道弯曲疲劳试验示意图如图5所示［39］。该试验结构由直管一端的螺母与阀块之间的螺纹连接，构成悬臂梁的固定端。油泵产生的油液由软管通入阀体为悬臂直管提供固定的内部压强。管道另一端通过堵头密封，防止油液外泄，且在该端通过卡箍将管道与激振器连接。通过激振器的高频上下振动，对管道施加对称的循环位移载荷。

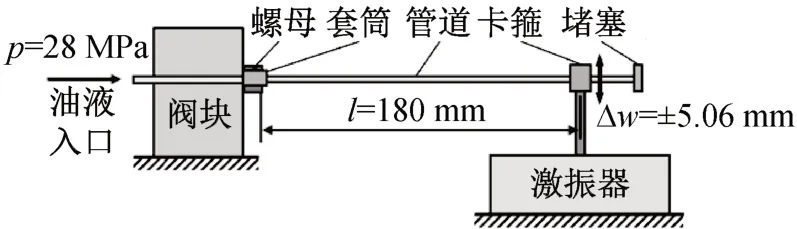
图5 受内压悬臂管道弯曲疲劳试验示意图Fig.5 Sketch of bending fatigue test of cantilever pipeline under internal pressure

3.1 随机变量的确定

基本随机变量是结构可靠度分析的重要输入变量，其不确定性导致了结构输出响应的不确定性。在受内压管道弯曲疲劳可靠性分析中，基本变量有：几何尺寸、材料参数和工作载荷。这些变量都具有随机性，增加了基本变量选取的复杂性。本文选取的随机变量为：管道的几何尺寸考虑管道半径r和管道厚度t；工作载荷包括位移载荷w和管道内压p；材料参数包括管材的弹性模量Ep和泊松比μp以及连接件的弹性模量Ec和泊松比μc，以上随机变量及相应的分布模型如表1所示。

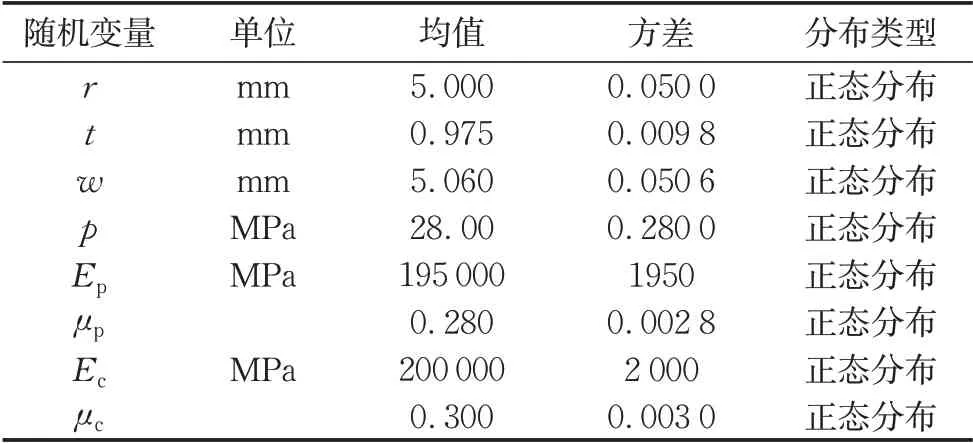
表1 基本随机变量及相应的分布模型Tab.1 Basic random variables and corresponding distribution models

3.2 结构应力分析

本文采用ABAQUS有限元软件进行确定性应力应变分析。根据管道的对称性，为了简化计算，取其1/2的几何模型建立含13 808个单元，19 677个节点的有限元模型，如图6所示。模型采用8节点六面体C3D8R单元进行网格划分，在靠近套筒位置对直管模型进行网格加密。整个航空管道内壁施加28 MPa内压，另外在加载端施加幅值为5.06 mm的循环弯曲位移载荷。计算悬臂管道的弯曲应力应变，并由式（1）计算相应的疲劳寿命。在确定性分析中，各参数均选择表1所示的随机变量的均值进行分析计算。

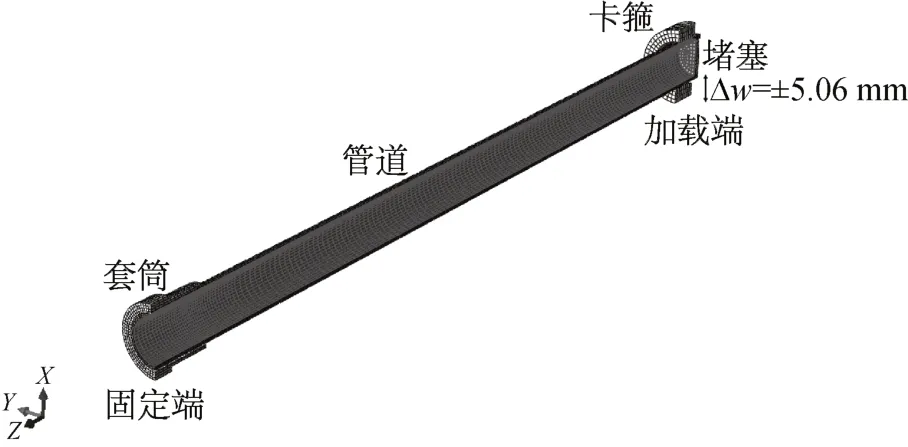
图6 受内压管道有限元模型Fig.6 FEM model of internal pressured pipeline

确定性分析的节点最大主应变和主应力结果如图7和图8所示。由图7和图8可知，管道的最大主应力和主应变出现在固定端一侧的管道根部，即此位置的疲劳寿命最低。由图7可得，此位置的半应变幅Δεt/2=3.290 8×10-3，由公式（1）计算得到Nf=12 031个周期，该寿命与Yang等［39］试验测得的受内压管道疲劳平均寿命Nf=12 806非常接近，验证了该寿命模型的准确性和有效性。同时，记录单次有限元计算时间为47 s，用以后续的AK-MCS法和MCS法的计算效率对比。

图7 悬臂管主应变分布云图和最大主应变位置局部放大图Fig.7 Nodal principal strain distribution contour of cantilever pipeline and local amplified view of maximum principal strain position

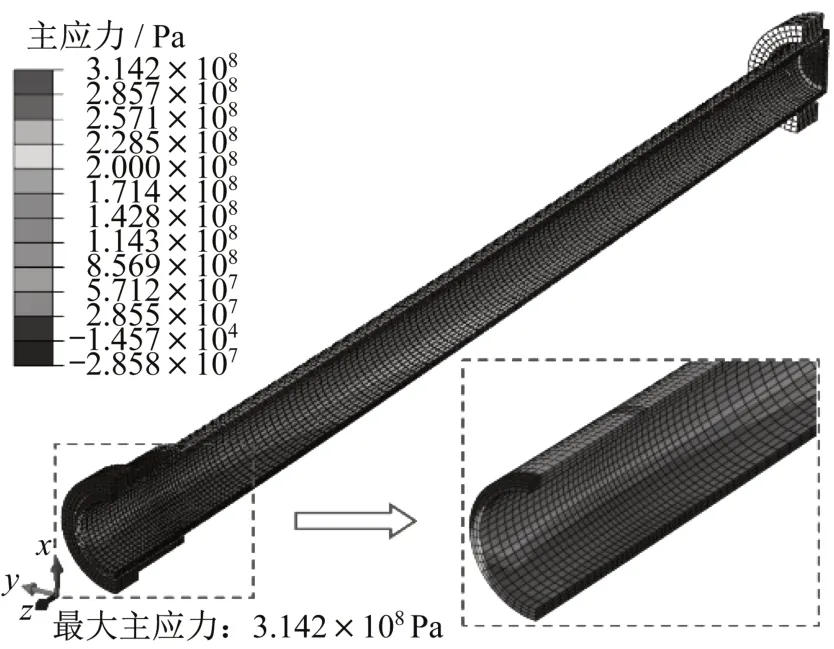
图8 悬臂管主应力分布云图和最大主应力位置局部放大图Fig.8 Nodal principal stress distribution contour of cantilever pipeline and local amplified view of maximum principal stress position

3.3 受内压管道疲劳可靠性分析及结果

根据确定性分析结果，受内压管道的最大应力应变位置出现在固定端一侧的管道根部，该位置的疲劳寿命即为管道的寿命。本文以受内压悬臂管道在固定端一侧的管道根部位置的疲劳寿命小于等于规定的寿命阈值N*f作为失效事件F，以该部位的疲劳寿命大于N*f作为安全事件S。由此可以定义受内压管道疲劳寿命可靠性分析的极限状态函数为

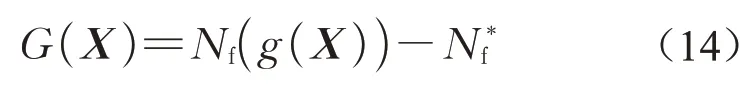
式中：Nf(·)为疲劳寿命函数；g(·)为结构响应计算函数，描述输入随机变量与输出的应力应变之间的关系；N*f为寿命阈值，不同的寿命阈值对应不同的失效概率Pf。相应的管道疲劳的失效概率和相应的可靠概率定义如下：

式中：P｛｝表示概率算子。

本文采用AK-MCS分析方法根据2.2节中的步骤对受内压管道弯曲疲劳的可靠性进行分析。在步骤（1）中，由表1中随机变量的联合概率密度函数生成nMC=50 000个Monte Carlo样本点，并从中随机选择N1=30个随机样本作为初始训练样本s（s1，s2，…，s30）。在步骤（2）中，通过ABAQUS软件计算得到训练样本对应的σm和 Δεt，根据式（13）计算相应的疲劳寿命Nf，结合式（14）计算寿命阈值N*f对应的功能函数G值。

为了验证AK-MCS法的有效性，本文同时采用Monte Carlo法进行结果比对。由于Monte Carlo法在求解小概率事件时存在所需样本点过大的问题，故针对疲劳寿命阈值为9 500个周期的小失效概率事件进行效率对比。两种方法的效率对比结果见表2。对于Monte Carlo法，进行50 000次随机抽样并计算其功能函数的值。根据4.2节的结构应力分析可知，每次有限元计算时间为47 s，所以共需要花费652.78 h，计算量很大。而相应使用代理模型的方法，共需要调用141次有限元计算，其中包括30次建立初始Kriging模型和111次修正模型，共花费1.84 h，降低了99.72%的有限元计算时间，而调用Kriging代理模型计算样本点响应的时间相较于有限元计算时间可以忽略不计。并且两种方法得到的失效概率基本上可以认为是相同的。故AK-MCS方法对于失效概率求解有着很好的准确性和高效性。

表2 MCS法和AK-MCS法计算效率对比Tab.2 Comparison of computation efficiency between MCS and AK-MCS

取不同的寿命阈值N*f，可以得到相应的失效概率和可靠度，结果如表3所示。

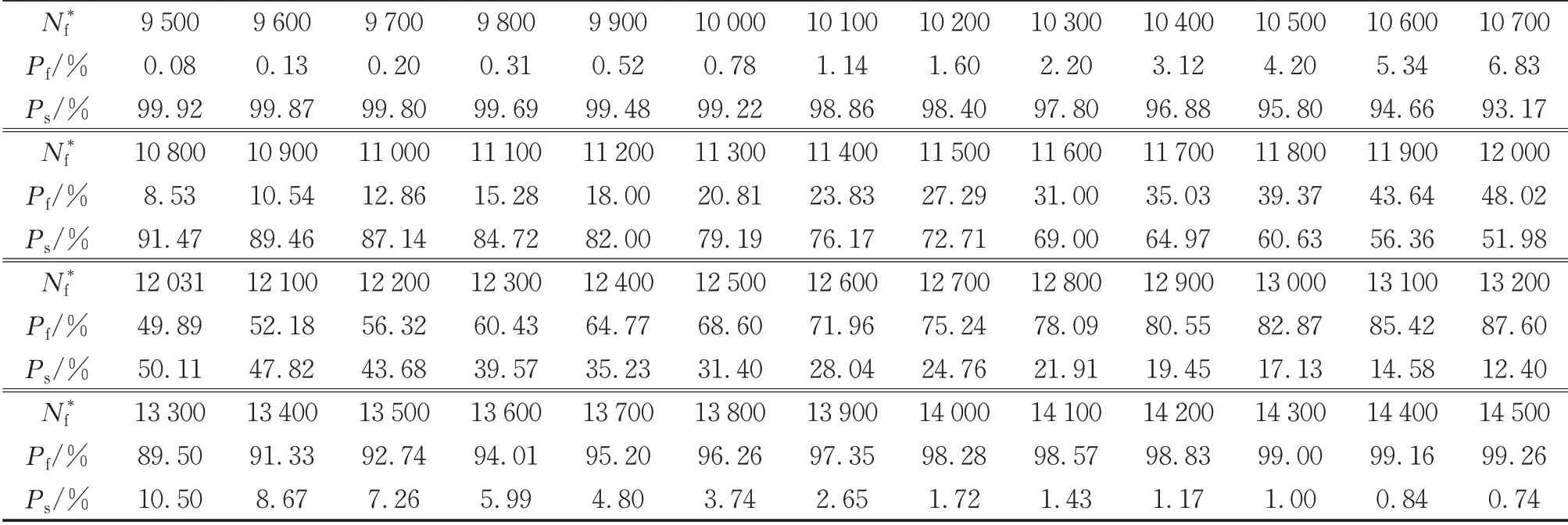
表3 受内压管道疲劳可靠性分析结果Tab.3 Reliability analysis results of fatigue life of pressure pipeline

疲劳寿命-失效概率/可靠度曲线如图9所示，该曲线可以为内压管道的工程应用提供基于概率的寿命预测结果。

由表3和图9可知，受内压管道的疲劳寿命小于10 000个周期的概率在1%以内，而当疲劳寿命达到14 500个周期时，受内压管道失效的概率将超过99%。同时，确定性分析寿命Nf对应的可靠度为49.89%。

根据图9中的疲劳寿命-失效概率曲线，可以得到样本总数为50 000的情况下，受内压管道疲劳寿命频数直方图，如图10所示。由图10曲线可知，受内压管道疲劳寿命分布总体上为正态分布形式，曲线峰值出现于疲劳寿命均值12 035处。受内压管道的疲劳寿命分布可以通过一定量的疲劳试验样本均值和方差进行近似估计，该结论对受内压管道的初步工程设计具有指导意义。

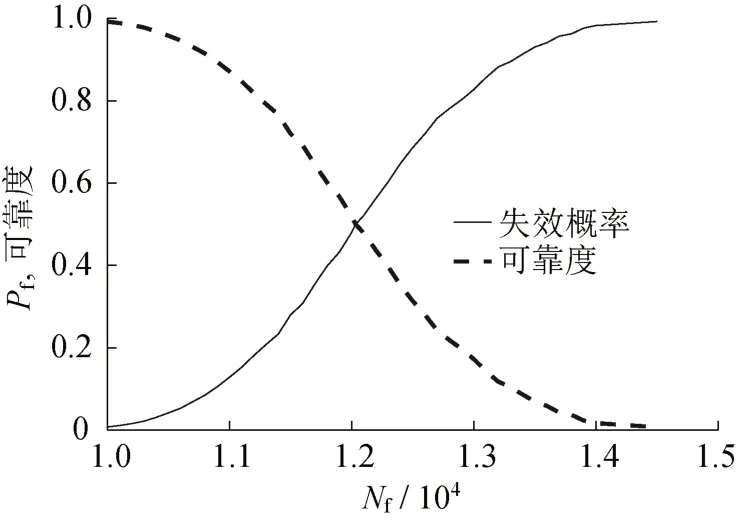
图9 疲劳寿命-失效概率/可靠度曲线Fig.9 Fatigue life-failure probability/reliability curve

图10 受内压管道疲劳寿命频数直方图Fig.10 Histogram of fatigue life frequency of pipeline under internal pressure

4 结论

在高流体内压和外部随机振动共同作用下的疲劳失效是飞行器管道的主要破坏模式之一，因此相应的疲劳寿命的研究是非常必要的。本文首先针对航空管道进行无内压三点弯曲疲劳试验，试验结果表明，管道的疲劳寿命存在着很大的分散性，这种分散性来自于不同样本之间的差异，如材料属性、表面粗糙度和内部缺陷等。故通过线性回归模型进行统计分析，建立基于统计理论的受内压管道Manson-Coffin疲劳寿命模型；其次，研究受内压管道在给定工况（28 MPa内压，自由端5.06 mm纵向位移循环载荷）的疲劳寿命，以管道尺寸、作用载荷以及管材材料性能参数为基本随机变量；最后，采用AKMCS方法进行受内压管道疲劳寿命可靠性分析。分析得到以下结论：

（1）由AK-MCS方法得到受内压管道的弯曲疲劳寿命-失效概率/可靠度曲线，该曲线为受内压管道的工程应用提供了基于概率的寿命预测值。根据该曲线得到样本总数为50 000下的受内压管道疲劳寿命的频数直方图，疲劳寿命总体上呈正态分布。

（2）在管道弯曲疲劳寿命可靠性分析过程中，通过确定性分析计算得到各变量取均值情况下的疲劳寿命为Nf=12 031，该寿命与YANG等人试验测得的受内压管道疲劳平均寿命Nf=12 806非常接近，从而验证了Manson-Coffin疲劳寿命模型的有效性和准确性。同时，确定性分析寿命Nf对应的可靠性为49.89%，从而验证了AK-MCS法可靠性分析方法的有效性和准确性。

（3）通过AK-MCS方法与传统的MCS方法计算失效效率的对比发现，对于寿命阈值取9 500个周期的小概率失效事件，AK-MCS方法将调用有限元计算次数从传统的MCS方法需要调用的50 000次降低到141次，降低了99.72%的有限元计算时间，同时保证计算所得的失效概率几乎相等。从而证明AK-MCS可以在保证可靠性分析精度的同时大大降低计算量。

作者贡献声明：

沈兴铿：试验实施，理论分析和计算，论文撰写。

王光强：试验方法指导。

杨 婧：试验指导。

员婉莹：可靠性分析理论指导。

杨宏伟：试验设计和实施。

张屹尚：试验设计和指导。

戴 瑛：论文总体指导和修改。

贺鹏飞：方法和试验指导。